Судавная О.И., Фролов С.В Типовые расчеты по высшей математике. Методические указания и задачи для студентов вечернего отделения. I семестр
Подождите немного. Документ загружается.


1
s
2
s
12
A
A
→
=
213
113 2361
011
0
−
=− − + − =
−
.
Из равенства нулю смешанного произведения векторов следует, что они
компланарны, значит, прямые лежат в одной плоскости. Поскольку
координаты направляющих векторов не пропорциональны, то прямые не
параллельны. Следовательно, прямые (1) и (2) пересекаются, что и
требовалось доказать.
2) Найдем уравнение плоскости, проходящей через две пересекающие
прямые (1) и (2). Для этого введем текущую точку M(x; y; z) искомой
плоскости и построим вектор
1
A
M
→
= {x–1; y–1; z}. Учитывая
компланарность векторов
1
A
M
→
,
1
s
и
2
s
, получим
1
A
M
→
1
s
2
s
= 0, или
11
213
113
xyz−−
0
=
−
. Вычислим определитель в левой части уравнения:
11
13 23 21
213(1) (1)
13 13 1 1
113
xyz
xyz
−−
=− −− + =
−
−
−
(3 3)( 1) (6 3)( 1) ( 2 1) 6 6 3 3 3 6 3 3 3
xy
zx
y
zx
y
z=+ −−− −+−− = −− +− = − −−
Таким образом, уравнение искомой плоскости:
63330
x
yz
−
−−=
, или, что
то же самое,
210
xy
z
−
−−=
Ответ:
210
x
yz
−
−−=
.
Замечания. 1) Для доказательства параллельности двух прямых,
уравнения которых записаны в канонической форме, достаточно доказать,
что их направляющие векторы коллинеарны, т. е. координаты направляющих
векторов пропорциональны.
2) Для доказательства того, что прямые, уравнения которых записаны в
канонической форме, скрещиваются, достаточно доказать, что их
направляющие векторы и вектор, соединяющий две точки, лежащие на
прямых, некомпланарны, т. е. смешанное произведение этих векторов не
равно нулю. Для этого нужно составить определитель из координат этих
векторов и показать, что он отличен от нуля.
Пример 6. Составьте канонические и параметрические уравнения
прямой, заданной пересечением двух плоскостей .
23
23
xy z
xyz
+− =
⎧
⎨
++=−
⎩
0
10
Решение. Выберем произвольную точку, лежащую на прямой, т. е. точку,
координаты x
0
, y
0
, z
0
которой удовлетворяют уравнениям обеих плоскостей.
Для этого одной из координат придадим произвольное значение, а остальные
найдем, подставив это произвольное значение в систему, составленную из
уравнений плоскостей. Пусть, z
0
= 0. Тогда x
0
, и y
0
найдем из системы
20
23
xy
xy
+=
⎧
⎨
+=−
⎩
. Решив систему, получим x
0
= 1, y
0
= – 2. Таким образом,
прямая проходит через точку М
0
(1; – 2; 0).
В качестве направляющего вектора прямой можно взять любой вектор,
перпендикулярный как первой, так и второй плоскости, например, векторное
произведение нормальных векторов данных плоскостей.
Найдем векторное произведение нормальных векторов и
плоскостей:
1
{2;1; 3}n =−
2
{1; 2 ; 1}n =
12
13 23 21
21 3 7 5 3
21 11 12
12 1
ijk
nn i j k i j k
−−
×= −= − + =−+
.
Полученный вектор может служить направляющим вектором прямой:
{7; 5; 3}
s
=−
. Подставив координаты точки М
0
и направляющего вектора в
канонические уравнения прямой
000
x
xyyzz
klm
−
−−
==
, будем иметь
12
753
x
y−+
==
−
z
. Приравняв каждое отношение к t и выразив x, y, z через t,
получим параметрические уравнения прямой:
71
52
3
xt
yt
zt
=
+
⎧
⎪
=
−−
⎨
⎪
=
⎩
.
Ответ:
12
753
x
yz+
==
−
71
52
3
xt
yt
zt
;
=
+
⎧
⎪
−
=
−−
⎪
=
⎩
⎨
.
Пример 7. Геометрическое тело ограничено поверхностями
x
2
+ y
2
+ 4z
2
= 25 и x
2
+ y
2
– z
2
= 5 и содержит точку О(0;0;0).
1) Изобразите сечение тела координатной плоскостью Oyz. Определите
вид кривых, ограничивающих сечение. Найдите координаты точек их
пересечения.
2) Определите вид поверхностей, ограничивающих тело. Сделайте его
схематический рисунок.
11
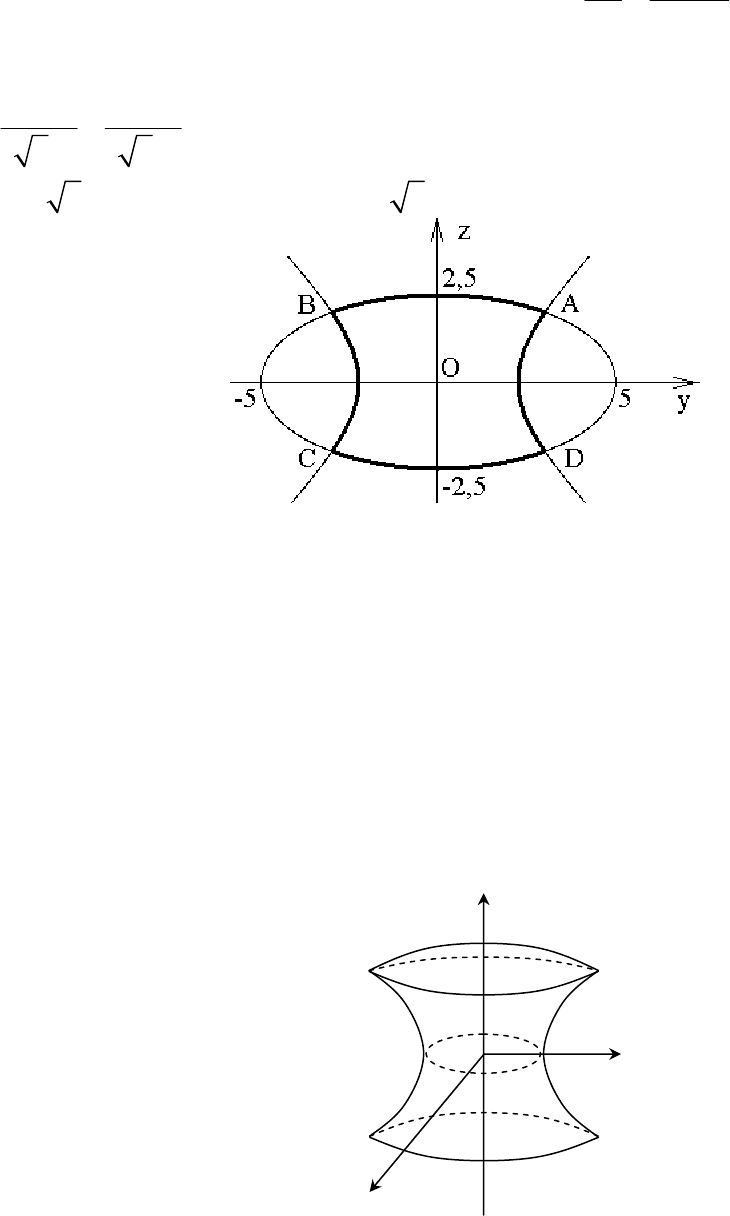
Решение. 1) Для всех точек плоскости Oyz справедливо условие x = 0.
Подставив это значение в уравнения поверхностей, получим уравнения
кривых, ограничивающих сечение: y
2
+ 4z
2
= 25 и y
2
– z
2
= 5.
Разделив первое уравнение на 25, получим
22
22
1
5 (2,5)
у z
+
= – уравнение
эллипса с полуосями a = 5, b = 2,5. Разделив второе уравнение на 5, получим
22
22
1
(5) (5)
у z
−= – уравнение гиперболы с действительной полуосью
5a = и мнимой полуосью 5b = . Эти кривые изображены на рис. 1а.
Рис. 1а
Для нахождения координат точек пересечения кривых составим и решим
систему двух уравнений с двумя неизвестными:
22 2 2
22 2 2
425545 9
;
20 4
y y
z
⎧
= =
⎪
⎨
= =
⎪
⎩
;
55
yz
yz z
⎧⎧
+=
⎪⎪
⎨⎨
−=
⎪⎪
⎩⎩
. Система имеет 4 решения:
(3; 2),(– 3; 2), (– 3; – 2), (3; – 2). Таким образом, кривые пересекаются в
четырех точках A(3;2), B(– 3;2), C(– 3;– 2), D(3; – 2). Согласно условию,
искомое сечение содержит точку О(0;0). На рис 1а оно представлено фигурой
ABCD .
2) Тело, ограниченное указанными поверхностями получим, если будем
вращать фигуру ABCD вокруг оси Oz.
z
y
x
12

Рис. 1б
Данное тело схематически изображено на рис 1б. Оно ограничено
эллипсоидом
22 2
22 2
22 2
425
552,5
xy z
xy z++ =⇔ + + =1
и однополостным
гиперболоидом
222
222
222
51
(5) (5) (5)
xyz
xyz+−=⇔ + − =.
Пример 8. Геометрическое тело ограничено поверхностями
2z
= x
2
+ y
2
и x + z = 4.
1) Изобразите сечение тела координатной плоскостью Oxz. Определите
вид кривых, ограничивающих сечение. Найдите координаты точек их
пересечения.
2) Определите вид поверхностей, ограничивающих тело. Сделайте его
схематический рисунок.
Решение. 1) Для всех точек плоскости Oxz справедливо условие y = 0.
Подставив это условие в уравнения поверхностей, получим уравнения линий,
ограничивающих сечение: 2z
= x
2
и x + z = 4.
Первое уравнение задает параболу, а второе – прямую. Для нахождения
координат их точек пересечения составим и решим систему двух уравнений с
двумя неизвестными:
222
24
280
;;
28
4
xx
x
zz
x
⎧
22(4)
;;
44
zx x x x
xz z x z
⎧
⎧
⎧
=
=−
⎧
+−=
⎨⎨
=−=
⎪⎪ ⎪
⎨⎨ ⎨
=
=
=−
⎩
⎪⎩
.
+= =−
⎪
⎪
⎩
⎩
⎩
Парабола и прямая пересекаются в точках K(2; 2) L( – 2; 8). Искомое
сечение, представляющее собой фигуру OKL, изображено на рис. 2а.
Рис. 2а Рис. 2б
z
y
x
2) Тело ограничено следующими поверхностями:
13

22
22
2
22
xy
zx y z=+⇔= + – эллиптическим параболоидом и x + z = 4 –
плоскостью, параллельной оси Oy. Искомое тело схематически изображено
на рис. 2б.
14
Расчетные задания
I. С помощью метода Гаусса найдите решения системы линейных
уравнений или докажите ее несовместность.
1. 2.
123
123
123
123
0
23
23 2
20
xxx
xx x
xx x
xxx
+−=
⎧
⎪
−+=
⎪
⎨
−+−=
⎪
⎪
−+ − =
⎩
2−
2
12 3
123
123
12 3
23
32 2
0
20
xx x
xxx
xxx
xx x
−
++ =
⎧
⎪
−
−=
⎪
⎨
−
−
+=
⎪
⎪
−
−=
⎩
3.
⎨
4.
1234
12 3 4
1234
12 34
2
21
224
022
xxxx
xx x x
xxxx
xx xx
+−+=
⎧
⎪
−++−=
⎪
−+ −+=
⎪
⎪
+− +=
⎩
123
234
134
12 4
0
5
6
1
xx x
xxx
xxx
xx x
+
+=
⎧
⎪
+
+=
⎪
⎨
+
+=
⎪
⎪
+
+=
⎩
9
0
1
5. 6.
1234
1234
1234
1
22 2
23
xxxx
xxxx
xxxx
+++=
⎧
⎪
−++=
⎨
⎪
+++=
⎩
1234
12 34
123
123 4
22
23
1
20
xxxx
xx xx
xx x
xx x x
+
++=
⎧
⎪
+
+−=
⎪
⎨
−
+
+=
⎪
⎪
−
−−=
⎩
7. 8.
123 4
1234
12
1234
0
23
34
222
xx x x
xxx x
xx
xxxx
++ −=
⎧
⎪
+−+=
⎪
⎨
+=
1
1
1
−
⎪
⎪
+−+=−
⎩
123
12 3
12 3
12 3
20
21
22
30
xxx
xx x
xx x
xx x
−
+
−=
⎧
⎪
+
+=
⎪
⎨
−
+− =−
⎪
⎪
−
+=
⎩
1
−
1
9
0
9. 10.
123
12 3
12 3
123
21
22
20
2
xxx
xx x
xx x
xxx
++ =
⎧
⎪
++ =
⎪
⎨
−+ − =
⎪
⎪
−+ =
⎩
12 34
123 4
1234
24
23 2
236
xx xx
xxx x
xxxx
+
−+
⎧
⎪
=
+
+− =
⎨
⎪
−
+−=
⎩
11.
⎪
⎨
12.
1234
1234
123 4
21
0
221
xxxx
xx xx
xx x x
+−+=
⎧
−− −− =
⎪
++− =−
⎩
1234
1234
12 34
12 3 4
23
3
23
8
22
1
0
xxxx
xxxx
xx xx
xx x x
+− +
=
⎧
⎪
++−
=
⎪
⎨
−+ +
=
−
⎪
⎪
−+ − −
=
⎩
15
13.
1234
12 3 4
12 34
12 3
2
0
2
1
2
2
2
2
xxxx
xx x x
xx xx
xx x
+−−
=
⎧
⎪
−+ +−
=
⎪
⎨
−+ −
=
⎪
⎪
++
=
⎩
14.
1234
1234
1234
1 234
2
4
2
4
xxxx
xx xx
xxxx
xxxx
++−
=
⎧
⎪
−+ −+
=−
⎪
⎨
−++
=−
⎪
⎪
+++
=
⎩
15.
123 4
12 3 4
134
23
3
2
2
22
5
23
1
xx x x
xx x x
xxx
xx
−+ −
=
−
⎧
⎪
−− + +
=
⎪
⎨
−−
=
−
⎪
⎪
−
=
⎩
16.
1234
12 3 4
1234
32
1
22 23
xxxx
xx x x
xx xx
5
0
+
−+
⎧
⎪
=
−
−+−
⎨
⎪
=
−
++=
⎩
17. 18.
123
12 3
123
13
22
22
3
2
xxx
xx x
xx x
xx
−+=−
⎧
⎪
−++ =
⎪
⎨
−−+=−
⎪
⎪
−=−
⎩
9
1234
12 3 4
123
1234
223
6
23
6
0
2
4
xxxx
xx x x
xxx
xxxx
−+−
=
⎧
⎪
−+−+
=
−
⎪
⎨
+−
=
⎪
⎪
−+−
=
⎩
19.
⎪
⎨
20.
123 4
12 3 4
123 4
21
22 0
24
xxx x
xx x x
xx x x
+−+ =
⎧
−−+ −=
⎪
−+ −− =
⎩
12 34
12 3 4
1234
134
23
6
2
3
22
0
32
0
xx xx
xx x x
xx xx
xxx
++ −
=
⎧
⎪
−−+
=
⎪
⎨
−+ + +
=
⎪
⎪
+−
=
⎩
2
3
3
21. 22.
123
12 3
12 3
13
25 3
4
23
27
xxx
xx x
xx x
xx
−− =
⎧
⎪
−+ +=−
⎪
⎨
+− =−
⎪
⎪
−=−
⎩
12 34
1234
12 34
1
22
20
xx xx
xxxx
xx xx
−
++−
⎧
⎪
=
−
++=
⎨
⎪
−
+−=
⎩
23.
123 4
1234
1234
12 4
2
0
22
1
3
2
22
0
xxx x
xx xx
xxxx
xx x
−++
=
⎧
⎪
−+ − −
=
⎪
⎨
−++
=
⎪
⎪
−+
=
⎩
24.
1234
12
1234
1234
222
1
34
1
0
23
1
xxxx
xx
xx xx
xxx x
+−+
=
−
⎧
⎪
+
=
−
⎪
⎨
++−
=
⎪
⎪
+−+
=
−
⎩
25.
12 34
134
23
12 3 4
2
2
22
5
23
1
3
xx xx
xxx
xx
xx x x
+− −
=
−
⎧
⎪
−−
=
−
⎪
⎨
−
=
⎪
⎪
−+ − +
=
⎩
26.
1234
1234
1234
1234
1
2223
0
32
5
24 32
4
xxxx
xxxx
xxxx
xx x x
+−+
=
−
⎧
⎪
−++
=
⎪
⎨
+− +
=
⎪
⎪
−− +−
=
−
⎩
16
II. Вектор
{
}
;;dxyz=
удовлетворяет условиям а), б) и в).
1) Составьте систему линейных уравнений, связывающих координаты
вектора
d
.
2) Решите эту систему двумя способами: по формулам Крамера и с
помощью обратной матрицы.
3) На векторах
,,abc
построена треугольная пирамида. Найдите ее
высоту, опущенную на грань, проходящую через векторы
иab
.
1. а) Вектор
d
ортогонален вектору
{
}
2; 1; 1a
=
−−
, б) скалярное
произведение вектора
d
и вектора
{
}
0;1; 3b
=
−
равно –11, в) проекция
вектора
d
на вектор
{
}
2; 2; 1c =− −
равна – 8/3.
2. а) Скалярное произведение вектора
d
и вектора
{
}
3; 2; 6a
=
−
равно 4, б)
проекция вектора
d
на вектор
{
}
1; 0; 2b =
равна 0,2 5 , в) скалярное
произведение вектора
d
и вектора
{
}
0; 2;1c
=
равно –2.
3. а) Скалярное произведение вектора
d
и вектора
{
}
1;1; 2a =
равно 2, б)
скалярное произведение вектора
d
и вектора
{
}
1; 1; 0b =−
равно 3, в)
проекция вектора
d
на вектор
{
}
2;1; 2c
=
−−
равна – 2.
4. а) Вектор
d
ортогонален вектору
{
}
2;3;1a
=
, б) проекция вектора
d
на
вектор
{
}
0; 1;1b =−
равна 0,5 2 , в) скалярное произведение вектора
d
и
вектора
{
}
2; 1; 6c =−
равно 6.
5. а) Вектор
d
ортогонален вектору
{
}
3; 2; 1a
=
−−
, б) проекция вектора
d
на вектор
{
}
1;1;1
равна
b =
3/3, в) скалярное произведение вектора
d
и
вектора
{
}
0;3; 2c =
равно 1.
6. а) Проекция вектора
d
на вектор
{
}
1; 3; 0a
=
равна 0,5 10 , б) скалярное
произведение вектора
d
и вектора
{
}
3;1; 2b =−
равно 10, в) проекция
вектора
d
на вектор
{
}
1;1; 1c =−
равна 23.
17

7. а) Проекция вектора
d
на вектор
{
}
1;1; 1a
=
−
равна 3 , б) вектор
d
ортогонален вектору
{
}
1; 1;1b =−
, в) скалярное произведение вектора
d
и
вектора
{
}
1; 1; 0c =−
равно 1.
8. а) Проекция вектора
d
на вектор
{
}
2; 1; 2a
=
−
равна 4/3, б) проекция
вектора
d
на вектор
{
}
1;1; 0
равна
b =
2 , в) скалярное произведение
вектора
d
и вектора
{
}
3;1; 2c
равно 5.
=
9. а) Проекция вектора
d
на вектор
{
}
1;1; 0a
=
−
равна 0,5 2 , б) вектор
d
ортогонален вектору
{
}
3;1; 2b =
, в) скалярное произведение вектора
d
и
вектора
{
}
1; 6; 2c =−
равно 6.
10. а) Скалярное произведение вектора
d
и вектора
{
}
3; 2; 1a
=
−−
равно 1, б)
проекция вектора
d
на вектор
{
}
1; 1; 1b
=
−−−
равна – 3 , в) скалярное
произведение вектора
d
и вектора
{
}
0;3; 2c
=
равно 4.
11. а) Вектор
d
ортогонален вектору
{
}
1; 1; 0a
=
−
, б) проекция вектора
d
на
вектор
{
}
1;1; 1b =−
равна 3 , в) скалярное произведение вектора
d
и
вектора
{
}
1; 1;1c =−
равно 1.
12. а) Скалярное произведение вектора
d
и вектора
{
}
1;1; 1a =−
равно 2, б)
вектор
d
ортогонален вектору
{
}
0;1; 1b
=
−
, в) проекция вектора
d
на
вектор
{
}
1;1; 2c
равна
=
26
3
.
13. а) Скалярное произведение вектора
d
и вектора
{
}
1;1; 0
равно 1, б)
проекция вектора
d
на вектор
a =
{
}
2;1; 1b
=
−
равна 6/3, в) скалярное
произведение вектора
d
и вектора
{
}
0;1; 2c
=
равно – 1.
18
14. а) Скалярное произведение вектора
d
и вектора
{
}
3; 2;1a =
равно 3, б)
проекция вектора
d
на вектор
{
}
1; 0; 1b
=
−
равна 2/2, в) проекция
вектора
d
на вектор
{
}
2;1;1c
равна
=
6/6.
15. а) Вектор
d
ортогонален вектору
{
}
3;1;1a
=
, б) проекция вектора
d
на
вектор
{
}
2; 1;1b =−
равна 6/3, в) скалярное произведение вектора
d
и
вектора
{
}
1;1; 1c =−
равно – 2.
16. а) Скалярное произведение вектора
d
и вектора
{
}
1; 0; 2a
=
равно – 5, б)
проекция вектора
d
на вектор
{
}
2;1; 2b =
равна 2, в) вектор
d
ортогонален вектору
{
}
1;1; 2c
.
=
17. а) Скалярное произведение вектора
d
и вектора
{
}
1; 1; 3a =−
равно 2, б)
проекция вектора
d
на вектор
{
}
2;1; 1b
=
−
равна 6/6, в) вектор
d
ортогонален вектору
{
}
1; 0;1c
.
=
18. а) Вектор
d
ортогонален вектору
{
}
3;1;1a
=
−
, б) скалярное произведение
вектора
d
и вектора
{
}
2;1; 0b =−
равно – 2, в) проекция вектора
d
на
вектор
{
}
1; 0;1c
равна
=
22.
19. а) Вектор
d
ортогонален вектору
{
}
5; 3; 4a
=
−
, б) скалярное
произведение вектора
d
и вектора
{
}
2;3; 0b =
равно 4, в) проекция
вектора
d
на вектор
{
}
2;1; 2c =−
равна – 1/3.
20. а) Проекция вектора
d
на вектор
{
}
2; 2;1a
=
равна 2, б) вектор
d
ортогонален вектору
{
}
2; 1;1b =−
, в) скалярное произведение вектора
d
и
вектора
{
}
2; 1; 0c =−
равно 5.
21. а) Вектор
d
ортогонален вектору
{
}
3; 5; 1a
=
−
, б) скалярное
произведение вектора
d
и вектора
{
}
1;1; 0b =
равно – 1, в) проекция
вектора
d
на вектор
{
}
2; 6; 3c =−
равна 4/7.
19
