Стронгин Р.Г (ред.) Высокопроизводительные параллельные вычисления на кластерных системах

Подождите немного. Документ загружается.

391

200 400 600 800 1000

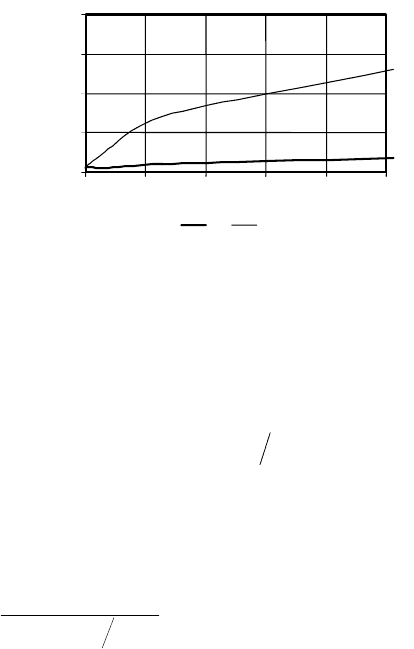
Sn Sn ср

Рис. 6. Ускорение для функции №2

Пусть

- требуемая точность (по каждой координате) поиска

глобального экстремума;

- заданный уровень доверительной

вероятности его обнаружения;

а – размер частичного квадрата, в

котором ищется оптимум. Очевидно, что вероятность обнаружения

глобального экстремума равна

. Вероятность того, что в

окрестности глобального экстремума попадет, по крайней мере,

одна точка, равна

=−−==−=≥

)p(}m{P}m{P 11011

Здесь N – число испытаний. Откуда

)aln(

)ln(

−

Используя полученную формулу, несложно подсчитать ускорение

и эффективность параллельных вычислений на базе метода случайного

поиска, имеющего заведомо одинаковое количество обращений к

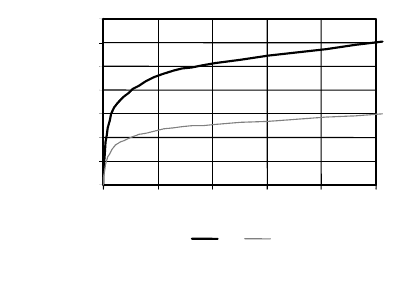
оптимизируемой функции. Из рисунка 7 видно, что наблюдается

существенный рост ускорения и эффективности распараллеливания

процессов. Однако все это происходит на фоне очень низкой

эффективности метода случайного поиска относительно

однопроцессорной схемы. Так

на 256 процессорах эффективность

метода случайного поиска ниже, чем для ЭДАГО на одном

процессоре.

392

Полученные результаты наглядно показывают, что при разработке

параллельных алгоритмов многоэкстремальной оптимизации

необходимо отыскивать иные ресурсы для организации параллельных

вычислений, во всяком случае, нельзя игнорировать адаптивные

механизмы последовательных алгоритмов, повышающие их

эффективность. И действительно они находятся.

100

1000

10000

100000

1000000

10000000

200 400 600 800 1000

Sn En

Рис. 7. Метод случайного поиска

Если исходить из того, что основная доля вычислительных

ресурсов тратится на вычисление функции, то распараллеливать

следует в первую очередь процессы вычисления функции. В алгоритме

ЭДАГО на каждом его шаге делится частичная область

, для

которой характеристическая функция

)

(

в данный момент

принимает наибольшее значение. В принципе ничто не мешает делить

не один сегмент, а первые, например, четыре сегмента с наилучшими

показателями характеристической функции. На следующем шаге опять

первые 4 наилучшие сегмента и т.д. Если алгоритмы деления

сегментов разместить на «своих» процессорах, а обращение к

функциям выполняется только при

делении сегмента, то процесс

деления будет реализовываться на разных процессорах

приблизительно за одинаковое время.

Вычислительные эксперименты с функцией №1 показали, что

ускорение в этом случае достигает величины 3.52 . Это позволяет

сделать вывод о том, что наибольшей эффективности от

распараллеливания алгоритмов можно ожидать, когда параллелизм в

393

явной форме «вшит» в канву модифицируемого алгоритма, в тех

местах, где это наиболее полезно. В этом случае чрезвычайно полезны

явные методы разработки алгоритмов параллельных вычислений,

позволяющие не только описывать алгоритмы, но и исследовать их

корректность.

Литература

1. Андреев А.Н., Антонов А.С., Воеводин В.В., Воеводин Вл.В.,

Жуматий С.А. Комплексный подход к анализу эффективности

программ для параллельных вычислительных систем. //

Седьмая Межд. конфер. "Высокопроизводительные

вычисления и их приложения", Черноголовка, 2000.

Стронгин Р.Г. Численные методы в многоэкстремальных

задачах. – М.: Наука, 1978.

Коварцев А.Н. Автоматизация разработки и тестирования

программных средств // Самар. гос. аэрокосм. ун-т, Самара.

1999.

О НЕКОТОРОЙ ПАРАЛЛЕЛЬНОЙ МОДИФИКАЦИИ

АЛГОРИТМА ОТОБРАЖЕНИЯ ФРАГМЕНТА ЭЛЕКТРОННОЙ

КАРТЫ

З.А. Матвеев

Нижегородский государственный университет

Введение

В данном докладе рассматриваются предварительные результаты,

полученные при распараллеливании алгоритма отображения

фрагмента электронной карты.

Данный алгоритм был разработан в рамках программного

продукта, позволяющего осуществлять просмотр большеформатных

точных электронных карт в векторном формате HPGL (графический

язык, разработанный фирмой Hewlett Packard для управления

плоттерами). Рассматривая задачу просмотра файла в графическом

формате, мы подразумеваем, во-первых, собственно

задачу просмотра

листа карты на экране монитора, и, во-вторых, возможность удобного

перемасштабирования листа карты, возможность удобной навигации в

пределах листа карты.

394

Специфика предметной области такова, что на вход программного

продукта как правило поступает весьма большой объём данных. Так,

вполне типичными являются электронные карты размером в 20-40 Мб,

содержащие описание порядка миллиона графических примитивов. В

то же время, требования к точности генерируемого изображения

достаточно велики, т.к. программный продукт планируется

использовать для детальной

верификации топографической карты.

В связи с упомянутыми ограничениями перед автором была

поставлена задача разработки различных алгоритмов по минимизации

времени, затрачиваемого на построение изображения при сохранении

достаточно высокой степени точности карты. В результате было

создано несколько последовательных алгоритмов а также внутренний

древовидный формат, позволяющие существенно уменьшить время,

затрачиваемое на построение фрагмента электронной

карты, особенно

при большом коэффициенте увеличения.

В дальнейшем автором было принято решение попытаться

распараллелить тот или иной фрагмент разработанных алгоритмов с

тем, чтобы ещё более увеличить производительность приложения. При

этом в качестве среды разработки была выбрана MS Visual C++ 2005,

одним из преимуществ которой является встроенная поддержка

стандрата openMP.

Последовательная версия алгоритма

Исходный распараллеливаемый участок кода может быть записан

в следующей упрощённой форме:

For (i) do

CreateIndex(i)

For (i) do

begin

if inIndex(i) then

begin

Transform(i)

Draw(i, DC)

end

Листинг 1

Рассмотрим подробнее приведённую запись.

Индекс

i в данном случае является номером большеформатного

объекта верхнего уровня (слоя). Дело в том, что в рамках

395

разработанного алгоритма входной векторный формат преобразуется в

древовидную структуру, где корню дерева поставлен в соответствие

объект векторной электронной карты, его прямым потомкам –

объекты-слои, а узлам, расположенным на втором уровне иерархии

(глубины 2) - сложные векторные объекты (ломаные, кривые).

Таким образом, везде в приведённом фрагменте кода

осуществляется перебор лишь объектов верхнего уровня

, которые

являются непосредственными потомками корневого узла. Перебор

остальных объектов осуществляется рекурсивно.

Операция

CreateIndex (i) в этом случае является рекурсивной

процедурой построения индекса для всех потомков

i-го слоя.

inIndex (i) – является операцией проверки на принадлежность

i-го слоя индексному массиву верхнего уровня.

Transform (i) – это рекурсивная операция преобразования

мировых координат в экранные для всех объектов

i-го слоя.

Draw (i, DC) – это рекурсивная операция вывода i-го слоя на

устройство с дескриптором

DC. На нижнем уровне сводится к

последовательности вызовов функций GDI (в основном

Polyline(DC)).

Отсюда легко можно выделить следующие основные разделяемые

ресурсы:

 графические объекты в рамках внутренней древовидной

структуры;

 индексные массивы;

 дескриптор графического устройства (Handle Device Context).

Параллельная модификация алгоритма

На основании анализа алгоритма и разделяемых ресурсов была

предложена следующая параллельная модификация:

396

#pragma omp parallel for

For (i) do

CreateIndex(I, MappingRect(i_THREAD))

#pragma omp parallel

For (i) do

begin

if inIndex_i_THREAD(i) then

begin

Transform(i)

Draw(i, DC_i_Thread)

end

Листинг 2

Здесь MappingRect(i_THREAD) – окно отсечения, поставленное в

соответствие текущему потоку;

inIndex_i_THREAD – индексный

массив потока

i_THREAD.

Основная идея данного алгоритма заключается в том, что мы

разбиваем отображаемую область на N прямоугольных подобластей,

где N – число используемых потоков. Для каждой подобласти строится

свой индексный массив. Каждой подобласти ставится в соответствие

свой собственный DC_i_Thread.

В результате при использовании подобного алгоритма мы

получаем сравнительно небольшое количество совместно

используемых ресурсов:

 индексный массив верхнего уровня;

 окна отсечения;

 Device Context для каждого подокна.

По окончании работы алгоритма изображения с различных DC

совмещаются и результирующий фрагмент выводится на экран.

Можно отметить следующие преимущества разработанного

алгоритма.

 Малое количество совместно используемых ресурсов (только

индексы, и только на верхнем уровне; нет необходимости

синхронизировать саму внутреннюю древовидную структуру

данных; нет необходимости синхронизировать рекурсивные

алгоритмы) - и как следствие меньшее количество

критических секций или замков (точнее их полное

отсутствие).

397

 Сравнительно незначительная модификация исходного

последовательного алгоритма – сохранение ясной структуры

алгоритма.

 Тривиальный способ аккумулирования результатов различных

ветвей алгоритма по их окончании.

 Масштабируемость.

Следует отметить в то же время и одну проблему реализации. Дело

в том, что при индексировании слоёв, лежащих на стыке подобластей,

возникает необходимость дополнительного распараллеливания на

более низком уровне (сложных векторных объектов). В противном

случае слой отображается частично, так, как будто бы он принадлежал

лишь одной подобласти. Данная проблема

находится сейчас в стадии

исследования.

Сравнительный анализ полученных результатов

Для тестирования использовалась рабочая станция на базе

процессора AMD Athlon 64 x2 Dual, объём ОЗУ 1,87Gb.

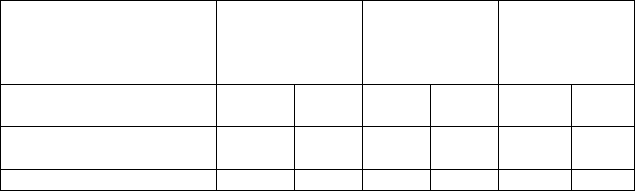
Таблица 2. Сравнительный анализ времени отображения фрагмента карты для

последовательной и параллельной версии алгоритма (мс)

В результате при тестировании первой версии параллельного

алгоритма был отмечен прирост производительности порядка 25%-

30% (см. таблицу 1). Однако необходимо отметить, что данный

прирост наблюдался лишь при работе с картами, разбитыми на

сравнительно крупные слои. На картах, представляющих собой

совокупность небольших слоёв, включающих в себя небольшое

количество объектов, распараллеливание практически не принесло

прироста

производительности, а в отдельных случаях напротив

привело к ухудшению временных показателей (при однократном

Электронная карта 1.plt

(2.048.тыс.

объектов,

2100. слоёв)

2.plt

(471 тыс.

объектов,

7576 слоёв)

3.plt

(386 тыс.

объектов,

8255 слоёв)

Коэффициент

увеличения

1 2 1 2 1 2

Последовательный

алгоритм

187 93 94 63 120 47

Параллельный алгоритм 140 47 63 45 200 63

398

увеличении). Также было отмечено, что значительный прирост

демонстрируется лишь на процессорах AMD.

В связи с неоднозначностью полученных результатов обе версии

алгоритма были подвергнуты анализу с применением

профилировщиков Automated AQTime 5.0 и Intel VTune 9.0. В

результате было выявлено, что сама операция Draw поддаётся

распараллеливанию достаточно плохо (прирост порядка 10%), в то

время как операция Transform в параллельном алгоритме

демонстрирует хороший

прирост производительности (порядка 30-

40%).

На основании данного анализа автор планирует дальнейшую

доработку параллельной версии алгоритма; возможно

распараллеливание будет использоваться лишь на этапе

преобразования координат. В любом случае применение параллельной

версии алгоритма отображения позволило добиться определённого

прироста производительности уже на текущем этапе.

МОДЕЛИРОВАНИЕ ДИНАМИКИ АНСАМБЛЕЙ СЕРДЕЧНЫХ

КЛЕТОК С ИСПОЛЬЗОВАНИЕМ СРЕДСТВ MPI

В.С. Петров, Л.С. Аверьянова, Г.В. Осипов

Нижегородский государственный университет

Введение

Анализ динамических свойств нелинейных сред является сегодня

весьма актуальным и распространенным направлением теоретической

физики. С точки зрения математики, дискретную среду можно

описывать системой большого количества обыкновенных

дифференциальных уравнений (ОДУ), связи между которыми имеют

топологию правильной решетки на плоскости или в пространстве.

Наиболее интересными для исследования являются модели систем,

которые изначально, по

своей физической природе, обладают

свойством дискретности. В качестве примера здесь можно привести

биологические ткани, имеющие клеточное строение. Так, описание и

исследование культуры сердца как дискретной возбудимой среды

особенно актуально с точки зрения медицины. Данный подход

позволяет изучать процессы возникновения режима фибрилляции и

возможные способы ее подавления. Также к пространственно-

дискретным

системам можно отнести кристаллические решетки

399

твердых тел и некоторые искусственные системы: сети синхронизации

(например, в фазированных антенных решетках), решетки

джозефсоновских контактов, искусственные нейронные сети [1].

Следует также заметить, что аналитическое рассмотрение

подобных задач практически не представляется возможным, а

численное моделирование требует очень больших вычислительных

мощностей. При решении наших задач мы использовали

высокопроизводительный кластер факультета ВМК ННГУ

Характеристики кластера следующие.

 Пиковая производительность 2.7 TFLOPS.

 Общий объем оперативной памяти 256 Gb.

 64 вычислительных узла.

 CPU: 2xIntel XEON 5150 Dual Core (4x2.66 GHz cores).

 RAM: 4Gb DDR2.

Постановка задачи

Основной целью работы было исследование динамики больших

регулярных двумерных решеток, состоящих из клеток сердечной

мышцы, описываемых моделью Луо-Руди для мембранного

потенциала клетки. В основе данной модели лежит широко известный

формализм моделей типа Ходжкина-Хаксли [2]. Скорость изменения

потенциала

V, согласно данной модели, определяется выражением:

)(/1

extionicm

IIcV

−=

(1)

Здесь

- мембранная емкость, которая в наших экспериментах

равнялась 1,

ionic

- суммарный ионный ток, протекающий через

мембрану и

ext

- постоянный внешний ток.

ionic

состоит из шести

ионных токов, определяющих динамику изолированной клетки:

быстрый натриевый ток;

- медленный обратный ток;

нестационарный калиевый ток;

- стационарный калиевый ток;

платообразный калиевый ток;

- стационарный фоновый ток.

Величина этих токов определяется шестью так называемыми

«воротными» переменными –

Xfdghm ,,,,,

, которые представляют

собой долю открытого ионного канала и изменяются соответственно

от нуля до единицы. Для нахождения воротных переменных

необходимо решить уравнение вида:

,/)(

yyy

−=

∞

400

где

))()(/(1)),()(/()( VVVVVy

yyyyy

∞

Здесь

y – одна из воротных переменных. Кроме этого, в системе

есть еще одно уравнение для переменной [

Ca]

, определяющей

величину тока

[

Ca]

= -10

-4

+0.07(10

-4

-[Ca]

) .

В итоге мы имеем 8 нелинейных обыкновенных

дифференциальных уравнений, определяющих динамику

изолированной клетки. Детальное описание модели можно найти в

оригинальной статье Луо и Руди [3].

Мы рассматривали решетку размером 600х600 подобных

осцилляторов, которые были диффузионно электрически связаны с

ближайшими соседями, т.е. образовывали регулярную 2D решетку.

Решение систем уравнений динамики подобных сильно

нелинейных

релаксационных систем, как правило, требует применения

таких точных методов численного интегрирования, как, например,

алгоритм Рунге-Кутта четвертого порядка. К сожалению, данный

алгоритм не является оптимальным при использовании параллельных

вычислений. Это связано с тем, что в таком случае на каждом шаге

интегрирования мы вынуждены четыре раза производить

синхронизацию и обмен данными между

различными процессами,

производящими расчет. При достаточно больших размерах

исследуемой системы, это становится существенным фактором,

заметно понижающим скорость и эффективность вычислений.

Учитывая подобные обстоятельства, мы решили использовать

другой алгоритм, специально предназначенный для интегрирования

систем типа (1) и построенный таким образом, что позволяет

осуществлять обмен данными между процессами один раз за

итерацию. Суть

алгоритма сводится к раздельному интегрированию

правой части первого уравнения системы (1) – отдельно нелинейные

функции, описывающие динамику одного элемента, и отдельно

слагаемое, отвечающее за диффузионную связь с другими клетками – а

также использованию адаптивного дробления шага интегрирования в

зависимости от текущего значения производной интегрируемой

переменной. Подробнее об этом алгоритме в [4].

Параллельный алгоритм

Разработка параллельного приложения на основе готового

последовательного кода осуществлялась с использованием MPI.

Основными задачами, которые необходимо было решить, являлись: