Стронгин Р.Г (ред.) Высокопроизводительные параллельные вычисления на кластерных системах

Подождите немного. Документ загружается.

371

увеличится, а сложность алгоритма можно уменьшить, поскольку

определяющее значение имеет не длина ключа, а скорость его смены

генератором псевдослучайных чисел. В приложении 1 приводится

доказательство возможности обеспечить абсолютную криптостойкость

этого шифра, как следствие теоремы Шеннона, утверждающей, что

принципиально невозможно взломать шифр, если длина ключа равна

длине открытого текста при использовании даже

простейшей

логической операции XOR [1].

Если же в системе происходит достаточно быстрая смена ключа

шифра, то для очередной серии блоков применяется уже совершенно

другой ключ, вырабатываемый генератором псевдослучайных чисел, а

прежний уничтожается. Криптостойкость в этом случае определяется:

качеством генератора псевдослучайных чисел. С помощью этого

генератора работает как протокол передачи ключа симметричного

шифра, так и протокол передачи данных, зашифрованных этим

ключом.

Описание протокола

Протокол передачи сеансовых ключей в онлайновом режиме и

шифрованной информации в незащищенной среде приведён в

приложении 2 и включает 4 операции.

КОМПЬЮТЕР-ИСТОЧНИК

: с помощью генератора

псевдослучайных чисел выбирает

два случайных целых числа:

ключ

А для передачи сеансового ключа и сам сеансовый ключ

K для симметричного шифра; вычисляет X

= (A+K) mod 2;

посылает X

в незащищённой сети КОМПЬЮТЕРУ-ЦЕЛИ.

КОМПЬЮТЕР-ЦЕЛЬ: с помощью генератора

псевдослучайных чисел выбирает случайное целое число -

ключ

B для передачи сеансового ключа K; вычисляет

= (B+X

) mod 2; посылает X

в незащищённой сети

КОМПЬЮТЕРУ-ИСТОЧНИКУ.

КОМПЬЮТЕР-ИСТОЧНИК: расшифровывает своим

секретным ключом

, для этого вычисляет

= (A+X

) mod 2; фактически эта операция снимает только

одну "половину" ключа

, поэтому секретный ключ К

остаётся зашифрован ключом передачи КОМПЬЮТЕРА-

Здесь необходимо отметить, что в публикациях, профессионально посвящённых

информационной безопасности, обычно КОМПЬЮТЕР–ИСТОЧНИК называют Алисой,

а КОМПЬЮТЕР–ЦЕЛЬ – Бобом.

372

ЦЕЛИ; посылает

в незащищённой сети КОМПЬЮТЕРУ-

ЦЕЛИ.

4. КОМПЬЮТЕР-ЦЕЛЬ: вычисляет К = (B + X

) mod 2. В

результате КОМПЬЮТЕР-ИСТОЧНИК и КОМПЬЮТЕР-

ЦЕЛЬ оба имеют один и тот же секретный ключ

К, поэтому

могут применять его в любых симметричных алгоритмах,

описанных ранее;

незашифрованный ключ нигде в

незащищённой среде не появляется

Протокол передачи секретных ключей с помощью симметричных

алгоритмов позволяет избавиться от существенных недостатков

существующих протоколов, использующих асимметричное

шифрование. Криптостойкость алгоритма не зависит от его сложности,

поэтому возможно применение простейших операций, выполняемых

процессором очень быстро (по сравнению с асимметричным

алгоритмом - на три порядка). Появляется возможность шифровать

аудио и видеоинформацию в онлайновом

режиме.

Выводы



протокол передачи секретных ключей с помощью

симметричных алгоритмов позволяет избавиться от

существенных недостатков существующих протоколов,

использующих несимметричное шифрование;

 криптостойкость алгоритма не зависит от его сложности,

поэтому возможно применение простейших операций,

выполняемых процессором очень быстро; появляется

возможность шифровать аудио и видеоинформацию в

онлайновом режиме.

В заключение хочу отметить, что использование данной идеи

может найти применение в криптографических системах, в частности,

в создании эффективных протоколов генерации ЭЦП и т.п.

Приложение 1

Как было доказано Шенноном, если длина используемого при

шифровании ключа равна длине шифруемого текста, то такой шифр

является нераскрываемым.

Если же весь текст разбивается на элементарные блоки,

шифруемые каждый своим уникальным непредсказуемым ключом:

373

то зашифрованный текст после преобразования

будет аналогичен тому, который был бы получен в результате

применения одного длинного ключа. Следовательно, зашифрованный

текст не содержит никакой информации об открытом тексте для

криптоаналитика, поэтому может считаться нераскрываемым никаким

методом.

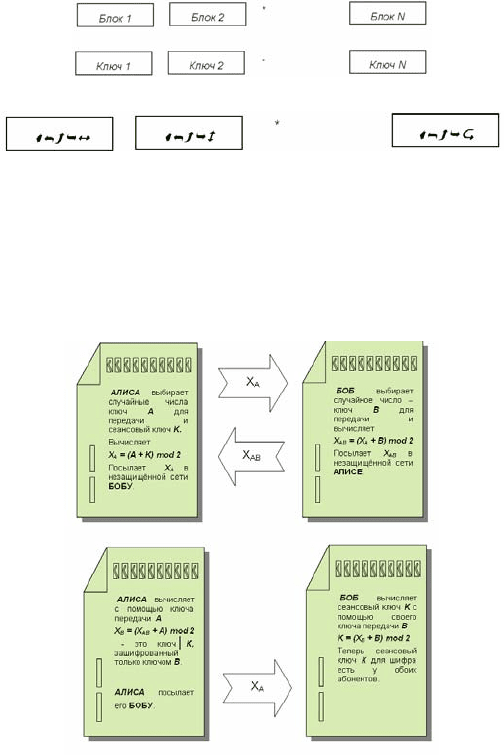
Приложение 2

Схема протокола для передачи сеансовых ключей.

Литература

1. Ярочкин В.И. Информационная безопасность : учебник для

вузов / В.И.Ярочкин. - 2004, М. : Академический Проект :

Гаудеамус. - (Gaudeamus)

374

Кулаков В.И.. и др. Информационная безопасность

телекоммуникационных систем : учебник для вузов / Кулаков

В.И. и др. - 2004, М. : Радио и связь

Садердинов А.А. Информационная безопасность предприятия:

учебное пособие / А.А. Садердинов, В.А. Трайнев и др.. -

изд.3-е. – 2006

Барнс К. Защита от хакеров корпоративных сетей / К. Барнс. -

2005, М. : ДМК Пресс - (Информационная безопасность).

Защита от хакеров Web-приложений/ Дж. Форристал и др.;

пер. с англ. - 2004, М. : АйТи : ДМК Пресс. -

(Информационная безопасность)

Анин Б. Ю. Защита компьютерной информации / Б. Ю. Анин.

- СПб.: БХВ-Петербург, 2000. - 368 с.: ил. - (Мастер. Соврем.

технологии)

ПАРАЛЛЕЛЬНЫЕ АЛГОРИТМЫ МНОГОМЕРНОЙ

РОБАСТНОЙ РЕГРЕССИИ

О.А. Комалева, А.В. Бухановский

Санкт-Петербургский государственный университет

информационных технологий, механики и оптики

Широкое распространение компьютеров с многоядерными

процессорами и кластерных систем на их основе приводит к

необходимости разработки и (или) модификации алгоритмов,

применяемых для решения различных прикладных задач, связанных с

ресурсоемким моделированием или обработкой больших объемов

данных. В частности, к ним относятся параллельные алгоритмы

многомерного статистического анализа [1-2], в том числе, построения

и исследования

регрессионных зависимостей (например, [3]).

В корреляционном приближении для решения регрессионных

уравнений обычно используется метод наименьших квадратов (МНК),

распараллеливание которого не представляет особых сложностей [4].

Однако оптимальность этого метода доказана только при выполнении

строгих статистических предположений об исходных данных;

отклонение от этих ограничений встречается достаточно часто и

приводит к непредсказуемым результатам работы МНК.

Это делает

оправданным использование других методов регрессионного анализа,

эффективность которых слабо зависит от статистических свойств

375

исходных данных, такие методы называются робастными (robust

regression) [5].

В отличие от классических матричных алгоритмов, применяемых

для процедуры МНК, технологии робастной регрессии не допускают

столь очевидного способа распараллеливания. В общем случае они

основаны на решении задачи поиска минимума нелинейной

многомерной функции, ресурсоемкость вычисления которой как

минимум линейно зависит от объема выборочных данных.

работе предлагаются параллельные алгоритмы для нескольких

видов робастной регрессии. Рассматриваются метод наименьших

абсолютных значений (MHAЗ, или

L-регрессия), метод наименьшей

медианы квадратов (МНМК), метод наименьших усеченных квадратов

(МНУК). В общем случае все эти методы сводятся к задаче глобальной

оптимизации функционала, который вычисляется (на основе операции

сортировки), используя вариационный ряд значений невязки.

Для решения задачи оптимизации был выбран алгоритм

рекурсивного случайного поиска (РСП, recursive random search) [6]. Он

состоит из двух вложенных

процедур: изучение (exploration) области, в

которой функционал может принимать минимальное значение, и

эксплуатация (exploitation), или собственно поиск локального

минимума в заданной области. Процедура эксплуатации может быть

проведена независимо на различных областях данных. Как следствие,

вычислительный алгоритм робастной регрессии допускает, как

минимум, два способа параллельной декомпозиции:

распараллеливание процедуры случайного поиска, когда нужно

вычислить

значения целевой функции в нескольких точках, или

непосредственное распараллеливание вычисления значения целевой

функции (процедуры сортировки).

Эксперименты, выполненные на системах с общей памятью,

показали, что распараллеливание процедуры случайного поиска

привносит значительный выигрыш в производительность

(параллельная эффективность 80-90%). В то же время

распараллеливание процедуры расчета целевой функции (быстрая

сортировка [7]) дает существенно меньший эффект (25-30%).

Это

обусловливается тем, что в ходе выполнения программы в процессе

вычисления целевой функции многократно осуществляется переход из

последовательного режима выполнения в параллельный. При

использовании инструментария

OpenMP это требует дополнительных

затрат по времени на порождение и синхронизацию потоков.

376

Важной особенностью вычислительных алгоритмов робастной

регрессии является то, что время их работы меняется от запуска к

запуску, и, по сути, является случайной величиной. При

распараллеливании для оценки эффективности работы этих

алгоритмов возникает необходимость учитывать случайный характер

их параллельного ускорения. Для этого нами использован подход к

описанию эффективности параллельных стохастических алгоритмов

недетерминированным временем работы как в терминах случайной

функции, аргументы которой суть случайные величины с некоторым

законом распределения, зависящим от ряда параметров задачи и

вычислительной системы. В докладе приводятся оценки функций

распределения параллельного ускорения в зависимости от количества

процессоров и особенностей алгоритма случайного поиска.

Литература

1. Boukhanovsky A.V, Ivanov S.V. Stochastic simulation of

inhomogeneous metocean fields. Part III: High-performance

parallel algorithms // Proceedings of ICCS’03, LNCS 2658,

Springer-Verlag, 2003, p. 234-243.

Bogdanov A.V., Boukhanovsky A.V. High performance parallel

algorithms for data processing // Proceedings of ICCS’04, Lecture

Notes in Computer Sciences (LNCS), vol. 3036, Springer-Verlag,

2004.

Gatu C., Kontoghiorghes E.J. Parallel algorithms for computing all

possible subset regression models using the QR decomposition //

Parallel Computing, 29, 2003, pp. 505-521.

Голуб Дж., Лоун Ван Ч. Матричные вычисления. М. Мир,

1999, 548 с.

Rousseuw R.J., Leroy M.A. Robust regresion and outlier detection.

- John Wiley & Sons, 1987 341 p.

Ye T., Kalyanaraman S. A recursive random search algorithm for

large-scale network parameter configuration // Joint International

Conference on Measurement and Modeling of Computer Systems

Proceedings of the 2003 ACM SIGMETRICS international

conference on Measurement and modeling of computer systems. –

NY, USA. ACM Press, 2003. – p. 196-205.

Sanders P., Hansh T. On the efficient implementation of massively

parallel quicksort // Gianfranco Bilardi, Afonso Ferreira, Reinhard

Lüling, José D. P. Rolim (Eds.): Solving Irregularly Structured

377

Problems in Parallel, 4th International Symposium, IRREGULAR

'97, Paderborn, Germany, 1997. – p. 13-24.

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ДИНАМИКИ АНСАМБЛЕЙ

НЕЙРОНОПОДОБНЫХ ЭЛЕМЕНТОВ

НА МНОГОПРОЦЕССОРНОМ КОМПЛЕКСЕ

С ИСПОЛЬЗОВАНИЕМ СРЕДСТВ MPI

М.А. Комаров, А.С. Корнеев, А.К. Крюков, Г.В. Осипов

Нижегородский государственный университет

Введение

Численное моделирование динамических процессов в сетях сильно

нелинейных осцилляторов предъявляет экстремальные требования к

возможностям вычислительной техники. Для задач нелинейной

динамики это обусловлено рядом факторов. Во-первых, для

большинства задач, например по изучению спиральных волн,

образованию и взаимодействию отдельных структур, развитию

пространственно-временного хаоса, необходимо исследовать

пространственные области, достаточные не только для

формирования

и взаимодействия отдельных структур, но и для изучения динамики

коллективных движений таких структур. Учет при этом еще и

двумерности среды приводит к необходимости проводить

исследования в широких диапазонах пространственных переменных.

Во-вторых, различные пространственные возбуждения, наблюдаемые

в нелинейных средах, характеризуются существенно различными

инкрементами, причем многие неустойчивости развиваются лишь на

фоне неоднородных состояний. Так, при исследовании режимов

развитого пространственно-временного хаоса времена выхода системы

на аттрактор, зависящие от пространственных размеров исследуемой

области и близости параметров к точке бифуркации, могут быть очень

большими. Следовательно, и временные масштабы моделирования

велики.

Таким образом, исследование сложных нелинейных процессов в

динамических системах, с одной стороны, практически

не поддается

аналитическому анализу, с другой – при численном моделировании

требует вычислительных средств с высокой производительностью.

Такие средства предоставляет нам кластер ННГУ с

378

производительностью не менее 2.7 TFlops, имеющий 64 узла по 2 Intel

XEON 5150 Dual Core (4x2.66 Ghz ядра) в каждом.

Постановка задачи

В последнее время одной из важнейших задач в теории нейронных

сетей является задача распространения и преобразования информации

ансамблями нейроноподобных элементов, организованных в

различные пространственные структуры. Мы рассматриваем

регулярные решетки локально связанных нейронных клеток, каждая из

которых описывается с помощью математической модели Хубера-

Брауна [1]. Модель представляет собой систему дифференциальных

уравнений четвертого порядка

в форме Коши и описывает динамику

протекания ионных токов через клеточную мембрану и изменение

мембранного потенциала:

Базовое уравнение динамики мембранного потенциала:

srsdrdllm

IIIIVVg

C −−−−−−= )(

Уравнения для быстрых токов:

)()(

dddd

VVagTI

−

)()(

rrrr

VVagTI

−

/))((/

rrr

aaTdtda

−

∅=

∞

Уравнения для медленных токов:

)()(

sdsdsdsd

VVagTI

−

)()(

srsrsrsr

VVagTI

−

/))((/

srsrsr

aaTdtda

−

∅=

∞

/))((/

sdsdsd

aaTdtda

−

∅=

∞

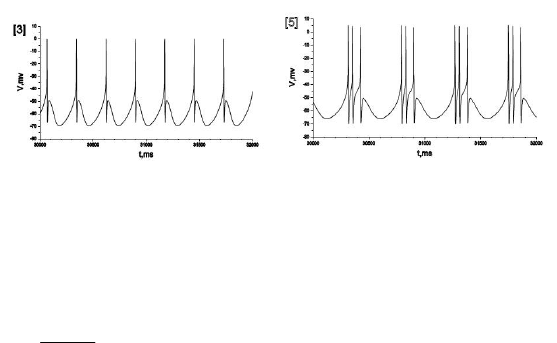
Типичные реализации активности нейронной клетки (изменение

мембранного потенциала), моделируемой уравнениями Хубера-Брауна

приведены на рис. 1.

379

Рис. 1

Локальная электрическая связь между элементами моделировалась

с помощью добавления внешнего синаптического тока в базовое

уравнение динамики мембранного потенциала:

synsrsdrdll

post

IIIIIVVg

C +−−−−−−= )(

)(

postpresynsyn

VVdI

−

pre

- потенциал пресинаптического нейрона, V

post

– потенциал

постсинаптического нейрона и

syn

– проводимость синаптического

канала или сила электрической связи. Таким образом, перед нами

встала задача исследования регулярной решетки, состоящей из 360000

элементов (600 по обоим измерениям), т.е. решения системы из

1440000 обыкновенных дифференциальных уравнений.

Результаты численного расчета

Для решения данной системы дифференциальных уравнений мы

использовали кластер и параллельный алгоритм расчета,

реализованный на языке C c использованием библиотеки MPI. Суть

алгоритма состоит в распределении исходных элементов решетки

между различными процессами и организации обмена и сохранения

данных. Все процессы, за исключением одного, были организованы в

виртуальную двумерную декартову топологию, что впоследствии

облегчило реализацию

алгоритма. Каждый такой процесс получал в

свое распоряжение часть элементов решетки и выполнял вычисления с

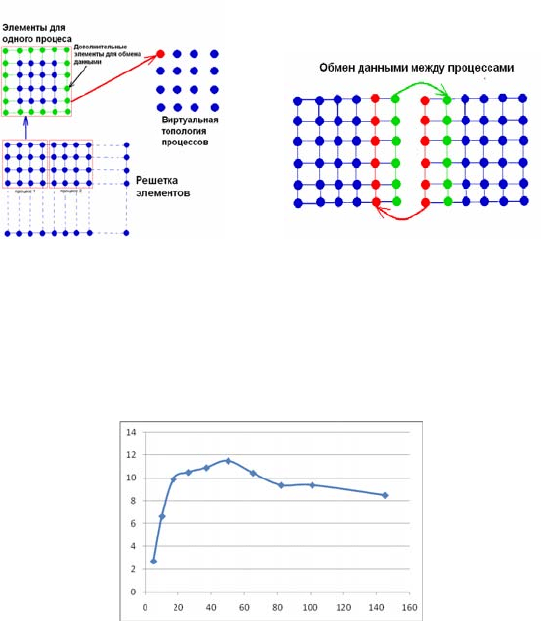
помощью метода Рунге-Кутта 4-го порядка. Схематично

распределение элементов показано на рис.2. Кроме исходных

элементов, каждому процессу добавлялись дополнительные

обрамляющие элементы для учета взаимодействия.

380

Рис. 2

Каждую итерацию соседние процессы обменивались данными по

схеме, изображенной на рис.2. Отдельный процесс не задействовался в

вычислениях, но осуществлял сбор посчитанных данных и сохранение

их на жесткий диск. Результаты тестирования алгоритма на

производительность изображены на рис.3.

Рис. 3

График отображает зависимость отношения времени выполнения

тестовой программы параллельного алгоритма к времени выполнения

последовательного аналога в зависимости от числа используемых

процессов. Максимум отношения равный, 11.9, достигается при 50

используемых процессах.

Численный анализ поставленной задачи показал, что исследуемая

решетка нейроноподобных осцилляторов способна генерировать

волны последовательно синхронной активности, которые участвуют в

преобразовании и распространении информации

[3]. Рис. 4