Стронгин Р.Г (ред.) Высокопроизводительные параллельные вычисления на кластерных системах

Подождите немного. Документ загружается.

351

С учетом последней написанной фразы, после равномерного

перераспределения задач между компьютерами на каждой машине

должно выполняться по три задачи.

Таким образом, значения CI[i] и CJ[j] для испытываемой

нейронной сети будут следующими:

CI[0] = 5;

CI[1] = 4;

CI[2] = 1;

CI[3] = 2;

CJ[0] = 3;

CJ[1] = 3;

CJ[2] = 3;

CJ[3] = 3;

Но для того, чтоб нейронная сеть правильно функционировала,

одним из наиважнейших моментов есть установление правильных

значений коэффициентов A, B, C и D. В настоящий момент

отсутствует общепринятая процедура вычисления подходящих

параметров A, B, C и D [3,5]. Они подбираются на основе опыта

предыдущих результатов, существенно, что такая ситуация не является

особенностью нейронных сетей, это – особенность сложных

оптимизационных задач.

В данном

случае значения коэффициентов были приняты со

следующими значениями: B_k = 1200, C_k = 2000, D_k = 900, AK =

=3000, BK = 500, CK = 2000, DK = 100. Здесь B_k, C_k, D_k –

коэффициенты, использующиеся для определения весов

синаптических связей между нейронами сети, AK, BK, CK, DK –

коэффициенты, использующиеся для внешних смещений нейронной

сети.

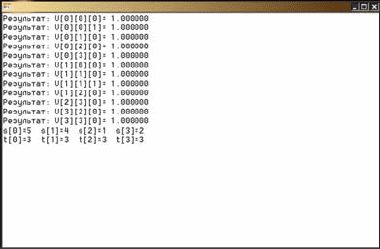
При таких значениях коэффициентов A, B, C и D в результате

функционирования нейронной сети были получены результаты,

представленные на рисунке 1.

352

Рис. 1. Результаты работы нейронной сети

Значения V[i][j][k] = 1 – это значение возбужденного нейрона,

которое в такой сети соответствует тому, что задача из потока

i должна

решаться на

j – м компьютере.

Значения s[i] должны совпадать со значениями CI[i], а значения t[j]

– со значениями CJ[j]. На экране они представлены для подтверждения

правильности вычислений. Поскольку каждое s[i] соответственно

равно CI[i], а значения t[j] соответственно равны значениям CJ[j], то

это гарантирует выполнение заданных в поставленной задаче

ограничений.

Объясним полученные результаты более подробно. Рассмотрим

поток с номером 0. Так как V[0][0][0] = 1, то одна

задача из потока 0

будет распределена на нулевой компьютер, то есть останется решаться

на том же компьютере. Значение V[0][0][1] = 1 указывает на то же, что

и V[0][0][0] = 1, только из данных значений видно, что на нулевом

компьютере будут решаться уже две задачи. Значение V[0][1][0] = 1

показывает, что третья задача из нулевого потока будет решена на

первом компьютере.

Соответственно значение V[0][2][0] = 1 указывает

на то, что четвертая задача из нулевого потока будет решаться на

втором компьютере, а V[0][3][0] = 1, что пятая задача будет

распределена на третий компьютер. Таким образом, поток задач

равномерно распределен на все компьютеры.

Аналогичным образом распределяются задачи между

компьютерами и из всех оставшихся потоков. При этом постоянно

соблюдаются ограничения, накладываемые

на нейронную сеть в

целом.

353

Таким образом, можно сделать вывод, что построенная модель

оптимального распределения потока задач в компьютерной сети на

основе нейронной системы полностью работоспособна и при взятых

экспериментальных значениях работает абсолютно верно, выполняя

необходимую оптимизацию.

Литература

1. Алгулиев Р.М., Алыгулиев Р.М., Алекперов Р.К. Подход к

оптимальному назначению заданий в распределенной системе

// Проблемы управления и информатики, 2004. – №5. – С. 140

– 145.

Нейроматематика: Учебное пособие для вузов. Кн. 6./ Под ред.

А. И. Галушкина. – М.: ИПРЖР, 2002. – 448 с.

Назаров А.В., Лоскутов А.И. Нейросетевые алгоритмы

прогнозирования и оптимизации систем – СПб.: Наука и

техника, 2003. – 384 с.

Ачасова С.М. Вычисления на нейронных сетях //

Программирование, 1991. – №2. – С. 40 – 52.

Козырев Г.И., Лоскутов А.И. Решение задачи коммивояжера

на основе динамической нейронной сети Хопфилда с

подбором коэффициентов синаптических связей

комбинированным генетическим алгоритмом //

Нейрокомпьютеры: разработка, применение, 2001. – №1. –

С.3- 9.

ПАРАЛЛЕЛЬНЫЙ АЛГОРИТМ ГЕНЕРАЦИИ НОРМАЛЕЙ

ПО ПОЛЮ ВЫСОТ

Е.А. Юсов

Нижегородский государственный университет

Введение

В последние годы проблема эффективного распараллеливания

алгоритмов приобрела особую важность, поскольку тактика

наращивания производительности процессоров путем повышения

частоты столкнулась с серьезными проблемами и производители были

вынуждены пойти по пути увеличения числа вычислительных ядер,

расположенных на одном кристалле. Устройствами, которые имеют

сегодня наиболее ярко выраженную параллельную архитектуру,

354

являются графические ускорители. Например, типовая графическая

карта компании NVidia® может содержать от 32 до 128

исполнительных блоков, работающих одновременно. Таким образом, в

распоряжении практически любого пользователя ПК на самом деле

имеется специализированный параллельный вычислительный

комплекс.

Еще одной важной тенденцией в современных компьютерных

технологиях является использование сильно распараллеленного

графического ускорителя для решения неграфических задач,

то есть

задач, не связанных непосредственно с формированием изображения.

В связи с вышесказанным, проблема распараллеливания вычислений в

настоящее время является актуальной и не только при решении очень

сложных задач, которые требуют использования целого

вычислительного кластера. Она также важна при выполнении менее

сложных алгоритмов, выводя их на качественно новый уровень.

Примером такой

задачи является генерация нормалей по полю высот,

которая возникает при моделировании и вузуализации рельефа, а

также других объектов, задаваемых матрицей высот. Предлагаемая

реализация алгоритма с использованием графического ускорителя

наглядно демонстрирует, как эффективно использовать его

параллельную архитектуру.

Описание алгоритма

Исходными данными для алгоритма является матрица высот в

узлах равномерной решетки, размером

mn × , или поле высот. Высоту

в (

i,j) узле решетки будем обозначать через

. В результате работы

алгоритма требуется получить матрицу того же размера, каждый

элемент которой является вектором нормали к поверхности в данной

точке. Возможность эффективной параллельной реализации алгоритма

обеспечивается тем, что нормаль для каждой вершины может быть

вычислена независимо от результатов обработки соседних элементов.

355

(i,j)

(i+1,j)

(i-1,j)

(i,j-1)

(i,j+1)

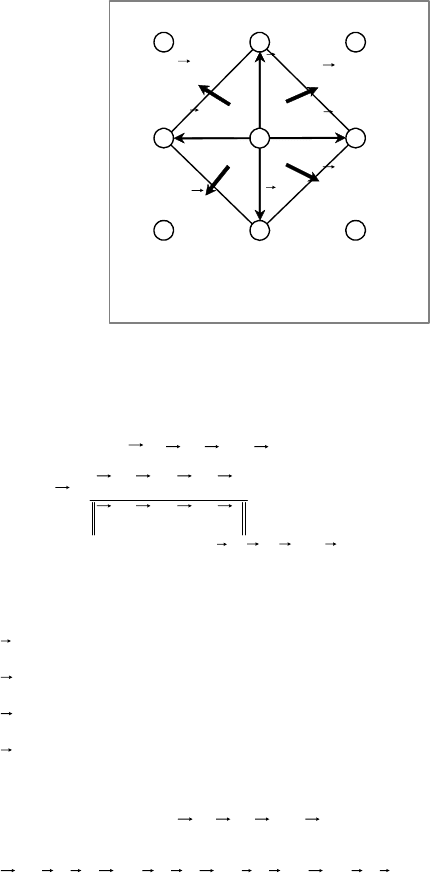
Рис. 1

Вектор нормали для каждой вершины предлагается вычислять как

среднее значение нормалей четырех треугольников, образованных с

его верхним, нижним, левым и правым соседями (Рис.1). Обозначим

эти нормали через

соответственно.

Тогда

4321

NNNN

+++

Далее, обозначим через

вектора, направленные от

текущего узла к левому, правому, нижнему и верхнему соседнему узлу

соответственно. Шаг сетки высот постоянный, обозначим его чере

Тогда:

),0,(

,,1 jiji

hhSL −−=

−

),0,(

,,1 jiji

hhSR −=

),,0(

,1, jiji

hhSB −−=

−

),,0(

,1, jiji

hhST −=

где через

обозначена высота (i,j) узла сетки высот.

Далее, для векторов

можно записать следующие

выражения:

TRN ×=

RBN ×=

BLN ×=

LTN ×=

356

Распишем более подробно компоненты векторов:

)(

,,1

jiji

hhSN −−=

)(

,,1

jiji

hhSN −−=

)(

,,1

jiji

hhSN −−=

)(

,1,

jiji

hhSN −=

−

)(

,,1

jiji

hhSN −=

−

)(

,1,

jiji

hhSN −=

−

)(

,,1

jiji

hhSN −=

−

)(

,1,

jiji

hhSN −−=

Тогда для суммы

4321

NNNN +++

получим следующее

выражение:

)4),(2),(2(

1,1,,1,1

4321

ShhShhSNNNNN

jijijiji

sum

+−+−

−−=+++=

Поскольку вектор

sum

необходимо подвергать нормировке, все

его компоненты можно разделить на 2

S, тогда:

)2,,(

1,1,,1,1

ShhhhN

jijijiji

sum

+−+−

−−=

Таким образом, мы получили простую и удобную и формулу для

вычисления компонентов вектора нормали. Последним шагом является

нормировка полученного вектора.

Реализация

Приведенный алгоритм был реализован при помощи DirectX10®

API с помощью вершинных шейдеров 4 версии. Исходный код

пиксельного шейдера, выполняющего вычисление нормалей,

представлен в Листинге 1.

struct GenerateQuadGS_OUTPUT

{

float4 m_ScreenPos_PS : SV_POSITION;

float2 m_ElevMapUV : TEXCOORD0;

};

float3 GenerateNormalMap_PS(GenerateQuadGS_OUTPUT In) : SV_TARGET

{

// Получаем размеры текстуры, содержащей поле высот

uint ElevMapWidth, ElevMapHeight, Levels;

g_tex2DElevMap.GetDimensions(0, ElevMapWidth, ElevMapHeight, Levels);

float2 ElevMapSize = float2(ElevMapWidth, ElevMapHeight);

// Считываем высоты левого, правого, верхнего и нижнего соседних

элементов из текстуры. samPointClamp – сэмплер, выполняющий

точечную фильтрацию текстуры

float Height1 = g_tex2DElevMap.SampleLevel(samPointClamp,

In.m_ElevMapUV.xy + float2(1/ElevMapSize.x, 0), 0);

float Height2 = g_tex2DElevMap.SampleLevel(samPointClamp,

In.m_ElevMapUV.xy - float2(1/ElevMapSize.x, 0), 0);

float Height3 = g_tex2DElevMap.SampleLevel(samPointClamp,

357

In.m_ElevMapUV.xy + float2(0, 1/ElevMapSize.y), 0);

float Height4 = g_tex2DElevMap.SampleLevel(samPointClamp,

In.m_ElevMapUV.xy - float2(0, 1/ElevMapSize.y), 0);

// Вычисляем нормаль

float3 SummN;

SummN.x = Height2 - Height1;

SummN.y = Height4 - Height3;

SummN.z = g_fCellEdgeLen * 2.f;

float3 Normal = normalize( SummN );

return Normal;

}

Листинг 1. Исходный код пиксельного шейдера, выполняющего вычисление

нормалей

Для запуска алгоритма необходимо установить 4-канальную

текстуру, компоненты

r, g, и b которой будут содержать координаты

вектора нормали, в качестве внеэкранного буфера, и вызывать команду

Draw() (компонента a не используется). Отображаемой геометрией

является прямоугольник, точно покрывающий всю текстуру. В

результате, в процессе выполнения команды графической картой,

пиксельный шейдер будет вызван для каждого тексела

обрабатываемой текстуры и в него будет записана вычисленная

нормаль.

Поле высот ландшафта содержится в текстуре

g_tex2DElevMap,

каждый ее элемент является числом с плавающей точкой формата

float. Входными данными для шейдера является структура,

содержащая координаты обрабатываемого тексела в экранном

пространстве, а также текстурные координаты соответствующего

элемента карты высот. Для получения значений элементов поля высот

используется встроенная функция

SampleLevel(), позволяющая

прочитать данные из текстуры по заданным координатам. Чтобы

считать данные соседнего тексела, необходимо изменить

соответствующую текстурную координату текущего тексела на

значение равное 1, деленной на размер текстуры, - что и делается в

шейдере.

Преимуществом реализации данного алгоритма на графическом

процессоре является еще и то, что все данные находятся в

видеопамяти, и

нет необходимости в пересылке их из системной

памяти через медленную шину PCI-E.

Заключение

Мы продемонстрировали, как задача вычисления карты нормалей

по полю высот может быть эффективно распараллелена и реализована

358

на графическом процессоре. Представленный алгоритм был успешно

использован в системе визуализации рельефа, описанной в [1].

Литература

1. Yusov E., Turlapov V.E. GPU-optimized efficient quad-tree based

progressive multiresolution model for interactive large scale terrain

rendering // Conference Proceedings of the 17th International

Conference on Computer Graphics and Vision “GraphiCon’2007”

p. 53-60, Moscow, June 23-27, 2007.

ПРОБЛЕМЫ МОДЕЛИРОВАНИЯ ДИНАМИКИ ЧАСТИЦ

В ЦИКЛИЧЕСКИХ УСКОРИТЕЛЯХ

С.Н. Андрианов

Санкт-Петербургский государственный университет

Введение

Современные задачи физики ускорителей приводят к

необходимости проведения на начальном этапе проектирования

многочисленных вычислительных экспериментов, на основе которых

как разрабатываются конструктивные проекты, так осуществляется

текущее управление уже существующими установками. Именно

тщательное предварительное моделирование (как математическое, так

и компьютерное) является практически единственным инструментов

для исследования всех процессов, на основе которых осуществляется

функционирование

ускорителей, поскольку натурный эксперимент для

такого рода установок практически не реализуем в силу его

дороговизны. Объем вычислений, необходимый для реализации

соответствующих вычислений, требует использования

высокопроизводительной вычислительной техники для получения в

достаточной мере адекватных результатов. Сложность физической

задачи приводит к необходимости тщательного отбора

математических моделей, позволяющих проводить как качественный,

так и

количественный анализ нелинейных процессов различной

природы. Особое значение приобретают методы и средства

компьютерной алгебры, поскольку с одной стороны исследователь

получает возможность аналитического анализа возможных вариантов

системы управления пучками частиц, с другой – существенно

повышает эффективность проводимых численных исследований с

359

использованием современной вычислительной техники. Иными

словами, математический аппарат, используемый в физике пучков,

должен обеспечивать возможность проведения качественного анализа

нелинейной динамики, синтеза оптимальных систем управления на

основе эффективных вычислительных экспериментов с

использованием технологии параллельных и распределенных

вычислительных систем.

В настоящей работе в качестве математического аппарата

рассматривается матричный формализм для алгебраических методов

Ли [1]. Матричный формализм позволяет строить конструктивные

алгоритмы построения операторов эволюции пучка частиц при

описании динамики пучков частиц, как с учетом нелинейных внешних

(управляющих), так и собственных полей. Именно подобный подход

позволяет эффективно использовать технологии распараллеливания и

распределения вычислительных операций.

В настоящей работе используются два понятия:

параллельные и

распределенные вычисления. Под первым типом мы будем понимать

процедуру выполнения однородных операций по возможности с

использованием однородных вычислительных систем. Второй тип

предполагает, что в исходной задаче проведена декомпозиция на две

группы вычислительных потоков. Первый тип состоит из независимых

(слабо зависящих) вычислительных потоков. В качестве простого

примера второго типа можно привести два вычислительных

потока:

первый позволяет проводить вычисления по динамике частиц в пучке,

второй – с использованием полученных в первом потоке данных,

осуществлять их обработку для получения каких-либо

вспомогательных результатов, например, визуализации динамики

частиц.

Несмотря на то, что эффективность предлагаемого подхода в

полной мере проявляется в задачах, допускающих применение

методов теории возмущения, следует

отметить, что данный класс

задач достаточно представителен и находит свое отражение в самых

различных областях физики ускорителей.

Основные представления и понятия

Рассмотрим основные понятия матричного формализма для

алгебраических методов Ли. В качестве математической модели

динамики пучков частиц рассматривается задача Коши для системы

обыкновенных дифференциальных уравнений следующего вида

360

,)(),,,,(

)(

000

Μ∈== XXBUXF

(1)

где

-мерный фазовый вектор, описывающий состояние

частиц пучка,

)(tU

-мерная вектор-функция, описывающая

управляющие (внешние) электромагнитные поля и

-мерный

вектор управляющих параметров (определяющих функционирование

системы),

- независимая переменная, в качестве которой обычно

выбирается длина, измеряемая вдоль некоторой (опорной) кривой. Мы

будем также предполагать, что функция

),( tXF

допускает разложение

в ряд в окрестности точки

. Пусть

- множество начальных

данных, описывающее начальное состояние пучка как совокупности

частиц. Обычно в ускорительных системах число частиц

лежит

в пределах

]10,10[

1610

∈N

. Очевидно, что непосредственное

интегрирование системы (1) для столь большого набора начальных

данных не является возможным даже при использовании

суперкомпьютеров. Уравнению (1) сопоставим операторное уравнение

вида

,),()(,)|(),|()(

)|(

000

∂

===

ttLIdttMttMtL

ttdM

(2)

где

- тождественный оператор и

)(tL

- оператор Ли [1].

Оператор

)|(

ttM

будем называть оператором эволюции

(пропагатором), так как имеет место равенство

.,)|()(

0000

Μ∈∀= XXX ottMt

После введения базиса Пуанкаре-Витта

},,,,,1{

][]2[

XXX

, где

4434421

XXXX ⊗⊗⊗=

][

- кронекерова степень вектора

, содержащая

все мономы

-порядка относительно компонент вектора

уравнения движения частиц (1) можно переписать в следующем виде

(для простоты записи опускаем

BU,

∑

∞

][1

)(),(

)(

XPXF

, (3)

где матрицы

)(

описывают нелинейные эффекты

-го порядка

и легко могут быть вычислены в символьном виде (при известной