Стронгин Р.Г (ред.) Высокопроизводительные параллельные вычисления на кластерных системах

Подождите немного. Документ загружается.

381

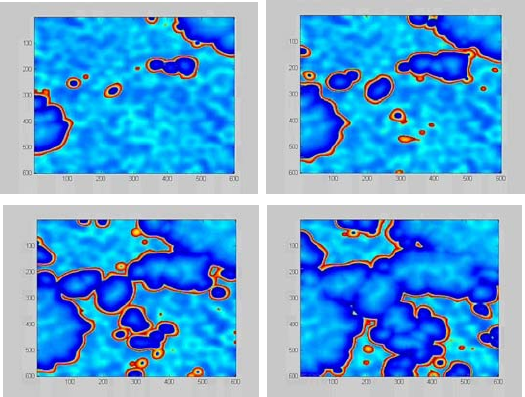
иллюстрирует взаимодействующие волны синхронного возбуждения в

решетке в различные моменты времени.

Рис. 4

Подводя итог, отметим, что программный продукт использующий

преимущества параллельного программирования и высокую

производительность метакластера является весьма эффективным

средством для изучения процессов, происходящих в дискретных

активных средах.

Работа выполнена при финансовой поддержке РФФИ-ННС, проект

05-02-90567, РФФИ-МФ проект 05-02-19815 и РФФИ проект 06-02-

16596.

Литература

1. Braun H.A, Voigt K, Huber M.T (2003) Oscillations, Resonances

and Noise: Basis of Flexible Neuronal Pattern Generation.

Biosystems

71: 39-50.

Sosnovtseva O.V., Postnova S.D., Mosekilde E., Braun H.A. Inter-

pattern transitions in a noisy bursting cell. Fluctuation and Noise

Letters Vol. 4, No. 3. 2004.

382

Mikhail I. Rabinovich et al. Dynamical principles in neuroscience.

Reviews of modern physics, volume 78. October-December. 2006.

ВОЗМОЖНОСТИ РАСПАРАЛЛЕЛИВАНИЯ ВЭЙВЛЕТНО-

СПЛАЙНОВОГО СЖАТИЯ НА НЕРАВНОМЕРНОЙ СЕТКЕ

Ю.К. Демьянович, О.М. Косогоров, А.А. Макаров

Санкт-Петербургский государственный университет

Введение

Известно, что на двукратно измельчающейся сетке

полиномиальные B-сплайны образуют телескопическую систему

пространств, на основе которой строятся вэйвлетные разложения (см.

[1-5]); для равномерной сетки это устанавливается с помощью

преобразования Фурье (см., например, [3]), а для неравномерной сетки

- использованием специального дробно-рационального тождества (см.

[6-8]) и калибровочных соотношений [6, 9]. Применение

неравномерной сетки позволяет улучшить приближение

функций без

усложнения вычислений. Однако, для дальнейшего улучшения

приближения, могут понадобиться различные степени измельчения

сетки в разных частях рассматриваемого промежутка

: для этого

двукратное измельчение недостаточно.

Особую заботу представляет

вэйвлетное разложение в случае неравномерной сетки, поскольку

обычно применяемое на равномерной сетке преобразование Фурье в

условиях неравномерной сетки использовать затруднительно.

Оказалось, что использование биортогональной системы

функционалов позволяет построить вэйвлетные разложения при

произвольном измельчении сетки (это ведет к упрощениям и в случае

равномерной сетки).

В данной работе рассматривается вэйвлетное разложение

телескопической системы пространств В-сплайнов второй степени при

произвольном способе измельчения сетки (вывод формул см. в работе

[8]). Первоначально с каждой сеткой связываются B-сплайны

второй

степени. Если новая сетка получена из исходной удалением одного

узла, то пространство минимальных сплайнов, построенных для

крупной сетки, содержится в пространстве аналогичных сплайнов,

построенных для мелкой сетки. Использование биортогональной (к B-

сплайнам) системы функционалов позволяет получить прямое сплайн-

вэйвлетное разложение и соответствующие формулы декомпозиции и

383

реконструкции; отсюда следует, что последовательное удаление или

добавление узлов в исходную сетку приводит к телескопическим

системам пространств рассматриваемых сплайнов и к прямому

разложению исходного пространства. От исходной сетки можно

перейти к любой более мелкой сетке добавлением любой конечной

совокупности узлов, не совпадающих с узлами расширяемой сетки

(между любыми двумя узлами

исходной сетки число добавляемых

узлов может быть различным в зависимости от выбранной пары

соседних узлов). Формулы декомпозиции и реконструкции

получаются использованием соответствующих биортогональных

систем функционалов. Все результаты верны в случаях конечного

отрезка и бесконечного интервала.

Сжатие модельных числовых потоков

Предлагается алгоритм, который целесообразно использовать для

обработки больших потоков числовой информации с резко

меняющимися характеристиками. В первом приближении упомянутые

числовые потоки характеризуются наличием регулярной и

сингулярной частей. Сжатие информации может быть осуществлено

путём отбрасывания потока с несущественной информацией (при этом

важно грамотно выделить поток с несущественной информацией из

исходного информационного потока

в каждом отдельном случае).

Алгоритм восстановления позволяет провести восстановление с

потерей (т.о. сжав информацию) или (при необходимости) полностью

восстановить исходный числовой поток.

Написана программа на языке C++, реализующая сжатие и

восстановление модельных числовых потоков. Некоторые результаты

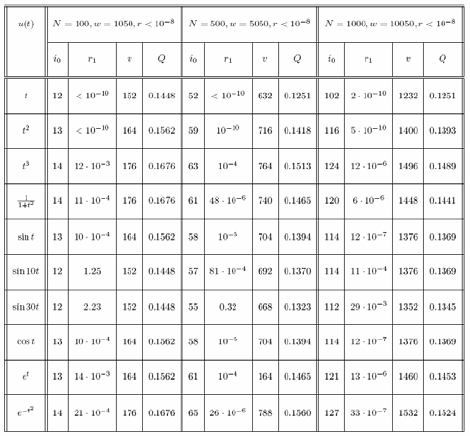
работы этой программы приводятся в следующей таблице:

384

Таблица 1.

Программная реализация декомпозиции и реконструкции показала

быструю и эффективную работу алгоритма на ряде модельных

примеров.

Также рассматривается возможность распараллеливания

предлагаемого алгоритма. Предлагается параллельная версия,

позволяющая полностью загрузить двухъядерную или

двухпроцессорную архитектуру и допускающая эффективную

программную реализацию.

Литература

1. Петухов А.П. Введение в теорию базисов всплесков. СПб.

1999. 132 с.

Добеши И. Десять лекций по вейвлетам. Москва-Ижевск.

2004. 404 с.

Чуи К. Введение в вейвлеты.-М.: Мир, 2001.- 412 с.

Малла С. Вэйвлеты в обработке сигналов. М. 2005.671 с.

Новиков И.Я., Стечкин С.Б. Основы теории всплесков //

Успехи математических наук.-1998. - Т.53.- № 6 (324). - С. 53-

128.

385

Демьянович Ю.К. Калибровочное соотношение для B-

сплайнов на неравномерной сетке// Математическое

моделирование.- 2001.- Т.13.- № 9.- С. 98-100.

Демьянович Ю.К. Всплесковые разложения в пространствах

сплайнов на неравномерной сетке //Докл. РАН.-2002.- Т.382.-

№ 3. - С.313-316.

Демьянович Ю.К. Локальный базис всплесков на

неравномерной сетке // Записки научных семинаров ПОМИ. –

2006. - Т.334. - С.84-110.

РАЗРАБОТКА ПАРАЛЛЕЛЬНОГО АЛГОРИТМА

МНОГОЭКСТРЕМАЛЬНОЙ ОПТИМИЗАЦИИ ФУНКЦИЙ

МНОГИХ ПЕРЕМЕННЫХ

А.Н. Коварцев

Самарский государственный аэрокосмический университет

им. С.П. Королева

Организация параллельных вычислений - один из наиболее

перспективных способов повышения эффективности разрабатываемых

программных продуктов. Несмотря на очевидность преимуществ от

распараллеливания вычислительных процессов, данная схема

организации управления вычислениями чревата значительными

проблемами [1]. Проблема организации параллельных вычислений

носит комплексный характер. Здесь переплетаются в один клубок

проблемы, связанные с конфигурацией компьютера, эффективностью

его системного программного окружения

, структурной

эффективностью самой программы организации параллельных

вычислений. Часто достаточный ресурс параллелизма содержится в

самом алгоритме организации вычислений. Однако в этом случае при

разработке алгоритма необходимо изначально учитывать фактор его

параллельного исполнения, а не пытаться разложить на параллельные

процессы уже имеющуюся последовательную программу решения

исходной задачи.

Рассмотрим проблемы разработки параллельных алгоритмов

на

примере задачи многоэкстремальной оптимизации функций многих

переменных. Выбор области исследований обусловлен двумя

причинами. Во-первых, методы глобальной оптимизации имеют

большое количество практических приложений. Во-вторых, алгоритмы

386

оптимизации для функций многих переменных становятся

чрезвычайно трудоемкими, и единственным способом повышения их

производительности является распараллеливание вычислительных

процессов.

В качестве объекта исследований выберем, разработанный

автором, эвристический, двоичного деления, алгоритм глобальной

оптимизации (ЭДАГО). Идея численного метода во многом

основывается на методе характеризации, предложенного Р.Г.

Стронгиным для решения задач многоэкстремальной оптимизации

функций одной переменной [2]. Для простоты рассмотрим задачу

двумерной многоэкстремальной оптимизации.

Пусть областью поиска глобального максимума является

единичный квадрат

]

;

[

]

;

[

1010

. В дальнейшем область D

подвергается последовательному двоичному делению на подобласти

таким образом, что в центрах каждой из подобластей содержится

точка

)y,x(X

iii

′

, в которой вычисляется значение

оптимизируемой функции, а

. Каждое следующее (j+1)-е

деление области

производится перпендикулярно относительно

направляющего вектора

1−

−

jjj

XXa

. Центры двух новых

областей можно определить из системы уравнений:

⎪

⎩

⎪

⎨

⎧

=−

,/hXX

,)X,a(

jjj

где

- длина направляющего вектора

. На рисунке 1

схематично представлен процесс деления области

D на подобласти.

Его можно интерпретировать как один из методов редукции задачи

оптимизации функции двух переменных к одномерной задаче, с

помощью «ветвящихся», непересекающихся, древообразных ломанных

кривых, всюду плотно покрывающих исходную область

Тогда в вычислительной схеме алгоритма можно использовать

характеристическую функцию, предложенную Р.Г. Стронгиным:

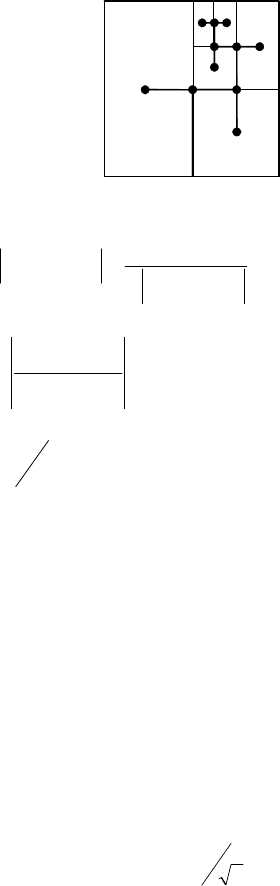
387

Рис. 1

)zz(

XXm

)zz(

XXm)i(R

−

+−=

+ 1

где

⋅

maxM

−

В качестве критерия остановки работы алгоритма использовалось

условие

del

≤

, где

del

- количество уровней двоичного

деления (размер «зерна», не подлежащего дальнейшему делению).

Алгоритм ЭДАГО показал неплохие результаты при оптимизации

функций размерности

≤

. Дальнейшее увеличение размерности

функции требует значительных затрат вычислительных ресурсов ЭВМ

на вычисление функции в центрах локальных областей. Повысить

размерность оптимизируемой функции можно только за счет

распараллеливания вычислительных процессов. Исследования

проводились в предположении, что наиболее трудоемким процессом

является вычисление функции в точках деления.

Исследование распараллеливания вычислительных процессов

производилось на двух тестовых

функциях для случая поиска

глобального максимума функции двух переменных:

Griewank - непрерывная функция, имеющая один глобальный

экстремум и множество локальных экстремумов, близких по

своей величине к глобальному

40010

+⋅−+−= )

cosxcos/)yx((z

]

;

[

2020

−

∈

388

Функция, имеющая 19 локальных экстремумов и один

глобальный, случайным образом распределенных на

единичном квадрате

∑

−

−=

010

)

)XX(

exp(kz

- максимумы функций

)

)XX(

exp(

010

−

];

[

∈

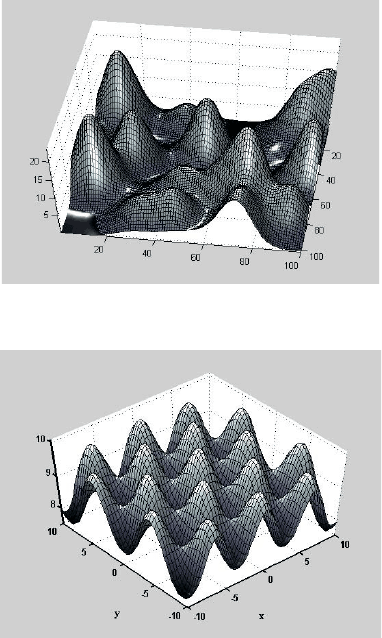
На рисунках 2 и 3 представлены образы тестовых функций.

При разработке параллельного алгоритма, первой приходит мысль

– разбить исходную область поиска на частичные подобласти, в

каждой из которых параллельно организовать поиск глобальных

экстремумов. Тогда глобальным экстремумом исходной области

является одним из глобальных экстремумов ее подобласти. Мотивом

для данного способа организации параллельных вычислений

является

очевидное уменьшение числа экстремумов в каждой из подобластей,

что должно повышать производительность оптимизационных

алгоритмов.

Однако, как это не странно, для данного метода построения

параллельного алгоритма, не наблюдается сколько-нибудь

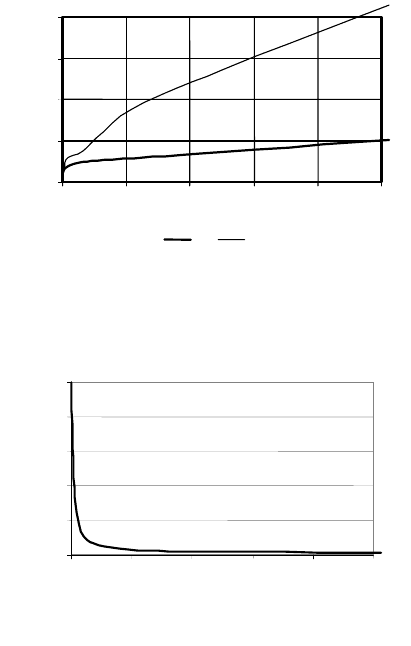
значительного ускорения вычислительного процесса (см. рис. 4, 5). Из

рисунка 4 видно, что при количестве процессоров n=1000, достигается

всего лишь 10-кратное ускорение, при этом эффективность

распараллеливания составляет 0.01. Для тестовой функции №2

результаты еще менее обнадеживающие (см. рис. 6). При n=1000

ускорение равно 3.5, а эффективность – 0.003. С чем же связаны столь

неожиданные результаты?

389

Рис. 2. Тестовая функция №1

Рис. 3. Тестовая функция №2

Алгоритм глобальной оптимизации является адаптивным

алгоритмом и независимо от количества экстремумов какое-то время

требуется для его адаптации к наблюдаемым свойствам

оптимизируемой функции. Косвенно это подтверждается характером

графиков ускорений

срn

(см. рис. 4, 6), посчитанных на основе

среднего времени поиска оптимума по совокупности процессоров.

Видно, что если бы на всех процессорах оптимизация реализовалась

за одинаковое время, то ускорение для функции №1 было бы равно 40,

а для функции №2 – 25.

390

Для проверки этого предположения был выбран самый простой

алгоритм, не обладающий адаптивными свойствами, – метод

случайного равномерного поиска.

200 400 600

800 1000

Sn Sn ср

Рис. 4. Ускорение для функции №1

0,2

0,4

0,6

0,8

200 400 600

800 1000

Рис. 5. Эффективность для функции №1