Stevenson J. Power system analysis
Подождите немного. Документ загружается.

7.8 TRIANGULAR FAORIZATION
277
Example 7.9. Using the triangular factors of
Y
nUS' determine the voltage at bus
of Fig. 7.11 when the current source at bus @ is changed to 14 = 0.60/
-1200
per unit. All other conditions of Fig. 7.11 are unchanged.
Solution . The
Y
n
u
s
for the network of Fig. 7.11 is given in Example 7.3. The
corresponding matrix L may be assembled column by column from Example 7.7
simply by recording the column which is eliminated from the coecient matrix at
each step of the forward-elimination procedure. Then, substituting for L and the
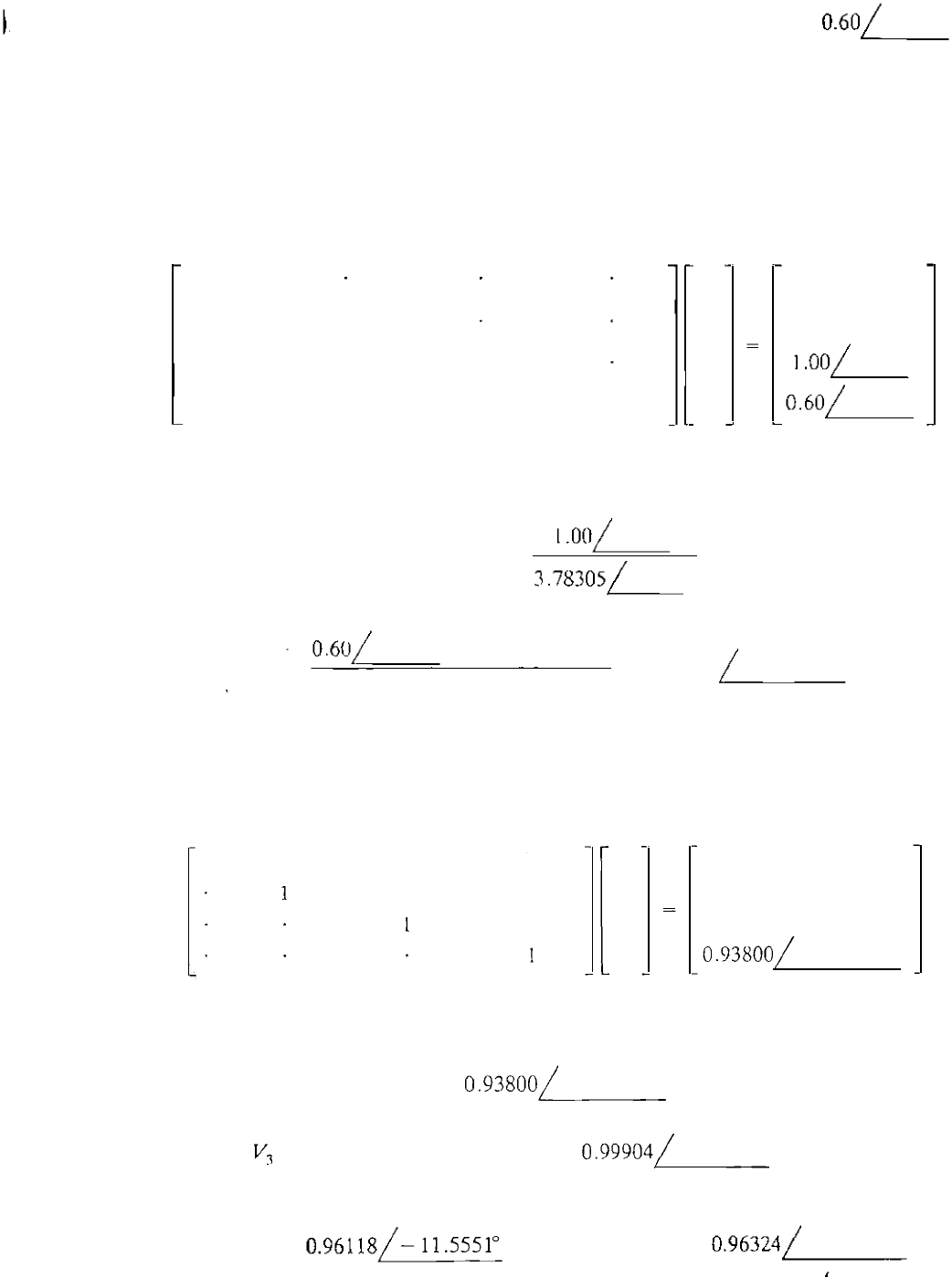
new current vector I in the equation LV '
=
I, we obtain
-jI6.75
V'
I
0
j 11.75
-j 1 1 .00746
V2
0
j2.50
j4.25373
-j3 .78305
V:
.l
1.00/
- 900
j2.50
j6.75373
j
2 .98305
-j1 .43082
r/I
�
0.60/
-1200
Solution by forward substitution beginning wit h V( yields
V( = V2
=
0;
1.00
/
-900
V
' -
-
= 0.26434
.
'
-
3.78305
/
-900
0.60
-120° - (j2 .9S305 )V;
/
V; =
=
0.93800 -12.9163°
-j1 .43082
----
The matrix U is shown directly following Step 4 of the forward elimination in
Example 7.7. Substituting U a n d the calculated entries of V' in the equation
UV = V' gives
1
-0.70 149
-0. 14925
-0.14925
V
I
0
- 0.38644
-0.6D56
V
2
0
-0.78853
V
0
.26434
V4
0 .93800/
-
1 2.91630
w
h ich \Ve may solve by back substitution to obtain
V4 = V; =
0.
93800/
-12.9163° per unit
=
0.26434 -(-0.78853)
V
4
=
0.99904/ -9.5257° per unit
If
desired, we may continue the back substitution using the values for V) and V4 to
evaluate V
2
=
0.96118/- 11.55510
per unit and V
I
=
0.96324/
-11 .43880 per
unit.
278
CHAPTER 7 THE ADMITTANCE
MODEL AND
NETWORK CALCULATIONS
When the coecient matrix
Y
bu
s
is symmetrical, which is almost always the
case, an important simplication results. As can be seen by inspection of Eq.
(7.68), when the rst column of L is divided by Yl1, we obtain the rst row of U;
when the second column of L is divided by Yi�\ we obtain the second row of U;
and so on for the other columns and rows of Eq. (7.68), provided �j
=
�'
i
'
Therefore, dividing the entries in each column of L by the principal diagonal
element in that column yields U
T
whenever
Y
"us is symmetrical. We can then
write
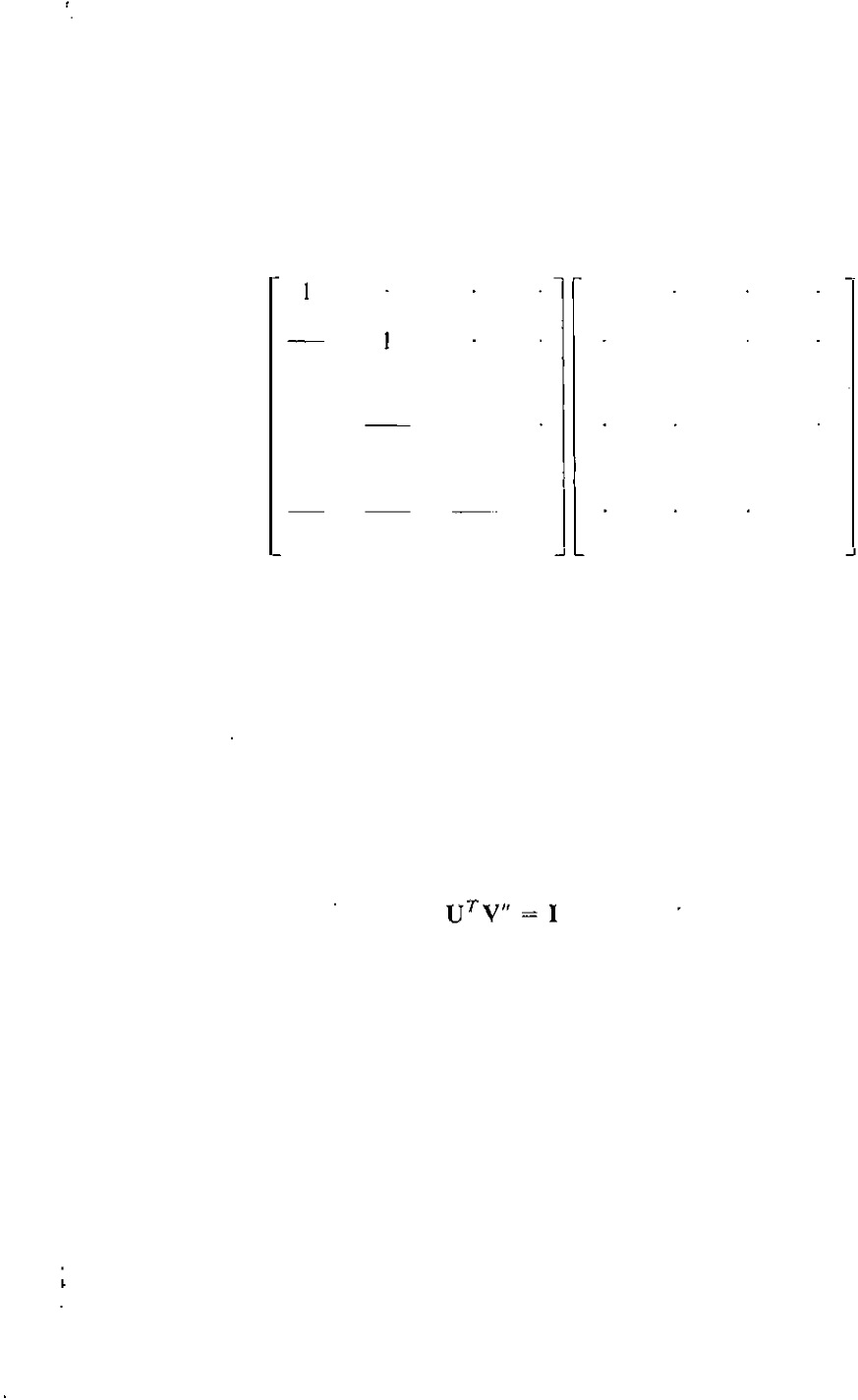
Y
II
Y
2I
y(l)
Y
I
I
22
L
=
uTn =
Y3
1
y
(l)
(7.75)
32
1
y
(
2
)
-
Y
II
y(l)
33
22
�
l
yO)
y(
2
)
4
2
4
3
1
y
(
3
)
Y
l
l
yell
y(
2
)
44
22
33
where diagonal matrix D contains the diagonal elements of L. Substituting in
Eq. (7.71) for L from Eq. (7.75), we obtain the nodal admittance equations in
the
f
orm
Y
V
=
uTnuv
=
I
b
u
s
(7.76)
Equation (7.76) may be solved for the unknown voltages V in three consecutive
steps as follows:
(7.77)
nv'
=
V"
(
7 .78)
= V'
(7.79)
These equations will be recognized as an extension of Eqs. (7.72). The interme
diate
result V" is rst found from Eq. (
7.77) by forward substitution. Next, each
entry in V' is calculated from Eq. (7.78) by dividing the corresponding element
of V" by the appropriate diagonal element of n. Finally, the solution V is
;obtained from Eq. (7.79) by back substitution as demonstrated in Example 7
.9.
Example 7.10. Using Eqs. (7.77) through (7.79), determine the solution vector V of
unknown voltages for the system and operating conditions of Example 7.9. ·
7. SPARSITY AND NEAR-OPTIMAL ORDERING
279
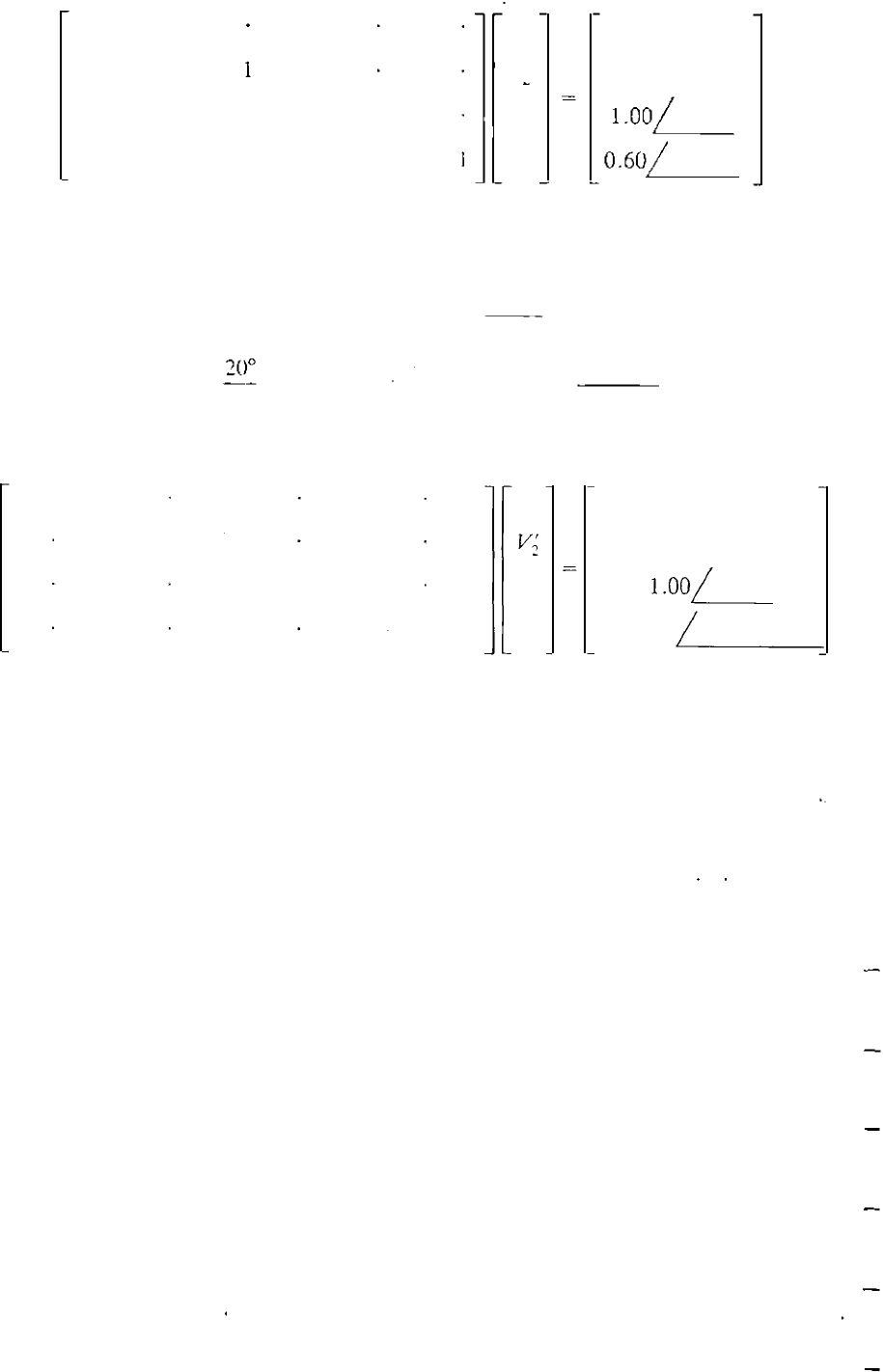
Solution. Substituting in Eq. (7.77) from the current vector I and matrix U of
Example 7.9, we obtain
1
V"
1
0
- 0.70149
V�'
0
-0.14925
- 0.38644
1
V"
1.00/
-900
- 0.14925
-
0.61 3
5 6
- O.7RR53
V"
4
0.60/ - 1200
Straightforward solu tion of this system of equations yields
v;' 'c V�' = 0
v;'
=
I .()O i
-9()0 per unit
v; ' = O.(loL-.�
O.7XXll;' = I .342 rO�02 .91 64° per unit
Substituting for Y" in Eq. (7.78) lencis to the diagonal system
- j16 .75
-j 11.00746
-j3 .78305
-j1 .43082
V'
1
V'
3
V'
4
o
o
1 .00/
-90°
1.34210
/
-102.9164°
the solut ion of which is exactly equal to V' of Example 7.9, and so the remaining
steps of this example match those of Example 7.9.
7.9 SPARSI AND NEAR-OPTIMAL
ORDERING
Large-scale power systems have only a small numher of transmiSSion lines
connected
- 2008 — 2025 «СтудМед»
