Stevenson J. Power system analysis
Подождите немного. Документ загружается.

7.5 THE NETWO RK INCIDENCE MATRIX AND
"
s
257
(b) Now we must reconnect to the network the uncoupled branches, each of
which has an admittance (jO.25)-
1
= -j4.0 per unit. Accordingly, to reconnect
the branch between nodes and , we add to
Y bus
the change matrix
W-
I
-1
6
Y
bus
=
( -j4.0)
-
1
1
@
and similarly fo r thc bra nch bctween nodes
and we add
@
@
W
-1
6
Y
hus.J
=
-1
1
( -j4.0)
@
Appropriately' subtracting and adding the three change matrices and the original
Y
bus give the new bus admittance matrix for the uncoupled branches
-
j
1
4
.S
j8. 0
Y
hus (new)
=
j8.0
-j1 7.0
j4 .0
j4.0
@
j2.S
jS.O
which agrees with Examrlc 7.1.
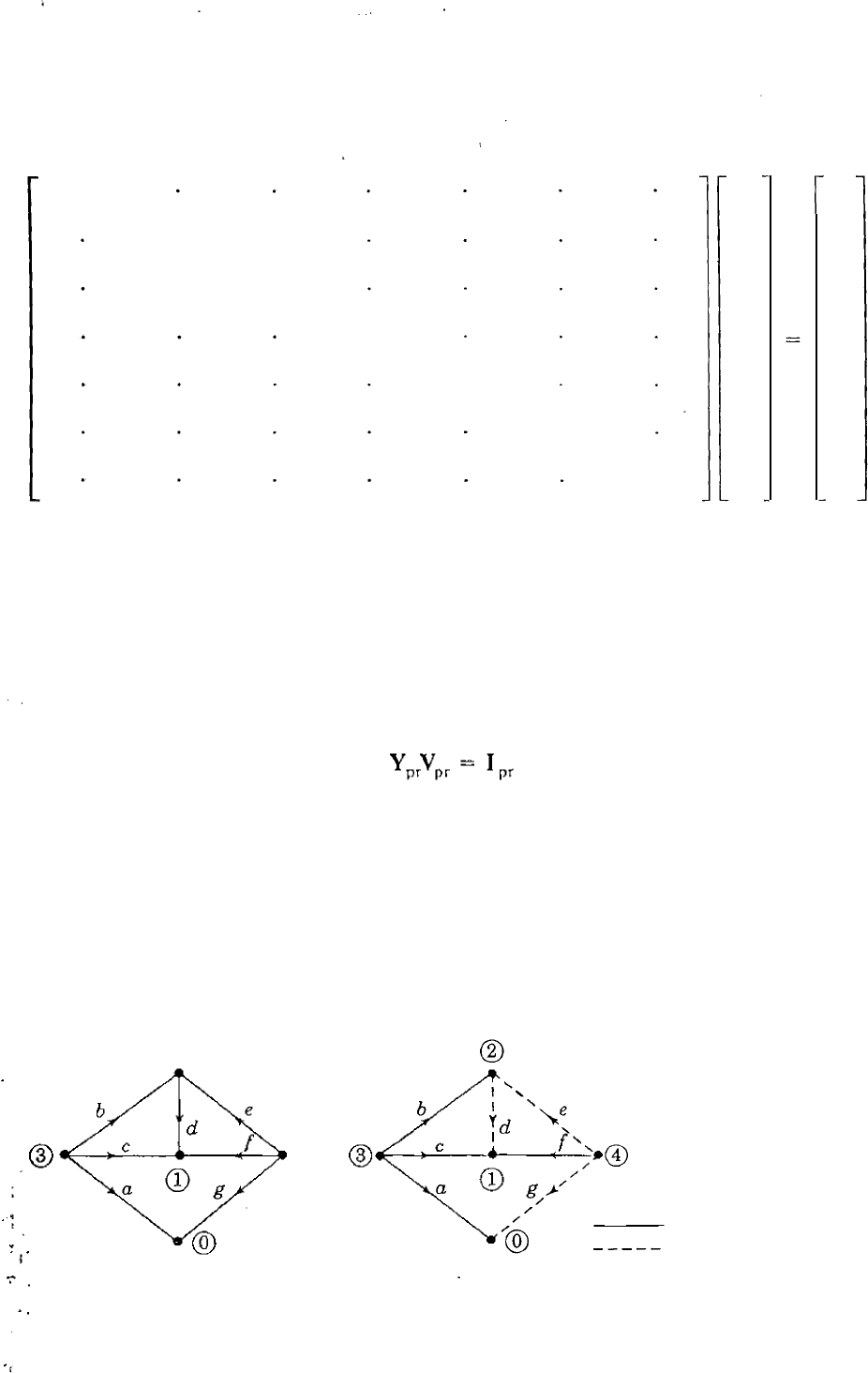
7.5 THE NETWO RK INCIDENCE MATRIX
AND Yh
u
�
@
@
j4.0
j2.S
j4.0
jS .O
-j8.8
0
0
-j8 .
3
In Sees
.
7.1 and 7.2 nodal admittance equations for each branch and mutually
coupled pair of branches are derived independently from those of other branches
in the network. The nodal admittance matrices of the individual branches are
then combined together in order to build
Y h
u
s
of the overall system. Since we
now understand the process, we may proceed to the more formal approach
which treats all the equations of the system simultaneously rather than sepa
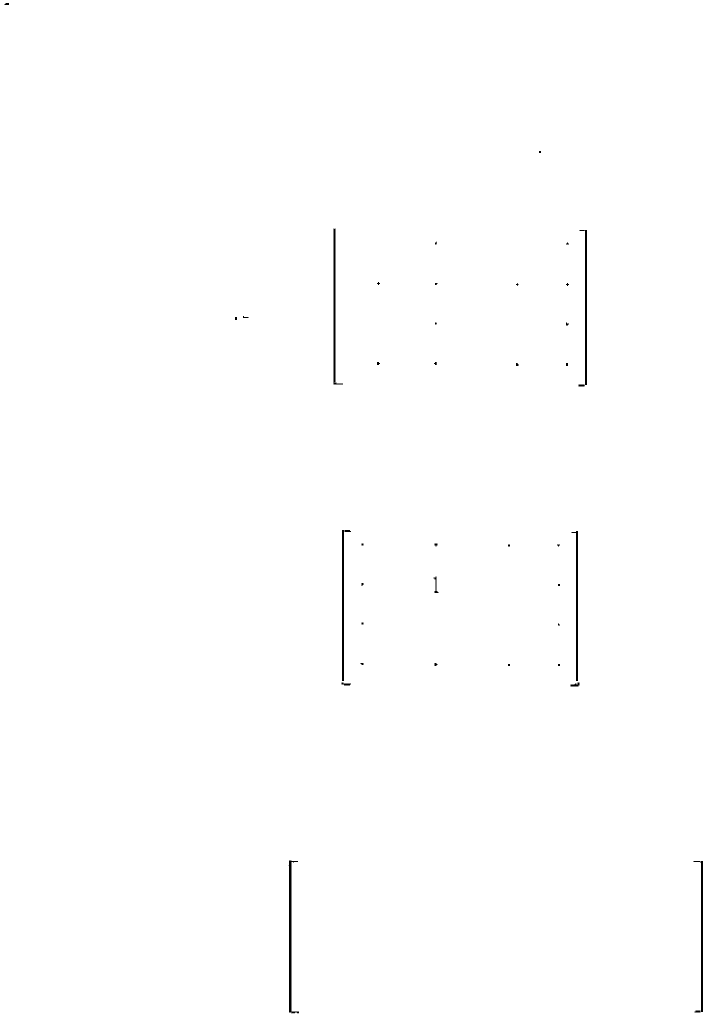
rately. We will use the example system of Fig. 7.11 to establish the general
procedure.
Two of the seven branches in Fig. 7.11 are mutually coupled as shown
.
,
The mutually coupled pair is characterized by Eq. (7.14) and the other ve
- 2008 — 2025 «СтудМед»