Stevenson J. Power system analysis
Подождите немного. Документ загружается.

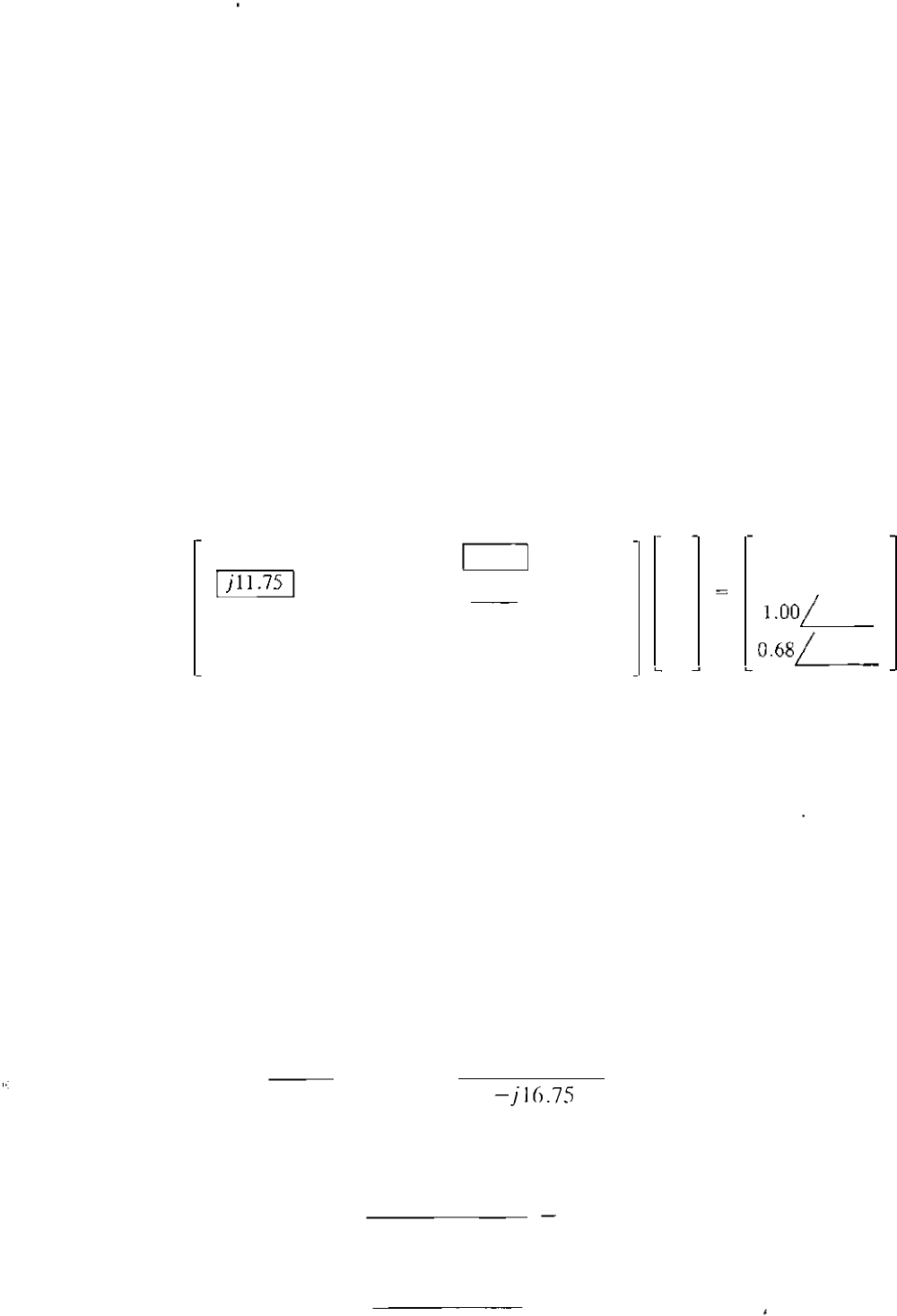
7.6 THE METHOD OF SUCCESSIVE ELIMINA TION
267
back in Eq. (7.61) to obtain a value for V3 • Continuing this process of back
substitution using the values of V3 and � in Eq. (7.56), we obtain V2 and then
solve for V
I
from Eq. (7.47).
Thus, the gaussian-elimination procedure demonstrated here for a four-bus
system provides a systematic means of solving large systems of equations
without having to invert the coecient matrix. This is most desirable when a
larg-scale power system is being analyzed. The following example numerically
illustrates the procedure.
Example 7.7. Using gaussian elimination, solve the nodal equations of Example
7.5 to nd the bus voltages. At each step of the solution hnd the equivalent circuit
of the reduced coeflicient matrix.
Solution. 1n Example 7.5 t he nodal acl mi ttance equations in matr ix form are fo und
to be
W
@
-j16.7S
jl1 .7S
I
j2.S0 ]
j2.S0
V
I
0
- 2008 — 2025 «СтудМед»
