Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists
Подождите немного. Документ загружается.

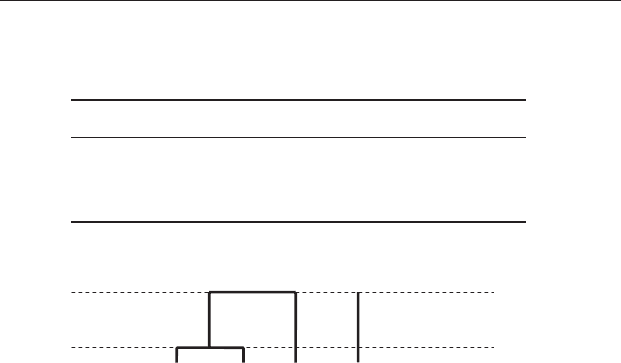
two are now assigned to the same cluster, with an internal dissimilarity of
57.4. This gives two clusters: (A&B&D) and site C (Figure 20.16).
Next, the matrix of dissimilarities is reduced to the one in Table 20.11.
Here, because there are only two sampling units left to compare, the only
dissimilarity necessary to calculate is between (A&B&D) and site C. Here too,
the dissimilarities in the very first matrix (Table 20.9) are averaged. The
calculation is slightly more complex because you need to take the average of
three dissimilarities A–C, B–C and D–C. This is (59.9 + 80.9 + 63.1)/3 = 68.0.
These values for increasing dissimilarity can be used to construct the final
dendogram showing the sites grouped into fewer and few clusters (Figure 20.17).
The dendogram shows a three-cluster solution at 13.3 internal dissimilarity, a
two-category solution at 57.4 internal dissimilarity, and a single-category sol-
ution at 68.0 internal dissimilarity. This result is consistent with the results of the
MDS analysis of the same data in Figure 20.13, which is not surprising.
The advantage of a cluster analysis is that it gives you a quantitative way of
assigningsamplingunitstogroups. For example, from the dendogram in
Figure 20.17 you could suggest that A&D are “in the same group” which is
different from group B and group C. Importantly, however, the groupings
produced by a cluster analysis are unlikely to correspond to “true” categorical
attributes (such as black or white sand grains) given as examples of nominal
ADBC
13.3
57.4
Figure 20.16 Fusion of the first cluster (A&D) and the next most similar (site
B) to give two clusters, (A&D&B) and site C, on the basis of a maximum of
57.4 units of dissimilarity within clusters.
Table 20.10 The reduced matrix of results for the Euclidian
distances between the clusters shown in Figure 20.16.
Sites (A&D) Site B Site C
Sites (A&D) 0
Site B 57.4 0
Site C 61.5 80.9 0
20.17 Q-mode analyses: cluster analysis 293
scale data in Chapter 6. Instead, the categories are based on decisions made
about dissimilarity (or its converse, similarity) which is a continuous and
ratio scale variable. This is an important point. Cluster analysis was primarily
developed for taxonomists – biologists who describe and define animal and
plant species – as a way of helping them make a decision as to whether
individuals should be categorized as the same or different species. Here too,
however, even though the analysis can be used to define clusters it does not
mean these have identified real discontinuities or discrete categories.
In geological applications, cluster analysis has become a commonly used
technique to distinguish and help characterize groups on the basis of many
types of geological data: major, minor, and isotope geochemistries, sediment
particle sizes, drainage basin morphologies, or fossil contents. Cluster
analysis has even been used to group different boulder morphologies and
differentiate geochemical units on Mars. In these applications, results of
cluster analysis are often highly dependent on normalization of the data for
the respective variables, particularly because geological data may lack nor-
mal or log-normal distributions and be strongly skewed or have multiple
modes.
Table 20.11 The matrix of results for the Euclidian distance
between the only possible pair (A&D&B) and site C.
Sites A&D&B Site C
Sites A&D&B 0
Site C 68.0 0
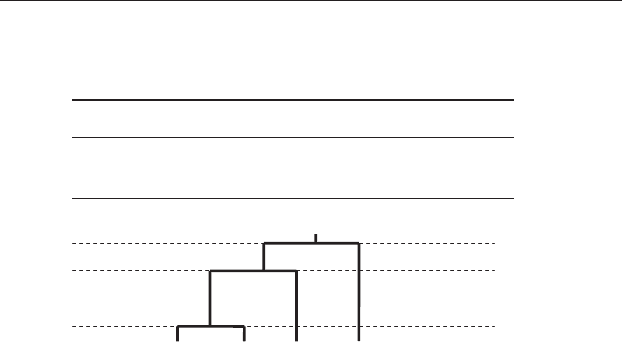
ADBC
13.3
57.4
68.0
Figure 20.17 Dendogram showing sites A, B, C and D hierarchically
arranged in fewer clusters as the amount of dissimilarity allowed within
clusters increases. At 13.3 units of dissimilarity there are three clusters: (A&D),
B and C. These reduce to two clusters: (A&D&B) and C at 57.4 units. Fusion
into only one cluster occurs at 68.0 units of maximum dissimilarity within a
cluster.
294 Introductory concepts of multivariate analysis

20.18 Which multivariate analysis should you use?
The three analyses described in this chapter are all ways of summarizing and
simplifying a multivariate data set so that relationships among sampling
units can be more easily visualized, but they have different applications.
Principal components analysis is useful for data sets where there are few
zero values and you need to know which variables contribute most to
differences among sampling units.
Multidimensional scaling can be used with data sets that contain a lot of
zero values. Most MDS programs do not give an indication of which original
variables contribute to differences among sampling units.
Cluster analysis assigns objects to groups, based on dissimilarity or
similarity, which may help you categorize the sampling units.
This chapter has only described three commonly used multivariate
methods. This is deliberate. First, many earth scientists may never use
multivariate analyses themselves, but will need a conceptual grasp of how
they actually work, so they can evaluate reports that include summary
statistics and conclusions from multivariate data. Second, more powerful
methods of analyzing multivariate data are being developed, but most of
these are derivations of these three “core” methods.
20.19 Questions
(1) Discuss the statement “If there are no correlations within a
multivariate data set then principal components analysis really
is not very much use at all.”
(2) An earth scientist carried out a principal components analysis
and obtained the following eigenvalues for components 1 to 5.
Which components would you use for a graphical display of the
data? Why?
Principal component Eigenvalue Percentage variation
1 3.54 54
2 2.82 23
3 2.64 22
4 0.89 6
5 0.42 5
20.19 Questions 295

(3) What is “stress” in the context of a two-dimensional summary
of the results from a multidimensional scaling analysis?
(4) Why are the “groups” produced by cluster analysis often not
equivalent to true cases of categorical data (such as black versus
white sand grains)?
296 Introductory concepts of multivariate analysis

21 Introductory concepts of
sequence analysis
21.1 Introduction
Geoscientists often have to interpret data that are in the form of a
sequence – an ordered series of observations – that has been measured
over time or space. For example, on a temporal scale you might have data
for sea level that has been repeatedly sampled at the same location over
several months, years, or decades and need to know if the mean has
changed, whether there is a consistent trend, or even repetition of the
same pattern. The analysis of temporal scale data is often called time series
analysis.Onaspatial scale, sequential data might be obtained as a core from
a bore hole drilled down through a sedimentary sequence or a stack of lava
flows. Although such sequences are spatial, they could also be thought of as
temporalbecausedeeperrocksarelikelytobeolder,butdepthandageare
unlikely to be equivalent because the thickness deposited may vary among
years. Nevertheless, the same statistical methods can often be used for both
temporal and spatial sequences.
Data for a sequence can be measured on a ratio, interval scale or ordinal
scale (e.g. the conductivity of well water over several months) or a nominal
scale (e.g. chemical or porosity changes with depth in a stratigraphic
sequence).
Analysis of a sequence might detect a trend (or a lack of it), or reveal
features that may lead to hypotheses about temporal or spatial processes.
Patterns of occurrence within a sequence may also be used as predictors of
conditions of interest. For example, deposits of some minerals (e.g. uranium)
are accompanied by very characteristic modifications of the geochemistry
of surrounding rocks. The resultant alteration haloes are especially charac-
teristic of minerals formed by migrating uranium-rich fluids. It would be
very useful to know that areas of uranium mineralization had a 40%
297

probability of occurring below a particular type of rock showing an alter-
ation halo (e.g. bleaching of initially hematite-rich sandstone).
All of the techniques for sequence analysis described here use statistical
methods explained earlier in this book. We will assume an understanding of
correlation (Chapter 15), regression (Chapter 16) and contingency tables
(Chapter 18 ) to introduce the essential concepts, terminology and techni-
ques of sequence analysis and interpretation.
21.2 Sequences of ratio, interval or ordinal scale data
A sequence of ratio, interval or ordinal scale data measured temporally or
spatially is a bivariate data set with a measured variable (e.g. sea level) and a
sequence variable (e.g. time or distance) giving position within the sequence.
Several things may affect the measured variable. First, there is likely to be
a random component (the “error” discussed in Chapters 10 and 16).
Second, there may be a longer-term upward or downward trend. Third,
there may be a regular repetitive pattern such as the annual summer/winter
fluctuation in temperature, or a longer-term repetition (e.g. climate change)
that is not annual or seasonal. Fourth, part(s) of the sequence may be
consistently higher or lower than the mean. Finally, the value of the
measured variable may be somewhat dependent on the value(s) in previous
parts of the same sequence. A sequence analysis is used in an attempt to
explain as much of this variation as possible in order to characterize a
sequence, test for significant variation over time and perhaps even make
some very cautious predictions.
21.3 Preliminary inspection by graphing
As a first step, it is very helpful to graph the measured variable on the Y axis
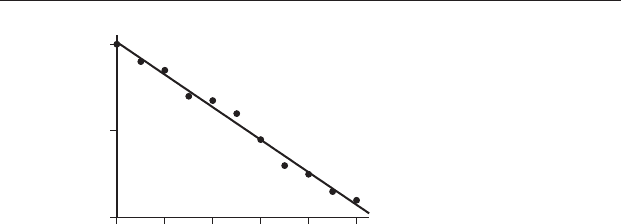
and the sequence variable (e.g. time) on the X axis. For example, Figure 21.1
gives the strength of the magnetic field of the Earth during the past
100 years. Many scientists interpret this decrease in the dipole moment to
be a precursor to a reversal of the Earth’s magnetic poles.
By inspection, the decrease in field strength is approximately linear.
Both variables have been measured on a ratio scale, so the first (and
simplest) model applied to the data could be a linear regression with field
strength (Y) as the dependent variable and time (X) as the independent one
298 Introductory concepts of sequence analysis
(Chapter 16). If the regression line appears to be a good fit to the data and
the assumptions of regression are met, it may be all you need to describe the
sequence and test for a significant change in the measured variable over
time.
Most sequences are more complex than the one in Figure 21.1. Often the
relationship between the measured variable and the sequence variable is not
linear, and there may be similarity or dissimilarity between different parts
of the sequence.
21.4 Detection of within-sequence similarity
and dissimilarity
As a second exploratory step to help establish the features of a sequence, it
is often examined for within-sequence similarity and dissimilarity. As an
example, consider an ice core from a glacier, where the percentage of impur-
ities has been measured at regular intervals down the length of the core. Any
repetition of the same or similar values, or pattern (e.g. a regular cyclic change)
along the length of the core may help understand the processes responsible for
changes within a sequence and can even be used to tentatively predict what
might happen in the future.
One way of detecting repetition is to copy the data from the core, thus
giving two identical sequences. If these two sequences are laid parallel to
each other and side by side, with the beginning of the “top” sequence
aligned with the beginning of the “bottom” one, then each of the
adjacent values in the two sequences will be the same (Figure 21.2(a)).
9
8
7
1900 1920 1940 1960 1980 2000
Date
VADM
Figure 21.1 Strength of the Earth’s magnetic field expressed as the virtual
axis dipole moment (VADM as 10
22
Am
2
) during the past century.
21.4 Within-sequence similarity/dissimilarity 299
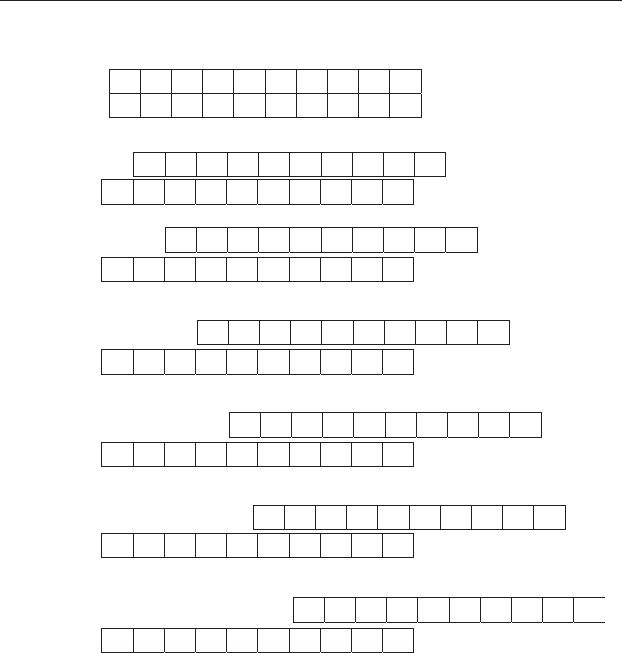
Next, the top sequence is successively shifted to the right, by one
observation at a time. After each shift the overlapping parts of the two
cores are compared to each other to see if they are similar or dissimilar
(Figure 21.2(b–g)). As the two cores are progressively moved past each
(a)
21
21
21 15 10
2 6 15 22 14 9 1
21 15 10
2 6 15 22 14 9 1
21 15 10
2 6 15 22 14 9 1
21 15 10
2 6 15 22 14 9 1
21 15 10
2 6 15 22 14 9 1
21 15 10 2 6 15 22 14 9 1
21 15 10 2 6 15 22 14 9 1
21 15 10 2 6 15 22 14 9 1
21 15 10 2 6 15 22 14 9 1
21 15 10 2 6 15 22 14 9 1
15 10 2 6 15 22 14 9 1
1
9
14
22
15
6
2
2
2
6
6
15
15
22
22
14
14
9
9
1
1
10
10
15
15
15 10
21
21
(b)
(c)
(d)
(e)
(f)
(g)
Figure 21.2 Examination of a sequence, running from left to right with the
most recently recorded value on the right, for internal similarity and
dissimilarity. (a) The sequence of data on percent impurity is copied and placed
alongside itself to give two identical sequences. (b) The top sequence is shifted
by one interval to the right, thereby putting every value in the lower sequence
adjacent to that for the previous interval in the top one, and the overlapping
sections compared. (c)–(g). The process described in (b) is repeated. For the
shift shown at (g), the two sets of four cells in the overlapping section have
similar values, thus indicating a pattern of similarity between different parts of
the sequence. Note also that for the shift in (d), high values in one sequence are
aligned with low values in the other, indicating sections where the pattern in one
is the opposite (and therefore markedly dissimilar) to the other.
300 Introductory concepts of sequence analysis

other, the most recent parts of the bottom core will occur adjacent to
older and older parts of the top one, so if a pattern occurs within a
sequence then the similar or dissimilar sections will, at some stage, lie
side by side (Figure 21.2(g)).
This method is straightforward, but an essential assumption is that
samples have been taken at regular intervals throughout the sequence
(e.g. usually an equal length increment in geological settings). If the intervals
are unequal, then it may be possible to obtain a regular sequence by excluding
some data.
It would be very time consuming to visually inspect the two sequences
every time they were shifted. Furthermore, you need some way of deciding
whether any similarity or dissimilarity is significant or whether it might
only be occurring by chance within a sequence of random numbers. This
can be done by using autocorrelation (which is sometimes called serial
correlation) to test for a relationship, without assuming dependence or
causality. As described above, a sequence is copied to give two identical
ones which are then placed side by side (Figure 21.2(a)). The values
adjacent to each other will be the same, so at this stage the correlation
(Chapter 15) between the variables “sequence 1” and “sequence 2” will
always be 1.0.
Next, sequence 1 is shifted only one interval to the right (Figure 21.2(b)).
This shift is called a lag interval of one (or just a lag of one), and it places
every value within sequence 2 adjacent to the value recorded at the previous
interval in sequence 1. The correlation is recalculated. The process is
repeated several times: the sequence is shifted another interval in the same
direction (therefore giving lag intervals of two, three, four etc.) and the
correlation recalculated each time (Figure 21.2(c)–(g)). The number of lags
that can be used will be limited by the length of a finite sequence, because
every successive shift will reduce the length of the overlapping section
by one.
If there is marked similarity within the sequence then the correlation at
some lag intervals will be strongly positive (e.g. Figure 21.2(g)).
If there is no marked similarity or dissimilarity and only random
variation, the correlation will show some variation but have a mean of zero.
If the pattern at a particular lag in one sequence is the opposite of the
other and therefore markedly dissimilar, the correlation will be strongly
negative (e.g. Figure 21.2(d)).
21.4 Within-sequence similarity/dissimilarity 301

To obtain Pearson’scorrelationcoefficient for a set of bivariate data
(Chapter 15), the means of each variable are separately calculated and used
to convert the two sets of data to their Z scores using the following formulae.
For a population:
Z ¼
X
i
(21:1 copied from 15:1)
and for a sample:
Z ¼
X
i
X
s
(21:2 copied from 15:2)
Importantly, a sequence assessed for autocorrelation is usually treated as a
population because it contains all of the data for that sequence. Therefore,
when calculating Z scores the mean and variance of the entire sequence are
used, not just the sample means and variances for the overlapping sections.
Using Z scores, the Pearson correlation coefficient for a population is:
r ¼
P
N
i¼1
ðZ
xi
Z
yi
Þ
N
(21:3)
For autocorrelation (that compares the measured variable to itself) the
use of Z
x
is inappropriate and Z
y
is used instead:
r ¼
P
N
i¼1
ðZ
yi
Z
yi
Þ
N
(21:4)
Equation (21.4) gives the autocorrelation for a lag of zero, but this will
always be 1.00. As the lag interval increases the number of overlapping
values will decrease so the actual number of values being correlated will be
fewer (Figure 21.2).
To calculate the autocorrelation between different lags of the same
sequence, two modifications to Equation (21.4) are needed.
First, to specify the actual parts of the sequences being compared, the
numerator of Equation (21.4) is changed to that shown in Equation (21.5),
where k is the lag number. This may look complex, but working through the
equation using an example will help. For a lag k = 10 and i = 1, then Z
yi
(which is Z
y(1)
and the first value in the sequence), will be paired with Z
y(i+ k)
(which is Z
y(11)
and the 11th value in the sequence). For the same lag of 10,
when i = 2 the numerator will pair Z
yi
(which is Z
y(2)
) with Z
y(i+ k)
(which is
302 Introductory concepts of sequence analysis
