Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists

Подождите немного. Документ загружается.

assigned to each strip, in a randomized block design with three treatments

and six blocks. Soil in the control treatment was plowed, while soil in the

other two treatments was (a) plowed and mixed with 10 g/kg vermiculite

and (b) 50 g/kg vermiculite. Data for the number of grams of water per

100 grams of topsoil three weeks after the treatments were applied are in

Table 19.6.

For a Friedman test the data are ﬁrst transformed to ranks. These are

assigned within each block and therefore within each row of Table 19.6.

The lowest value in each row is given the rank of “ 1”, the next highest “2”

etc., and the highest rank cannot exceed the number of treatments.

If the treatments are from the same population, the range of ranks (and the

rank sums) for each should also be similar, with any variation due to chance.

If,however,thereisanyeﬀect of either treatment, the ranks and their sums

will also diﬀer. For the example in Table 19.6, the control contains all but two

of the lowest ranks, while treatment B (50 g/kg vermiculite) contains all but

one of the highest.

Next, the total of the squared rank sums is calculated. The size of this total

will depend on the relative size of the rank sums (Box 19.1) with a set of

similar ones giving a smaller total than a set of dissimilar ones.

Finally the following formula is used to calculate the Friedman statistic 



baða þ 1Þ

i¼1

 3bða þ 1Þ (19:7)

where a isthenumberoftreatmentsorgroupsandb is the number of blocks.

This appears complex, but can be split into three components as shown in

equation (19.8) below. The Friedman statistic is obtained by multiplying

components A and B together and then subtracting component C.



baða þ 1Þ



i¼1

 3bða þ 1Þ

ðcomponent AÞðcomponent BÞðcomponent CÞ

(19:8)

Components A and C will increase as sample sizes and the number of

samples increase. If the rank sums are very similar among treatments,

component B will be relatively small so the value of the Friedman statistic

will also be small. As the diﬀerences among the rank sums increase,

component B will increase, thus giving an increasingly larger value of the

19.6 Three or more related samples 263

Friedman statistic. Once this exceeds the critical value above which less than

5% of the most extreme departures from the null hypothesis occur when

samples are taken from the same population, the outcome is considered

statistically signiﬁcant.

This analysis can be up to 95% as powerful as the equivalent two-factor

ANOVA without replication for randomized blocks.

19.6.2 Exact tests and randomization tests for three or more

related samples

The procedures for randomization and exact tests on the ranks of three or

more related samples are extensions of the methods for two independent

samples and do not need to be explained any further.

19.6.3 A posteriori comparisons for three or more related samples

If the Friedman test shows a signiﬁcant diﬀerence among treatments and

the eﬀect is considered ﬁxed, you are likely to want to know which treatments

are signiﬁcantly diﬀerent (see 19.4.3). A posteriori testing can be done and

instructions are given in more advanced texts such as Zar (1996).

19.7 Analyzing ratio, interval or ordinal data that show

gross diﬀerences in variance among treatments and

cannot be satisfactorily transformed

Some data show gross di ﬀerences in variance among treatments that

cannot be improved by transformation and are therefore unsuitable for

parametric or non-p arametric analysis. An exploration geolog ist in Canada

was evaluatin g the economic potential of a circular depression thought to

be an impact c rater. They knew that the large-s cale impact structure at

nearby Sudbur y was associated with valuable copper and nickel deposits,

and that other im pact structures are ex cellent reservoirs for oil and gas.

So they set out to determine if the new locality might a lso be an impact

structure.

One of the key properties of impacted rocks is their high concentration of

platinum group elements. Perhaps the most diagnostic of these is iridium,

which is famously found all over the world in an ash layer that corresponds

264 Further non-parametric tests

to the end of the Cretaceous Period and the extinction of the dinosaurs.

Iridium is not normally present in crustal rocks on the Earth’s surface – it is

usually found only in the metallic cores of diﬀ erentiated planets and in iron

from meteorites. So when an impact from an iron-rich object occurs on

Earth, the iridium vaporizes and is distributed among the impact ejecta in

unusually high concentrations (up to 100 parts per billion). Thus iridium

concentration can be used as a geochemical tracer to indicate that rocks

have experienced an impact event.

The exploration geologist collected 15 core samples from his suspected

new impact site, along with 15 from the Sudbury impact structure. The

concentration of iridium in the two samples of 15 is given in Table 19.7.

It is clear there are gross diﬀerences in the distributions between the two

samples, with one showing bimodality. A solution is to transform the data to

a nominal scale and reclassify both samples into two mutually exclusive

categories of “with iridium” and “no iridium” (Table 19.8) which can be

compared using a test for two or more independent samples of categorical

data (Chapter 18).

Table 19.7 The Ir contents (in parts per billion)

of 15 rocks sampled at Sudbury crater (a classic

impact site) and 15 at a new site with a circular

feature suspected to be an impact crater.

Sudbury New site

10 0

12 1

19.7 Gross diﬀerences in variance 265

19.8 Non-parametric correlation analysis

Correlation analysis was introduced in Chapter 15 as an exploratory tech-

nique used to examine whether two variables are related or vary together.

Importantly, there is no expectation that the numerical value of one variable

can be predicted from the other, nor is it necessary that either variable is

determined by the other.

The parametric test for correlation gives a statistic that varies between

+1.00 and –1.00, with both of these extremes indicating a perfect positive

and negative straight line relationship respectively, while values around

zero show no relationship. Although parametric correlation analysis is

powerful, it can only detect linear relationships and also assumes that both

the X and Y variables are normally distributed. When normality of both

variables cannot be assumed, or the relationship between the two variables

does not appear to be linear and cannot be remedied by transformation,

it is not appropriate to use a parametric test for correlation. The most

commonly used non-parametric test for correlation is Spearman’srank

correlation.

19.8.1 Spearman’s rank correlation

This test is extremely stra ightforward. The two v ariables are r anked

separately, from lowest to highest, and the (parametric) Pearson correla-

tion coeﬃcient calculated for the ranked values. This gives a statistic c alled

Spearman’s rho, which for a population i s symbolized by ρ

and by r

for a

sample.

Spearman’s r

and Pearson’s r will not always be the same for the same set

of data. For Pearson’s r the correlation coeﬃcients of 1.00 or –1.00 were

Table 19.8 Transformation of the ratio data in Table 19.7 to a nominal

scale showing the number of replicates in each sample as the two

mutually exclusive categories of with and without detectable iridium.

Sudbury New site

Number without iridium 0 10

Number with iridium 15 5

266 Further non-parametric tests

900

700

900 800

900

200

400

700

300

200

2.5

800

700

500

400

500

(a)

Raw score Raw scoreRaw scoreRank

Raw score Rank

Rank Rank

(b) (c)

(d)

(e) (f)

1.00

0.80

0.60

0.1

– 1.00

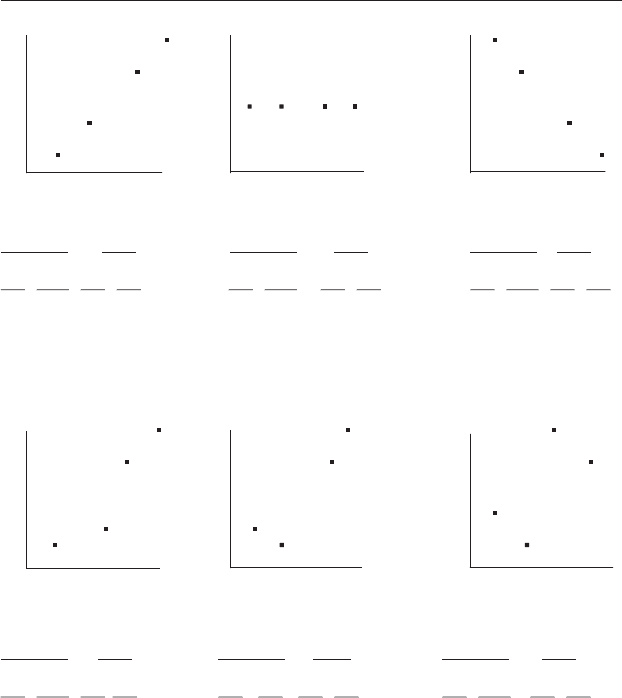
Figure 19.2 Examples of raw scores, ranks and the Spearman rank

correlation coeﬃcient for data with: (a) a perfect positive relationship

(all points lie along a straight line); (b) no relationship; (c) a perfect negative

relationship (all points lie along a straight line); (d) a positive relationship

which is not a straight line but all pairs of bivariate data have the same ranks;

(e) a positive relationship with only half the pairs of bivariate data having

equal ranks; (f) a positive relationship with no pairs of bivariate data having

equal ranks. Note that the value of r

is 1.00 for case (d) even though the raw

data do not show a straight-line relationship.

19.8 Non-parametric correlation analysis 267

only obtained when there was a perfect positive or negative straight-line

relationship between the two variables. In contrast, Spearman’s r

will give a

value of 1.00 or –1.00 whenever the ranks for the two variables are in perfect

agreement or disagreement (Figure 19.2), which occurs in more cases than a

straight-line relationship.

The probability of the value of r

can be obtained by comparing it to the

expected distribution of this statistic and most statistical packages will give

together with its probability.

19.9 Other non-parametric tests

This chapter is only an introduction to some non-parametric tests for two or

more samples of independent and related data. Other non-parametric tests

are described in more specialized but nevertheless extremely well-explained

texts such as Siegel and Castallan (1988).

19.10 Questions

(1) The table below gives summary data for the depth of the water table, in

feet, for a population of 1000 wells. (a) What are the relative frequencies

and cumulative relative frequencies for each depth? (b) For a sample of

100 wells, give a distribution of water table depths that would not be

signiﬁcantly diﬀerent from the population. (c) For another sample of

100 give a distribution of water table depths you would expect to be

signiﬁcantly deeper than the population. (d) What test would be appro-

priate to compare these samples to the known population?

Depth (feet) Number of wells

20–29

150

30–39

300

40–49

140

50–59

110

60–69

70–79

110

80–89

140

90–99

268 Further non-parametric tests

(2) An easy way to understand the process of ranking, and the tests that use

this procedure, is to use a contrived data set. The following two inde-

pendent samples have very similar rank sums. (a) Rank the data across

both samples and calculate the rank sums. (b) Use a statistical package

to run a Mann–Whitney test on the data. Is there a signiﬁcant diﬀerence

between the samples? (c) Now change the data so you would expect a

signiﬁcant diﬀerence between groups. Run the Mann–Whitney test

again. Was the diﬀerence signiﬁcant?

Group 1 Group 2

11 10

12 13

15 14

16 17

19 18

20 21

(3) The following set of data for the percentage of sandstone porosity shows

a gross diﬀerence in distribution between two samples. (a) How might

you compare these two samples? (b) Use your suggested method to test

the hypothesis that the two samples have diﬀerent porosities. Is there a

signiﬁcant diﬀerence?

Sample 1: 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 5, 2

Sample 2: 1, 1, 1, 1, 1, 1, 10, 11, 11, 11, 12, 12, 13, 13, 13, 13, 14, 14, 15,

17, 18, 18, 19

19.10 Questions 269

20 Introductory concepts of

multivariate analysis

20.1 Introduction

So far, all the analyses discussed in this book have been for either univariate

or bivariate data. Often, however, earth scientists need to analyze samples of

multivariate data – where more than two variables are measured on each

sampling or experimental unit – because univariate or bivariate data do

not give enough detail to realistically describe the material or the environ-

ment being investigated.

For example, a large ore body may contain several diﬀerent metals, and

the concentrations of each of these may vary considerably within it. It would

be useful to have a good estimate of this variation because some parts of the

deposit may be particularly worth mining, others may not be worth mining

at all, or certain parts may have to be mined and processed in diﬀerent ways.

Data for only one or two metals (e.g. copper and silver) are unlikely to be

suﬃcient to estimate the full variation in composition and value within a

deposit that also includes lead and zinc.

Samples on which multivariate data have been measured are often diﬃ-

cult to compare with one another because there are so many variables. In

contrast, samples where only univariate data are available can easily be

visualized and compared (e.g. by summary statistics such as the mean and

standard error). Bivariate data can be displayed on a two-dimensional

graph, with one axis for each variable. Even data for three variables can be

displayed in a three-dimensional graph. But as soon as you have four or

more variables, the visualization of these in a multidimensional space and

comparison among samples becomes increasingly diﬃcult. For example,

Table 20.1 gives data for the concentrations of ﬁve metals at four sites.

Although this is only a small data set, it is diﬃcult to assess which sites are

most similar or dissimilar. (Incidentally, you may be thinking this is a

270

very poor sampling design, because data are only given for one sampling

unit at each site. This is true, but here we are presenting a simpliﬁed data set

for clarity.)

Earth scientists need ways of simplifying and summarizing multivari-

ate data to compare samples. Because univariate data are so easy to visual-

ize, the comparison among the four sites in Table 20.1 would be greatly

simpliﬁed if the data for the ﬁve metals could somehow be reduced to a

single statistic or measure. Multivariate methods do this by reducing the

complexity of the data sets while retaining as much information as possible

about each sample. The following explanations are simpliﬁed and concep-

tual, but they do describe how these methods work.

20.2 Simplifying and summarizing multivariate data

The methods for simplifying and comparing samples of multivariate data

can be divided into two groups.

(a) The ﬁrst group of analyses works on the variables themselves. They

reduce the number of variables by identifying the ones that have the

most inﬂuence upon the observed diﬀerences among sampling units

so that relationships among the units can be summarized and visual-

ized more easily. These “variable-oriented” methods are often called

R- mode analyses.

(b) The second group of analyses works on the sampling units. They often

summarize the multivariate data by calculating a single measure, or

statistic, that helps to quantify diﬀerences among sampling units.

These “sample-oriented” methods are often called Q-mode analyses.

Table 20.1 The concentrations of ﬁve metals at four sites (A–D). From these raw

data, it is diﬃcult to evaluate which sites are most similar or dissimilar.

Metal Site A Site B Site C Site D

Copper 12 43 26 21

Silver 11 40 28 19

Lead 46 63 26 21

Gold 32 5 19 7

Zinc 6 40 21 38

20.2 Simplifying and summarizing multivariate data 271

This chapter will describe an example of an R- mode analysis, followed by

two Q-mode ones.

20.3 An R-mode analysis: principal components analysis

Principal components analysis (PCA) (which is called “principal compo-

nent analysis” in some texts) is one of the oldest multivariate techniques.

The mathematical procedure of PCA is complex and uses matrix algebra,

but the concept of how PCA works is very easy to understand. The following

explanation only assumes an understanding of the correlation between two

variables (Chapter 15).

If you have a set of data where you have measured several variables on a

set of sampling units (e.g. a number of sites or cores), which for PCA are

often called objects, it is very diﬃcult to compare them when you have data

for more than three variables (e.g. the data in Table 20.1).

Quite often, however, a set of multivariate data shows a lot of redun-

dancy – that is, two or more variables are highly correlated with each other.

For example, if you look at the data in Table 20.1, it is apparent that the

concentrations of copper, silver and zinc are positively correlated (when

there are relatively high concentrations of copper there are also relatively

high concentrations of silver and zinc and vice versa). Furthermore, the

concentrations of copper, silver and zinc are also correlated with gold, but

we have deliberately made these correlations negative (when there are

relatively high concentrations of gold, there are relatively low concentra-

tions of copper, silver and zinc and vice versa) because negative correlations

are just as important as positive ones.

These correlations are an example of redundancy within the data set –

because four of the ﬁve variables are well-correlated, and knowing which

correlations are negative and which are positive, you really only need the

data for one of these variables to describe diﬀerences among the sites.

Therefore, you could reduce the data for these four metals down to only one

(copper, silver, gold or zinc) plus lead in Table 20.2 with little loss of

information about the sites.

A principal components analysis uses such cases of redundancy to reduce

the number of variables in a data set, although it does not exclude variables.

Instead, PCA identiﬁes variables that are highly correlated with each other

and combines these to construct a reduced set of new variables that still

272 Introductory concepts of multivariate analysis