Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists

Подождите немного. Документ загружается.

means will be the same or close to the grand mean, so the F ratio will be close

to 1.0. The test for whether the slope of a regression line is signiﬁcantly

diﬀerent to the horizontal line showing



Y is done in a similar way.

First, the regression line will be tilted from the line showing



Y because of

the variation explained by the regression equation (regression plus

error).

Second, each of the points in the scatter plot will be displaced upwards or

downwards from the regression line because of the remaining variation

(error only).

It is easy to calculate the sums of squares and mean squares for these two

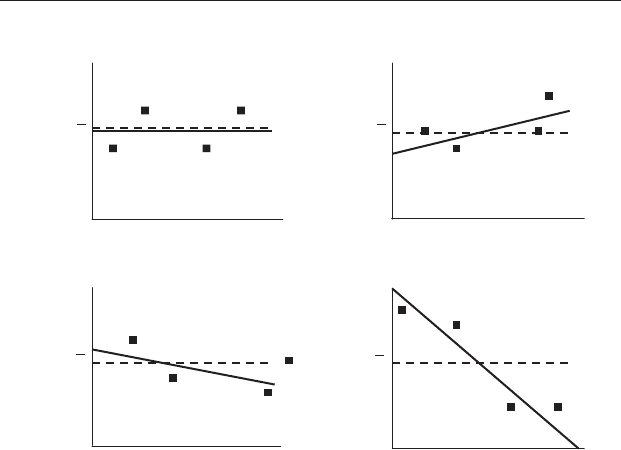
separate sources of variation. Figure 16.7 shows scatter plots for two sets of

data. The ﬁrst regression line (16.7(a)) has a large positive slope and the

second (16.7(b)) has a slope much closer to zero. The horizontal line on

each graph shows



Y. Here you need to think about the vertical displacement

(a)

(b)

(c)

(d)

Figure 16.6 A regression line always crosses the line showing



Y. (a) If the

slope is exactly zero the regression line will be indistinguishable from the

horizontal line showing



Y. Samples from a population where the slope β is

zero will nevertheless be expected to include cases with small (b) positive and

then the regression line will be strongly tilted from the line showing



Y.A

negative slope is shown as an example.

16.5 Testing the signiﬁcance 213

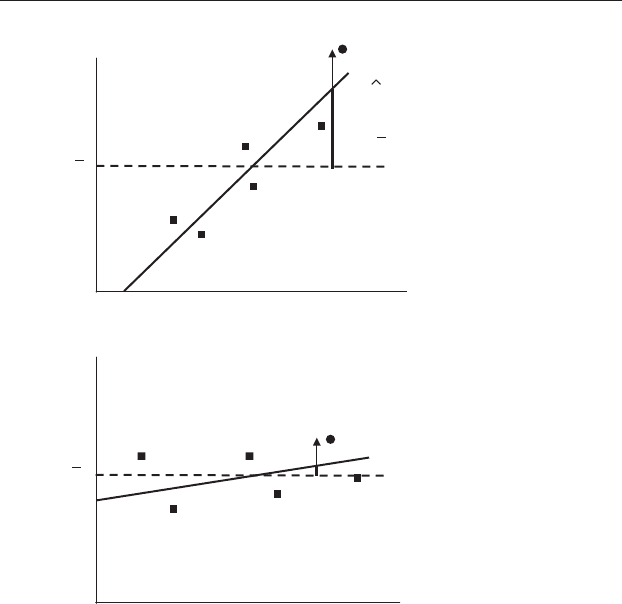
of each point from the line showing



Y. To illustrate this, the point at the top

far right of each scatter plot in Figure 16.7 has been identiﬁed by a circle

instead of a square. The vertical arrow running up from



Y to each of the

circled points ðY 



YÞ indicates the total variation or displacement of that

X, Y

(a)

X,Y

(b)

Figure 16.7 (a) The diagonal solid line shows the regression through a

scatter plot of six points, and the dashed horizontal line shows



Y. The vertical

arrow shows the displacement of one point, symbolized by a circle instead of a

square, from



Y. The distance between the point and the Y average Y 



YðÞis

the total variation, which can be partitioned into variation explained by the

regression line and unexplained variation or error. The heavy part of the

vertical line

Y 





shows the displacement explained by the regression line

(regression plus error) and the remainder Y 



is unexplained variation

(error). Note that (a) when the slope is large, the explained component is also

large; and (b) when the slope is close to zero, then the explained component is

very small.

214 Linear regression

point from



Y. This distance can be partitioned into the two sources of

variation mentioned above.

The ﬁrst is the amount of displacement explained by the regression line

(which is aﬀected by both the regression plus error) and is the distance

Y 



YÞ shown by the heavy part of the vertical arrow in Figure 16.7.

The second is the distance ðY 

YÞshown by the lighter vertical part of the

arrow in Figure 16.7.Thisisunexplained variation or error and often called

the residual variation because it is the amount of variation remaining

between the data points and

Y that cannot be explained by the regression line.

This gives a way of calculating an F ratio that indicates how much of the

variation can be accounted for by the regression.

First, you can calculate the sum of squares for the variation explained by

the regression line by squaring the vertical distance between the regression

line and



Y for each point ð

Y 



YÞ and adding these together. Dividing this

sum of squares by the appropriate number of degrees of freedom will give

the mean square due to explained variation (regression plus error).

Second, you can calculate the sum of squares for the unexplained varia-

tion by squaring the vertical distance between each point and the regression

line ðY 

YÞ and adding these together. Dividing this sum of squares by the

appropriate number of degrees of freedom will give the mean square due to

unexplained variation or “error.”

At this stage, you have sums of squares and mean squares for two sources

of variation that will be very familiar to you from the explanation of one-

factor ANOVA in Chapter 10:

(a) The variation explained by the regression line (regression plus

error).

(b) The unexplained residual variation (error only).

Therefore, to get an F ratio that shows the proportion of the variation

explained by the regression line compared to the unexplained variation

due to error, you divide the mean square for (a) by the mean square

for (b).

1;n2

MS regression

MS residual

(16:9)

If the regression line has a slope close to zero (Figure 16.6(a)) both the

numerator and denominator of Equation (16.9) will be similar, so the

16.5 Testing the signiﬁcance 215

value of the F statistic will be approximately 1.0. As the slope of the line

increases (Figure 16.6(b), (c) and (d)), the numerator of Equation (16.9) will

become larger, so the value of F will also increase. As F increases, the

probability that the data have been taken from a population where the

slope of the regression line, β, is zero will decrease and will eventually be

less than 0.05. Most statistical packages will calculate the F statistic and give

the probability. There is an explanation for the number of degrees of free-

dom for the F ratio in Box 16.2.

Box 16.2 A note on the number of degrees of freedom in an

ANOVA of the slope of the regression line

The example in Section 16.6 includes an ANOVA table with an F statistic

and probability for the signiﬁcance of the slope of the regression line.

Note that the “regression” mean square, which is equivalent to the

“treatment” mean square in a single-factor ANOVA, has only one degree

of freedom. This is the case for any regression analysis, despite the

sample size used for the analysis. In contrast, for a single-factor

ANOVA the number of degrees of freedom is one less than the number

of treatments. This diﬀerence needs explaining.

Forasingle-factorANOVA,allbutoneofthetreatmentmeansarefree

to vary, but the value of the “ﬁnal” one is constrained because the grand

mean is a set value. Therefore, the number of degrees of freedom for the

treatment mean square is always one less than the number of treatments. In

contrast, for any regression line every value of

Y must (by deﬁnition) lie on

the line. For a regression line of known slope, once the ﬁrst value of

Y has

been plotted the remainder are no longer free to vary because they must lie

on the line, so the regression mean square has only one degree of freedom.

The degrees of freedom for error in a single-factor ANOVA are the

sum of one less than the number within each of the treatments. Because a

degree of freedom is lost for every treatment, if there are a total of n

replicates (the sum of the replicates in all treatments) and k treatments,

the error degrees of freedom are n − k. In contrast, the degrees of freedom

for the residual (error) variation in a regression analysis are always n − 2.

This is because a regression line, which only ever has one degree of

freedom, is always only equivalent to an experiment with two treatments.

216 Linear regression

16.5.2 Testing whether the intercept of the regression line

is signiﬁcantly diﬀerent to zero

The value for the intercept a calculated from a sample is only an estimate of

the population statistic α. Consequently, a positive or negative value of a

might be obtained in a sample from a population where α is zero. The

standard deviation of the points scattered around the regression line can be

used to calculate the 95% conﬁdence interval for a, and a single-sample t test

can be used to compare the value of a to zero or any other expected value.

Once again, most statistical packages include a test to determine if a diﬀers

signiﬁcantly from zero.

16.5.3 The coeﬃcient of determination r

The coeﬃcient of determination, symbolized by r

, is a statistic that shows

the proportion of the total variation of the values of Y from the average



that is explained by the regression line. It is the regression sum of squares

divided by the total sum of squares:

Sum of squares explained by the regressionððaÞ aboveÞ

Total sum of squaresððaÞþðbÞ aboveÞ

(16:10)

which will only ever be a number from zero to 1.0. If the points all lie along the

regression line and it has a slope that is diﬀerent from zero, the unexplained

component (quantity (b)) will be zero and r

will be 1. If the explained sum of

squares is small in relation to the unexplained, r

will be a small number.

16.6 An example: school cancellations and snow

In places at high latitudes, heavy snowfalls are the dream of every young

student, because they bring the possibility of school closures (called “snow

days”), not to mention sledding, hot chocolate and additional sleep! A school

administrator looking for a way to predict the number of school closures on any

day in the city of St Paul, Minnesota hypothesized that it would be related to

the amount of snow that had fallen during the previous 24 hours. To test this,

they examined data from 10 snowfalls. These bivariate data for snowfall

(in cm) and the number of school closures on the following day are given in

Table 16.1.

16.6 An example: school cancellations and snow 217

From a regression analysis of these data a statistical package will give

values for the equation for the regression line, plus a test of the hypotheses

that the intercept, a, and slope, b are from a population where α and β are

zero. The output will be similar in format to Table 16.2.

From the results in Table 16.2 the equation for the regression line is

school closures = 5.773 + 0.853 × snowfall. The slope is signiﬁcantly diﬀer-

ent to zero (in this case it is positive) and the intercept is also signiﬁcantly

diﬀerent to zero. You could use the regression equation to predict the

number of school closures based on any snowfall between 3 and 30 cm.

Table 16.1 Data for 24-hour snowfall and the number

of school closure days for each of 10 snowfalls.

Snowfall (cm) School closures

613

916

12 14

15 18

18 23

21 20

24 32

27 29

30 28

Table 16.2 An example of the table of results from a regression analysis. The value

of the intercept a (5.733) is given in the ﬁrst row, labeled “(Constant)” under the

heading “Value”. The slope b (0.853) is given in the second row (labeled as the

independent variable “Snowfall”) under the heading “Value.” The ﬁnal two columns

give the results of t tests comparing a and b to zero. These show the intercept, a,is

signiﬁcantly diﬀerent to zero (P = 0.035) and the slope b is also signiﬁcantly diﬀerent

to zero (P < 0.001). The signiﬁcant value of the intercept suggests that there may be

other reasons for school closures (e.g. ice storms, frozen pipes), or perhaps the

regression model is not very accurate.

Model Value Std error t Signiﬁcance

Constant 5.733 2.265 2.531 0.035

Snowfall 0.853 0.122 7.006 0.001

218 Linear regression

Most statistical packages will give an ANOVA of the slope. For the data in

Table 16.1 there is a signiﬁcant relationship between school closures and

snowfall (Table 16.3).

Finally, the value of r

is also given. Sometimes there are two values: r

which is the statistic for the sample and a value called “Adjusted” r

, which is

an estimate for the population from which the sample has been taken. The r

value is usually the one reported in the results of the regression. For the

example above you would get the following values:

r ¼ 0:927; r

¼ 0:860; adjusted r

¼ 0:842

This shows that 86% of the variation in school closures with snowfall can be

predicted by the regression line.

16.7 Predicting a value of Y from a value of X

Because the regression line has the average slope through a set of scattered

points, the predicted value of Y is only the average expected for a given value

of X. If the r

value is 1.0, the value of Y will be predicted without error,

because all the data points will lie on the regression line. Usually, however,

the points will be scattered around the line. More advanced texts describe

how you can calculate the 95% conﬁdence interval for a value of Y and thus

predict its likely range.

16.8 Predicting a value of X from a value of Y

Often you might want to estimate a value of the independent variable X

from the dependent variable Y. Here is an example. Many elements absorb

energy of a very speciﬁc wavelength because the movement of electrons or

Table 16.3 An example of the results of an analysis of the slope of a regression. The

signiﬁcant F ratio shows the slope is signiﬁcantly diﬀerent to zero.

Sum of squares df Mean square F Signiﬁcance

Regression 539.648 1 539.648 49.086 0.000

Residual 87.952 8 10.994

Total 627.600 9

16.8 Predicting a value of X from a value of Y 219

neutrons from one energy level to another within atoms is related to the

vibrational modes of crystal lattices. Therefore, the amount of energy

absorbed at that wavelength is dependent on the concentration of the

element present in a sample. Here it is tempting to designate the concen-

tration of the element as the dependent variable and absorption at the

independent one and use regression in order to estimate the concentration

of the element present. This is inappropriate because concentration of an

element does not depend on the amount of energy absorbed or given oﬀ,so

one of the assumptions of regression would be violated.

Predicting X from Y can be done by rearranging the regression equation

for any point from:

¼ a þ bX

(16:11)

to:

 a

(16:12)

but here too the 95% conﬁdence interval around the estimated value of X

must also be calculated because the measurement of Y is likely to include

some error. Methods for doing this are given in more advanced texts.

16.9 The danger of extrapolating beyond the range

of data available

Although regression analysis draws a line of best ﬁt through a set of data,

it is dangerous to make predictions beyond the measured range of X.

Figure 16.8 illustrates that a predicted regression line may not be a correct

estimation of the value of Y outside this range.

16.10 Assumptions of linear regression analysis

The procedure for linear regression analysis described in this chapter is

often described as a Model I regression, and makes several assumptions.

First, the values of Y are assumed to be from a population of values that

are normally and evenly distributed about the regression line, with no

gross heteroscedasticity. One easy way to check for this is to plot a graph

showing the residuals. For each data point its vertical displacement on the Y

220 Linear regression

axis either above or below the ﬁtted regression line is the amount of residual

variation that cannot be explained by the regression line, as described in

Section 16.5.1. The residuals are calculated by subtraction (Table 16.4) and

plotted on the Y axis, against the values of X for each point and will always

give a plot where the regression line is re-expressed as horizontal line with

an intercept of zero.

If the original data points are uniformly scattered about the original

regression line, the scatter plot of the residuals will be evenly dispersed in

a band above and below zero (Figure 16.9). If there is heteroscedasticity the

band will vary in width as X increases or decreases. Most statistical packages

will give a plot of the residuals for a set of bivariate data.

(a)

0 2

4 6

(b)

Figure 16.8 It is risky to use a regression line to extrapolate values of Y

beyond the measured range of X. The regression line (a) based on the data for

values of X ranging from 1 to 5 does not necessarily give an accurate prediction

(b) of the values of Y beyond that range. A classic example of such behavior is

found in plots of the geothermal gradient of the Earth’s interior. At shallow

depths, there is generally a linear increase in temperature of ~20 K/km depth,

depending on location, but the rate increases as you go deeper into the mantle.

16.10 Assumptions of linear regression analysis 221

Second, it is assumed the independent variable X is measured without

error. This is often diﬃcult and many texts note that X should be measured

with little error. For example, levels of an independent variable determined

by the experimenter, such as the relative % humidity, are usually

measured with very little error indeed. In contrast, variables such as the

depth of snowfall from a windy blizzard, or the in situ temperature of a

violently erupting magma, are likely to be measured with a great deal of

error. When the dependent variable is subject to error, a diﬀerent analysis

called Model II regression is appropriate. Again, this is described in more

advanced texts.

Third, it is assumed that the dependent variable is determined by the

independent variable. This was discussed in Section 16.2.

Fourth, the relationship between X and Y is assumed to be linear and it is

important to be conﬁdent of this before carrying out the analysis. A scatter

plot of the data should be drawn to look for any obvious departures from

linearity. In some cases it may be possible to transform the Y variable

Table 16.4 Original data and ﬁtted regression line of Y = 10.8 + 0.9X. The residual for

each point is its vertical displacement from the regression line. Each residual is

plotted on the Y axis against the original value of X for that point to give a graph

showing the spread of the points about a line of zero slope and intercept.

Original data

Calculated value

Y from

regression equation

Data for the plot of residuals

Value of X (from

original data)

Value of Y

ðY 

YÞ

1 13 11.7 1 1.3

3 12 13.5 3 − 1.5

4 14 14.4 4 − 0.4

5 17 15.3 5 1.7

6 17 16.2 6 0.8

7 15 17.1 7 − 2.1

8 17 18.0 8 − 1.0

9 21 18.9 9 2.1

10 20 19.8 10 0.2

11 19 20.7 11 − 1.7

12 21 21.6 12 − 0.6

14 25 23.4 14 1.6

222 Linear regression