Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists

Подождите немного. Документ загружается.

The results of a two-factor ANOVA without replication will include the

sums of squares and mean squares for Factor A, Factor B, and error,

together with the F ratios and probabilities for Factors A and B. For the

example given above the results of the analysis are in Table 14.2.

14.3 A posteriori comparison of means after a two-factor

ANOVA without replication

If a two-factor ANOVA without replication shows a signiﬁcant eﬀect of a

ﬁxed treatment factor (e.g. the three temperatures that are speciﬁcally

compared in Section 14.2), then you are likely to want to know which

treatments appear to be from the same or diﬀerent populations.

The procedure for a posteriori testing is a modiﬁcation of the formula for

a single-factor ANOVA, except that because there is no directly estimated

value for error, the MS error for interaction plus error (estimated by

subtraction) is used as the best estimate of this. For a Tukey test, each factor

is examined separately using the formula:

q ¼



X



SEM

(14:1 copied from 11:1)

with the standard error of the mean estimated from:

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

MS error

(14:2 copied from 11:3)

where the MS error is the one calculated by subtraction in the ANOVA table

(see Table 14.2) and n is the number of data within each group (for example,

there are three values within each of the three pressures when temperature is

ignored and vice versa).

Table 14.2 Results of a two-factor ANOVA without replication on the data in

Table 14.1. There is a signiﬁcant eﬀect of temperature but no signiﬁcant eﬀect of

pressure on the growth of feldspar phenocrysts.

Source of Variation Sum of Squares df Mean square FP

P (MPa) 4.222 2 2.111 0.864 0.488

T (°C) 4070.222 2 2035.111 835.545 0.000

Error 9.778 4 2.444

Total 4084.222 8

14.3 A posteriori testing 183

14.4 Randomized blocks

Experiments done in environments where there is considerable spatial

variation (e.g. a 20-acre mining lease) have to be replicated, but often

spatial variation is so great that it may obscure any eﬀect of treatment if

replicates were simply assigned at random within that area. One solution is

to distribute replicates of each treatment fairly evenly across a landscape.

This is often done by setting out a two-dimensional array, with the area

subdivided into a series of strips, called blocks, with every treatment

represented in each. Often only one replicate is available in each block but

these data can be analyzed as a two-factor ANOVA without replication,

with blocks as a random factor and treatments as a ﬁxed or random factor.

This is called a randomized block design and gives a way of separating the

eﬀects of location and treatment.

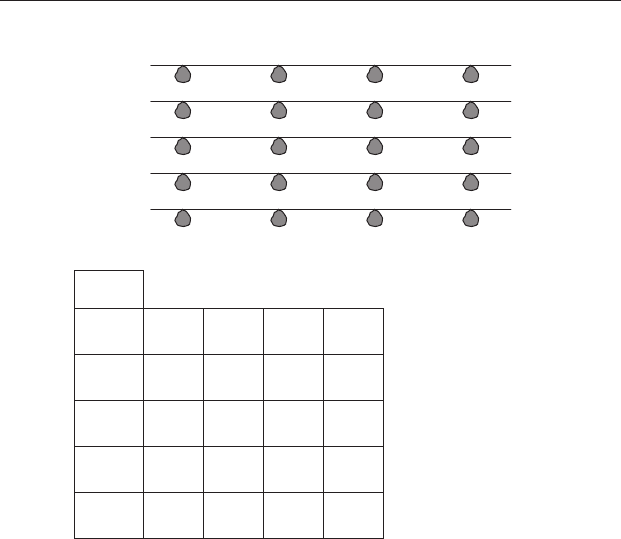
Here is an example. Pearls (which mainly consist of calcium carbonate)

are usually grown by placing oysters in ﬁne-mesh catch bags attached to

chains hanging down at regular intervals from a series of taut horizontal

subsurface longlines running parallel to each other (Figure 14.6(a)). An

aquacultural scientist hypothesized that removal of marine parasites from

the oysters would increase the proportion that produced marketable pearls.

Unfortunately, factors including water depth and temperature, wind expo-

sure, light levels, turbidity and tidal currents may vary from chain to chain

and longline to longline. If you simply used an experimental design with

replicates of each anti-parasite treatment allocated at random to the array

you are likely to get a lot of variation among replicates of the same

treatment.

For a randomized block design, a set of ﬁve parallel longlines (called

blocks 1–5) was established. Four bags, each containing 100 oysters, were

suspended at regular intervals from every longline and one replicate of the

four treatments was assigned at random within each. After six months the

number of oysters with pearls was counted in every bag, thus giving only a

single value at each point in the array (Figure 14.6(b)).

The results from this design can be analyzed as a two-factor

ANOVA without replication, using treatments as the ﬁrst factor and

blocks as the second, thereby subdividing the variation into two

components in order to isolate the eﬀect of treatment from any spatial

variation.

184 More complex ANOVAs

14.5 Nested ANOVA as a special case of a single-factor ANOVA

An experimental design that compares the means of two or more levels of

the same factor (e.g. diﬀerent levels of salinity or diﬀerent compositions)

can be analyzed by a single-factor ANOVA, as described in Chapter 10.

Sometimes, however, researchers do an experiment with two or more levels

of a particular factor, but also have two or more subgroups nested within

each level. Here is an example from the contaminated landﬁll ﬁrst men-

tioned in Chapter 2. The idea is that mixing the heavy-metal-contaminated

soils with apatite group minerals will make the metals bind with the apatite

instead of the soil, thereby preventing them from leaching into

groundwater.

Line 1

Line 2

Line 3

Line 4

Line 5

(a)

Block

number

(b)

Figure 14.6 A randomized block design. (a) Aerial view of a typical

rectangular array used to grow pearl oysters. Five horizontal longlines are run

parallel to each other and bags of 100 oysters (ﬁlled symbols) are suspended

from four chains attached at regular intervals to the longlines. (b) Representation

of the array shown in (a) as a 5 block × 4 column grid. One replicate of each

treatment (A–D) is assigned at random to a bag within each (longline) block.

14.5 Nested ANOVA 185

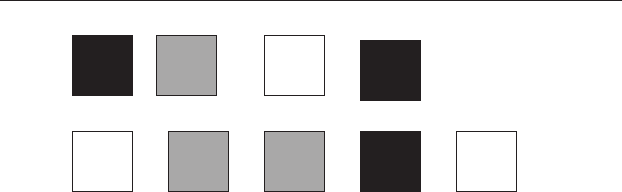
Large-scale experiments in hazardous waste remediation are often con-

strained by the number of test sites available to the researcher. For example,

only nine large test plots at diﬀerent sites within a municipality were

available for an investigation of the eﬀects of chlorapatite vs. ﬂuorapatite

treatments on the lead content of groundwater run-oﬀ from each site. Three

plots were allocated at random to each of these two mineral treatments and

the remaining three plots were used as a control. After six months a sample

containing twelve replicates of groundwater run-oﬀ from each area was

analyzed for lead content.

This is called a nested or hierarchical design. Three plots are nested

within each treatment (Figure 14.7).

This design is not appropriate for analysis using a single-factor ANOVA

with type of treatment (the apatites) as the factor and the response within

each treatment as the number of replicates, because this ignores the pres-

ence of the plots that may contribute to the variation within the experiment.

You may also be thinking that the design appears pseudoreplicated in that

the real level of replication within each treatment is the number of plots

rather than the twelve water replicates taken from within each plot. This is

true and the nested analysis described below takes this into account.

This design is also unsuitable for analysis as a two-factor ANOVA with

mineral treatment as the ﬁrst factor and plots as the second, because the

three plots are simply random subgroups nested within each treatment,

which do not intentionally contain diﬀerent treatment levels of a second

factor. For example, the ﬁrst plot in treatment 1 does not share an exclusive

property with the ﬁrst plot in treatments 2 and 3 (Table 14.3).

Plot A Plot B

Plot C

Plot D

Plot E

Plot F

Plot G Plot H

Plot I

Figure 14.7 Example of a nested or hierarchical design. There are three

diﬀerent treatments, and three plots are nested within each treatment. Open

boxes indicate the control (no apatite treatment), grey boxes treatment 1

(chlorapatite) and black boxes treatment 2 (ﬂuorapatite).

186 More complex ANOVAs

When one factor (e.g. Factor B) is nested within another (e.g. Factor A) it

is often written as Factor B(Factor A). For the nested design above, where

Factor A is the type of apatite used for the treatment and Factor B is the

plots, the following will contribute to the lead content of the groundwater:

Lead in groundwater ¼ Factor A þ Factor BðFactor AÞþerror

This is the same as Equation (10.1) for a single-factor ANOVA apart from an

additional source of variation from the plots nested within each type of apatite

treatment. There is no interaction term because the design is not orthogonal.

A nested ANOVA isolates the eﬀects of treatments and subgroups within

these treatments and gives an F ratio for both factors.

14.6 A pictorial explanation of a nested ANOVA

For simplicity the following example has two treatments and two plots nested

within each treatment, with only four groundwater replicates measured in

Table 14.3 A hierarchical design should not be analyzed as an independent factor

design. (a) Correct hierarchical plan for the nested experimental design described in

Figure 14.7, and (b) incorrect orthogonal two-factor plan because the plots do not

contain diﬀerent levels of a second factor.

(a) A hierarchical design has one factor nested within the other. The plots have been

chosen at random and are nested within each treatment.

No treatment (control) Chlorapatite Fluorapatite

Plot C Plot E Plot I Plot B Plot F Plot G Plot A Plot D Plot H

(b) Incorrect format of the nested design shown above in (a) as a fully orthogonal

design. There is nothing exclusively shared within any of the rows of plots across

treatments so it is incorrect to treat the three rows as three diﬀerent levels of the

factor “plot.”

Treatment

Plot None (control) Chlorapatite Fluorapatite

First within each treatment 12 replicates 12 replicates 12 replicates

(Plot C) (Plot B) (Plot A)

Second within each treatment 12 replicates 12 replicates 12 replicates

(Plot E) (Plot F) (Plot D)

Third within each treatment 12 replicates 12 replicates 12 replicates

(Plot I) (Plot G) (Plot H)

14.6 A pictorial explanation of a nested ANOVA 187

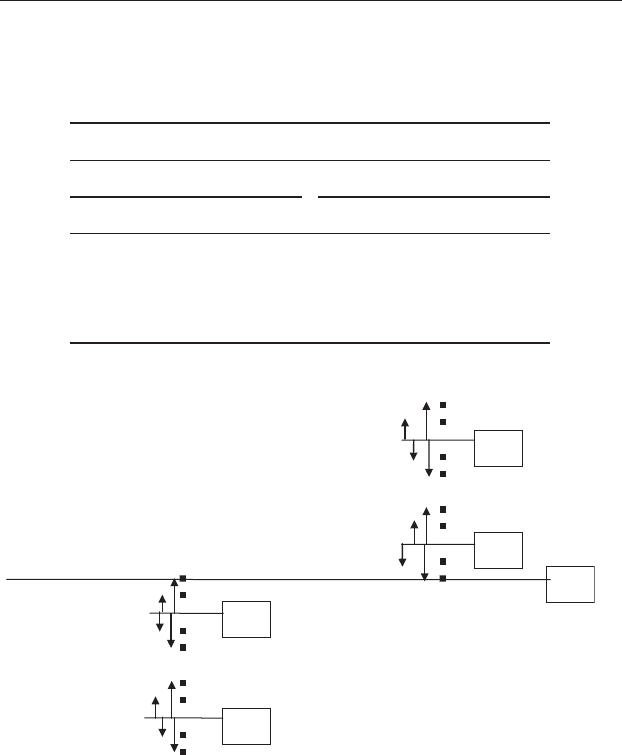
each plot. The data are in Table 14.4. The type of treatment (chlorapatite vs.

ﬂuorapatite) is Factor A and the plots are Factor B(A). Figure 14.8 shows the

data for each of the four groups in Table 14.4 graphed as four separate cells,

including each cell mean and the grand mean.

Lead content (ppm)

chlorapatite

fluora

atite

120

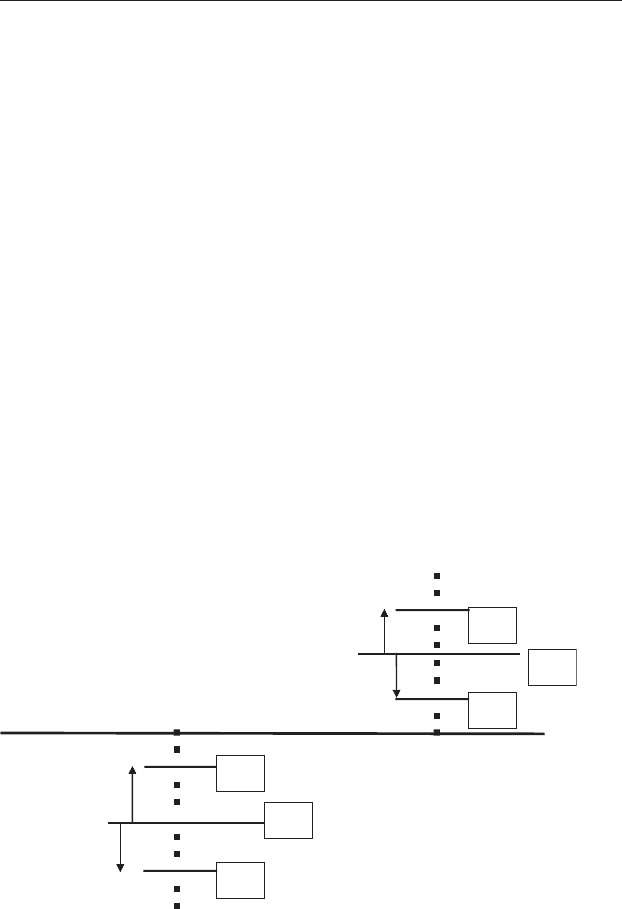
Figure 14.8 Arrows show the displacement of each replicate from its cell

mean, which is the variation due to error only. The number of degrees of

freedom is the sum of one less than the number within each of the cells. In this

example there are 12 degrees of freedom.

Table 14.4 Data for the lead content (in ppm) of groundwater

tested three months after treatment with (a) chlorapatite and

(b) ﬂuorapatite. Two plots are nested within each treatment.

Treatment

chlorapatite ﬂuorapatite

Plot 1 Plot 2 Plot 3 Plot 4

30 60 80 110

35 65 85 115

45 75 95 125

50 80 100 130

188 More complex ANOVAs

First, error is estimated. The value for each replicate is displaced from its

cell mean by error only (Figure 14.8). The sum of squares for error is

obtained by squaring each displacement and adding these together. This

quantity is divided by the appropriate degrees of freedom (the sum of one

less than the number of replicates within each of the cells) to give the mean

square for error.

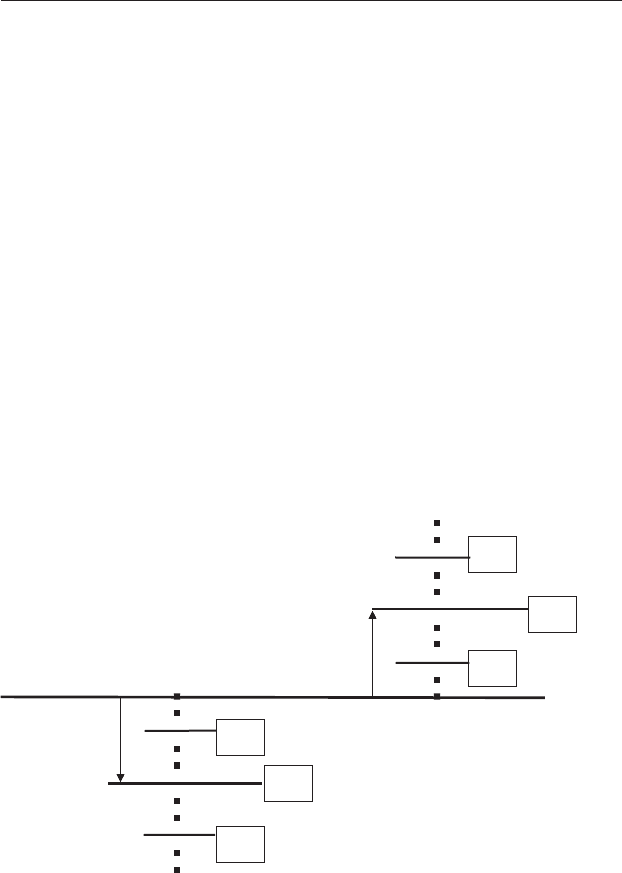
Second, the subgroups (in this case the plots) are ignored and new means

are calculated by combining all of the replicates within each treatment (in

this case the type of apatite used) (Figure 14.9). This will give the eﬀect of

treatment, but for a nested ANOVA each treatment mean will be displaced

from the grand mean because of the eﬀect of treatment plus the subgroups

nested within each treatment, plus error.

This seems inconsistent with the explanation given for an orthogonal

two-factor ANOVA where ignoring a factor (e.g. Factor B) removed it as a

source of variation, allowing the eﬀect of the other (e.g. Factor A) to be

estimated. For a two-factor orthogonal design, all levels of Factor A are

Lead content (ppm)

chlora

atite

fluorapatite

120

105

Figure 14.9 Estimation of the eﬀects of Factor A (treatment). The

displacement of each combined treatment mean for Factor A from the grand

mean shown by the arrows is caused by the average eﬀects of that treatment,

plus plots nested within each treatment, plus error. The number of degrees of

freedom will be one less than the number of treatments, so in this example

with two treatments there is one degree of freedom.

14.6 A pictorial explanation of a nested ANOVA 189

present within every level of Factor B and vice versa, so each of the two

factors can be ignored in turn and the eﬀect of each factor separately

estimated. For a nested design, however, the eﬀects of Factor B (the sub-

groups) cannot be excluded in this way because diﬀerent subgroups (here

diﬀerent plots) are present and may contribute very diﬀerent amounts of

variation within each of the levels of Factor A.

The displacements of each treatment mean from the grand mean are

squared, multiplied by the number of replicates within their respective

treatment and added together to give the sum of squares for Factor A,

which will include treatment plus subgroups(treatment) plus error. The

number of degrees of freedom is one less than the number of treatments and

dividing the sum of squares by this number will give the mean square for

Factor A (i.e. treatment plus subgroups(treatment) plus error).

Third, a mean is also calculated for Factor B(A) which is the variation

contributed by each subgroup (in this case each plot) (Figure 14.10). Each

subgroup mean will only be displaced from its respective treatment mean by

the eﬀect of the subgroups plus error. The displacements are squared,

multiplied by the number of replicates within their respective subgroups

Lead content (ppm)

chlorapatite

fluora

atite

120

105

Figure 14.10 Estimation of the eﬀect of Factor B(A). The displacement of

each cell mean from its treatment mean is shown by each arrow and is caused

by the average eﬀect of that subgroup (each plot) plus error. The number of

degrees of freedom will be the sum of one less than the number of plots within

each treatment. In this example there are two degrees of freedom.

190 More complex ANOVAs

and added together to give the Factor B(A) sum of squares. The number of

degrees of freedom will be the sum of one less than the number of subgroups

within each treatment. Dividing the sum of squares by this number will give

the mean square for Factor B(A) (i.e. subgroups + error).

The procedures shown in Figures 14.8 to 14.10 give three separate sums

of squares and mean squares:

(a) Factor A: treatment + subgroups(treatment) + error (Figure 14.9)

(b) Factor B(A): subgroups(treatment) + error (Figure 14.10)

and no other mean squares are needed to isolate the eﬀects of the treatments

from the subgroups nested within each treatment.

First, to isolate the eﬀect of treatment only, the MS for treatment +

subgroups(treatment) + error is divided by the MS for subgroups(treat-

ment) + error. Second, to isolate the variation due to subgroups(treatment),

the MS for subgroups(treatment) + error is divided by the MS error

(Table 14.5).

In the example shown in Figures 14.8 to 14.10, the F ratio for the eﬀect of

Factor A will only have one and two degrees of freedom, despite the fact that

the experiment used 16 measurements of lead in groundwater. This is

appropriate because the level of replication for this comparison is the

plots rather than the groundwater replicates taken from within each plot.

Most statistical packages will do a nested ANOVA and the results will be

in a similar format to Table 14.6, which gives the results for the data in

Table 14.4. If the treatment factor is ﬁxed and signiﬁcant you are likely to

want to carry out a posteriori testing to examine which treatment means are

signiﬁcantly diﬀerent. The Tukey test ( Equation (14.1)) can be used, but

Table 14.5 The appropriate division and components of each mean square term

used to estimate the eﬀ ect of each factor when Factor B is nested within Factor A.

Source of variation Calculation of F ratio Components of each mean square

Factor A (treatment)

Mean square for Factor A

Means square for B(A)

Factor AþFactor B(A) + error

Factor B(A) + error

Factor B(A)

Mean square for B(A)

Mean square error

Factor B(A) + error

Mean square error

14.6 A pictorial explanation of a nested ANOVA 191

when comparing among treatments the appropriate “MS error” to use in

Equation (14.3) is the MS for subgroups (treatments) instead of the error.

We suggest you use a more advanced text (e.g. Sokal and Rohlf, 1995 or Zar,

1996) if you need to do a posteriori testing after a nested ANOVA.

This example is the simplest case of a nested or hierarchical design. More

complex designs can include several levels of nesting, and nested factors in

combination with two- and higher-factor ANOVAs. If you need to use more

complex designs it is important to read an advanced text or talk to a

statistician before doing the experiment.

14.7 A ﬁnal comment on ANOVA: this book is only an

introduction

Even though this book has ﬁve chapters about analysis of variance, it is only

an introduction to an enormous and diverse topic. There are far more

complex ANOVA models, including those for analyzing repeated measures

on the same experimental or sampling unit over time, several variables

measured on the same unit, and designs with several factors that include

nesting. Hopefully the introduction developed here will make it easier for

you to understand more complex designs described in advanced texts!

14.8 Questions

(1) The table below gives the concentration of total polycyclic aromatic

hydrocarbons (PAHs) in three benthic sediment cores taken 3 km, 2 km

and 1 km from an oil reﬁnery situated on the edge of an estuary. (a)

Analyze the data as a two-factor ANOVA without replication, using

Table 14.6 Results of a nested ANOVA on the data in Table 14.4. Note that the

F ratio for the treatment (type of apatite) has been obtained by dividing the MS for

type of apatite by the MS for plot.

Source of variation Sum of squares df Mean square FP

Apatite type 10000.0 1 10000.0 5.556 0.143

Plot(Apatite) 3600.0 2 1800.0 21.600 0.000

Error 1000.0 12 83.3

192 More complex ANOVAs