Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists

Подождите немного. Документ загружается.

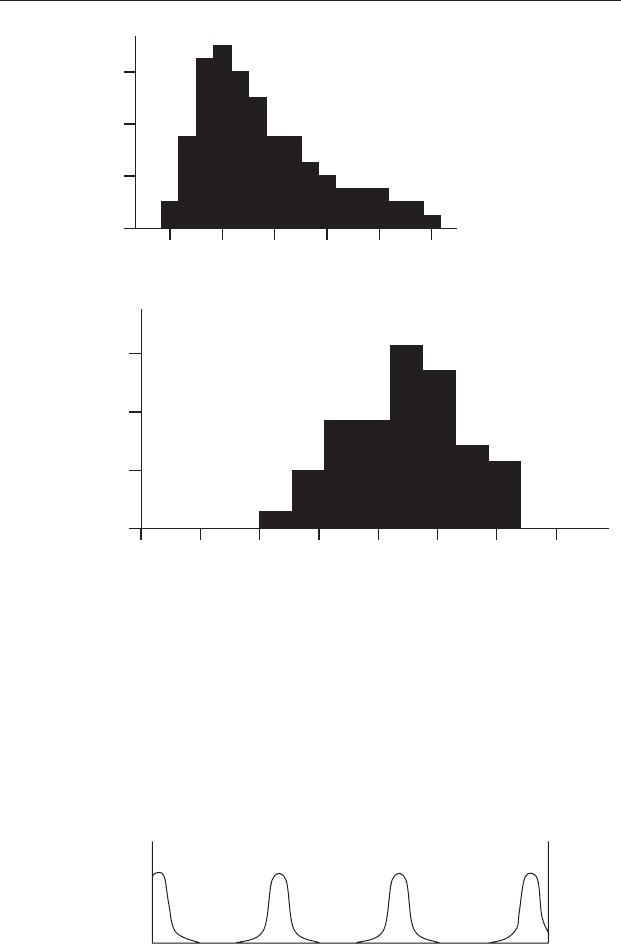
(a)

Number of sections

Number of bubbles per section

6 9 12 15 18

(b)

arithm of the number of bubbles

er section

Number of sections

0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4

Figure 13.4 The eﬀect of logarithmic transformation on data for the

number of bubbles measured on 1 cm

thin sections of volcanic rock. The

X axis shows the number of bubbles per section and the Y axis shows the

number of thin sections measured that contained each number of bubbles.

(a) The data show a pronounced positive skew before transformation. (b)

After transformation to the log

. Note that the distribution in (b) is far

more symmetrical than (a).

Frequency

0 50 100

Percenta

Figure 13.5 Restriction of the normal distribution for percentage data when

the mean is close to zero or 100%.

13.6 Are transformations legitimate? 173

(e.g. earthquake magnitude on the Richter scale vs. energy released, crystal

population density vs. crystal size) are logarithms, squares or cubes. The

apparently linear pH scale is actually logarithmic – a pH of 4 indicates a ten-

fold diﬀerence from pH 5 and a 100-fold diﬀerence from pH 6. Therefore, in

many cases it is actually more appropriate to transform the data so they

reﬂect the underlying relationship.

Importantly, if you transform a set of data, you also need to transform

your null and alternate hypotheses. For example, if you were to hypothesize

that “the steepness of river banks is not related to river basin size” but

carried out a logarithmic transformation on your data before analysis, your

original hypothesis would also have to be transformed to “the steepness of

river banks is not related to the logarithm of river basin size”.

13.7 Tests for heteroscedasticity

There are several tests designed to examine whether two or more samples

appear to have come from populations with the same variance. As men-

tioned earlier, if you are only interested in whether the data are suitable for a

parametric analysis, the general rule that the ratio of the largest variance to

the smallest should not exceed 4 : 1 can be used. If this ratio is greater, it may

be useful to examine the data and see where the diﬀerences occur because it

may be possible to transform the data so that a parametric analysis can

be done.

If, instead, you are interested in testing an hypothesis about the variance

of two or more samples, you can use the Levene test, which also gives an F

ratio. Remember, however, that a signiﬁcant result for the Levene test may

not mean the data are unsuitable for analysis by ANOVA, which is quite

robust to heteroscedasticity.

Levene’s original test calculates the absolute diﬀerence between each

replicate and its treatment mean and then does a one-factor ANOVA on

these diﬀerences. The absolute diﬀerence is the diﬀerence between any two

numbers expressed as a positive value. (For example, the diﬀerence between

6 and 3 is –3, while the diﬀerence between 3 and 6 is +3, but the absolute

diﬀerence in both cases is +3.)

Figures 13.6 and 13.7 are a pictorial explanation of the Levene test. Two

cases are shown, using the data on apatite abundance in sandstones that

were ﬁrst described in Section 11.3.3.

174 Important assumptions of ANOVA

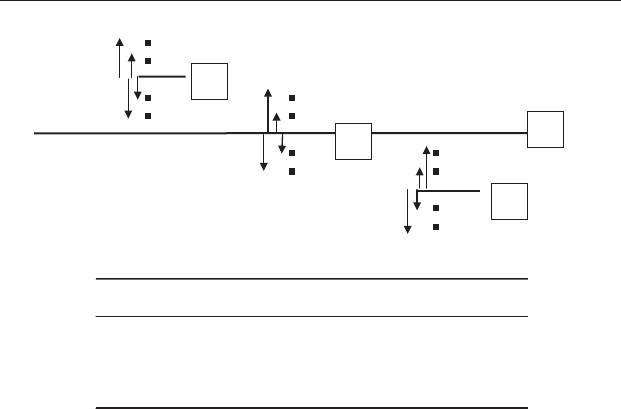
First, if the variances within all treatments are similar, then the set of

absolute diﬀerences between the replicates and their sample means will

also be similar for each treatment. For example, Figure 13.6 shows the

absolute diﬀ erences for three samples that all have the same variance.

Note that the means of the absolute diﬀerences in 13.6(b) are the same,

even though the treatment means in 13.6(a) are not. A one-factor

ANOVA comparing the means of the absolute diﬀerences will not be

signiﬁcant.

Second, if the variances diﬀer among treatments (Figure 13. 7(a))then

so will the values of the absolute diﬀere nce s (Figure 13.7(b)). Note that

the set of absolute diﬀerences for Darcy has a mean that is much larger

thantheothertwo.Asingle-factorANOVAcomparingthesemeansis

(b)

Darcy Runcan Alinda

(a)

Figure 13.6 The Levene test examines whether two or more variances are

likely to have come from the same population by doing a single-factor

ANOVA on the absolute diﬀerences between the replicates and their

treatment means or cell means. (a) Arrows show the diﬀerence between

each replicate and its treatment mean. Note that some diﬀerences are

positive and some are negative. (b) The absolute diﬀerences are listed

under each treatment. Every value of the absolute diﬀerence between each

replicate and its sample mean will be positive. In this case the means of

the absolute diﬀerences are the same for each treatment and a single-factor

ANOVA comparing these will not be signiﬁcant, thereby indicating the

variances are homoscedastic.

13.7 Tests for heteroscedasticity 175

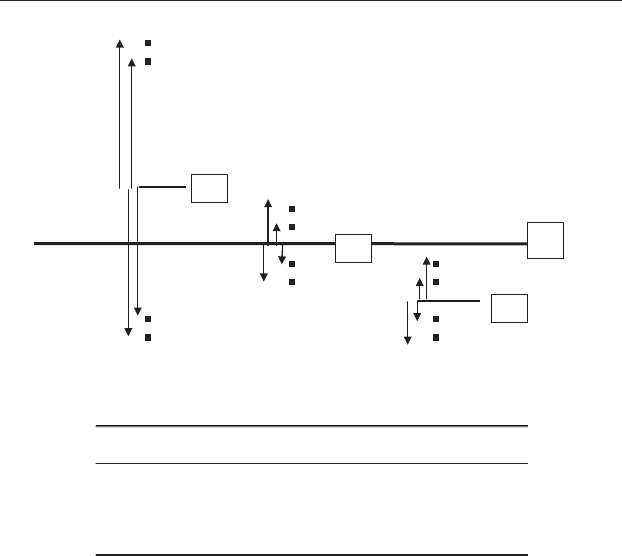
likely to be signiﬁcant. The Levene test is available in most statistical

packages.

13.8 Questions

(1) Why can a transformation be useful when analyzing data with para-

metric tests, especially ANOVA?

(2) You have been given the following set of data for apatite abundance in

sandstones at four outcrops. (a) Do the data require transformation

before running a single-factor ANOVA comparing the four locations?

What transformation would you recommend?

(b)

Darcy Runcan Alinda

(a)

Figure 13.7 An example of the Levene test where there is heteroscedasticity.

(a) Arrows show the diﬀerence between each replicate and its sample mean.

(b) The absolute diﬀerences between each replicate and its sample mean are

listed under each treatment. Because the absolute diﬀerences for Darcy are

much greater than the other two treatments, a single-factor ANOVA

comparing the means of the values in (b) will show the variances are

signiﬁcantly heteroscedastic.

176 Important assumptions of ANOVA

Darlinghurst Glebe Newtown Kiama

15 4 2 7

9249

12 3 3 6

18 1 5 10

13.8 Questions 177

14 Two-factor analysis of variance

without replication, and nested

analysis of variance

14.1 Introduction

This chapter describes two slightly more complex ANOVA models often

used by earth scientists, but an understanding of these is not essential if you

are reading this book as an introduction to geostatistics. If, however, you

need to use more complex analyses then the explanations given here for

two-factor ANOVA without replication and nested ANOVA are straight-

forward extensions of the pictorial descriptions in Chapters 10 and 12 and

will help with many of the ANOVA models used to analyze more complex

designs.

14.2 Two-factor ANOVA without replication

This is a special case of the two-factor ANOVA described in Chapter 12.

Sometimes an orthogonal experiment with two independent factors has to

be done without replication because there is a shortage of sampling units or

the experimental treatments are very expensive. The simplest case of

ANOVA without replication is a two-factor design. You cannot do a single-

factor ANOVA without replication.

Here is an example of a two-factor design without replication. Oil

geologists often drill cores to determine the extent of an oil-rich shale

deposit. Time and ﬁnancial constraints usually mean only one core is

taken every kilometer or so away from the suspected location of the deposit.

Often oil content also varies with depth, and these data are extremely

important for evaluation of the oil ﬁeld, but you can only aﬀord to log a

few sections (at speciﬁc depths) of each core. Therefore, a design where only

one core is taken every kilometer is orthogonal but unreplicated

(Figure 14.1) and care must be taken to avoid confusing variation within

178

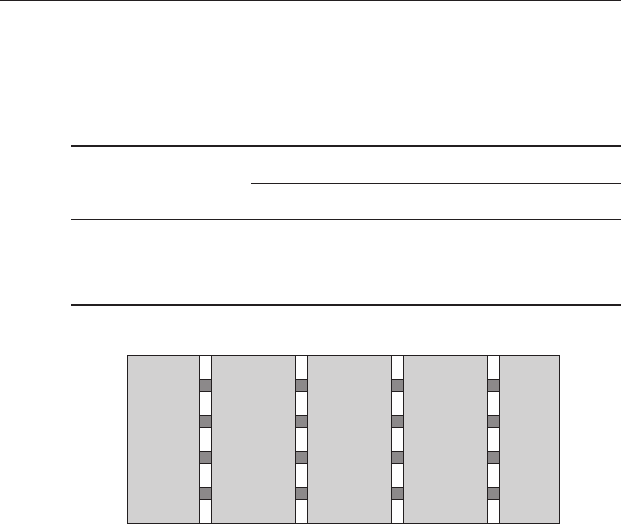
each core with any variation among drill holes at diﬀerent locations.

An analogous situation is also frequently encountered in environmental

geochemistry, where cores are often drilled at diﬀerent distances from a

hazardous waste site to assess the extent (and depth) of contamination.

Another example is given in Table 14.1, which shows data for an experi-

ment to test the eﬀ ects of pressure and temperature on the growth of

feldspar crystals. Pressures of 50 and 100 MPa were being evaluated,

together with a control treatment (0.1 MPa, which is ambient room pres-

sure), for their eﬀect in combination with three diﬀerent temperatures. The

experiments are diﬃcult and time-consuming, so only one replicate at each

of these nine combinations of temperature and pressure could be run, giving

a two-factor orthogonal design without replication.

This causes a problem. There is no way to directly estimate error from the

dispersion of replicates around their respective cell means (as was done for a

single-factor ANOVA in Chapter 10 and a two-factor ANOVA with

Table 14.1 The length of feldspar phenocrysts (in μm) for a crystallization

experiment with nine diﬀerent combinations of pressure and temperature.

All replicates were initially identical compositions. Only one replicate is

available for each combination of the two treatments.

Pressure (MPa)

Temperature (

C) 100 50 0.1

700 81 76 79

800 45 46 45

900 28 27 27

Depth 1

Depth 2

Depth 3

Depth 4

Hole 1

Hole 2

Hole 3 Hole 4

Figure 14.1 When only one core is taken at each location and only one log

(sampling unit) is available at each depth (dark squares) the sampling design is

orthogonal but unreplicated because only one datum is available for each

combination of drill hole and depth.

14.2 Two-factor ANOVA without replication 179

replication in Chapter 12) because there is only one value in each treatment

combination, which will always be the same as the cell mean. A two-factor

ANOVA without replication uses a diﬀerent way of estimating error, which

has to assume there is no interaction between the factors. Figures 14.2 to

14.5 give a pictorial explanation of how a two-factor ANOVA without

replication estimates three sources of variation and uses these to isolate

the eﬀects of the two factors. The data in Table 14.1 are graphed in

Figure 14.2.

First, the total variation within the experiment is estimated. Each point

will be displaced from the grand mean by the eﬀects of Factor A, Factor B,

any interaction and error. These distances can be squared and summed to

give the sum of squares for the total variation in the experiment, with

degrees of freedom that are one less than the number of experimental

subjects.

Second, the eﬀect of Factor A is estimated by ignoring Factor B and

calculating a new mean for each of the levels within Factor A. The displace-

ment of each treatment mean from the grand mean will be caused by the

average eﬀect of Factor A plus error (Figure 14.4). Each of these displace-

ments is squared, multiplied by the number of replicates within each treat-

ment and added together to give the sum of squares for Factor A. The

number of degrees of freedom is one less than the number of treatments,

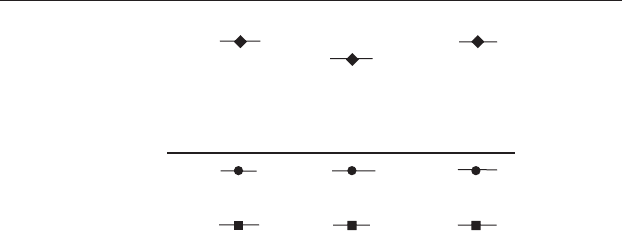
Length

(µm)

100 MPa

50 MPa Control (0.1 MPa)

Grand mean

Figure 14.2 Feldspar phenocryst size in crystallization experiments for nine

combinations of three diﬀerent pressures and temperatures. There is only one

replicate within each treatment combination. The length of each crystal is

shown as a symbol: ♦ = 700 °C, ● = 800 °C and ■ = 900 °C. The heavy

horizontal line shows the grand mean and the nine shorter horizontal lines

show each mean.

180 More complex ANOVAs

and dividing the sum of squares by this value will give the mean square for

Factor A.

Finally, the eﬀect of Factor B is estimated by ignoring Factor A and

calculating a new mean for each treatment level of Factor B. The displace-

ment of each treatment mean from the grand mean will be caused by the

eﬀect of Factor B plus error ( Figure 14.5). Here too, the displacements are

squared, multiplied by the number of replicates within each treatment, and

added together to give the sum of squares for Factor B. The number of

degrees of freedom is one less than the number of treatments, and dividing

by this value will give the mean square for Factor B.

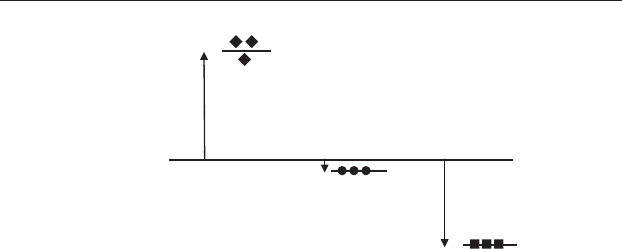
Length

(µm)

Grand mean

100 MPa

50 MPa

Control (0.1 MPa)

Figure 14.3 The total variation within the feldspar crystallization

experiment. The heavy horizontal line indicates the grand mean and the nine

shorter horizontal lines indicate each cell mean. The displacement of each

point from the grand mean (arrows) will be caused by the total variation

within the experiment.

Length

(µm)

Grand mean

100 MPa

50 MPa

Control (0.1 MPa)

Figure 14.4 Estimation of the eﬀect of Factor A. The displacement of each

treatment mean from the grand mean (arrows) will be caused by the eﬀect of

Factor A (here pressure) plus error.

14.2 Two-factor ANOVA without replication 181

At this stage you have estimates for the following sources of variation:

(a) The total variation in the experiment (the combined eﬀects of Factor

A, Factor B, A × B and error) (Figure 14.3)

(b) The eﬀects of Factor A (pressure + error) (Figure 14.4)

Because there is only one replicate within each treatment combination,

there is no way to separately estimate error. Therefore, unlike a two-factor

ANOVA with replication, it is not possible to estimate the sum of squares

for the eﬀect of any interaction by subtracting the sums of squares for Factor

A, Factor B and error from the total variation.

Two-factor ANOVA without replication does the next best thing. The

sums of squares and degrees of freedom in an ANOVA are additive (e.g. in

Chapter 10 it was explained how the total sum of squares and total degrees

of freedom in a single-factor ANOVA were the sums of those for the sums

of squares for Factor A and for error). Therefore, by subtracting the

sums of squares for Factor A plus Factor B from the total variation, you

are left with the sum of squares for t he remaining variation in the experi-

ment, which will include error and any eﬀect of interaction. This sum of

squares, which is the only possible estimate of error, is divided by the

remaining degrees of freedom to give the best available estimate of the

mean square for error. If there is an interaction the mean square will be

inﬂated, but this is unavoidable and undetectable if you do a two- factor

ANOVA without replication.

Length

(µm)

Grand mean

700 °C

800

°C

900

°C

Figure 14.5 Estimation of the eﬀect of Factor B. The displacement of each

treatment mean from the grand mean (arrows) will be caused by the eﬀect of

Factor B (here temperature) plus error.

182 More complex ANOVAs