Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists

Подождите немного. Документ загружается.

(see Chapter 13) to give a linear relationship and proceed with a regression

analysis on the transformed data.

16.11 Multiple linear regression

Multiple linear regression is a straightforward extension of simple linear

regression. The simple linear regression equation:

¼ a þ bX

(16:13 copied from 16:1)

examines the relationship between the value of a variable Y and another

variable X. Often, however, the value of Y might depend upon more than

one variable. For example, the sediment yield of a river may be dependent

on its drainage area plus other factors such as topographic relief, precip-

itation and ﬂow rate.

(a)

–2

–3

(b)

Residual

(c)

(d)

Residual

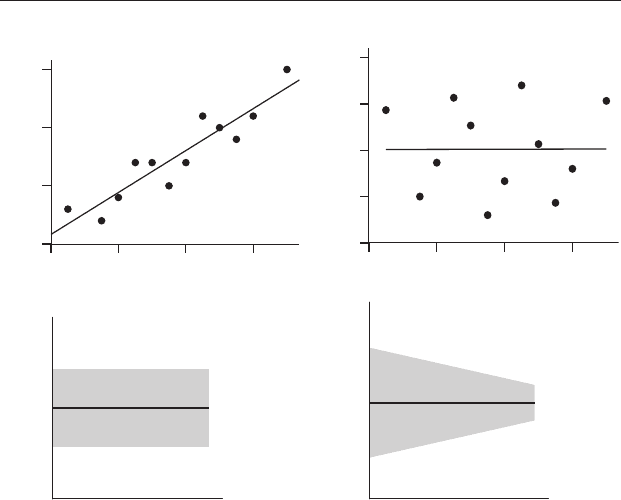
Figure 16.9 (a) Plot of original data in Table 16.4, with ﬁtted regression line

Y = 10.8 + 0.9X. (b) The plot of the residual Y 



against the value of X for

each data point shows a relatively even scatter about the horizontal line.

plot showing one example of heteroscedasticity, where the variance of the

residuals decreases with X.

16.11 Multiple linear regression 223

Therefore, the regression equation could be extended:

¼ a þ b

þ b

(16:14)

which is just Equation (16.13) plus a second independent variable with its

own coeﬃcient of b

and values (X

). You will notice that there is now a

double subscript after the two values of X, in order to specify the ﬁrst variable

(e.g. drainage area) as X

and the second (e.g. topographic relief) as X

Equation (16.14) can be further extended to include additional variables

such as precipitation and ﬂow rate:

¼ a þ b

þ b

::: etc (16:15)

The mathematics of multiple linear regression is complex, but a statistical

package will give the overall signiﬁcance of the regression and, more

importantly, the value for the slope (and its signiﬁcance) for each of the

independent variables.

If the initial analysis shows that an independent variable has no signiﬁ-

cant eﬀect on Y, the variable can be removed from the equation and the

analysis rerun. This process of reﬁning the model can be repeated until only

signiﬁcant independent variables remain, thereby giving the best possible

model for predicting Y. There are several procedures for reﬁning, but the

one most frequently recommended is to initially include all independent

variables, run the analysis and examine the results for the ones that do not

appear to aﬀect the value of Y (i.e. variables with non-signiﬁcant values

of b). The least signiﬁcant is removed and the analysis rerun. This process,

called backward elimination, is repeated until only signiﬁcant variables

remain.

16.12 Further topics in regression

This chapter is an introduction to linear regression analysis. More advanced

analyses include procedures for comparing the slopes and intercepts of two

or more regression lines. Non-linear regression models can be ﬁtted to data

where the relationship between X and Y is exponential, logarithmic or even

more complex. The understanding of simple linear regression developed

here is an essential introduction to these methods, which will be discussed

further in relation to sequence analysis (Chapter 21).

224 Linear regression

16.13 Questions

(1) An easy way to help understand regression is to work through a simple

contrived example. The set of data below will give a regression with

a slope of 0 and an intercept of 10, so the line will have the equation

Y =10+0X:

010

011

110

111

210

211

(a) Use a statistical package to run the regression. What is the value of r

for

this relationship? Is the slope of the regression signiﬁcant? (b) Next, modify

thedatatogiveaninterceptof20,butwithaslopethatisstillzero.(c)

Finally, modify the data to give a negative slope that is signiﬁcant.

(2) The table below gives data for the weight of alluvial gold recovered from

diﬀerent volumes of stream gravel.

Volume of gravel

processed (m

)

Weight of gold

recovered (grams)

1 0.025

2 0.042

3 0.071

4 0.103

5 0.111

6 0.142

7 0.164

8 0.191

9 0.220

16.13 Questions 225

(a) Run a regression analysis, where the volume of gravel is the inde-

pendent variable. What is the value of r

? Is the relationship signiﬁcant?

What is the equation for the relationship between the weight of gold

recovered and the volume of gravel processed? Does the intercept of the

regression line diﬀer signiﬁcantly from zero? Would you expect it to?

Why?

226 Linear regression

17 Non-parametric statistics

17.1 Introduction

Parametric tests are designed for analyzing data from normally distributed

populations. Although these tests are quite robust to departures from

normality, and major ones can often be reduced by transformation, there

are some cases where the population is so grossly non-normal that para-

metric testing is unwise. In these cases a powerful analysis can often still be

done by using a non-parametric test.

Non-parametric tests are not just alternatives to the parametric pro-

cedures for analyzing ratio, interval and ordinal data described in

Chapters 8 to 16. Often geoscientists obtain data that have been measured

on a nominal scale. For example, Table 3.2 gave data for the locations

of 594 tornadoes during the period from 1998–2007 in the southeastern

states of the US. This is a sample containing frequencies in several

discrete and mutually exclusive categories and there are non-parametric

tests for analyzing these types of data (Chapter 18).

17.2 The danger of assuming normality when a population

is grossly non-normal

Parametric tests have been speciﬁcally designed for analyzing data from

populations with distributions shaped like a bell that is symmetrical about

the mean with 66.26% of values occurring within μ ± 1 standard deviation

and 95% within μ ± 1.96 standard deviations (Chapter 7). This distribution

is used to determine the range within which 95% of the values of the sample

mean,

X, will occur when samples of a particular size are taken from a

population. If

X occurs outside the range of μ ± 1.96 SEM, the probability

the sample has come from that population is less than 5%. If the population

227

is not normally distributed the range occupied by 95% of the values of the

mean may be either wider or narrower than assumed, in which case judg-

ments about statistical signiﬁcance made on the basis of the normal dis-

tribution will be misleading.

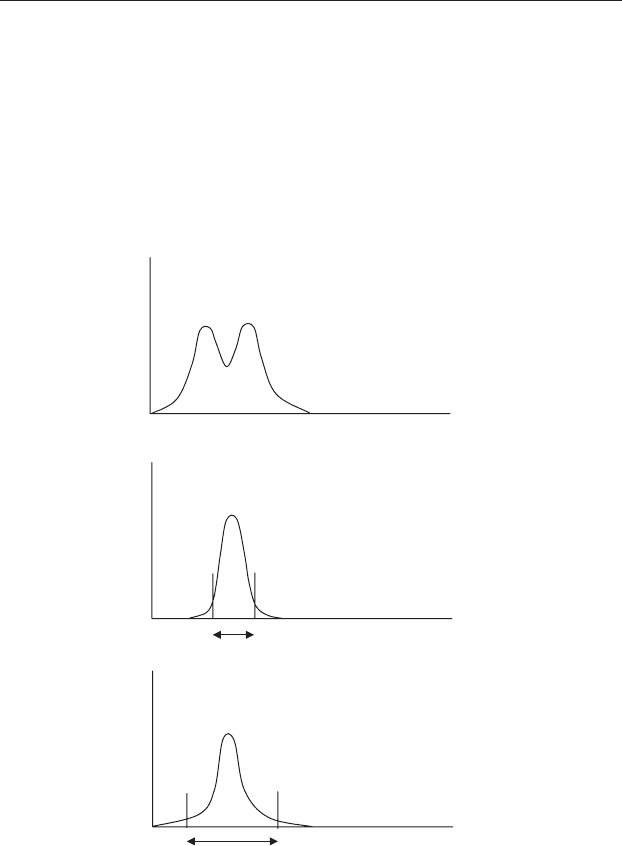
An example is shown in Figure 17.1. The population is bimodal and the

range within which 95% of the values of the means of samples of size n =30

Frequency

(a)

Frequency

(b)

Frequency

(c)

Figure 17.1 Illustration of how the range in which the means of samples

from a grossly non-normal population does not correspond to the expected

range assuming the population is normally distributed. (a) Distribution of a

bimodal population. (b) Actual shape of the distribution of means of sample

size n = 30 from the population shown in (a). (c) Shape of the distribution of

means calculated from the standard error when n = 30 assuming the

population is normally distributed. Horizontal arrows show the range within

which 95% of means would be expected to occur. Note that the expected range

in (c) is much wider than the true range in (b).

228 Non-parametric statistics

from this population actually occur is narrower than the range predicted

if the population is assumed to be normally distributed.

17.3 The value of making a preliminary inspection

of the data

It has already been emphasized that parametric tests for comparing means

can often be applied to data from populations that are not normally

distributed, because the distribution of the means of samples from most

populations will usually be relatively normal (Chapter 6). Once again,

however, the example in Section 17.2 emphasizes the value of graphing

the data to inspect it for normality and homoscedasticity before attempting

a statistical analysis.

The next two chapters describe tests for analyzing nominal scale data,

followed by some non-parametric alternatives to the parametric tests for

independent and related samples described in Chapters 8 to 12, as well as

a non-parametric test for correlation.

17.3 Preliminary inspection of the data 229

18 Non-parametric tests for

nominal scale data

18.1 Introduction

Earth scientists sometimes collect data for which the sampling or exper-

imental units can be assigned to two or more discrete and mutually exclu-

sive categories that are contingent on each other. Consider a paleomagnetic

study of the orientation of Earth’s magnetic ﬁeld using cores collected from

the sea ﬂoor on a traverse perpendicular to the mid-ocean ridge. Roughly

55% of the core samples show the magnetic ﬁeld pointing north and the

remaining 45% show the magnetic ﬁeld pointing south. These directions are

discrete and mutually exclusive categories: a rock may be magnetized to

point to the north or the south, but it cannot ever be both (the case of an in-

between magnetization recorded during a reversal is so rare that it can be

considered negligible). These two possibilities, north vs. south, also make

up the entire set of possible outcomes and are therefore contingent upon

each other: for a sample of 100 cores, a decrease in the number in one

category (e.g. north-polarized rocks) must be accompanied by an increase

in the number in the other (south-polarized rocks) and vice versa.

These are nominal scale data (Chapter 3). The questions researchers ask

about these data are the sort asked about any sample(s) from a population.

First, you may want to know the probability that a sample has been taken

from a population with a known or expected proportion within each of

two or more categories. For example, the ﬁeld of forensics depends heavily

on these types of analyses to build cases based on geological evidence and

there are several documented cases where crimes committed on beaches

have been solved using knowledge of sand mineralogy (Murray and

Tedrow, 1992). Suppose you were hired to examine whether beach sand

found in a murder suspect’s shoes matched that of the beaches on the south

sea island where the victim’s body was found. Scientiﬁc publications

230

describing that locality give the sand mineralogy at all of the beaches on

the island to be 75% coral fragments and 25% basalt grains, and so your null

hypothesis is that the sand from the suspect’s shoes will also have these

proportions. When you examine the sample of 100 grains from the suspect’s

shoes, you ﬁnd that it contains 86 coral fragments and 14 basalt grains.

Before you go and testify in court, you will need to know the probability

that this diﬀerence between the observed frequencies in the sample and

those expected from the composition of the beach is due to chance.

Second, you may want to know the probability that two or more samples

have come from the same population. As an example, consider the handed-

ness of quartz crystals, which is important because of its eﬀect on optical

properties. The handedness arises because there are chains of SiO

tetrahedra

that form a helical spiral around the vertical axis, but the spiral can turn in

either a clockwise or counter-clockwise direction. A manufacturer noticed

that quartz crystals grown using a new type of alloy in the autoclave tended

to be predominantly right-handed. Consequently, 100 quartz crystals grown

with the new alloy method and 100 samples grown using the original one

were compared. For the new method 67 crystals were right-handed and

33 left-handed, while the original method produced 53 right-handed and

47 left-handed. Here too, the diﬀerence between the two samples might be

due to chance, or also be aﬀected by the new procedure.

For both of these examples a method is needed that gives the probability

of obtaining the observed outcome under the null hypothesis. This chapter

describes some tests for analyzing samples of categorical data.

18.2 Comparing observed and expected frequencies:

the chi-square test for goodness of ﬁt

The chi-square test for goodness of ﬁt compares the observed frequencies in

a sample to those expected in a population. The chi-square statistic is the

sum, of each observed frequency minus its expected frequency, squared and

then divided by the expected frequency (and was ﬁrst discussed in Chapter 6):



i¼1

ðo

 e

(18:1)

18.2 Observed and expected frequencies 231

This is sometimes written as:



i¼1

ðf



(18:2)

where f

is the observed frequency and

is the expected frequency.

It does not matter whether the diﬀerence between the observed and

expected frequencies is positive or negative because the square of any

diﬀerence will be positive.

If there is perfect agreement between every observed and expected fre-

quency, the value of chi-square will be zero. Nevertheless, even if the null

hypothesis applies, samples are unlikely to always contain the exact propor-

tions present in the population. By chance, small departures are likely and

larger departures will also occur, all of which will generate positive values of

chi-square. The most extreme 5% of departures from the expected ratio are

considered statistically signiﬁcant and will exceed a critical value of chi-square.

For example, forams can be coiled either counter-clockwise (to the left) or

clockwise (to the right). The proportion of forams that coil to the left is close

to 0.1 (10%), which can be considered the proportion in the population

because it is from a sample of several thousand specimens. A paleontologist,

who knew that the proportion of left- and right-coiled forams shows some

variation among outcrops, chose 20 forams at random from the same

locality and found that four were left-coiled and 16 right-coiled. The ques-

tion is whether the proportions in the sample were signiﬁcantly diﬀerent

from the expected proportions of 0.1 and 0.9 respectively. The diﬀerence

between the population and the sample might be only due to chance, but it

might also reﬂect something about the environment in which the forams

lived, such as the water temperature. Table 18.1 gives a worked example of a

chi-square test for this sample of left- and right-coiled forams.

The value of chi-square in Table 18.1 has one degree of freedom because

the sample size is ﬁxed, so as soon as the frequency of one of the two

categories is set the other is no longer free to vary. The 5% critical value of

chi-square with one degree of freedom is 3.84 (Appendix A), so the pro-

portions of left- and right-coiled forams in the sample are not signiﬁcantly

diﬀerent to the expected proportions of 0.1 to 0.9. The chi-square test for

goodness of ﬁt can be extended to any number of categories and the degrees

of freedom will be k − 1 (where k is the number of categories). Statistical

packages will calculate the value of chi-square and its probability.

232 Non-parametric tests for nominal scale data