Степанов А.Г. Динамика машин
Подождите немного. Документ загружается.

Далее, продифференцировав (6.35) по t , получим
( )
∂
∂
π
π
π π
U x t
t l
j x
a
l
j C a
l
j t D a
l
j t
j j
j
,
sin sin cos= ⋅ − +
=
∞
∑
1
. (6.42)
При t = 0, это выражение будет
( )
∂
∂
ϕ
π
U x
t
x D
a
l
j x
j
j
,
( )
0
1
= =
=
∞
∑
. (6.43)
Если функции f (x) и
ϕ
(x) таковы, что в интервале (0, l) их можно разложить в ряд
Фурье [59], то условия (6.42) и (6.43) будут выполняться, если положить
C
l
f x
l
j x d x
j
l
=
∫
2
0
( )sin
π
, (6.44)
D
a
l
j
l
x
l
j x d x
j
l
π
ϕ
π
=
∫
2
0
( )sin ,
или
D
a j
x
l
j x d x
j
l
=
∫
2
0
π
ϕ
π
( )sin
. (6.45)
Пример 6.3. Исследовать свободные колебания струны шахтной подъемной
установки, рассмотренной в примере 6.1.
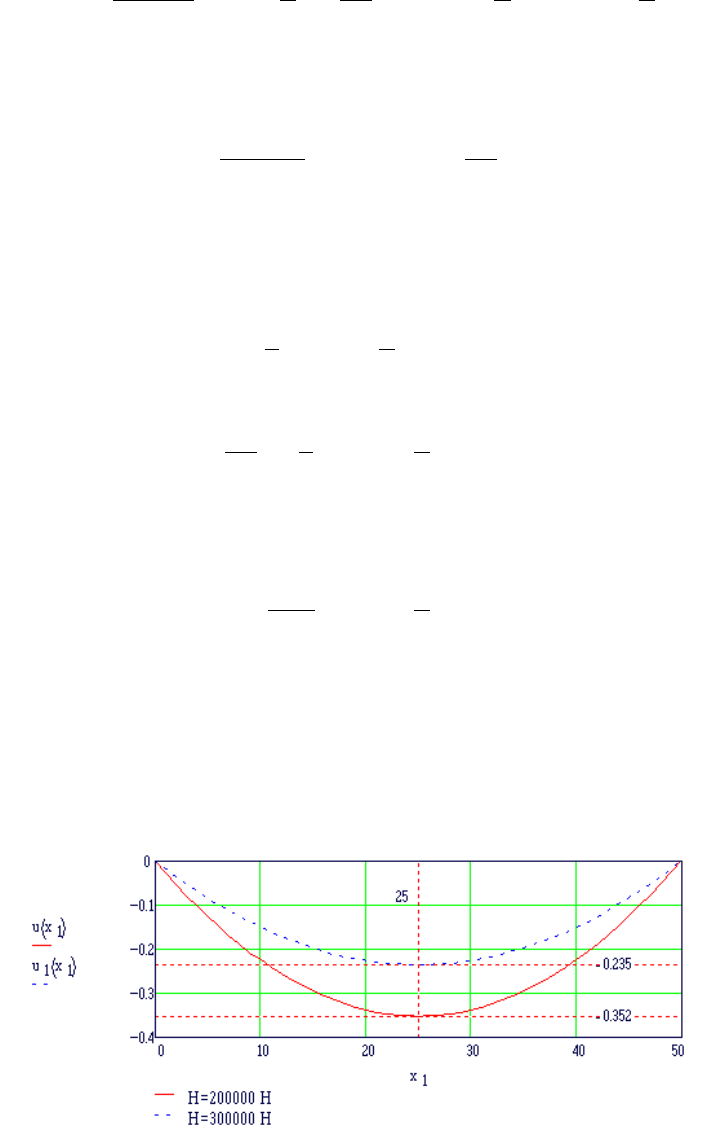
Траектория струны каната при натяжении Н = 200000 Н показана на рис. 6.10.
Перенесем кривую U(x
1
) на рис. 6.17 и по уравнению (6.18) построим траекторию U
1
(x
1
) для
натяжения Н
1
= 300000 Н.
Рис. 6.17.Траектории каната при различных натяжениях
Если из координат первой траектории вычесть координаты второй, то получим
траекторию струны относительно ее первоначального положения при увеличении
натяжения от Н до Н
1
. Характеристика
( ) ( ) ( )
f x U x U x
1 1 1 1
= −
показана на рис. 6.18.
202
202

Рис. 6.18. Характеристика
( ) ( ) ( )
f x U x U x
1 1 1 1
= −
Следовательно, если дополнительную силу
∆H H H= −
1 2
убрать, то струна будет совершать
свободные поперечные колебания относительно первоначально траектории при натяжении
H.
Таким образом, для рассматриваемого примера, в котором концы струны
закреплены, можно записать краевые условия задачи.
Граничные условия
( )
( )
U t
U l t
0 0
0
, ,
, .
=
=
Начальные условия
U x f x U x U x
U
t
x
t
( , ) ( ) ( ) ( ),
( ) .
0
0
1 1 2 1
0
= = −
= =
=
∂
∂
ϕ
Таким образом, для заданных граничных условий, в соответствии с (6.36)
собственные числа будут
( )
k
l
j j
j
= =
π
1 2, ...
.
Коэффициенты разложения в ряд Фурье определяются по зависимостям (6.44), (6.45).
Так как
( )
ϕ x = 0
то коэффициенты
D
j
= 0,
а
( )
C
l
f x
l
jx dx
j
l
=
∫
2
1 1
0
1
sin .
π
Для оценки свободных колебаний построим характеристики
( )
U x t
j
,
, используя
уравнение (6.39).
( )
U x t k xC ak t
j j j j
, sin cos ,=
Здесь
a
T
p
H
p
= =
cosα
- скорость распространения поперечных волн в продольном
направлении при натяжении каната T.
Если рассматривать поперечные колебания струны в середине пролета
x
l
=
2
, то
U
l
t jC t
j j j
2 2
, sin cos ,
=
π
ω
203
203

здесь
ω π
j
a
l
j=
- частота собственных колебаний, с
-1
.
Из формулы видно, что для всех четных гармоник (тонов)
U
l
t
j
j
2
0
2 4
,
, ...
=
=
, т. к.
sin
, ...
π
2
0
2 4
j
j=
=
.
Для нечетных гармоник
sin
, ...
π
2
1
1 3
j
j=
=
, поэтому
U
l
t C t
j j j j
2
1 3
, cos
, ...
=
=
ω
.
Очевидно, коэффициенты разложения в ряд Фурье
C
j
являются амплитудой
колебаний. Вычислим значения собственных чисел
k
j
, частот
ω
j
и коэффициентов
C
j
для
первых пяти нечетных гармоник. Результаты вычислений приведены в табл. 6.1.
Таблица 6.1
Собственные числа
k
j
, частоты
ω
j
и коэффициенты
C
j
j 1 3 5 7 9
k
j
0,063 0,188 0,314 0,44 0,565
ω
j
, c
-1
8,35 25,06 41,77 58,48 75,18
C
j
, м
-0,117 -0,0043 -0,00074 -0,00018 -0,000036
C
j
, м
-0,-86 -0,003 -0,00068 -0,00025 -0,00018
Интересно посмотреть, как изменится максимальная разность ординат и значения
коэффициента C
nj
при замене формул цепных линий параболами. Для этого по уравнению
(6.24) вычислим траектории для натяжений H и H
1
и определим функцию
( ) ( ) ( )
f x U x U x
n n n1 1 1 1
= −
.
Здесь индекс n говорит о том, что уравнения принадлежат к параболическому закону
изменения траекторий. Максимальная разность ординат равна 0,083 м. Значения
коэффициентов C
nj
приведены в последней строке табл. 6.1.
Предварительно можно заключить, что амплитуда колебаний приближенной
траектории (парабола) будет меньше в 0,117/0,083 = 1,41 раза.
Графики колебаний первой, третьей и пятой гармоник показаны на рис. 6.19.
Амплитуда третьей гармоники в 0,117/0,0043 = 27 раз меньше первой и показана на рис.
6.19 пунктирной линией.
204
204
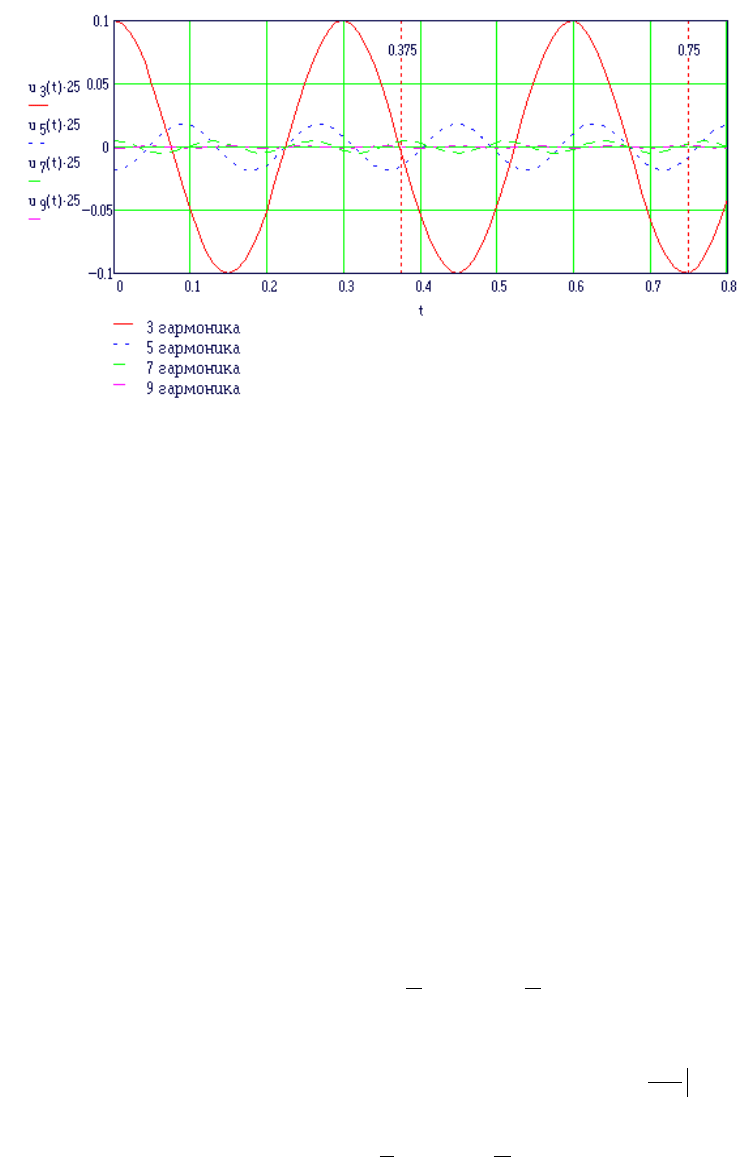
Рис. 6.19. Графики колебаний первой, третьей и пятой гармоник
Пятая гармоника, при принятом масштабе, практически сливается с нулевой линией.
Соотношение 3, 5, 7 и 9 гармоник показаны на рис. 6.20. Масштаб оси ординат увеличен в
25 раз.
Рис. 6.20. Колебания третьей, пятой, седьмой и девятой гармоник
Из приведенных графиков видно, что для данной задачи переходный процесс
определяется, в основном, первой гармоникой. При принятом масштабе графики первой
гармоники и суммы всех гармоник практически не отличаются. Такое заключение приводит
к мысли, что для исследования поперечных колебаний струны шахтного подъемника,
имеющей большое натяжение и малую длину, допустим укрупненный анализ
колебательных процессов.
6.3.2. УКРУПНЕННЫЙ АНАЛИЗ КОЛЕБАТЕЛЬНОГО ПРОЦЕССА СТРУНЫ
Уравнение (6.40) характеризует колебательный процесс струны. Перепишем это
уравнение для первой гармоники, опуская индекс j.
( )
U x t k x C a
l
t D a
l
t, sin cos sin .= +
π π
В примере 6.3 было показано, что для начальных условий
( ) ( )
,0, xfxU =
( )
0
0
=ϕ=
∂
∂
=
x
t
U
t
постоянные интегрирования равны
( )
D C
l
f x
l
xdx
l
= =
∫
0
2
0
; sin
π
.
205
205
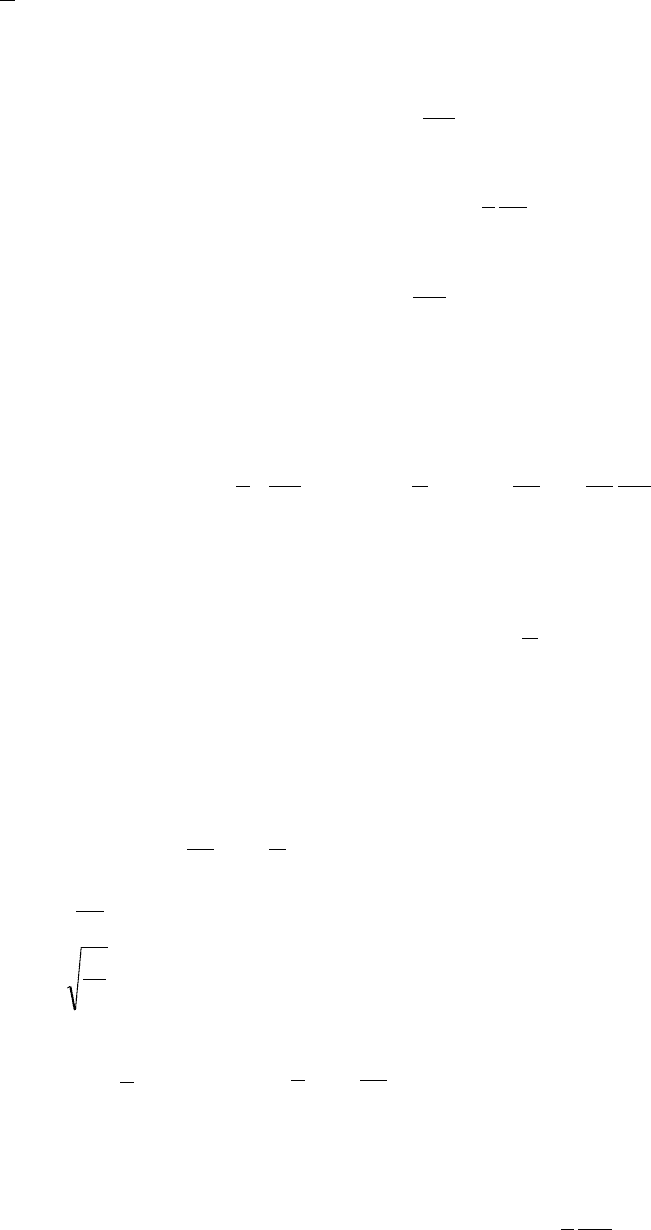
Если струну вывести из первоначального положения, придав пролету в сечении
x
l
=
2
величину f, то при принятых выше допущениях, траектория струны характеризуется
уравнением (6.25)
( )
( )
U x
f
l
x l x,0
4
2
= − −
.
Если в эту формулу подставить значение
f
gp
H
l= −
1
8
2
, то получим уравнение (6.24)
( )
( )
U x
g p
H
x x l,0 = −
,
которое тождественно уравнению (6.25). Подставив значения
( ) ( )
f x U x= ,0
, получим
выражение для коэффициента C
( )
C
l
f
l
x l x
l
x dx f
g p
H
l
l
= − − = − =
∫
2 4 32 4
2
0
3 3
2
sin .
π
π π
Тогда
( )
U x t C k x a
l
t, sin cos .=
π
Это уравнение можно представить
( )
( )
U x t A x t, cos ,= ω
(6.46)
где
( )
A x C kx f
l
x= = −sin sin
32
3
π
π
- амплитуда колебаний струны в сечении x;
ω
π
=
a
l
- частота колебаний, с
-1
.
Здесь
a
H
p
=
- скорость распространения поперечных волн в продольном направлении,
м⋅с
-1
.
Для
x
l
=
2
амплитуда
A
l
f f
2
32
1 032
3
= − =
π
,
. Таким образом, можно считать, что
амплитуда колебаний равна стреле провеса f. С физической точки зрения это понятно,
т. к. если к струне приложить возмущающее воздействие, которое вызывает изменение
траектории со стрелой провеса f, а затем возмущающее воздействие убрать, то должны
последовать свободные колебания с амплитудой
A f
g p
H
l= = −
1
8
2
.
Уравнение (6.46) можно записать
( )
U t f t= cos .ω
(6.47)
206
206
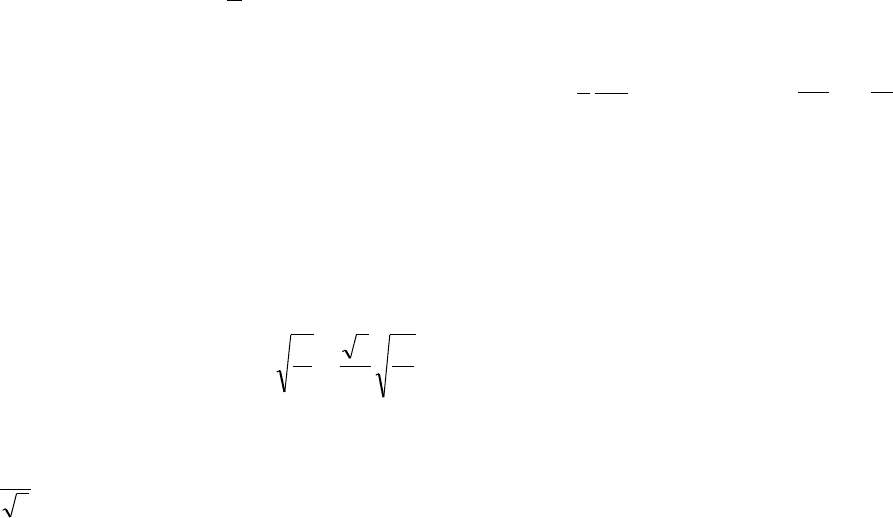
Известно, что уравнение (6.47) есть общее решение уравнения
′′
+ =U Uω
2
0
при начальных
условиях
t U f U= =
′
=0 0; ;
. В свою очередь последнее дифференциальное уравнение
характеризует свободные колебания массы, соединенной упругим элементом жесткостью
C m= ω
2
. Таким образом, для упрощенной оценки поперечных колебаний струны,
последнюю можно представить невесомой нитью, масса которой
m pl=
сосредоточена в
середине пролета
x
l
=
2
. Под действием силы от веса gm, струна имеет стрелу провеса f, т.
е. gm = cf. Здесь c - эквивалентная жесткость струны при перемещении ее в поперечном
направлении, Н⋅м
-1
. Подставив абсолютное значение
f
g p
H
l=
1
8
2
, получим
c
gm
f
H
l
= = 8 .
Таким образом, дифференциальное уравнение, характеризующее свободные
колебания массы m, которая соединена с упругим элементом, имеющим жесткость c будет
mU cU
′′
− = 0,
или
′′
− =U Uω
2
0,
ω = =
c
m l
H
p
8
Видно, что при укрупненной оценки частоты поперечных колебаний получится в
π
8
111= ,
раз меньше по сравнению с точным методом решения задачи. Амплитуда
колебаний первой гармоники при точном методе равна 1,032 f, а при укрупненной оценке
- равна f.
Полученные данные позволяют сделать вывод о возможности укрупненной оценки
динамических процессов гибких однородных тяжелых нитей (струны канатов, ленты
конвейеров, провода линий электропередач и т. д.), при этом погрешность не будет
превышать 11 %.
При таком допущении процессы вынужденных колебаний характеризуются
уравнениями, рассмотренными в разделах 3, 4, а полученные результаты могут быть
распространены и на вынужденные колебания гибких однородных тяжелых нитей.
7. ДИНАМИЧЕСКИЕ ПРОЦЕССЫ МНОГОМАССОВЫХ МЕХАНИЧЕСКИХ
СИСТЕМ
В разделе 1.1 было показано, что для изучения динамических процессов в машине,
последнюю необходимо представить эквивалентной схемой, в которой n сосредоточенных
масс соединены вязкоупругими элементами (рис. 1.2, 1.3, 1.4). Любая эквивалентная схема,
в которой количество масс более двух, характеризуется системой дифференциальных
уравнений, которые могут быть решены численными методами.
Для математического описания механической системы, состоящей из n
сосредоточенных масс, соединенных вязкоупругими элементами, применяется принцип
Даламбера, который применительно к произвольной системе был предложен Ж. Лагранжем
в 1760 г. [75].
Метод Лагранжа основан на понятии обобщенных координат и сил. Под
обобщенными координатами n(t) понимается независимые друг от друга однозначные
функции времени, при помощи которых описываются кинематические параметры
207
207

механической системы. Первые производные от обобщенных координат по времени
′
n t( )
называются обобщенными скоростями.
В качестве обобщенных координат могут быть использованы любые независимые
параметры: координаты положения масс, углы поворота и т. д.
Для получения математической модели, характеризующей динамику механической
системы, в основу положено уравнение Лагранжа [76]
d
dt
T
n
T
n
П
n
Ф
n
P
n
∂
∂
∂
∂
∂
∂
∂
∂
′
− = − −
′
+ ,
где n - обобщенная координата, м;
t - текущее время, с;
T, П - кинетическая и потенциальная энергии системы, Н⋅м;
Ф - диссипативная функция, характеризующая силы вязкого сопротивления, Н⋅м⋅с
-1
;
P
n
- обобщенная сила, Н.
Уравнение Лагранжа используют для изучения динамических процессов любой
механической системы, независимо от того, сколько масс входит в систему, как движутся
эти массы и какое движение рассматривается (абсолютное или относительное). Системы
дифференциальных уравнений имеют общие закономерности, которые позволяют в
дальнейшем, при наличии эквивалентной схемы машины, записывать математическую
модель без вывода, который приведен применительно к трехмассовой механической
системы.
7.1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТРЕХМАССОВОЙ МЕХАНИЧЕСКОЙ
СИСТЕМЫ
В качестве эквивалентной схемы механической системы, в которой три массы
соединены двумя вязкоупругими элементами, примем схему, показанную на рис. 1.4. Такой
эквивалентной схеме могут соответствовать многие машины, в том числе, лифтовые и
грузовые подъемники. На этой схеме, в качестве обобщенных координат приняты x, y и z,
относительно которых перемещаются массы машины m
м
, груженого сосуда m
сy
, и
порожнего сосуда m
cx
. Машина и сосуды соединены канатами с коэффициентами жесткости
с
y
, и с
z
, и вязкости µ
y
и µ
z
. Обобщенными силами являются силы двигателя F
дв
(x
′
) , тормоза
F
т
(t)
и вредных сопротивлений P
y
и P
z
. Обратим внимание, если обобщенная сила
направлена в направлении обобщенной координаты и способствует ее возрастанию, то она
имеет знак плюс. В противном случае, ее следует принимать со знаком минус. Полное
изменение потенциальной энергии системы можно представить в виде
П П П П П П П
y z ky kz y z
= − + − + +
∂ ∂
,
(7.1)
здесь П
y
, П
z
- изменение потенциальной энергии масс m
cy
и m
cz
при перемещении их
соответственно на величину y и z , Н⋅м;
П
ky
, П
kz
- изменение потенциальной энергии массы упругих элементов (канатов),
Н⋅м;
П
∂
y
, П
∂
z
- изменение потенциальной энергии деформированных канатов, Н⋅м.
Если груженый сосуд имеет массу m
сy
, а порожний - m
cz
, то
П gm y П gm z
y cy z cz
= =; ,
где g - ускорение свободного падения, м⋅с
-2
.
208
208

Для определения изменения потенциальной энергии массы канатов вернемся к
схеме, показанной на рис. 1.6.
Если за единицу времени перемещение верхнего конца каната произошло на
величину x, а нижнего y, то, в соответствие с зависимостью (1.2), элементарный участок dδ
будет иметь перемещение
∆ = −
−
x
x y
l
y
δ.
Тогда элементарное изменение массы каната
dП qpd qp x
x y
l
d
ky
y
= = −
−
δ∆ δ δ.
Следовательно
П qp x
x y
l
d qpl
x y
gm
x y
ky
y
y ky
l
y
= −
−
=
+
=
+
∫
δ δ
2 2
0
.
Аналогично рассуждая, можно записать изменение потенциальной энергии массы
порожней ветви
П gm
x z
kz kz
=
+
2
,
здесь p - линейная плотность каната, кг;
m
ky
и m
kz
- массы канатов груженой и порожней ветвей, кг.
Если упругий элемент имеет жесткость c и полную деформацию λ
n
, то
потенциальная энергия этой связи определится [55]
П
c
n∂
λ=
2
2
.
Для рассматриваемого случая с увеличением y по сравнению с x полная деформация
груженой ветви λ
ny
уменьшается, а при увеличении z по сравнению с x полная деформация
порожней ветви λ
nz
увеличивается, поэтому
λ λ λ λ
ny y nz z
x y z x= + − = + −; .
Тогда изменение потенциальной энергии деформированных канатов груженой и
порожней ветвей
( )
( )
П
с
x y П
с
z x
y
y
y z
z
z∂ ∂
λ λ= + − = + −
2 2
2
2
; .
Статическая деформация ветвей канатов λ
y
и λ
z
в соответствие с (3.2), имеет вид
209
209

λ λ
y
y
cy
ky
z
z
cz
kz
q
с
m
m
q
с
m
m
= +
= +
2 2
; .
Подставив найденные значения в уравнения (7.1), получим полное изменение
потенциальной энергии системы
( )
( )
.
2222
22
xz
c
yx
c
zx
m
yx
mzmymgп
z
z
y
y
kzkyczcy
−+λ+−+λ+
+
−
+
+−=
(7.2)
Кинетическая энергия системы
T T T T T T
x y z ky kz
= + + + + ,
(7.3)
где T
x
, T
y
, T
z
, T
ky
, T
kz
, - кинетическая энергия, соответственно, органов навивки с
приводом, груженого и порожнего сосудов, канатов, поднимающейся и опускающейся
ветвей, Н⋅м.
(
)
(
)
(
)
T
m
x T
m
y T
m
z
x
м
y
cy
z
cz
=
′
=
′
=
′
2 2 2
2 2 2
; ; .
Кинетические энергии канатов определяются по уравнению (1.5)
( )
( )
( ) ( )
T
p
g
x
x y
l
d
m
x x y y
T
m
x x z z
ky
y
ky
l
kz
kz
y
=
′
−
′
−
′
=
′
+
′ ′
+
′
=
′
+
′ ′
+
′
∫
2 2 3
2 3
2
2
2
0
2 2
δ δ ,
.
Подставив полученные значения в уравнение (7.3) найдем кинетическую энергию системы
( )
( )
( )
( )
( )
[ ]
( ) ( )
[ ]
T
m
x
m
y
m
z
m
x x y y
m
x x z z
м
cy
cz
ky
kz
=
′
+
′
+
′
+
′
+
′ ′
+
′
+
′
+
′ ′
+
′
2 2 2 2 3 2 3
7 4
2
2
2
2
2
2 2
. ( . )
Диссипативная функция, или функция рассеивания - понятие которое было введено
Рэлеем, представим в виде положительной квадратичной функции [74]
( ) ( )
[ ]
Ф y x z x
y z
=
′
−
′
+
′
−
′
1
2
2 2
µ µ ,
(7.5)
где µ
y
, µ
z
- коэффициенты диссипации, характеризующие силы вязкого трения груженой
и порожней ветвей канатов.
Используя выражение (7.2) и (7.4), определим частные производные по координатам
x, y, z.
210
210
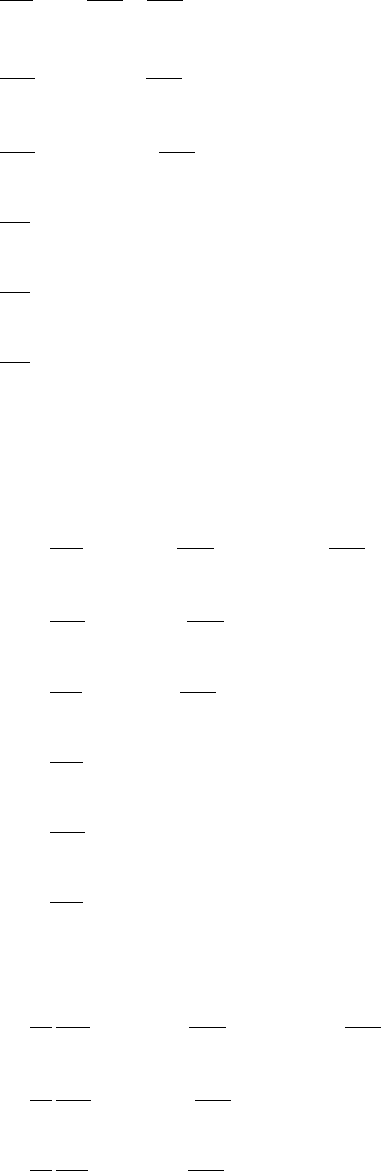
( )
( )
( )
( )
.0
;0
;0
;
2
;
2
;
22
=
∂
∂
=
∂
∂
=
∂
∂
−+λ+
+−=
∂
∂
−+λ−
+=
∂
∂
−+λ−−+λ+
−=
∂
∂
z
T
y
T
x
T
xzс
m
mg
z
П
yxс
m
mg
y
П
xzсyxс
m
m
g
x
П
zz
kz
cz
yy
ky
cy
zzyy
kz
ky
Из уравнений (7.4), (7.5) определяются частные производные по обобщенным
скоростям
′ ′ ′
x y z, ,
( ) ( )
( )
( )
( ) ( )
[ ]
( )
( )
.
;
;
;2
6
;2
6
;2
6
2
6
xz
z
Ф
xy
y
Ф
xzxy
x
Ф
zx
m
zm
z
T
yx
m
ym
y
T
zx
m
yx
m
xm
x
T
z
y
zy
kz
сz
ky
cy
kz
ky
“
′
−
′
µ=
′
∂
∂
′
−
′
µ=
′
∂
∂
′
−
′
µ+
′
−
′
µ−=
′
∂
∂
′
+
′
+
′
=
′
∂
∂
′
+
′
+
′
=
′
∂
∂
′
+
′
+
′
+
′
+
′
=
′
∂
∂
Тогда первые члены уравнения Лагранжа запишем как
( ) ( )
( )
( )
.2
6
;2
6
;2
6
2
6
zx
m
zm
z
T
dt
d
yx
m
ym
y
T
dt
d
zx
m
yx
m
xm
x
T
dt
d
kz
сz
ky
сy
kz
ky
м
′′
+
′′
+
′′
=
′
∂
∂
′′
+
′′
+
′′
=
′
∂
∂
′′
+
′′
+
′′
+
′′
+
′′
=
′
∂
∂
Подставив эти выражения в уравнение Лагранжа и сделав преобразования, получим
дифференциальные уравнения, характеризующие динамический процесс трехмассовой
механической системы
211
211
