Степанов А.Г. Динамика машин
Подождите немного. Документ загружается.


Если сравнить этот рисунок с рис. 5.4 и 5.5, то видно, что замедление органа навивки
xx с стало иметь меньшую амплитуду колебаний, однако замедление концевого груза yy т
колеблется с большей амплитудой.
Таким образом, в системе автоматического регулирования замедления, построенной
по такому принципу, не представляется возможным уменьшить колебания концевого груза.
Отметим еще раз, что чрезмерные колебания массы m
y
могут вызвать проскальзывание
канатов на многоканатном подъеме, или набегание сосуда на канат на наклонном подъеме.
Построенная таким образом система автоматического регулирования замедления,
предназначенная для устранения опасных режимов на подъемной установке, может стать
причиной появления этих недопустимых явлений. В реальной машине, тормозное
устройство которой обладает запаздыванием и гистерезисом, могут сформироваться
динамические процессы, которые усилят колебания машины и концевого груза.
Этими причинами объясняются неудачные попытки использования СРПТ на
многоканатном подъеме. Использование таких СРПТ на наклонных установках, у которых
колебания массы m
x
незначительны, позволяет получать замедление машины близкое к
заданному и тем самым исключать набегание сосуда на канат при предохранительном
торможении. Следует отметить, что автором со своими учениками разработан ряд более
простых разомкнутых систем торможения, которые были внедрены на шахтах Инты,
Воркуты, Урала и Кузбасса [4, 5, 7].
5.6. СИСТЕМЫ АВТОМАТИЧЕСКОГО ДЕМПФИРОВАНИЯ КОЛЕБАНИЙ
Рассмотрим теоретическую возможность демпфирования колебаний за счет
применения системы автоматического регулирования. Эта система регулирования должна
сформировать двигательное или тормозное усилие по определенному закону.
Если машину представить двухмассовой механической системой, то переходный
процесс характеризуется системой уравнений (4.1), которые приводятся к уравнению (4.3)
′′
+
′
+ =∆ ∆ ∆2
2 2
2
2
µ ω a t( ).
Для реальных машин корни характеристического уравнения
r
1 2 2 2
2
2
2
,
,= − ± −µ µ ω
всегда комплексные (т. к.
2
ω
>>
2
µ
) и, как следствие, переходные процессы носят
колебательный характер.
Для того чтобы переходный процесс был устойчивым и апериодическим,
необходимо чтобы корни
1
r
и
2
r
были действительными и отрицательными. Это условие
может быть выполнено при
2
µ
>
2
ω
, т. е.
1
2
µ
y
x y
x y
y
x y
x y
m m
m m
c
m m
m m
+
>
+
.
(5.13)
Коэффициент, характеризующий силы вязкого сопротивления, К
у
можно выразить через
логарифмический декремент колебаний л
2
из формулы (4.46)
172
172

µ
δ
π
y
y
y
x y
x y
m
c
m m
m m
=
+
2
.
Экспериментальные исследования показали, что для шахтных подъемных установок
2
δ
≈
0,15 , [72].
Если неравенство (5.13) заменить равенством, то можно определить условное значение
логарифмического декремента колебаний
y
δ
, при котором процесс будет апериодическим
δ π
y
y
x y
m
m m
=
+
2
.
При
yx
mm =
, δ
y
= 1,41π, т. е. в 25 раз больше реального
2
δ
.
Этот коэффициент назван условным логарифмическим декрементом колебаний, так
как в реальной машине отсутствуют силы вязкого сопротивления, способные
задемпфировать колебательный процесс.
Однако если допустить, что такие силы вязкого демпфирования можно ввести в
механическую систему, то переходный процесс станет апериодическим. Создание сил,
пропорциональных силам вязкого демпфирования можно возложить на систему
автоматического регулирования.
Действительно, на основании первого уравнения системы (4.1) можно записать
m x c x y F F t x y
x y ст y
′′
+ − = − +∑ −
′
−
′
( ) ( ) ( ).µ
(5.14)
Рассмотрим случай торможения машины при отключенном электродвигателе. Для этого
случая
∑ = −F t F t
т
( ) ( ),
где
F t
т
( )
- тормозное усилие, приложенное к массе m
x
, Н.
μ
y
- коэффициент диссипации, соответствующий условному логарифмическому
декременту колебаний, Нсм
-1
.
Закон изменения тормозного усилия можно принять экспоненциальным, который
характеризуется уравнением (1.28)
F t F e
т
t
( ) ( )
max
= −
−
1
τ
.
Таким образом, для того чтобы получить переходный процесс без колебаний, на
тормозную систему необходимо возложить обязанности создания суммарного
регулируемого тормозного усилия
F t F t F t F e k x y
p m к
t
y
( ) ( ) ( ) ( ) ( )
max
= + = − +
′
−
′
−
1
τ
. (5.15)
Здесь
F t k x y
к y
( ) ( )=
′
−
′
- корректирующая составляющая тормозного усилия, Н;
k
y
- коэффициент усиления системы автоматического регулирования, Н- сс м
-1
.
Возникает вопрос, можно ли в реальных тормозных устройствах реализовать получение
корректирующей составляющей F
к
(t) и суммарного регулируемого тормозного усилия F
р
(t)?
173
173
Эта задача решена путем математического моделирования процесса торможения с
наложенными ограничениями.
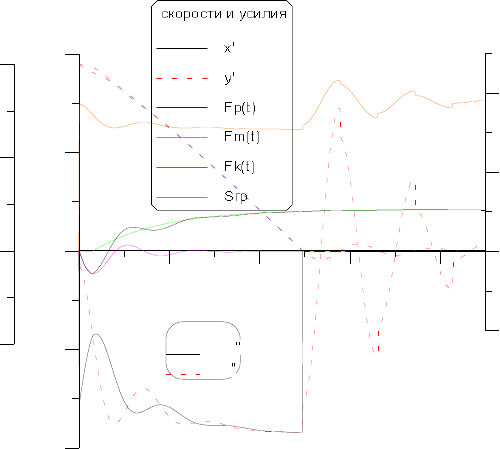
На рис. 5.9, показан процесс торможения машины при подъеме груза. Компьютерная
программа позволяет получить ответ на вопрос, как должно изменяться тормозное усилие,
чтобы обеспечить апериодический переходный процесс.
При подаче сигнала на торможение к машине прикладывается ступенью возмущение,
равное статическому сопротивлению F
cт
, которое вызывает колебательный процесс. В
первоначальный момент замедление массы m
y
(y”) обусловлено силой вредного
сопротивления - R
y
, а замедление массы m
x
(x”) - приложением статического сопротивления
- F
ст
. На фоне экспоненциальной характеристики F
m
(t) показаны корректирующая F
к
(t) и
результирующая F
p
(t) составляющие тормозного усилия. Видно, что через секунду, после
начала торможения, замедления y” и x” практически равны и процесс до остановки
машины совершается без колебаний. На рисунке показаны закономерности изменения
скоростей x′ и y′ , а также полное натяжение каната S
гр
.
0 . 0 0 2 . 0 0 4 . 0 0 6 . 0 0 8 . 0 0
в р е м я , с
- 2 . 0 0
- 1 . 0 0
0 . 0 0
1 . 0 0
2 . 0 0
у с к о р е р и е , м / с
- 4 . 0 0
0 . 0 0
4 . 0 0
8 . 0 0
с к о р о с т ь , м / с
- 1 0 0 . 0 0
0 . 0 0
1 0 0 . 0 0
2 0 0 . 0 0
у с и л и е , к Н
у с к о р е н и е
x
y
2
Рис. 5.9. Торможение машины при подъеме груза с регулируемой характеристикой тормоза
Обратим внимание на тот факт, что для получения апериодического процесса, в
период холостого хода тормоза к машине должно быть приложено движущее усилие.
Характер нарастания результирующего усилия F
p
(t) не существенно отличается от
экспоненциального и вселяет уверенность в возможности реализации синтезированной
тормозной характеристики на реальной машине. После остановки органа навивки (x′ = 0),
масса m
y
совершает свободные колебания и в канате возникают максимальные нагрузки.
Так как в реальных машинах при торможении получение движущего усилия в период
холостого хода тормоза затруднительно, то для доказательства возможности
демпфирования колебательного процесса, при математическом моделировании примем
условие, что при F
p
(t) < 0, результирующее тормозное усилие равно нулю. Характеристики
процесса торможения при подъеме груза, соответствующие этому условию, показаны на
рис. 5.10.
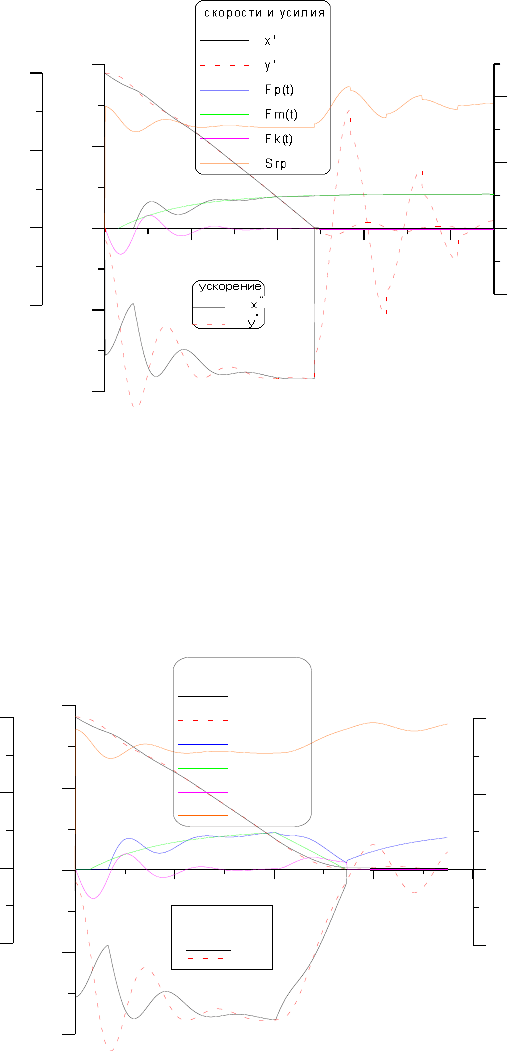
Видно, что по сравнению с рис. 5.9, для демпфирования колебаний после холостого
хода, на тормоз возлагаются более сложные задачи. Регулирующее усилие F
p
(t) должно
резко возрасти, а затем изменяться по закону, показанному на рис. 5.10. При этом время
холостого хода увеличивается. В результате, в процессе торможения колебания замедлений
x” и y” существенно снижены. После остановки машины, также как для процесса,
показанного на рис. 5.1, наблюдаются большие колебания массы m
y
.
174
174
Обратим внимание на некоторые искажения характеристик свободных колебаний
массы m
y
по сравнению с гармоническими колебаниями. Характерные изломы кривых S
гр
и
y” объясняется тем, что во втором уравнении системы (4.1) изменяется знак перед силой
трения R
y
при изменении знака скорости y′. В математической модели это свойство
реализовано функцией Кронеккера R
y
sign y′.
Рассмотренный пример показывает возможность демпфирования колебаний только в
процессе замедления машины и оставляет нерешенной задачу снижения динамических
нагрузок, возникающих после остановки машины.
0 . 0 0 2 . 0 0 4 . 0 0 6 . 0 0 8 . 0 0
в р е м я , с
- 2 . 0 0
- 1 . 0 0
0 . 0 0
1 . 0 0
2 . 0 0
у с к о р е н и е , м / с
- 4 . 0 0
0 . 0 0
4 . 0 0
8 . 0 0
с к о р о с т ь , м / с
- 1 0 0 . 0 0
0 . 0 0
1 0 0 . 0 0
2 0 0 . 0 0
у с и л и е , к Н
2
Рис. 5.10. Торможение машины при подъеме груза с учетом холостого хода тормоза
Для того чтобы уменьшить динамические нагрузки после остановки машины
целесообразно перед остановкой машины, с интенсивностью пропорциональной периоду
колебаний, уменьшить величину тормозного усилия, а после того, как масса m
x
остановится - тормозное усилие увеличить до величины, обеспечивающей надежное
стопорение машины [6].
y "
0 . 0 0 2 . 0 0 4 . 0 0 6 . 0 0 8 . 0 0
- 2 . 0 0
- 1 . 0 0
0 . 0 0
1 . 0 0
2 . 0 0
у с к о р е н и е , м / с
- 4 . 0 0
0 . 0 0
4 . 0 0
8 . 0 0
с к о р о с т ь , м / с
- 1 0 0 . 0 0
0 . 0 0
1 0 0 . 0 0
2 0 0 . 0 0
у с и л и е , к Н
с к о р о с т и и у с и л и я
x '
y '
F p ( t )
F m ( t )
F k ( t )
S г р
у с к о р е н и я
x "
2
Рис. 5.11. Торможение машины с синтезированной тормозной характеристикой
Характеристика динамического процесса показана на рис. 5.11. Видно, что в
первоначальный момент массы m
x
и m
y
начинают разгоняться, совершая большие
175
175

колебания. Синтезированное тормозное усилие F
p
(t) демпфирует колебания и процесс
приближается к апериодическому. Перед остановкой машины, за время равное периоду
колебаний, тормозное усилие уменьшается. После остановки массы
m
x
(x′ = 0), к неподвижной машине прикладывается полное тормозное усилие. В результате,
амплитуда свободных колебаний массы m
y
значительно меньше, по сравнению с
процессами, показанными на рис. 5.9 и 5.10.
Таким образом, исследования показывают возможность синтеза тормозного усилия,
способного задемпфировать колебания в элементах машины. Эти закономерности можно
распространить и на процессы разгона. Для достижения поставленной задачи системы
автоматического регулирования электроприводом или тормозом должны иметь обратную
связь, сигнал которой пропорционален разности скоростей
( )
′
−
′
x y
с коэффициентом
усиления k
y
> μ
y
.
Для практической реализации предложенного способа демпфирования колебаний
необходимо измерить скорость машины и сосуда. Если для измерения скорости машины нет
затруднений, то измерение скорости подъемного сосуда и трансляции этого сигнала в
здание, где расположена подъемная машина и система регулирования, представляет
определенные трудности.
В принципе, скорость сосуда можно измерить косвенным путем. Например, замерив
усилие в канате, можно выделить динамическую составляющую и при известной массе
концевого груза определить замедление (ускорение) сосуда, проинтегрировав которое,
можно получить скорость сосуда, Такой способ получения информации о поведении
концевого груза также нельзя считать надежным и приемлемым. Основная сложность при
этом заключается в постоянном контроле за натяжением канатов. Известные датчики и
аппараты контроля громоздки и могут использоваться только при экспериментальных
исследованиях. О повседневном применении такой аппаратуры не может быть и речи.
Для практической реализации системы предохранительного торможения, способной
демпфировать колебания сосуда в канате, может быть использована схема, в которой
регулируемая величина тормозного усилия формируется суммой нерегулируемого
тормозного усилия F
m
и тормозного усилия, пропорционального сумме сигналов
производной замедления органа навивки и производной тормозного усилия. Докажем это
положение.
Уравнение (5.14) без учета диссипативных свойств системы (μ
у
= 0) будет
m x c x y F F t
x y cm m
′′
+ − = − −( ) ( ).
Продифференцировав по времени последнее уравнение, получим
m x c x y F t
x y m
′′′
+
′
−
′
= −
′
( ) ( ).
Из этого уравнения
′
−
′
= −
′′′
−
′
x y
m
c
x
F t
c
x
y
m
y
( )
.
Здесь x”′- производная ускорения, или рывок, характеризующий скорость изменения
ускорения, или скорость изменения возмущающего воздействия, приложенного к машине,
мс
-3
.
Обозначим x”′=
′
a
x
, тогда из уравнения (5.15), для демпфирования колебаний на
канате при торможении, тормозное усилие должно формироваться по закону
176
176

F t F t
к
c
m a F t
p m
у
y
x x m
( ) ( ) ( ( ).= + −
′
−
′
(5.16)
Переходный процесс режима торможения с системой автоматического регулирования,
построенной по принципу формирования тормозного усилия по закону (5.16), аналогичен
процессу, приведенному на рис. 5.11.
Таким образом, взяв в качестве параметров измерения ускорение машины и тормозное
усилие, получим надежные сигналы, необходимые для формирования усилия, которое
обеспечит демпфирование колебаний сосуда на канате.
Реализация систем автоматического демпфирования колебаний позволит снизить
уровень динамических нагрузок и, тем самым, увеличить безопасность и долговечность
эксплуатации машин.
5.7. ДИНАМИЧЕСКИЕ ПОГЛОТИТЕЛИ КОЛЕБАНИЙ
Машины, на которые действуют переменные силы с постоянной частотой,
испытывают вредные колебания, особенно вблизи резонанса. В практике эксплуатации
таких машин для снижения амплитуды колебаний, как было показано в разделе 3.4,
стремятся удалиться от резонанса, путем изменения жесткости и массы (частоты свободных
колебаний). Иногда встречаются случаи, когда такое решение оказывается непрактичным.
Для решения этой задачи в 1909 г. Фрамом был изобретен динамический поглотитель
колебаний [39]. Чтобы пояснить принцип работы поглотителя колебаний, представим
механическую систему с двумя степенями свободы схемой, приведенной на рис. 5.12.
Рис. 5.12 Динамический поглотитель колебаний
Если на массу m
1
действует гармоническая сила S sin kt с частотой k, то оказывается, можно
подобрать массу m
2
и жесткость пружины с
2
таким образом, что масса m
1
не будет
совершать колебаний. Это, очевидно, можно получить тогда, когда сила упругости F
y2
будет равна и противоположно направлена возмущающей силе S sin kt. Практически
достигнуть полного поглощения колебаний массы m
1
невозможно. При отсутствии
колебаний массы m
1
, последняя не будет передавать усилие пружине жесткостью с
2
и, как
следствие, масса m
2
останется неподвижной. Для доказательства работоспособности
динамического поглотителя колебаний составим математическую модель, рассматриваемой
схемы. Эта схема представляет частный случай схем, приведенных на рис. 3.1 и 4.1.
Поэтому по аналогии с 4.1, принимая пружины чисто упругими элементами, запишем
y
1
F
m
1
y
2
c
1
y
c
F
2
2
F
2
2
y
m
1
S s i n k t
y
177
177

m y S kt F F
m y F
F c y
F c y y
y y
y
y
y
1 1 1 2
2 2 2
1 1 1
2 2 1 2
′′
= − −
′′
=
=
= −
sin ,
,
,
( ).
Систему уравнений представим
m y c c y c y S kt
m y c y y
1 1 1 2 1 2 2
2 2 2 2 1
0
′′
+ + − =
′′
+ − =
( ) sin ,
( ) .
(5.17)
При изучении колебательных процессов механических систем с одной и с двумя степенями
свободы при гармонической возмущающей силе было отмечено, что свободные колебания
быстро затухают и в системе присутствуют только вынужденные колебания (рис. 3.11 и
4.11, а). Вынужденные колебания характеризуются уравнением (4.56), в котором при
отсутствии сил вязкого демпфирования (μ
2
= 0) постоянная M = 0 и, следовательно
y A kt
y A kt
1 1
2 2
=
=
sin ;
sin .
Здесь A
1
и A
2
- амплитуды колебаний масс m
1
и m
2
.
После двукратного дифференцирования этих выражений и подстановки в уравнение
(5.17) получим зависимости, в которых все члены пропорциональны величине sin kt.
Сократив эту величину, получим систему алгебраических уравнений
( ) ,
( ) .
c c m k A c A S
c A m k c A
1 2 1
2
1 2 2
2 1 2
2
2 2
0
+ − − =
+ − =
(5.18)
Под действием силы S, пружина жесткостью c
1
будет иметь статическую деформацию
y
S
c
ст
=
1
, поэтому, разделив уравнение (5.18) на c
1
и, введя обозначения:
ω
1
1
1
=
с
m
и
ω
2
2
2
=
с
m
, получим
( ) ,
( ) .
1
1
2
1
2
1
2
1
2
1
2
1
2
2
2
2
+ − − =
= −
c
c
k
A
c
c
A y
A
k
A
ст
ω
ω
где ω
1
и ω
2
- собственные частоты колебаний масс m
1
и m
2
, c
-1
.
Если ввести понятия относительных амплитуд
A
A
y
A
A
y
ст ст
1
1
2
2
= =и
, то получим
178
178

A
k
k
c
c
k
c
c
A
k
c
c
k
c
c
1
2
2
2
2
2
2
2
1
2
1
2
2
1
2
2
2
2
2
1
2
1
2
2
1
1
1 1
1
1 1
=
−
− + − −
=
− + − −
ω
ω ω
ω ω
( )( )
,
( )( )
.
(5.19)
Из первого уравнения системы (5.19) видно, что относительная амплитуда колебаний
массы m
1
будет равна нулю при условии, если числитель
1 0
2
2
2
− =
k
ω
.
Следовательно, если собственная частота колебаний поглотителя равна частоте колебаний
возбуждающей силы, то колебания массы m
1
будут отсутствовать. Рассмотренный
динамический поглотитель колебаний может быть настроен только на одну частоту и
применение его ограничено машинами, работающими с постоянной скоростью.
Подбор параметров поглотителя осуществляется из соотношения
c
m
k
2
2
2
= .
(5.20)
Аналогичные явления происходят и в крутильной системе, состоящей из двух
маховых масс с моментами инерции J и J
1
(рис. 5.13).
Рис. 5.13. Динамический поглотитель крутильных колебаний
Предположим, J это момент инерции синхронного электродвигателя, вращающегося с
постоянной скоростью. Рабочая машина с моментом инерции J
1
соединена с
электродвигателем трансмиссией и имеет крутильную жесткость c
1
. Если момент
сопротивления характеризуется гармонической функцией с частотой k, то в валопроводе
жесткостью c
1
, будут наблюдаться колебания. В соответствии с вышерассмотренным,
можно подобрать дополнительную массу с моментом инерции J
2
и присоединить ее с
помощью валопровода жесткостью c
2
к маховой массе J
1
. Если параметры динамического
поглотителя крутильных колебаний выбраны с соблюдением соотношения
c
J
k
2
2
2
= ,
то машина будет работать без колебаний.
J
J
J
1
2
1
2
c
c
179
179

Пример 5.3. На рабочую машину (рис. 5.12), имеющую массу m
1
= 1000 кг, действует
гармоническая сила S = 1кН, с частотой k = 10 с
-1
. Жесткость валопровода c
1
= 100 кН м
-1
.
Определить параметры поглотителя и исследовать режим работы механической системы с
динамическим поглотителем.
Механическая система без динамического поглотителя эквивалентна схеме,
изображенной на рис. 3.1. Частота свободных колебаний массы m
1
равна
ω
1
1
1
10= =
c
m
c
-1
.
.
На массу m
1
действует гармоническая сила с частотой k = 10 с
-1
. Следовательно,
механическая система будет работать в резонансном режиме. Если предположить, что в
системе имеются диссипативные силы, соответствующие коэффициенту μ
1
= 0,1ω
1
, то
согласно рис. 3.12 амплитуда колебаний массы m
1
будет в пять раз больше статической
деформации. Статическая деформация пружины с жесткостью с
1
под действием силы S
равна
y
S
c
ст
= = ⋅
−
1
2
1 10 м.
Из рис. 3.13 видно, что для получения относительной амплитуды равной 0,2 - 0,3
необходимо увеличить частоту возмущающей силы в два - три раза. Этот же результат
можно получить за счет применения динамического поглотителя колебаний.
В соответствие с (5.20) жесткость и масса поглотителя связаны соотношением
с k m
2
2
2
=
Существует бесконечное количество параметров поглотителя, которые удовлетворяют это
соотношение, поэтому при их выборе необходимо руководствоваться конструктивными
соображениями. Следует помнить, что при уменьшении массы m
2
уменьшается жесткость и,
как следствие, будет увеличиваться перемещение массы m
2
.
Рассмотрим два варианта поглотителя, имеющего массу m
2
.= 1000 кг.
′
m
2
=100 кг.
Жесткости пружин, обеспечивающие частоту свободных колебаний k = 10 с
-1
будут
c k m
2
2
2
100= = ⋅кН м
-1
,
c
2
10
∗
= ⋅кН м
-1
.
Для исследования режима работы динамического поглотителя воспользуемся системой
дифференциальных уравнений (5.17).
Предположим, в системе присутствуют силы вязкого сопротивления, которые
характеризуются коэффициентами μ
y1
и μ
y2
. Связь этих коэффициентов с коэффициентом μ
i
= 0,1ω
i
выражается соотношением
µ
µ
i
y
i
m
=
1
2
1
.
Тогда силы упругости F
y1
и
F
y2
запишутся
F c y y F c y y y y
y y y y1 1 1 1 1 2 2 1 2 2 1 2
= +
′
= − +
′
−
′
µ µ, ( ) ( ).
С учетом этого система дифференциальных уравнений (5.17) будет
m y c c y c y y y S kt
m y c y y y y
y y y
y
1 1 1 2 1 2 2 1 2 1 2 2
2 2 2 2 1 2 2 1
0
′′
+ + − + +
′
−
′
=
′′ + − + ′ − ′ =
( ) ( ) sin ,
( ) ( ) .
µ µ µ
µ
180
180
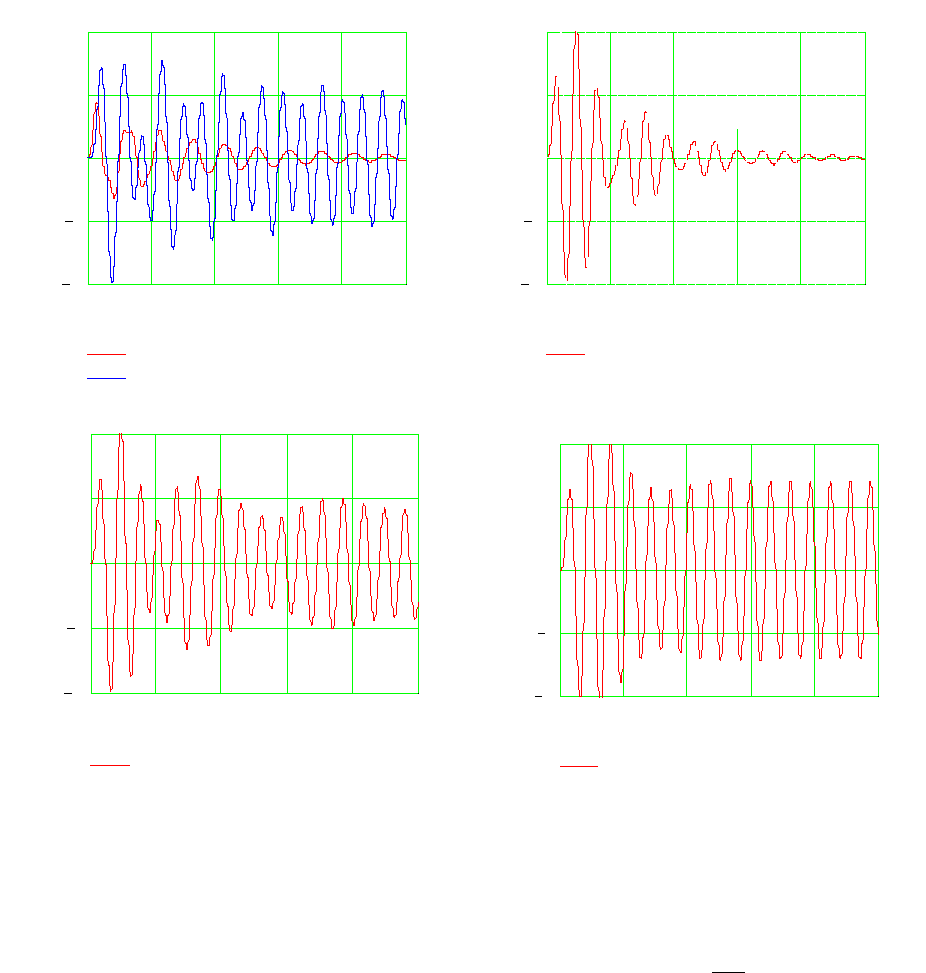
Полученная система дифференциальных уравнений решена с помощью пакета Mathcad 7.0.
0 2 4 6 8 10
2
1
0
1
2
m1=1000 êã
m2=1000 êã
a
âðåìÿ. ñ
Yîòí
.
0 2 4 6 8 10
2
1
0
1
2
m1=1000 êã
m2=100 êã
á
âðåìÿ. ñ
Yîòí
.
0 2 4 6 8 10
2
1
0
1
2
m1=1000 êã
m2=110 êã
â
âðåìÿ. ñ
Yîòí
.
0 2 4 6 8 10
2
1
0
1
2
m1=1000 êã
m2=100 êã ñ äåìïôåðîì
ã
âðåìÿ. ñ
Yîòí
.
Рис. 5.14. Характеристики переходных процессов с динамическими поглотителями
Подтверждено, что при отсутствии упругой связи между массами m
1
и m
2
система работает
в резонансном режиме и относительная амплитуда перемещения
( )y
y
y
ст
i
ст
=
равна 5,
которая достигает этой величины через 4 с после начала процесса.
На рис. 5.14, а и б показаны динамические процессы при работе машины с
поглотителем колебаний. Видно, что при m
2
= 1000 кг, относительное перемещение массы
m
1
через 6 с не превышает величины равной 0,2, которое в дальнейшем уменьшается. При
этом амплитуда относительного перемещения массы m
2
превышает единицу. Во втором
случае (m
2
= 100 кг) снижение амплитуды колебаний до величины 0,2 происходит за такое
же время, однако, в первоначальный момент она достигает двух единиц. Амплитуда
относительного перемещения массы m
2
равна 5 (на графике не показана). Таким образом,
поглотители колебаний с массами 1000 и 100 кг позволяют получить один и тот же
результат, поэтому окончательное решение принимается с учетом конструктивных
соображений, учитывая то обстоятельство, что с уменьшением массы m
2
увеличивается
181
181
