Stefanica D. A Primer for the Mathematics of Financial Engineering
Подождите немного. Документ загружается.


144
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
Theorem
5.1.
(Derivative
form
of
the
Taylor
approximation
er-
ror.)
Let
f
(x)
be
a
function
which
is n + 1
times
differentiable,
and
assume
that
f(n+l)(x)
continuous.
Let
f(x)
-
Pn(x)
be
the
approximation
error
of
f
(x)
by
the
n-th
order Taylor
polynomial
P
n
(x).
Then, there exists a
point
c
between a
and
x
such
that
f (
x)
- P
n
(
x)
can
be
express ed as
( )n+l
f(x)
-
Po
(x)
= x - a
f(n+l\c).
n
(n+1)!
(5.3)
The
proof
of
this
theorem
uses Rolle's
theorem,
and
is
beyond
our
scope.
Note
that,
for n = 0,
Theorem
5.1
becomes
the
Mean
Value
Theorem.
Theorem
5.2.
(Integral
form
of
the
Taylor
approximation
error.)
If
f(x)
is a
function
which is n + 1
times
differentiable,
and
if
f(n+l)
(x)
is
continuous,
then
the
n-th
order
Taylor
approximation
error
f(x)
-
Pn(x)
can
be
expressed as the following integral:
Proof.
We
give a
proof
by
induction:
For
n = 0, formula (5.4)
becomes
f(x) -
Fa(x)
= [ f'(t)
dt.
Since P
(0)
= f ( a ),
this
is a
direct
consequence
of
the
Fundamental
Theorem
of
; cf.
Theorem
1.4.
For
the
induction
step,
we
assume
that
formula
(5.4) holds for n, i.e.,
(5.5)
and
prove
that
(5.4) also holds for n + 1, i.e,
x -
(n+2)
l
x
(
t)n+l
f(x)
- P
n
+
1
(x)
= a
(n
+ 1)! f (t) dt.
(5.6)
Using
integration
by
parts,
the
term
J:
((~2;)~1
f(n+2)(t)
dt
can
be
written
as
(x
- t)n+l f(n+l)(t)l
t
=x
_
{X
~
((x
-
t)n+l)
f(n+l)(t)
dt
(n
+ 1)!
t=a
Ja
dt
(n
+ 1)!
(x
- a)n+l f(n+l) (a) +
{X
(x
,t)n
f(n+l)(t) dt.
(n+1)!
Ja
n.
5.1.
TAYLOR'S
FORMULA
FOR
FUNCTIONS
OF
ONE
VARIABLE
145
Then,
from
the
induction
hypothesis
(5.5),
it
follows
that
[
(x
- t)n+l f(n+2)(t)
dt
(n
+ 1)!
( )n+l
X - a f(n+l) (a) +
(f(x)
-
Pn(x))
(n
+ 1)!
f(x)
-
(Po
(x)
+
(x
- a)n+l f(n+l)
(a))
n
(n+1)!
.
From
(5.1),
it
is
easy
to
see
that
We
conclude
that
which is
the
same
as
(5.6).
This
completes
the
proof
by
induction.
D
The
order
of
approximation
of
a
function
by
its
Taylor
polynomials
can
be
obtained
using
the
derivative form for
the
Taylor
approximation
error
(5.3).
Theorem
5.3.
Let
f(x)
be
a
function
which is
n+1
times
differentiable,
and
assume
that
f(n+l)
(x)
is a
continuous
function.
Then,
the
approximation
of
f(x)
by
the
n-th
order
Taylor
polynomial
is
of
order
n + 1, i.e.,
f(x) = f(a) + (x a)f'(a) + (x
~
a)2
f"(a) + ... + (x :,a)n
f(n1(a)
+ 0
((x
- a)n+l) , as x
---7
a. (5.7)
Proof.
Let
Pn(x)
=
L:~=o
(x~~)k
f(k)(a)
be
the
n-th
order
Taylor
polynomial
corresponding
to
f(x);
cf.
(5.1).
Then
(5.7)
can
be
written
as
f(x)
=
Pn(x)
+ o
((x_a)n+l)
,
as
X---7
a. (5.8)
Recall
from
definition (43)
that
(5.8) is equivalent
to
proving
that
1
·
If(x)
Pn(x)
I
1m
sup
I I 1
x-faX
- a
n+
<
00.
To show
this,
consider a fixed
interval
[a
r, a +
r]
around
a,
and
let
M =
max
If(n+l)(z)l.
zE[a-r,a+r]
(5.9)
Note
that
M <
00,
since
the
function
f(n+l)(x) is
continuous.

146
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
Let
x E
[a
- r, a +
r].
From
the
derivative form (5.3) for
the
Taylor
residual, we know
that
there
exists a
point
c between a
and
x such
that
(
)n+l
f(x)-P,(x)
=
x-a
f(n+l)(c).
(5.10)
n
(n+l)!
Note
that,
if
c is between a
and
x
and
if x E [a-r, a+r],
then
c E [a-r, a+r].
From
(5.9)
and
(5.10), we find
that
If(x) - Pn(x) I If(n+I)(c)1 < M
Ix
-
al
n
+
l
(n
+ I)!
(n
+
I)!'
In
other
words,
Iff:~~0'J;)1
is
bounded
uniformly for all x E
[a
-
r,
a +
r],
and
therefore
1
.
If(x) -
Pn(x)1
1m
sup
I _
In+l
x--ta x a
<
00,
which is
what
we
wanted
to
prove.
D
From
Theorem
5.3, we
obtain
that
the
linear Taylor
approximation
f(x)
~
f(a) + (x - a)f'(a) (5.11 )
is a second
order
approximation, if
f"
(x)
is a continuous function:
f(x) = f(a) +
(x
- a)J'(a) + 0 ((x -
a?)
, (5.12)
as x ---7
a.
Also,
the
quadratic
Taylor
approximation
f(x)
~
f(a) +
(x
- a)f'(a) +
(x
~
a?
f"(a)
(5.13)
is a
third
order
approximation, if
f(3)
(x) is continuous:
(x
a)2
f(x) = f(a) +
(x
- a)J'(a) +
~
f"(a) + 0 ((x -
a)3)
, (5.14)
as x ---7
a.
The
exponential function,
the
natural
logarithm
function,
and
some sim-
ple
rational
functions
appear
frequently
in
financial applications.
The
follow-
ing linear
and
quadratic
Taylor
approximations
are often needed:
Linear
Approximations:
eX
~
1
+x;
(5.15)
In(l+x)
~
X'
, (5.16)
In
(1-
x)
~
-x;
(5.17)
1
1-
x;
(5.18)
~
l+x
1
(5.19)
~
1
+x.
1
x
5.2.
TAYLOR'S
FORMULA
FOR
MULTIVARIABLE
FUNCTIONS
147
Quadratic
Approximations:
eX
x
2
~
l+x+
2
;
(5.20)
In
(1
+ x)
x
2
~
X--'
(5.21 )
2'
In
(1
x)
x
2
~
-X--'
(5.22)
2'
1
1-
x + x
2
;
~
(5.23)
l+x
1
1
+ x + x
2
.
~
(5.24)
I-x
Note
that
these
approximations
are
accurate
only
for small values of x.
5.2
Taylor's
formula
for
multivariable
functions
Scalar
Functions
Let
f :
~n
---7
~
be
a function
of
n variables
denoted
by
Xl,
X2,
...
, x
n
.
Let x = (Xl,
X2,
...
,x
n
).
We present first
order
and
second
order
Taylor
expansions
of
the
function f (x),
without
providing convergence results.
Let a = (aI,
a2,
.
..
,an) E
~n.
The
linear Taylor
expansion
of
the
function
f (x)
around
the
point
a,
n
af
f(x)
~
f(a) +
tt(xi
-
ai)
ax/a),
(5.25)
is a second
order
approximation,
in
the
sense
that
as x ---7
a,
if
all
the
partial
derivatives
of
second
order
of
f(x)
i.e.
~(x)
,
'OXiOXj
,
1 ::; i, j
::;
n, are. continuous.
He~e,
0
(11x
-
a11
2
)
=
L:~=l
0
(IXi
-
ail
2
) .
The
quadratIc
Taylor expanSIOn
of
the
function f (x)
around
the
point
a,
n
af
f(x)
~
f(a) +
L(Xi
-
ai)
-(a)
i=l
aXi
+ "
(Xi
-
ai)~Xj
- aj) a
2
f
L.t
aXiaXj
(a),
l:5:i,j:5:n
(5.27)

148
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
is a
third
order
approximation,
in
the
sense
that
(5.28)
as x
~
a,
if all
the
third
order
partial
derivatives
of
f (x)
are
continuous.
The
linear
and
quadratic
Taylor expansions (5.25-5.28)
can
be
written
using
matrix
notation
as follows: Recall from (1.36)
that
the
gradient
D
f(x)
of
the
function f(x) is a row
vector
of
size
n,
i.e.,
(
a
f
af
a
f
)
Df(x)
=
-a
(x)
-a
(x)
...
-a
(x) ,
Xl
X2
Xn
and,
from (1.37),
that
the
Hessian
D2
f(x)
is
an
n x n matrix:
fJ2f(x)
8
2
f 8
2
f
8xi
8X28xl
(x)
8x
n
8
x
l (x)
8
2
f
8
2
f(x)
8
2
f
D2f(x)
8x
1
8
x
2 (x)
8x~
8x
n
8x
2 (x)
8
2
f
8
2
f
8
2
f (x)
8x
1
8x
n
(x)
8x
2
8x
n
(x)
8x;
Let
c,-a
,
)
X2
-
a2
(5.29)
x-a
. .
Xn
-
an
The
linear Taylor expansions (5.25)
and
(5.26)
of
f(x)
around
the
point
a
can
be
written
in
terms
of
the
gradient
D f (
a)
as
f(x)
~
f(a) + D f(a)
(x
-
a);
(5.30)
f(x) = f(a) +
Df(a)
(x
-
a)
+ 0
(11x
- aW) , (5.31)
as x
~
a.
The
quadratic
Taylor expansions (5.27)
and
(5.28) of f(x)
around
the
point
a
can
be
written
in
terms
of
D f (
a)
and
D2
f (
a)
as
1
f(x)
~
f(a) +
Df(a)
(x-a)+"2
(x-a)t
D2f(a)
(x-a);
(5.32)
5.2.
TAYLOR'S
FORMULA
FOR
MULTIVARIABLE
FUNCTIONS
149
1
f(x)
= f(a) + Df(a)
(x
-
a)
+"2
(x
- a)t
D2
f(a)
(x
-
a)
n
+ L 0
(IXi
-
ai
1
3
) ,
(5.33)
i=l
as x
~
a.
Note
that
(x
- a)t =
(Xl
-
a1
X2
-
a2
...
Xn
-
an)
is a row
vector,
the
transpose
of
the
column vector x - a from (5.29).
Vector Valued Functions
Let
F :
JRn
~
JRm
be
a vector valued function, given
by
F(x) =
(j~~~l),
fm(x)
where x =
(Xl,
X2,
...
, x
n
).
Recall from (1.38)
that
the
gradient
DF(x) of
F ( x) is a
matrix
operator
of
size m x n given
by
DF(x)
(
8il
(x)
8il
(x)
...
8il
(x) )
8~
8~
8~
812
(x)
812
(x)
...
812
(x)
8Xl
8X2
8x"
:
:.
:
..
.
8fm
(x)
8fm
(x)
8fm
(x)
8~
8~
8~
The
linear Taylor
expansion
of
the
function F(x)
around
the
point
a E
JRn,
F(x)
~
F(a) + DF(a) (x -
a)
(5.34)
is a second
order
approximation, i.e.,
F(x) = F(a) + DF(a)
(x
-
a)
+ 0
(11x
-
a11
2
) ,
(5.35)
as x
~
a,
if all
the
partial
order
derivatives
of
order
two
of
the
functions fk (x),
k =
1:
m,
are
continuous. As before,
O(llx-aI12)
= 2:7=10(lxi-aiI2),
and
x - a is
the
column
vector given
by
(5.29).
We
note
that
formula (5.34)
can
be
written
explicitely as
(
h(x)
) (
h(a)
+
2:~=1
~J~(a)
(Xi
-
ai)
)
h(x)
r-v
h(a)
+
2:i=l
8x,
(a)
(Xi
-
ai)
:
r-.J
: •
fm(x)
fm(a)
+
2:7=1
BJ;:(a)
(Xi
-
ai)
Thus,
the
linear Taylor
approximation
formula (5.34) for
the
vector valued
function F (x) is
obtained
by
combining
the
linear Taylor
approximation
for-
mula
(5.25) for
each
function fk(X), k = 1 :
m.
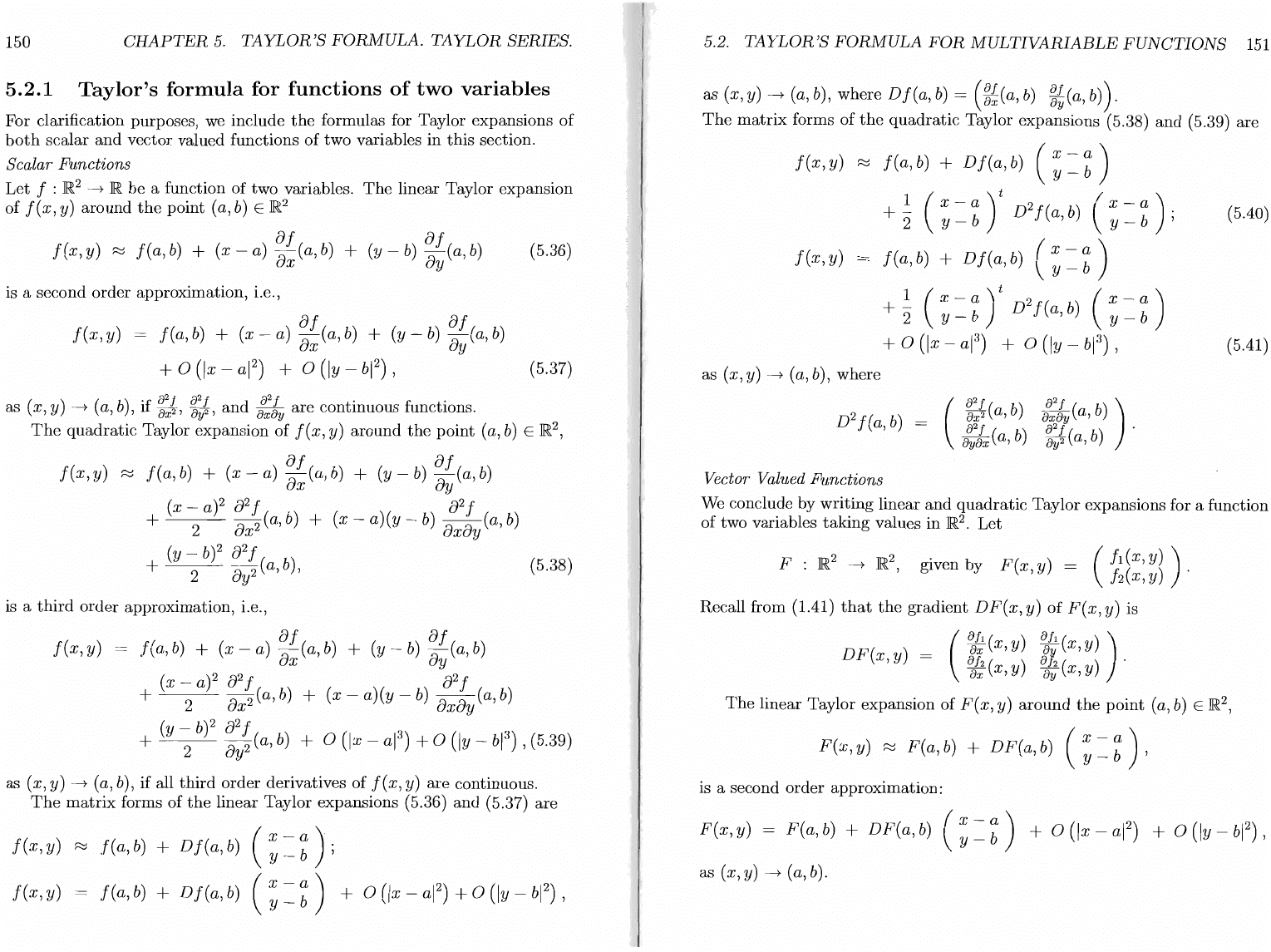
150
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
5.2.1
Taylor's
formula
for
functions
of
two
variables
For clarification purposes, we include
the
formulas for Taylor expansions
of
both
scalar
and
vector valued functions
of
two
variables
in
this
section.
Scalar Functions
Let
f : ]R2
----+
]R
be
a function
of
two variables.
The
linear Taylor
expansion
of
f(x,
y)
around
the
point
(a,
b)
E]R2
8f
8f
f(x,y)
~
f(a,b) +
(x-a)
8x(a,b) +
(y-b)
8y(a,b)
(5.36)
is a second
order
approximation, i.e.,
af
8f
f(x,
y)
= f(a,
b)
+
(x
-
a)
8x
(a,
b)
+
(y
-
b)
8y
(a,
b)
+ 0
(Jx
-
aJ2)
+ 0
(Jy
-
bJ2)
, (5.37)
•
{Pj
fJ2j fJ2j . .
as
(x,
y)
----+
(a,
b),
If
fJx
2
, fJy2'
and
fJxfJy
are
contInuous functIOns.
The
quadratic
Taylor expansion
of
f
(x,
y)
around
the
point
(a,
b)
E ]R2,
f(x,
y)
~
8f 8f
f (
a,
b)
+
(x
-
a)
8x
(
a,
b)
+
(y
-
b)
8y (
a,
b)
(x
-
a?
8
2
f 8
2
f
+ 8 2
(a,
b)
+
(x
-
a)
(y
-
b)
-8
a (
a,
b)
2 x x y
(y
-
b)2
8
2
f (
b)
+ 2
8y2
a,
,
(5.38)
is a
third
order
approximation, i.e.,
f(x,
y)
=
8f
af
f(a,
b)
+
(x
-
a)
8x
(a,
b)
+
(y
b)
ay
(a,
b)
(x
-
a)
2
8
2
f 8
2
f
+ a 2(a,b) +
(x
- a)(y -
b)
-8
8 (a,b)
2 x x y
+
(y
-
b)2
88
2
{
(a,
b)
+ 0
(Jx
-
aJ3)
+ 0
(Jy
-
bJ3)
,(5.39)
2 y
as (x, y)
----+
(a,
b),
if all
third
order
derivatives
of
f(x,
y)
are continuous.
The
matrix
forms
of
the
linear Taylor expansions (5.36)
and
(5.37)
are
f (x, y)
""
f (
a,
b)
+ D f (
a,
b)
(~-=
n ;
f(x,y)
f(a,b) +
Df(a,b)
(~-=n
+
O(lx-
a
I
2
)+O(ly-
b
I
2
),
5.2.
TAYLOR'S
FORMULA
FOR
MULTIVARIABLE
FUNCTIONS
151
as (x,
y)
----+
(a,
b),
where D f
(a,
b)
=
(~;
(a,
b)
~;
(a,
b)
) .
The
matrix
forms
of
the
quadratic
Taylor expansions (5.38)
and
(5.39) are
f (x, y)
RO
f (
a,
b)
+ D f (
a,
b)
(~-=
~
)
1
(x_a)t
2
(x-a)
+
2"
y - b D f (
a,
b)
y - b ;
(5.40)
f(x,
y) f(a,
b)
+
Df(a,
b)
(~-=
~
)
+
~
(~-=nt
J)2f(a,b)
(~-=n
+ 0
(Jx
-
aJ3)
+ 0
(Jy
-
bJ3)
,
(5.41 )
as
(x,
y)
----+
(a,
b),
where
Vector Valued Functions
We conclude
by
writing
linear
and
quadratic
Taylor expansions for a function
of
two variables
taking
values
in
]R2.
Let
F : ]R2
--;
]R2, given
by
F(x,y)
=
(~~i~:;j).
Recall from (1.41)
that
the
gradient
DF(x,
y)
of
F(x,
y)
is
DF(
)
=
(r:J;(X,y)
~(X,y))
X,y
fJ
h
()
fJ
h
( ) .
ax
x,
y
ay
x,
y
The
linear Taylor expansion
of
F(x,
y)
around
the
point
(a,
b)
E ]R2,
F(x,y)
RO
F(a,b) + DF(a,b)
(~-=
~
) ,
is a second
order
approximation:
F(x,y)
= F(a,
b)
+ DF(a,b)
(~-=
~)
+ 0
(Ix
-
a1
2
)
+ 0
(Iy
-
b1
2
) ,
as
(x,
y)
----+
(a,
b).
152
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
5.3
Tay
lor
series
expansions
When
discussing
the
approximation
properties
of
Taylor polynomials
in
sec-
tion
5.1, we assumed
that
the
function
f :
JR
---+
JR
is differentiable a finite
number
of times.
If
the
function f (x) is infinitely
many
times
differentiable,
then
we
can
define
its
Taylor series
expansion
as
(
)
_
~
(x - a)kf(k)( )
T x -
~
k!
a.
k=O
Recall from (5.2)
that
Pn(x) =
2:~=0
(x~~)k
f(k)(a),
and
therefore
T(x)
= lim Pn(x).
n-7OO
(5.42)
(5.43)
In
other
words,
the
Taylor series expansion
of
the
function f
(x)
can
also
be
viewed as
the
limit
of
the
Taylor polynomials P
n
(x) corresponding
to
f (x),
as
the
degree n goes
to
infinity
(at
all
points
x where
this
limit exists).
Deciding
when
does
the
Taylor series
T(x)
converge
to
the
function
f(x),
i.e., finding x such
that
T(x)
=
f(x),
is
rather
subtle.
Example:
The
function
f ( x ) -
{ex
p
( -
;2),
if
x # °
- 0,
if
x = °
is infinitely
times
many
differentiable
at
all points, including
at
x = 0,
and
Then,
the
Taylor series expansion of f (x)
around
the
point
a = ° is identically
equal
to
zero, i.e.,
00
k
T(x)
= L
:!
/k)(O) = 0,
\;j
x E
JR.
k=O
Therefore,
the
Taylor expansion T (x) is different
than
f (x)
at
all
the
points
x#O.
D
Note
that
the
Taylor series
T(x)
is a power series
of
the
form (4.29), i.e.,
00
T(x)
= L ak(x - a)k,
k=O
f(k)
(a)
with
ak
=
-k-!-'
\;j
k
~
0.
A
practical
way
of
computing
the
radius
of
convergence
of
a Taylor series,
and
therefore of finding
the
convergence
domain
of
the
series, is given
in
5.3.
TAYLOR
SERIES
EXPANSIONS
153
Theorem
5.4. Before
stating
this
theorem, we recall
that,
given a sequence
(Xn)n=l:oo
of
real
numbers,
lim
infn-7oo
Xn
is defined
as
the
smallest value l for
which
there
exists a subsequence of
(Xn)n=l:oo
converging
to
l.
Note
that,
if
lim
Xn
exists,
then
lim inf
Xn
= lim x
n
.
n--+oo
n--+oo
n-7OO
(5.44)
Also, if all
the
terms
of
the
sequence
(Xn)n=l:oo
are
positive numbers, i.e., if
Xn
> ° for all n
~
1,
then
1 =
liminf~.
lim
sUPn--+oo
Xn
n--+oo
Xn
(5.45)
Theorem
5.4.
Let
f(x)
be
an
infinitely
many
times
differentiable
function,
and
let
T(x)
= 2::0
fC~!(a)(x
- a)k
be
the
Taylor
series
expansion
of
f(x)
around
the
point
a.
The
radius
of
convergence
ofT(x)
is
given
by
(5.46)
(5.47)
Proof.
By
definition (4.33),
the
radius
of
convergence R
of
the
Taylor series
T(
)
_",,00
fCk)(a)
(
)k··
b
x -
L..tk=O
-k!-
X - a
IS
gIven y
Then,
from (5.45),
it
follows
that
Using (4.37), we find
that
I
k!
Il/k
li~~f
f(k)(a)
..
( k )
((k!)l/k)
h~~f
If(k)(a)ll/
k
.
-k-
1 k
lim
inf
-,----,----,-
e
k--+oo
If(k)(a)ll/
k
·
(5.48)
(5.49)
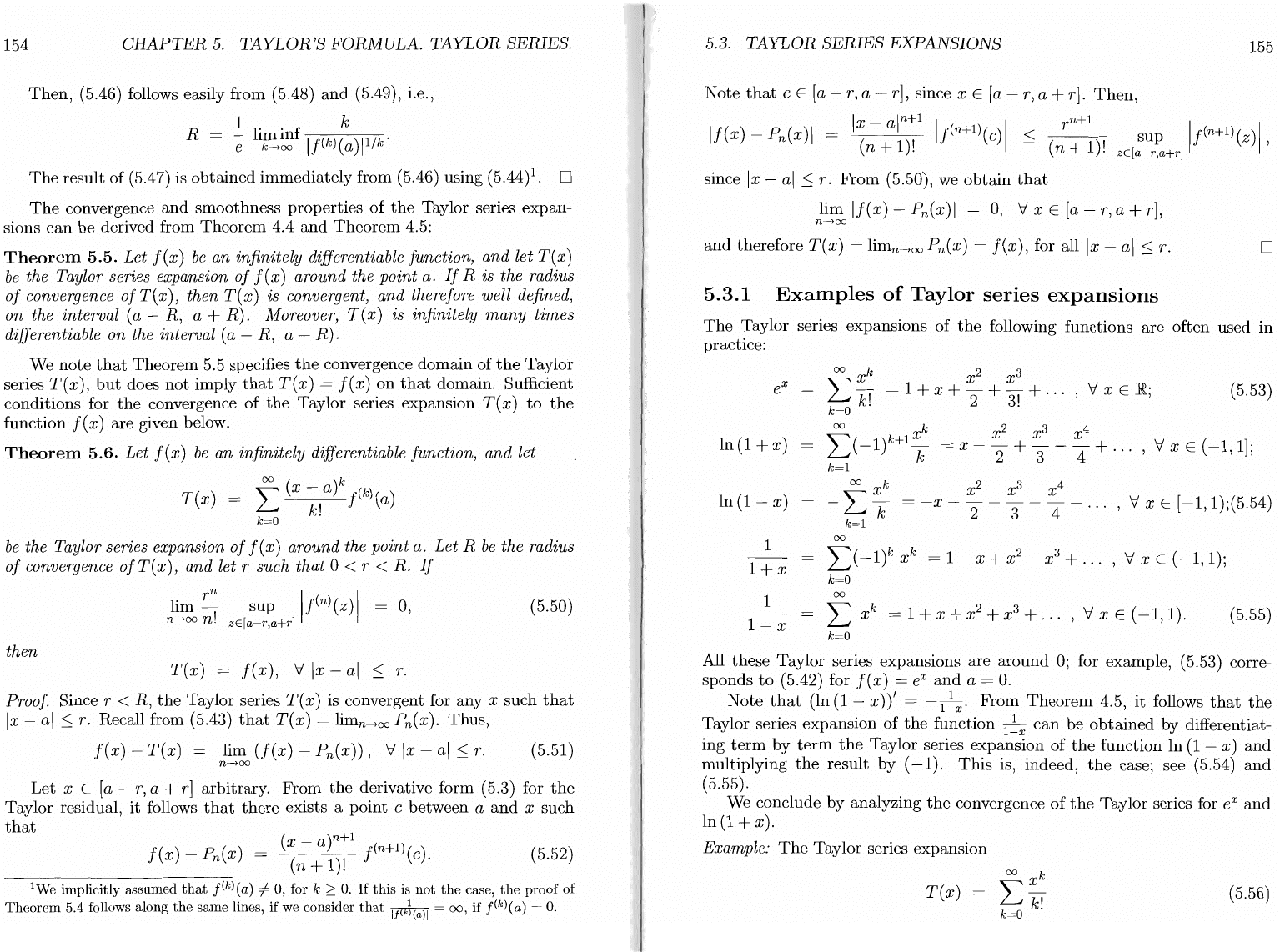
154
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
Then,
(5.46) follows easily from (5.48)
and
(5.49), i.e.,
1
..
k
R =
~
he~f
If(k)(a)1
1
/
k
'
The
result
of
(5.47) is
obtained
immediately
from (5.46) using (5.44)1. D
The
convergence
and
smoothness
properties
of
the
Taylor series
expan-
sions
can
be
derived from
Theorem
4.4
and
Theorem
4.5:
Theorem
5.5.
Let
f(x)
be
an infinitely differentiable function, and let
T(x)
be
the Taylor series expansion
of
f (x) around the point a.
If
R is the radius
of
convergence
of
T(
x),
then
T(
x) is convergent, and therefore well defined,
on the interval
(a
- R, a + R). Moreover,
T(x)
is infinitely
many
times
differentiable on the interval
(a
- R, a + R).
We
note
that
Theorem
5.5 specifies
the
convergence
domain
of
the
Taylor
series
T(x),
but
does
not
imply
that
T(x)
=
f(x)
on
that
domain. Sufficient
conditions for
the
convergence
of
the
Taylor series expansion
T(x)
to
the
function
f (x)
are
given below.
Theorem
5.6.
Let
f(x)
be
an infinitely differentiable function, and let
T(x) = f
(x
~!a)k
jlk)
(a)
k=O
be
the Taylor series expansion
of
f(x)
around the point
a.
Let R
be
the radius
of
convergence
of
T(
x),
and let r such that 0 < r <
R.
If
lim
rn
sup
If(n)(z)1 = 0,
n--too
n!
zE[a-r,a+r]
(5.50)
then
T(x)
=
f(x),
V
Ix
-
al
::;
r.
Proof. Since r < R,
the
Taylor series
T(
x) is convergent for
any
x such
that
I x - a I
::;
r.
Recall from (5.43)
that
T (x) =
limn--too
P
n
(
X
).
Thus,
f(x)
-
T(x)
= lim
(f(x)
- Pn(x)) , V
Ix
-
al
::;
r.
(5.51)
n--too
Let
x E
[a
-
r,
a +
r]
arbitrary.
From
the
derivative form (5.3) for
the
Taylor residual,
it
follows
that
there
exists a
point
c between a
and
x such
that
( )
n+1
f(x)-Po(x)
=
x-a
f(n+1)
(c)
n
(n+1)!
.
(5.52)
----------------------
1 We implicitly assumed
that
f(k) (a)
=I
0, for k
:::::
O.
If
this
is
not
the
case,
the
proof of
Theorem
5.4 follows along
the
same lines, if we consider
that
If(k5(a)1
=
00,
if f(k)(a) =
O.
5.3.
TAYLOR
SERIES EXPANSIONS
155
Note
that
c E
[a
- r, a +
r],
since x E
[a
- r, a +
r].
Then,
I
In+1
n+1
If
(x) -
Po
(x) I = x - a
If
(n+
1
) (
c)
I < r
su
p I
f(n+
1
) (z ) I '
n (n+1)! -
(n+1)!
zE[a-r,a+r]
since
Ix
-
al
::;
r.
From
(5.50), we
obtain
that
lim
If(x)
- Pn(x) I =
0,
V x E
[a
- r, a +
r],
n--too
and
therefore
T(x)
=
limn--too
Pn(x) =
f(x),
for all
Ix
-
al
::;
r.
D
5.3.1
Examples
of
Taylor
series
expansions
The
Taylor series expansions
of
the
following functions
are
often used
in
practice:
In(1
+
x)
In
(1
-
x)
1
1+x
1
1-x
00
k
-
L~
=-x
2
3 4
, V x E
[-1,
1); (5.54 )
k=1
00
"'(_1)k
xk 2 3
L...t
=
1-
x + x - x + ... , V x E
(-1,1);
k=O
00
L xk = 1 + x + x
2
+ x
3
+ .
..
, V x E
(-1,
1).
k=O
(5.55)
All
these
Taylor series expansions are
around
0; for example, (5.53) corre-
sponds
to
(5.42) for
f(x)
=
eX
and
a =
O.
Note
that
(In
(1
x))' =
-l~x'
From
Theorem
4.5,
it
follows
that
the
Taylor series expansion
of
the
function
l~x
can
be
obtained
by differentiat-
ing
term
by
term
the
Taylor series expansion
of
the
function In
(1
-
x)
and
multiplying
the
result
by
(-1).
This
is, indeed,
the
case; see (5.54)
and
(5.55).
We conclude
by
analyzing
the
convergence
of
the
Taylor series for
eX
and
In(1+x).
Example:
The
Taylor series expansion
00
k
T(x)
=
L%,
k=O
(5.56)
156
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
of
the
function f ( x) =
eX
is convergent for all x E
JR.
Proof: We first check
that
the
expansion (5.56) is correct.
It
is easy
to
see
that
f(k)(x) =
eX,
for all k
~
o.
Then
f(k)(O) = 1, for all k
~
0,
and
the
Taylor series expansion of f ( x)
around
the
point
a = 0 is
00
(k) ( )
00
k
T(
)
=
'\:'
~
k =
'\:'
~
x L..t
k!
x L..t
k!
.
k=1 k=1
From
(5.47) of
Theorem
5.4, we
obtain
that
the
radius of convergence
of
the
series T (
x)
is
1 k
R = - lim = lim k =
00.
e
k-+oo
If(k)(O)l
l
/
k
k-+oo
We conclude
that
T(
x)
is convergent for
any
x E
JR;
cf.
Theorem
4.4.
We use
Theorem
5.6
to
show
that
f(x)
=
T(x)
for any x E
JR.
Let r > 0
be
a fixed
arbitrary
positive number. Note
that
sup If(n)(x)1
xE[-r,
r]
Using (1.31), we conclude
that
sup
eX
= e
r
.
-rs,xs,r
rn
( ) . rn r
r.
rn
lim
-,
sup
If
n (x) I =
hm
- e = e
hm
- =
o.
n-+oo
n.
XE[-r,
r]
n-+oo
n!
n-+oo
n!
Thus,
the
convergence condition (5.50) is satisfied for any r >
O.
From
Theorem
5.6,
it
follows
that
f(x)
=
T(x)
for
any
real
number
x, i.e.,
00
k
eX
= L
~!'
V x E
JR.
D
k=O
Example:
The
Taylor series expansion
00
k
T(x)
=
L(
_l)k+l
~
,
k=1
(5.57)
of
the
function In
(1
+ x) is convergent
to
In
(1
+ x) for
any
x E
[-0.5,0.5].
Proof: We first check
that
the
expansion (5.57) is correct. Let
f(x)
=
In
(1
+
x).
It
is easy
to
see, e.g., by induction,
that
(_l)k+l
(k - I)!
f(k)(x) = V k
~
1.
(1
+ x)k
(5.58)
5.3.
TAYLOR
SERIES
EXPANSIONS
157
Then,
f(k)(O) =
(-l)k+l(k
- I)!, for all k
~
1.
Since f(O) =
In(l)
= 0,
it
follows
that
the
Taylor series of f (x)
around
the
point
a = 0 is
T(x)
=
~
f(k)(O) xk =
~
(_l)k+l
(k - I)! k =
~
(_l)k+l k
L..t
k!
L..t
k!
x L..t k
x,
k=1 k=1
k=1
which is
the
same
as (5.57).
The
series
T(
x)
can
be
written
as a power series as follows:
00
(
_l)k+l
with
ak
= , V k
~
1.
k
T(x)
= L akxk,
k=1
Recall from (1.29)
that
limk-+oo
k
l
/k
=
1.
Therefore,
lim
lakl
l
/
k
= lim
(~)
l/k = lim
_1_
=
1,
k-+oo
k-+oo
k
k-+oo
k
l
/k
From
Lemma
4.9,
it
follows
that
the
radius
of
convergence of
T(x)
is
1
R =
r·
I 1
1
/
k
=
1.
Imk-+oo
ak
A
We conclude from
Theorem
4.4
that
T(x)
is convergent if
Ixl
<
1,
and
that
T (
x)
is
not
convergent if I x I >
1.
We now use
Theorem
5.6
to
find points x where
T(x)
=
f(x).
Let 0 < r <
1.
From
(5.58), we find
that
sup
If(n)(x)1
xE[-r,
r]
Therefore,
(n
- I)!
sup
-rs,xs,r
(1
+ x)n
rn rn
(n - 1)'
lim -
sup
If(n) (x) I = lim - .
n-+oo
n!
xE[-r,
r]
n-+oo
n!
(1
- r)n
If
r
::;
~,
then
l:r
::;
1
and
we
obtain
that
rn
lim 1
sup
If(n)(x)1 =
O.
n-+oo
n.
xE[-r,
r]
(n
- I)!
(l-r)n·
The
convergence condition (5.50) is satisfied in
this
case. From Theorem 5.6,
it
follows
that
f(x)
=
T(x),
for
any
x
with
Ixl
::;
~,
i.e.,
00
k 1
In(l
+
x)
=
L(
_l)k+l
~,
V
Ixl
::;
2
k=1
(5.59)

158
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
The
result of
Theorem
5.6 is
not
strong
enough
to
prove
that
(5.59) also
holds
2
if
~
<
Ixl
<
1.
To
do
so,
the
Taylor
app~oximation
:rror.must
be
es~i
mated
using
the
integral form (5.4);
more
detaIls
are
provIded In
an
exerCIse
at
the
end
of
the
chapter. D
FINANCIAL
APPLICATIONS
Connections between
the
Greeks using Taylor's formula.
Approximation
of
the
Black-Scholes formula for
at-the-money
options.
Connections between
the
duration
and
convexity
of
a bond.
5.4
Connections
between
the
Greeks
using
Taylor's
formula
Let
V(S, t)
be
the
value
at
time
t
of
a
European
plain
.vanill~
op~ion
on
an
underlying asset
with
spot
price
S.
Recall
that
V(S,
t)
IS
an
Infimtely
many
times
differentiable function
in
both
variables
Sand
t.
To
write
the
quadratic
Taylor expansion of V(S,
t)
around
the
point
(S,
t)
we use (5.39) for a =
S,
b =
t,
x = S + dS,
and
y = t + dt,
and
obtain
that
v (S +
dS,
t + dt)
av
av
V(S,
t)
+ dS
as
+
dtat
(dS)2
a
2
v
(dt?
a
2
v
+
-2-
aS
2
+
-2-
8t
2
a
2
v
+ (dS)(dt)
asat
+
O(
(dS)3) + O((dt)3).
(5.60)
For
the
discretized evolution model
of
the
price
of
the
underlying asset
to
converge
to
a lognormal model,
the
following condition
must
be
satisfied:
(dS?
~
O'2S2dt.
LetdV
=
V(S
+
dS,
t + dt) - V(S, t).
If
we ignore all
the
terms
of
order
larger
than
dt from (5.60), we find
that
av av
(dS?
a
2
v
dV
~
as
dS +
at
dt +
-2-
aS
2
-------------------=~-
2We
also
note
that
f(
-1)
and
T(
-1)
are
not
defined,
and
that
T(l)
=
f(l):
00
( l)k+1
T(l)
= L
~
= In(2) =
f(l).
k=l
5.4.
GREEKS
AND
TAYLOR'S
FORMULA
Recall
that
~
= av
as'
av
and
e =
at.
Then,
the
approximate
formula (5.61)
can
be
written
as
O'2S2
dV
~
~
dS + e dt +
--r
dt
2 '
or, equivalently,
O'2S2
dV
-
~
dS
~
e dt +
-2-r
dt.
159
(5.61)
(5.62)
For simplicity, assume
that
the
underlying asset does
not
pay
dividends.
To hedge a
long
position
in
the
derivative security, a
short
position
in
~
units
of
the
underlying
asset
must
be
taken.
If
IT
is
the
value
of
the
resulting
portfolio,
then
IT
= V -
~S.
Note
that
if
the
value
of
the
underlying asset
changes from S
to
S
+dS,
then
the
value
of
the
portfolio changes as follows
3
:
dIT
IT(S + dS) -
IT(
S)
(V(S
+ dS) -
~(S
+ dS))
(V(S)
-
~S)
V(S
+ dS) -
V(S)
-
~dS
dV
-
~dS.
Then,
(5.62) becomes
(5.63)
The
reason
for
shorting
~
units
of
the
underlying asset
in
the
portfolio is
to
make
the
value
of
the
portfolio insensitive
to
small changes
in
the
price of
the
underlying asset. Since
aIT
av
as
=
as
-
~
= 0,
it
follows
that
the
value
of
the
portfolio over
the
small
time
period
dt corre-
sponding
to
the
change
in
the
price
of
the
underlying asset from S
to
S + dS
3If
the
underlying asset
paid
dividends continuously
at
the
rate
q)
then
dll
=
dV
-
!::"dS
-
q!::"Sdt.

160
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
is fully deterministic. To avoid
arbitrage
opportunities,
the
value
of
this
portfolio
must
grow
at
the
same
rate
as
the
risk free interest
rate
r, i.e.,
dIl
=
rIl
dt. (5.64)
From
(5.63)
and
(5.64), we conclude
that
0-
2
8
2
rIl
~
8 +
--r.
2
(5.65)
We
note
that
the
approximate
formula (5.65) is
actually
an
equality for
plain
vanilla
European
options;
d.
(6.53) for q =
O.
This
equality
can
be
derived
using
the
Black-Scholes
PDE;
see section 6.4.2 for details.
5.5
Approximation
of
the
Black-Scholes
formula
for
at-the-money
options
For
at-the-money
options,
approximations
to
the
Black-Scholes formula
that
do
not
require
estimating
the
cumulative density function
of
the
standard
normal
distributions
can
be
derived.
These
formulas
are
easy
to
compute
and,
in
many
cases, very accurate.
In
section 5.5.1, we present several such approximations formulas, in-
cluding approximations for
the
Greeks
and
for
the
implied volatility.
These
formulas
are
proved
in
section 5.5.2.
In
section 5.5.3, we derive a
theoretical
bound
for
the
precision
of
the
approximation
of
the
price for ATM
options
on
non-dividend-paying
assets for
the
case
of
zero interest rates.
We
also
investigate
the
relative
approximation
error
of
the
formulas from section 5.5.1
for two
particular
examples.
5.5.1
Several
ATM
approximations
formulas
The
most
commonly used
approximation
formulas
are
for
at-the-money
op-
tions
on
assets paying no dividends,
with
zero risk-free rates:
I r =
0;
q =
0:
p = C
""
aBjf"
""
0.4
as,fT
I
For
the
general case when
rand
q
are
nonzero,
the
following
approximation
formulas
can
be
used for pricing ATM
plain
vanilla
European
options:
r
-#
0;
q
-#
0:
r
-#
0;
q
-#
0:
C
~
0-8jf"
(1-
(r+
2
q
)T)
+
(r-
2
q
)T
8
(r-q)T
8
2
5.5.
BLACK-SCHOLES
FORMULA:
ATM
APPROXIMATIONS
161
Approximation
formulas
can
also
be
obtained
for
the
implied volatility
of
ATM options:
r = q =
0:
o-imp
r
-#
0;
q
-#
0:
o-imp
If
r = q = 0,
the
following
approximation
formulas
can
be
used for
the
Greeks
of
ATM
options
(similar,
but
more
complicated formulas exist for
r,
q
-#
0):
Ll(C)
~
~
+
;flir
~
~
+ 0.20-VT
Ll(P)
r(c)
=
r(p)
~
_1_
(1-
(J"2T)
~
(J"S~
8
0.4
(J"s.,fT
vega(C)
=
vega(P)
~
8jf"
(1
_
(J"~T)
~
0.48VT
(1
_
(J"?)
8(C)
=
8(P)
~
- 2:;f;r
(1
-
(J"~T)
~
0.2(J"S
(1
_
(J"28
T
)
-.,fT
p(C)
~
8T
(~-
;flir)
~
8T
(~-
0.20-
VT
)
p(P)
8T
(~+
0.20-
VT
)
5.5.2
Deriving
the
ATM
approximations
formulas
We begin
by
proving
that,
if r = 0
and
q = 0,
the
prices
of
the
ATM call
and
ATM
put
are
equal,
and
can
be
approximated
as
P = C
~
0-8
ff
V2;'
or,
in
a simpler
to
compute
but
less precise way, as
. 1
smce
V2ir
P = C
~
0.4
0-8Vr,
0.39894228
~
0.4.
(5.66)
(5.67)
162
CHAPTER
5.
TAYLOR'S
FORMULA.
TAYLOR
SERIES.
Since r = q = 0
and
K =
S,
it
is easy
to
see from
the
Put-Call
parity
(1.47)
that
the
values of
the
put
option
and
call options are
the
same:
P =
Ke-
rT
S+C =
S-S+C
= C.
(5.68)
For
an
ATM call
and
assuming zero interest
rates
and
a non-dividend-
paying asset, i.e., for
K =
S,
r = 0,
and
q = 0,
the
Black-Scholes formula
(3.53) corresponding
to
t = 0
can
be
written
as
(
CYVT)
(
CYVT)
C =
SN
-2-
-
SN
--2-
.
(5.69)
From
(3.43), we find
that
N (
_o-f)
= 1 - N
(o-f)
and
(5.69) becomes
(5.70)
We
approximate
the
term
N
(o-f)
using a Taylor approximation
around
o.
From
(5.7) for f(x) = N(x), a = 0,
and
n =
2,
we
obtain
that
2
N(x) =
N(O)
+ xN'(O) +
~
N"(O)
+ O(x
3
),
(5.71)
as
x
---+
o.
Recall
that
N(t) =
.~
jt
e-~
dy.
V
27f
-00
It
is easy
to
see
that
N(O)
=
~;
cf. (3.43) for a =
O.
From
Lemma
2.3,
~
1
-~
we
obtain
that
N'(t) =
vke-T,
and
therefore N"(t) = -
y'2ifte
2.
Thus,
N(O)
=
~,
N'(O)
=
vk,
N"(O)
=
0,
and
the
Taylor expansion (5.71) of
N(x)
around
the
point 0 becomes
4
1 x 3 1 x
N(x) = - +
fCC
+ O(x )
~
-2
+
fCC·
(5.72)
2 v27f v27f
---------------------
4We
note
that
the
Taylor expansion (5.72)
can
be
more accurately
written
as
1 x x
3
1 5
N(x) = - + .
/"iC
- - .
/"iC
+
O(x),
as x
-t
0,
2 y27r 6 Y
27r
since NII/(O) = -
vk,
N(4)(0) =
0,
and
N(5)(0) = k
=f
o.
This
level of precision is
not
needed here.
5.5.
BLACK-SCHOLES
FORMULA:
ATM
APPROXIMATIONS
163
Thus,
N
(CYVT)
~
~
+
_1_
cyVT
2 2
Viii
2'
(5.73)
and, by
substituting
(5.73) into (5.70), we find
that
which is
the
same
as (5.66).
By
solving (5.66) for
CY,
we
obtain
the
following
estimate
for
the
implied
volatility
of
an
ATM
call option:
C 2.5 C
CYimp
~
y'2;
SVT
~
SVT;
(5.74)
see sections 3.6.2
and
8.6 for more details
on
implied volatility.
Formula (5.66) is a good approximation for
the
Black-Scholes value of
ATM options only if
the
Taylor approximation (5.72) is accurate.
In
sec-
tion
5.5.3, we show
that,
for options
with
maturities
less
than
one year
and
volatility slightly smaller
than
50%,
the
approximation
given by (5.66) is
within
one
percent
of
the
Black-Scholes
option
price; see
Theorem
5.7 for
the
precise result.
The
following approximations of
the
Black-Scholes formulas for
at-the-
money options if r
i=
0
and
q
i=
0, i.e.,
c
""
aBjl;
(1
(r
+2
q)T)
p
"'"
usjl;
(1
-
(r
+2
q)T)
+
(r
-
q)T
S.
2 '
(r
q)T
S
2 '
(5.75)
(5.76)
can
be
obtained
similarly. We only derive (5.75) here. For
an
ATM call
option,
the
Black-Scholes formula (3.53) corresponding
to
t = 0 becomes
From
the
Taylor expansion (5.72) for N(x), i.e., N(x)
~
~+
V&'
we find
that
- e
-+
+--
C
-
S
-qT
(1
(r
-
q)VT
CYVT)
2
cyViii
2
Viii
