Stefanica D. A Primer for the Mathematics of Financial Engineering
Подождите немного. Документ загружается.

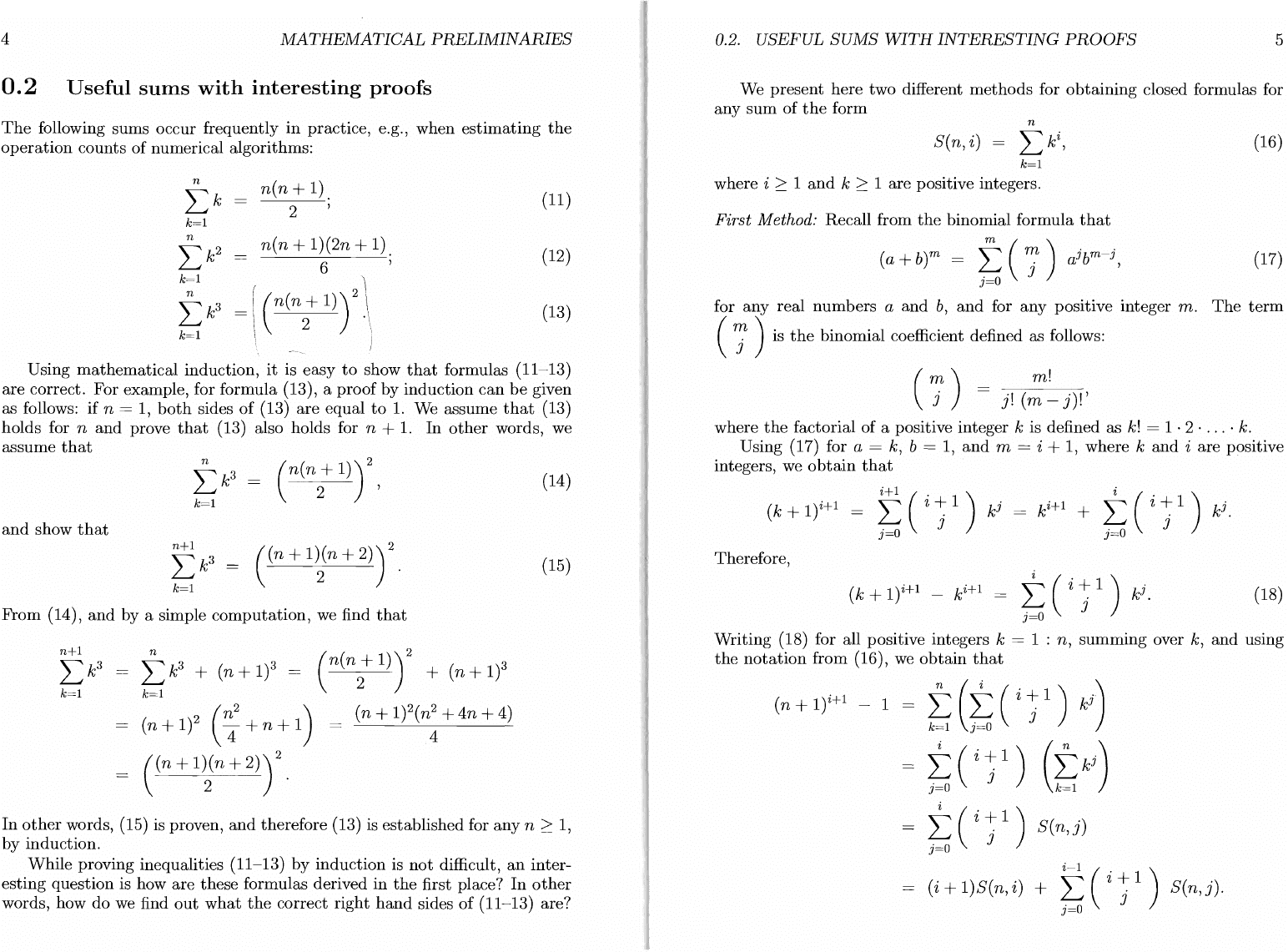
4
MATHEMATICAL
PRELIMINARIES
0.2
Useful
sums
with
interesting
proofs
The
following
sums
occur
frequently
in
practice,
e.g.,
when
estimating
the
operation
counts
of
numerical
algorithms:
n
n(n
+ 1).
Lk
(11)
2
,
k=l
n
n(n
+ 1)(2n + 1).
Lk
2
(12)
6
,
k=l
n
(n(n
2
+
1)),
Lk
3
(13)
k=l
Using
mathematical
induction,
it
is
easy
to
show
that
formulas (11-13)
are
correct.
For
example, for
formula
(13), a
proof
by
induction
can
be
given
as
follows:
if
n =
1,
both
sides
of
(13)
are
equal
to
1.
We
assume
that
(13)
holds
for n
and
prove
that
(13) also holds for n + 1.
In
other
words, we
assume
that
(14)
and
show
that
I:k
3
=
en
+
1)2(n
+
2)),
k=l
(15)
From
(14),
and
by
a simple
computation,
we find
that
In
other
words, (15) is proven,
and
therefore
(13) is
established
for
any
n
~
1,
by
induction.
While
proving
inequalities (11-13)
by
induction
is
not
difficult,
an
inter-
esting
question
is how
are
these
formulas derived
in
the
first place?
In
other
words,
how
do
we find
out
what
the
correct
right
hand
sides
of
(11-13)
are?
0.2. USEFUL
SUMS
WITH
INTERESTING
PROOFS
5
We
present
here
two
different
methods
for
obtaining
closed formulas for
any
sum
of
the
form
n
S(n, i) = L k
i
,
k=l
where
i
~
1
and
k
~
1
are
positive integers.
First Method:
Recall
from
the
binomial
formula
that
(a +
b)m
= f (
rr:)
ajb
m
-
j
,
j=O
J
(16)
(17)
for
any
real
numbers
a
and
b,
and
for
any
positive
integer
m.
The
term
( 7 ) is
the
binomial coefficient defined
as
follows:
(7)
-
j!
(::~j)!'
where
the
factorial
of
a positive integer k is defined
as
k!
= 1
·2·
....
k.
Using (17) for a =
k,
b =
1,
and
m = i +
1,
where
k
and
i
are
positive
integers, we
obtain
that
(k
+ 1)i+l = f ( i
~
1)
k
j
= ki+l + t ( i
~
1)
k
j
.
j=O
J
j=O
J
Therefore,
(k
+ 1)i+l - ki+l = t ( i
~
1)
k
j
.
j=O
J
(18)
Writing
(18) for all positive integers k = 1 : n,
summing
over
k,
and
using
the
notation
from
(16), we
obtain
that

6
MATHEMATICAL
PRELIMINARIES
We established
the
following recursive formula for S
(n,
i) =
2:~=1
ki:
S(n,
i) =
-.
- (n +
l)i+I
- 1 - L
~
~
S(n,j)
,
1 (
i-I
(.
1)
)
~
+ 1
j=O
J
(19)
for all
i
~
1.
It
is easy
to
see
that,
for i = 0,
n n
S(n,O) = L
ko
=
Ll
= n.
k=l
k=l
Example: Use
the
recursion formula (19)
to
compute
S(n,
1) =
2:~=1
k
and
S(n,
2) =
2:~=1
k
2
.
Answer: Recall
that
S(n,
0) = n. For i = 1, formula (19) becomes
1
S(n,
1)
=
2"
((n
+
1)2
-1
- 0)
s(n,o))
1
2"
((n+l?-I-n)
n(n +
1)
2
which is
the
same as formula
(11).
For
i = 2, formula (19) becomes
S(n,
2)
=
~
((n+1)3-1
1
3
((n+l)3-1
~
((n+1)3-
1
1 2n
3
+ 3n
2
+ n
3 2
which is
the
same as formula (12). 0
~
(
~)
s(n,j))
S(n,O) -
3S(n,
l) )
n _ 3n(n
2
+1))
n(n
+ 1)(2n +
1)
6
Second Method:
Another
method
to
compute
S(n,
i)
=
2:~=1
k
i
,
for i
~
°
positive integer is
to
find a closed formula for
n
T(
. ) -
~kj
k
n,J,x
- 6
x,
k=l
where j
~
° is
an
integer
and
x E
JR,
and
then
evaluate
T(n,j,
x)
at
x = 1
to
obtain
n
S(n,
i)
T(n,
i,
1)
L
ki,
\;j
n
~
1,
i
~
1.
(20)
k=l
0.2. USEFUL
SUMS
WITH
INTERESTING
PROOFS
We provide a recursive formula for evaluating
T(n,j,x£.
For j = 0, we find
that
T(n,
0,
x) =
2:~=1
xk =
2:~=o
x
~
k
1-
x
n
+
I
6
x
=
I-x'
k=O
which
can
be
seen, e.g., by cross multiplication,
it
follows
that
T(n,O,x)
Note
that
n
1-
xn+I
I-x
n
L (xk - x
k
+
I
)
k=O
- 1,
\;j
n
~
1, x E
JR.
7
1.
Since
(21)
(22)
x
d~
(T(n,j,
x))
X
Lk
j
.
kx
k
-
I
k=l
T(n,j+l,x).
Thus,
the
following recursion formula holds:
T(n,j+l,x)
=
x~(T(n,j,x)),
\;jj~O.
dx
(23)
Formulas (22)
and
(23) can be used
to
evaluate
T(n,j,
x)
at
any point x E
JR,
and
for
any
integers n
~
1
and
j
~
0.
We
note
that
evaluating
T(n,
i,
x)
at
x =
1,
which is needed
to
compute
S(n,
i), see (20), requires using l'Hopital's rule
to
compute
limits as x
---t
1.
Example: Use
the
recursion formula (23)
and
the
fact
that
S(n,
i) =
T(n,
i,
1)
for
any
positive integer i
to
compute
S
(n,
1) =
2:~=1
k.
Answer:
For j = 0, formula (23) becomes
T(n,
1,
x)
Using (22),
it
follows
that
T(n,
1,
x)
d
x dx
(T(n,
0, x)).
x - (n
+ l)xn+I +
nx
n
+
2
(1
-
x)2
(24)
Then,
the
value
of
S(n,
1) =
T(n,
1,
1)
can
be
obtained
by
computing
the
limit of
the
right
hand
side of (24) as x
---t
1.
Using l'Hopital's rule, see

8
MATHEMATICAL
PRELIMINARIES
Theorem
1.8, we
obtain
that
. x -
(n
+
l)xn+l
+
nx
n
+
2
S(n, 1) = T(n, 1, 1) =
hm
------'-------:---'-------:-::c---
x-)l
(1-
X)2
.
1-
(n
+
l)2xn
+
n(n
+ 2)xn+l
hm
-------=-----:----':----'---
x-)l
-2(1
-
x)
.
-n(n
+ 1)2
x
n-l
+
n(n
+
l)(n
+
2)xn
hm
2
x-)l
-n(n
+
1)2
+
n(n
+
l)(n
+ 2)
n(n
+ 1)
2 2
which is
the
same
as formula (11). 0
0.3
Sequences
satisfying
linear
recursions
Definition
0.3.
A sequence
(xn)n~O
satisfies a linear recursion
of
order k
if
and
only
if
there exist
constants
ai, i = ° :
k,
with
ak # 0,
such
that
k
LaiXn+i
= 0, V n
~
0.
(25)
i=O
The
recursion (25) is called a linear recursion because
of
the
following
linearity
properties:
(i)
If
the
sequence (xn
)n~O
satisfies
the
linear
recursion (25),
then
the
sequence
(zn)n~O
given
by
Zn
=
Cx
n
,
V n
~
0,
(26)
where C is
an
arbitrary
constant,
also satisfies
the
linear recursion (25).
(ii)
If
the
sequences
(xn)n~O
and
(Yn)n~O
satisfy
the
linear recursion (25),
then
the
sequence
(zn)n~O
given
by
Zn
=
Xn
+
Yn,
V n
~
0,
(27)
also satisfies
the
linear recursion (25).
Note
that,
if
the
first k
numbers
of
the
sequence, i.e., xo, Xl,
...
,
Xk-l,
are
specified,
then
all entries
of
the
sequence
are
uniquely
determined
by
the
recursion formula (25): since ak # 0, we
can
solve (25) for
Xn+k,
i.e.,
1
k-l
LaiXn+i
V n
~
0.
ak
i=O
(28)
0.3.
SEQUENCES
SATISFYING
LINEAR
RECURSIONS
9
If
Xo,
Xl,
...
,
Xk-l
are
given, we find
Xk
by
letting
n = °
in
(28).
Then
Xl,
X2,
...
,
Xk
are
known
and
we find
Xk+l
by
letting
n = 1
in
(28),
and
so on.
In
Theorem
0.1, we will present
the
general formula
of
Xn
in
terms
of
Xo,
Xl,
...
,
Xk-l'
To do so, we first define
the
characteristic polynomial
2
associated
to
a
linear
recursion.
Definition
0.4.
The characteristic
polynomial
P(z)
corresponding to
the
lin-
ear recursion
2::=0
aiXn+i = 0,
for
all n
~
0,
is
defined as
k
P(z)
= L
aiz
i
.
i=O
(29)
Note
that
P(z)
is a polynomial
of
degree
k,
i.e.,
deg(P(z))
=
k.
Recall
that
every polynomial
of
degree k
with
real coefficients
has
exactly k
roots
(which could
be
complex numbers), when
counted
with
their
multiplicities.
More precisely,
if
P(z)
has
p different
roots
Aj, j = 1 : p,
with
p
::;
k,
and
if
m(Aj)
denotes
the
multiplicity of
the
root
Aj,
then
2:~=l
m(Aj)
= k.
Theorem
0.1.
Let
(xn)n~O
be
a sequence
satisfying
the linear recursion
k
LaiXn+i
=
0,
V n
~
0,
i=O
(30)
with ak # 0,
and
let
P(z)
=
2::==-~
aizi
be
the characteristic polynomial asso-
ciated to recursion
(30).
Let
Aj, j = 1 :
p,
where p ::; k,
be
the roots
of
P(z),
and
let
m(
Aj)
be
the
multiplicity
of
Aj.
The
general
form
of
the sequence
(xn)n~O
satisfying
the linear recursion (30) is
Xl,
Vn~O,
(31)
where Ci,j are
constant
numbers.
Example:
Find
the
general formula for
the
terms
of
the
Fibonacci sequence
1,
1,
2,
3,
5, 8, 13, 21,
...
,
where each new
term
is
the
sum
of
the
previous two
terms
in
the
sequence.
2The
same
characteristic polynomial corresponds
to
the
linear
ODE
with
constant
coef-
ficients
I:~=o
aiy(i)
(x) =
O.

10
MATHEMATICAL
PRELIMINARIES
Answer:
By
definition,
the
terms
of
the
Fibonacci sequence satisfy
the
linear
recursion
Xn+2
=
Xn+1
+ X
n
, for all n
~
0,
with
Xo
=
1,
and
Xl
=
1.
This
recursion
can
be
written
in
the
form (25) as
Xn+2
-
Xn+1
-
Xn
=
0,
V n
~
O.
The
characteristic polynomial associated
to
the
linear recursion (32) is
P(z)
=
Z2
- Z - 1,
and
the
roots of
P(z)
are
A1
= 1 +
VS
and
A2
2
From
Theorem
0.1, we find
that
I-VS
2
Xn
=
C1A~
+
C2A~,
V n
~
0,
(32)
(33)
(34)
where
A1
and
A2
are given by (33).
The
constants
C
1
and
C
2
are
chosen
in
such a way
that
Xo
= 1
and
Xl
=
1,
i.e., such
that
{
C1
+ C
2
1;
C1A1
+
C2A2
=
1.
The
solution
to
this linear
system
is
C _ VS+l
1 -
2VS
and
We conclude from (34)
that
the
general formula for
(xn)n~O
is
Xn
=
VS
+ 1
(1
+
vs)
n +
VS
- 1
(1
_
vs)
n
2VS
2
2VS
2
~
(1
+
vs)n+1
__
1
(1-
VS)n+1 V n
~
O.
VS
2
VS
2
o
A complete proof of
Theorem
0.1 is technical
and
beyond
the
scope
of
this
book. For
better
understanding, we provide more details for
the
case when
the
polynomial
P(z)
has
k different roots,
denoted
by
Al,
A2,
...
Ak.
We
want
to
show
that,
if
the
sequence
(xn)n~O
satisfies
the
recursion
k
LaiXn+i
=
0,
V n
~
0,
i=O
(35)
0.3.
SEQUENCES
SATISFYING
LINEAR
RECURSIONS
then
there
exist constants C
j
,
j = 1 : k, such
that
k
11
Xn
= L CjX] , V n
~
0,
(36)
j=l
which is
what
the
general formula (31) reduces
to
in
this
case.
If
Aj
is a
root
of
P(z),
then
P(Aj) =
L~=o
ai
A~
=
O.
It
is easy
to
see
that
the
sequence
Yn
= CXj, n
~
0, where C is
an
arbitrary
constant, satisfies
the
linear recursion (25):
k k k
LaiYn+i
=
Lai
CX]+i
= CX]
Lai
A;
= CX] P(Aj) =
O.
i=O i=O i=O
Using
the
properties (26)
and
(27),
it
follows
that
the
sequence
(Zn)n~O
given by
k
Zn
= L CjAj, V n
~
0,
(37)
j=l
satisfies
the
linear recursion (35), where Cj, j = 1 :
k,
are
arbitrary
constants.
Let
(xn)n~O
satisfying recursion (35),
and
let
Xo,
Xl,
...
,
Xk-1
be
the
first
k numbers
of
the
sequence.
If
we can find
constants
Cj, j = 1 :
k,
such
that
the
first k
numbers
in
the
sequence
(xn)n~O
and
in
the
sequence
(zn)n~O
given
by (37) are equal,
then
it
is easy
to
see, e.g., by complete induction,
that
Xn
=
Zn,
for all n
~
0, i.e.,
that
the
two sequences are identical, which is
what
we
want
to
show.
We are looking for constants
(C
j
)j=l:k,
such
that
k
Xi
=
zi
=
LCjA~,
Vi=O:(k-l).
j=l
In
other
words, Cj, j = 1 :
k,
must
solve
the
linear
system
k
LCjA;
=
Xi,
Vi=O:(k-'-I),
j=l
which
can
be
written
in
matrix
form as
AC
=
b,
where A is
the
k x k
matrix
given by
1 1
A
(38)
(39)

12
MATHEMATICAL
PRELIMINARIES
and
0
and
b denote
the
k x 1 row vectors
The
matrix
A is called a
Vandermonde
matrix.
It
can
be
shown
(but
is
not
straightforward
to
prove)
that
det(A)
IT
(Aj - Ai).
1~i<j~k
Since we assumed
that
the
roots
A1,
A2,
...
Ak
of
the
characteristic polynomial
P(z)
are
all different, we conclude
that
det(A)
oF
O.
Therefore
the
matrix
A
is nonsingular
and
the
linear
system
(39)
has
a unique solution.
Then,
if
(OJ)
j=1:k
represents
the
unique
solution of
the
linear
system
(39),
the
sequence
(xn)n~O
given
by
Xn
=
2:;=1
OjX], for n
~
0, is
the
only sequence
satisfying
the
linear recursion
(35)
and
having
the
first k
terms
equal
to
Xo,
Xl,
...
,
Xk-1'
0.4
The
"Big
0"
and
"little
0"
notations
The
need for
the
"Big
0"
notation
becomes clear when looking
at
the
behavior
of
a polynomial
P(x)
when
the
argument
x is large.
Let
n
P(x)
=
L:
ak
xk
,
k=O
with
an
oF
O.
It
is easy
to
see
that,
as x
-7
00,
the
term
of
largest degree, i.e.,
anx
n
,
dominates
all
the
other
terms:
1
·
IP(x)1 _ l'
12:~=Oakxkl
_ l' +
L:
n
-
1
ak
Im---
1m
-
1m
an
--
x--+oo xn x--+oo xn x--+oo x
n
-
k
k=O
The
"Big
0"
notation
is used
to
write
the
information contained
in
(40)
in
a
simplified way
that
is well
suited
to
computations,
i.e.,
P(x)
=
O(xn),
as
x
-7
00.
Formally,
the
following definition
can
be
given:
0.4.
THE
"BIG
0"
AND
"LITTLE
0"
NOTATIONS
13
Definition
0.5.
Let
f,g
:
JR
-7
JR.
We write
that
f(x)
O(g(x)),
as
x
-7
00,
if
and only
if
("iff") there exist constants 0 > 0 and M > 0 such
that
I
~~:j
I
~
0,
for
any
x
~
M.
This can
be
written
equivalently
as
f(x)
=
O(g(x)),
as
x
-7
00,
iff
lim
sup
I
f((X))
I <
00.
x--+oo g X
(41)
The
"Big
0"
notation
can
also
be
used for x
-7
-00,
as
well as for x
-7
a:
f(x)
=
O(g(x)),
as
x-7-oo,
iff
lim
sup
I
f((
x))
I <
00;
x--+-oo
g X
(42)
f(x)
=
O(g(x)),
as x
-7
a,
iff
lim
sup
I
f((X))
I <
00.
x--+a g X
(43)
We
note
that
the
estimate
(43)
is
most
often
used for a =
0,
i.e., for x
-7
O.
The
"little
0"
notation
refers
to
functions whose
ratios
tend
to
0
at
certain
points,
and
can
be
defined for x
-7
00,
X
-7
a,
and
x
-7
-00
as follows:
Definition
0.6.
Let
f,
g :
JR
-7
JR.
Then,
f(x)
o(g(x)),
as
x
-7
00,
iff
lim I f(x) I
=
O'
(44)
x--+oo
g(x)
)
f(x)
o(g(x)),
as
x
-7
-00,
iff
r
If(x)1
x-2~oo
g(x)
O'
,
(45)
f(x)
o(g(x)),
as
x
-7
a,
iff
r
If(x)1
x~
g(x)
=
O.
(46)
The
rules for
operations
with
0(·)
and
0('), e.g., for additions,
subtrac-
tions, multiplications follow from
the
definitions (41)-(46).
Example:
If
0 < n <
m,
then
o(xm),
O(x
m
),
o(xn),
O(x
n
),
as x
-7
00;
as x
-7
00;
as x
-7
0;
as x
-7
O.
Answer: We only sketch
the
proofs
of
(47-49).
To prove
(47),
note
that,
since m >
n,
I
xn I 1
lim - =
lim--
x--+oo xm
x-too
x
m
-
n
O.
(47)
(48)
(49)
(50)

14
MATHEMATICAL
PRELIMINARIES
Therefore,
xn
= o(xm), as x
~
00;
d.
definition (44).
To prove
(49),
we
obtain
similarly
that
lim Ixml = lim
JxJm-n
= 0,
x---tQ
xn
x---tQ
and
therefore
xm
= o(xn), as x
~
0;
cf. definition (46).
To prove
(48),
i.e.,
that
O(xn)+O(xm) = O(x
m
),
as x
~
00,
ifO < n <
m,
let
f,g
:
IR
~
IR
such
that
f(x) = O(xn), as x
~
00,
and
g(x) = O(xm), as
x
~
00.
By
definition (41),
it
follows
that
limsuplf(~)1
<
00
and
lim
sup
Ig(:)
I <
00.
~oo
X
~oo
X
In
other
words,
there
exist
constants
OJ, M
j
and
Og,
M
g
, such
that
If;~)
I
:S
Of,
It
x
'2
M
f
and
Ig;~)
I
:S
Og,
It
x
'2
Mg.
(51)
Let
h(x) = f(x) + g(x). To show
that
h(x) = O(xm), as x
~
00,
it
is
enough
to
prove
that
there
exist
constants
Oh
and
Mh such
that
Ih;~)
I
:S
Oh,
It
x
'2
M
h
.
(52)
From
(51),
it
follows
that,
for
any
x
2::
max(Mj,
Mg),
I
h(x)1 = If(X)+g(x)1
~
If(x)1 +
Ig(X)1
~
_1
0
xm
xm
xm
xm
x
m
-
n
j
+
Og.
(53)
Note
that
limx---too
x
2
-
n
=
0,
since m >
n.
From
(53),
it
follows
that
we
can
find
constants
Oh
and
Mh such
that
(52)
holds
true,
and
therefore
(48)
is
proved. D
Similarly,
it
can
be
shown
that,
for
any
n > 0,
O(xn) + O(xn) = O(xn); O(xn) - O(xn) = O(xn);
o(x
n
)
+ o(x
n
) = o(xn); o(xn) - o(xn) = o(xn).
Finally,
note
that,
by definition,
-O(g(x))
= O(g(x)), and, similarly,
-o(g(
x)) =
o(g(
x)). More generally, for any
constant
c
=F
0, we
can
write
that
O(cg(x)) = O(g(x))
and
c O(g(x)) = O(g(x));
o(cg(x))
= o(g(x))
and
c o(g(x)) = o(g(x)).
The
0(·)
and
0(')
notations
are
useful for Taylor approximations as well
as for finite difference approximations; see, sections 5.1
and
6.1 for details.
0.5.
EXERCISES
15
0.5
Exercises
1.
Let f :
IR
~
IR
be
an
odd
function.
(i) Show
that
xf(x)
is
an
even function
and
x
2
f(x)
is
an
odd
function.
(ii) Show
that
the
function
gl
:
IR
~
IR
given
by
gl
( x) = f
(x
2
)
is
an
even function
and
that
the
function
g2
:
IR
~
IR
given by
g2(X)
=
f(x
3
)
is
an
odd
function.
(iii)
Let
h :
IR
~
IR
be
defined as h(x) = xi
f(x
j
),
where i
and
j are
positive integers.
When
is
h(
x)
an
odd
function?
2. Let S(n, 2) =
I:~=1
k
2
and
S(n, 3) =
I:~=1
k
3
.
(i) Let
T(n,2,x)
=
I:~=1
k
2
xk.
Use formula
(23)
for j =
1,
i.e.,
d
T(n, 2, x) = x dx (T(n, 1, x)),
and
formula
(24)
for T(n,
1,
x),
to
show
that
x + x
2
-
(n
+
1?xn+1
+
(2n2
+ 2n -
1)xn+2
- n
2
x
n
+
3
T(n,2,x)
=
(1-x)3
(ii) Note
that
S(n,2) = T(n,
2,1).
Use
l'Hopital's
rule
to
evaluate
T(n
2
1)
and
conclude
that
S(n
2) =
n(n+1)(2n+1)
, , , ,
6'
(iii)
Compute
T(n,
3,
x) =
I:~=1
k
3
xk
using formula
(23)
for j =
2,
i.e,
d
T(n,3,x)
= x
dx(T(n,2,x)).
(iv) Note
that
S(n,3) = T(n, 3,1). Use
l'Hopital's
rule
to
evaluate
T(n,3, 1),
and
conclude
that
S(n,3) = (n(n;1))
2.
3.
Compute
S(n,4) =
I:~=1
k4
using
the
recursion formula (19) for i = 4,
the
fact
that
S(n,
0)
= n,
and
formulas (11-13) for S(n, 1), S(n, 2),
and
S(n,3).
4.
It
is easy
to
see
that
the
sequence
(X
n
)n;:::l
given by
Xn
satisfies
the
recursion
(54)

16
MATHEMATICAL
PRELIMINARIES
with
Xl
=
1.
(i)
By
substituting
n + 1 for n
in
(54),
obtain
that
Xn+2
=
Xn+l
+ (n +
2?
(55)
Subtract
(54) from (55)
to
find
that
X
n
+2
=
2Xn+l
-
Xn
+
2n
+ 3, V n
;::::
1,
(56)
with
Xl
= 1
and
X2
=
5.
(ii) Similarly,
substitute
n + 1 for n in (56)
and
obtain
that
X
n
+3
=
2Xn+2
-
Xn+l
+
2(n
+ 1) + 3.
(57)
Subtract
(56) from (57)
to
find
that
X
n
+3
=
3X
n
+2
-
3X
n
+l
+
Xn
+
2,
V n
;::::
1,
with
Xl
=
1,
X2
=
5,
and
X3
= 14.
(iii) Use a similar
method
to
prove
that
the
sequence
(xn)n~O
satisfies
the
linear recursion
Xn+4
-
4X
n
+3
+
6X
n
+2
-
4Xn+l
+
Xn
=
0,
V n
;::::
1.
The
characteristic polynomial associated
to
the
recursion (58) is
P(z)
=
z4
-
4z
3
+
6z
2
-
4z
+ 1 = (z - 1)4.
(58)
Use
the
fact
that
Xl
=
1,
X2
= 5,
X3
= 14,
and
X4
= 30
to
show
that
n(n
+ 1)(2n +
1)
\-I
6 ' v
n;::::
1,
and
conclude
that
n
S(n,2)
= Lk
2
k=l
n(n
+ 1)(2n +
1)
6
Vn;::::1.
5.
Find
the
general form of
the
sequence
(xn)n~O
satisfying
the
linear re-
cursion
X
n
+3
=
2Xn+l
+ X
n
, V n
;::::
0,
with
Xo
=
1,
Xl
=
-1,
and
X2
=
1.
0.5.
EXERCISES
6.
The
sequence
(xn)n~O
satisfies
the
recursion
Xn+l
=
3x
n
+
2,
V n
;::::
0,
with
Xo
=
1.
(i) Show
that
the
sequence
(xn)n~O
satisfies
the
linear recursion
X
n
+2
=
4Xn+l
-
3x
n
,
V n
;::::
0,
with
Xo
= 1
and
Xl
=
5.
(ii)
Find
the
general formula for X
n
,
n;::::
0.
7.
The
sequence
(xn)n~O
satisfies
the
recursion
Xn+l
=
3x
n
+ n +
2,
V n
;::::
0,
with
Xo
=
1.
(i) Show
that
the
sequence
(xn)n~O
satisfies
the
linear recursion
X
n
+3
=
5X
n
+2
-
7Xn+l
+
3x
n
,
V n
;::::
0,
with
Xo
=
1,
Xl
=
5,
and
X2
= 18.
(ii)
Find
the
general formula for X
n
,
n
;::::
0.
17
8.
Let
P(z)
=
2:7=0
aizi
be
the
characteristic polynomial corresponding
to
the
linear recursion
k
LaiXn+i
=
0,
V
n;::::
0.
i=O
(59)
Assume
that
A is a root of multiplicity 2 of
P(z).
Show
that
the
se-
quence
(Yn)n~O
given
by
Yn
=
CnA
n ,
n;::::
0,
where C is
an
arbitrary
constant, satisfies
the
recursion (59).
Hint: Show
that
k
L
aiYn+i
=
CnA
n
P(A)
+ CA
n
+
l
P'(A), V
n;::::
0,
i=O
and
recall
that
A is a root of multiplicity 2 of
the
polynomial
P(
z)
if
and
only if P(A) = °
and
P'(A) =
0.

18
MATHEMATICAL
PRELIMINARIES
9.
Let
n >
O.
Show
that
O(xn) + O(xn)
o(xn)
+ o(x
n
)
as x
----+
0;
as x
----+
O.
(60)
(61)
For example,
to
prove
(60),
let
f(x)
= O(xn)
and
g(x) = O(xn) as
x
----+
0,
and
show
that
f(x) + g(x) = O(xn) as x
----+
0, i.e.,
that
1
.
If(X)+g(x)1 <
1m
sup
00.
x--+o
Xn
10.
Prove
that
k=l
i.e., show
that
L:
n
k
2
lim
sup
k=; <
00
n--+oo
n
and
that
~n
k
2
_
n
3
1
·
6k=1
3
1m
sup
2 <
00.
n--+oo
n
Similarly, prove
that
n
k=l
n
Chapter
1
Calculus
review.
Plain
vanilla
options.
Brief review
of
differentiation:
Product
Rule,
Quotient
Rule,
Chain
Rule for
functions
of
one
variable. Derivative of
the
inverse function.
Brief review
of
integration:
Fundamental
Theorem
of
Calculus,
integration
by
parts,
integration
by
substitution.
Differentiating definite integrals
with
respect
to
parameters
in
the
limits
of
integration
and
with
respect
to
parameters
in
the
integrated
function.
Limits.
L'Hopital's
Rule. Connections
to
Taylor expansions.
Multivariable functions.
Partial
derivatives.
Gradient
and
Hessian of multi-
variable functions.
1.1
Brief
review
of
differentiation
We begin
by
briefly reviewing
elementary
differentiation topics for functions
of
one variable.
The
function f :
1R
----+
1R
is differentiable
at
the
point
x E
1R
if
the
limit
1
.
f(x+h)-f(x)
1m-----'----''--------'---'---
h--+O
h
exists,
in
which case
the
derivative
l
f'
(x)
is defined as
f'(x) = lim
f(x
+
h)
f(x)
h--+O
h
(1.1
)
The
function f (x) is called differentiable if
it
is differentiable
at
all points
x.
Theorem
1.1.
(Product
Rule.)
The
product f(x)g(x) of
two
differentiable
functions f (x)
and
g(
x)
is
differentiable,
and
(f(x)g(x))' = f'(X)g(X) + f(x)g'(x).
(1.2)
1 We
anticipate
by
noting
that
the
forward
and
backward finite difference approximations
of
the
first derivative
of
a function
can
be
obtained
from definition (1.1); see (6.3)
and
(6.5).
19

20
CHAPTER
1. CALCULUS
REVIEW.
OPTIONS.
Theorem
1.2.
(Quotient
Rule.)
The quotient
~~~?
of
two differentiable
functions f (x) and g(
x)
is differentiable at every point x where the
function
~~~?
is well defined) and
(
f(X))'
g(x)
f'(x)g(x)
-
f(x)g'(x)
(g(X))2
(1.3)
Theorem
1.3.
(Chain
Rule.)
The composite function
(gof)(x)
=
g(f(x))
of
two differentiable functions
f(x)
and g(x) is differentiable at every
point
x where
g(f(x))
is well defined) and
(g(f(x)))'
=
g'(f(x))
f'(x).
(1.4)
The
Chain
Rule for multivariable functions is presented
in
section 7.1.
The
Chain
Rule formula (1.4)
can
also
be
written
as
dg dg du
dx
du
dx'
where u =
f(x)
is a function of x
and
g = g(u) =
g(f(x)).
Example: Chain Rule is often used for power functions, exponential functions,
and
logarithmic functions:
d~
((f(x)t)
n(f(x))n-l
J'(x);
(1.5)
dd
x
(ef(X))
ef(x)
f'(x);
(1.6)
d
f'(x)
(1.7)
dx
(In
f(x))
f(x)
.
D
The
derivative of
the
inverse of a function is
computed
as follows:
Lemma
1.1.
Let f :
[a,
b]
-7
[c,
d]
be
a differentiable function) and assume
that
f(x)
has an inverse function denoted by
f-l(x))
with
f-
1
:
[c,
d]
-7
[a,
b].
The function
f-l(x)
is differentiable at every point x E
[c,
d]
where
f'(f-l(x))
of-
0 and
(
-1)'
1 ( )
f (x) =
f'(f-l(x))'
1.8
While we do
not
prove here
that
f-
1
(
x)
is differentiable (this
can
be
done,
e.g., by using
the
definition (1.1)
of
the
derivative of a function), we derive
formula (1.8). Recall from (1.4)
that
(g(f(z)))'
=
g'(f(z))
J'(z).
(1.9)
1.2.
BRIEF
REVIEW
OF
INTEGRATION
21
Let g =
f-
1
in
(1.9). Since
g(f(z))
=
f-l(f(z))
=
Z,
it
follows
that
1 =
(f-l)'
(f(z))
.
J'(z).
(1.10)
Let z
=
f-l(x)
in (1.10). Then,
f(z)
=
f(f-l(x))
= x
and
(1.10) becomes
1
=
(f-l)'
(x) .
f'(f-l(x))
=
(f-l(x))'.
f'(f-l(x)).
(1.11)
If
f'(f-l(x))
of-
0, formula (1.8) follows
immediately
from (1.11).
Examples:
d (
3X2-1)
-
xe
dx
d (
v'3x
2
-
1 )
dx
v'3x
2
-
1 + 4
v'3x
2
-
1
(v'3x
2
-
1 +
4)2
(2x2 -
2x
- 1) e
x2
- 1 .
(x-l)2
,
d
dx
(In(x)
-In(2x2
+
1))
1.2
Brief
review
of
integration
_2X2 + 1
D
X(2x2 +
1)"
In
this
section, we briefly review several
elementary
integration
topics,
both
for antiderivatives
and
for definite integrals.
Let
f :
~
-7
~
be
an
integrable function
2
.
Recall
that
F(
x)
is
the
antiderivative of
f(x)
if
and
only if
F'(x)
=
f(x),
i.e.,
F(x)
~
J
f(x)
dx
~
F'(x)
~
f(x).
(1.12)
The
Fundamental
Theorem
of Calculus provides a formula for evaluat-
ing
the
definite integral of a continuous function, if a closed formula for
its
antiderivative is known.
2Throughout
the
book, by integrable function
we
mean
Riemann
integrable.

22
CHAPTER
1. CALCULUS
REVIEW.
OPTIONS.
Theorem
1.4.
(Fundamental
Theorem
of
Calculus.)
Let
f(x)
be
a
continuous function on the interval
[a,
b],
and let F (x)
be
the antiderivative
of
f(x).
Then
l f(x)
dx
=
F(x)l~
=
F(b)
- F(a).
Integration
by
parts
is
the
counterpart
for integration of
the
product
rule.
Theorem
1.5.
(Integration
by
parts.)
Let
f(x)
and g(x)
be
continuous
functions. Then
j f(x)g(x)
dx
= F(x)g(x) - j F(x)g'(x)
dx,
(1.13)
where
F(x)
= J
f(x)dx
is the antiderivative
of
f(x).
For definite integrals,
l f(x)g(x)
dx
=
F(b)g(b)
- F(a)g(a) - l F(x)g'(x)
dx.
(1.14)
Proof. We apply
the
product
rule (1.2)
to
the
function
F(x)g(x)
and
obtain
(F(x)g(x))'
= (F(x))'g(x) +
F(x)g'(x)
=
f(x)g(x)
+
F(x)g'(x),
(1.15)
since
F'
(
x)
= f (x); cf. (1.12) .
By
taking
antiderivatives
in
(1.15), we con-
clude
that
F(x)g(x) = j f(x)g(x) dx + j F(x)g'(x)
dx,
which is equivalent
to
(1.13).
To derive
the
formula (1.14) for definite integrals, we
apply
the
Funda-
mental
Theorem
of Calculus
to
(1.15)
and
obtain
that
l (f(x)g(x) + F(x)g'(x))
dx
= l (F(x)g(x))'
dx
= (F(x)g(x))
I~
.
This
can
be
written
as
l f(x)g(x)
dx
+ l F(x)g'(x)
dx
which is equivalent
to
(1.14).
F(b)g(b) - F(a)g(a),
o
Integration
by
substitution
is
the
counterpart
for integration
of
the
chain
rule.
1.2.
BRIEF
REVIEW
OF
INTEGRATION
23
Theorem
1.6.
(Integration
by
substitution.)
Let f (x)
be
an integrable
function.
Assume
that
g(
u) is an invertible and continuously differentiable
function. The substitution x
= g( u) changes the integration variable from x
to u
as
follows:
j f(x)
dx
j
f(g(u))g'(u)
duo
(1.16)
For definite integrals,
l
b
19-1(b)
f(x)
dx =
f(g(u))g'(u)
duo
a
g-l(a)
(1.17)
Informally, formula (1.16) follows from
the
fact
that,
by differentiating
the
substitution
formula x = g( u),
it
follows
that
dx
=
g'
(u )du.
The
bounds for
the
definite integrals
in
(1.17) change according
to
the
rule u =
g-l(x).
In
other
words, x = a
and
x = b correspond
to
u =
g-l(a)
and
u = g-l(b),
respectively. Formal proofs of
these
results
are
given below.
Proof. Let
F(x)
= J
f(x)dx
be
the
antiderivative
of
f(x).
The
chain rule
(1.4) applied
to
F(g(
u)) yields
(F(g(u)))' = F'(g(u)) g'(u) =
f(g(u))
g'(u), (1.18)
since
F'
=
f;
cf.
(1.12). Integrating (1.18)
with
respect
to
u, we find
that
j f(g(u))g'(u)
du
=
j(F(g(u)))'
du
= F(g(u)).
(1.19)
Using
the
substitution
x =
g(
u)
we notice
that
F(g(u)) = F(x) = j
f(x)
dx.
(1.20)
From (1.19)
and
(1.20), we conclude
that
j f(x)
dx
= j f(g(u))g'(u)
du
To
obtain
the
formula (1.17) for definite integrals, we
apply
the
Funda-
mental
Theorem
of Calculus
to
(1.18)
and
obtain
1
9
-
1
(b)
f(g(u))g'(u) du
g-l(a)
1
9
-
1
(b)
, g-l(b)
(F(g(u))) du = F(g(u))Ig-l(a)
g-l(a)
F(g(g-l(b)))
-
F(g(g-l(a)))
F(b) - F(a). (1.21)
