Stefanica D. A Primer for the Mathematics of Financial Engineering

224

CHAPTER

7.

MULTIVARIABLE

CALCULUS.

oV

ot

1

ow

(J"2

ow

2

OT

By

substituting

in (7.30), we

obtain

the

following

PDE

satisfied by

w(x,

T):

(J"2

ow

(J"2

2 1

(02W

ow)

1

ow

- 2

OT

+ 2

S

.

S2

ox2 -

ox

+

(r-q)S·s

ox

-

rw

=

O.

(7.39)

After

canceling

out

the

terms

involving S

and

dividing by -

~2,

the

PDE

(7.39) becomes

2

(r

-

q))

ow

2r

_ 0

2

~

+

2W-.

(J" uX (J"

(7.40)

The

PDE

(7.40) satisfied by

the

function

w(x,

T)

has

constant

coefficients

and

is forward parabolic. To eliminate

the

lower order terms, i.e.,

the

terms

corresponding

to

~~

and

w, let

w(x,

T)

= exp(

-ax

- bT)U(X, T),

where a

and

b are

constants

to

be

determined later.

It

is easy

to

see

that

ow

exp(

-ax

-

bT)

oX

(-au

8U)

+

ox

;

02w

exp(

-ax

-

bT)

( a

2

u

ox

2

ou

2a-

ox

+

ow

exp(

-ax

-

bT)

(-bU

+

~~).

OT

8

2

u)

ox

2

'

Therefore,

the

PDE

(7.40) for

w(x,

T)

becomes

the

following

PDE

for

u(x,

T):

ou

02U

(

2(r

-

q))

ou

~

-

~

2 + 2a + 1 - 2

~

uT uX (J" uX

- (

b+

a

2

+ a ( 1 - 2 (r

<T~

q))

-

!:)

U

O.

7.B.

BARRIER

OPTIONS

225

We choose

the

constants

a

and

b is such a way

that

the

coefficients of

~~

and

u are equal

to

0, i.e., such

that

{

2a + 1 - 2(r-;-q) = 0

b + a

2

+ a

(1

- 2(r-

q

))

:.

2r

= 0

0-

2

0-

2

The

solution of

this

system

is given

by

(7.35-7.36); see

an

exercise

at

the

end

of this chapter.

Thus,

using

the

change of variables (7.32),

the

Black-Scholes

PDE

(7.30) for V(S, t) becomes

the

heat

equation

for

u(x,

T),

i.e.,

ou

02u

OT

- ox2 =

O.

While

this

is all we

wanted

to

show here, we

note

that

we can use

the

same

change

of

variables

to

transform

the

boundary

conditions V(S,

T)

into bound-

ary

conditions

u(x,

0) for

the

heat

equation. A closed formula for solving

the

heat

equation

with

boundary

conditions

at

time

t = 0 exists. Therefore,

closed formulas for

u(x,

T)

can

be

obtained, and, from (7.32), closed formulas

for

V(S, t)

can

then

be

inferred.

If

the

boundary

conditions for V(S,

T)

are

chosen

to

correspond

to

those for

European

call or

put

options payoffs

at

time

T,

then

the

Black-Scholes formulas (3.57)

and

(3.58), previously derived in

section 4.7

by

using

risk-neutral

pricing, are obtained.

7.8

Barrier

options

An

exotic

option

is

any

option

that

is

not

a plain vanilla option. Some exotic

options

are

path-dependent:

the

value of

the

option

depends

not

only on

the

value of

the

underlying asset

at

maturity,

but

also

on

the

path

followed by

the

price

of

the

asset between

the

inception of

the

option

and

maturity.

It

rarely

happens

to

have closed formulas for pricing exotic options. How-

ever,

European

barrier

options are

path-dependent

options for which closed

form pricing formulas exist. A barrier

option

is different from a plain vanilla

option

due

to

the

existence

of

a barrier B:

the

option

either

expires worth-

less

(knock-out

options),

or

becomes a plain vanilla

option

(knock-in

options)

if

the

price of

the

underlying asset

hits

the

barrier

before maturity.

Depending

on

whether

the

barrier

must

be

hit

from below

or

from above

in

order

to

be

triggered,

an

option

is called

up

or

down.

Every option can be

either a call

or

a

put

option, so

there

are,

at

the

first count,

at

least eight

different

types

of options:

up

in

put

down out call

226

CHAPTER

7.

MULTIVARIABLE

CALCULUS.

This

should

be

read

as follows: choose

one

entry

in

each column, e.g.,

up,

out,

call.

This

option

is

an

up-and-out

call, which expires worthless

if

the

price

of

the

underlying asset

hits

the

barrier

B from below,

or

has

the

same

payoff

at

maturity

as a call

option

with

strike K otherwise.

The

position

of

the

strike K relative

to

the

barrier

B is also

important.

If

the

spot

price

8(0)

of

the

underlying asset

at

time

0 is such

that

the

barrier

is

already

triggered,

then

the

option

is

either

worth

0,

or

it

is equivalent

to

a

plain

vanilla option, which is priced using

the

Black-Scholes formula.

There-

fore, we

are

interested

in

the

case

when

the

barrier

is

not

trigerred

already

at

time

O.

There

are

sixteen different

barrier

options

to

price, corresponding

to

up

in

put

B < K

down out call B

~

K

Several

barrier

options

can

be

priced

by

using simple

no-arbitrage

argu-

ments,

either

in

an

absolute way,

or

relative

to

other

barrier

options.

For example, long positions

in

one

up-and-out

and

one up--and-in

option

with

all

other

parameters,

i.e.,

barrier,

maturity,

and

strike of

the

underlying

option,

being

the

same

is equivalent

to

a long position

in

the

corresponding

plain

vanilla option.

It

is easy

to

see

that

for every possible

path

for

the

price

of

the

underlying asset,

the

final payoffs

of

the

plain vanilla

option

and

of

a

portfolio

made

of

the

up-and-out

and

the

up-and-in

options

are

the

same:

If

the

barrier

is

hit

before

the

expiry

of

the

options,

then

the

up-and-out

option

expires worthless, while

the

up-and-in

option

becomes a plain vanilla

option.

Thus,

the

payoff of

the

portfolio

at

maturity

will

be

the

same

as

the

payoff

of

a

plain

vanilla option.

If

the

price

of

the

underlying asset never reaches

the

barrier,

then

the

up-and-

in

option

is never knocked in,

and

will expire worthless, while

the

up-and-out

option

is never knocked

out,

and

it

will have

the

same

payoff

at

maturity

as

a

plain

vanilla option.

The

payoff

at

maturity

of

the

portfolio

made

of

the

barrier

options

will

be

the

same

as

the

payoff

of

a plain vanilla option.

Similarly, we

can

show

that

a portfolio

made

of

a

down-and-out

and

a

down-and-in

option

is equivalent

to

a

plain

vanilla option.

This

means

that

we only have

to

price

either

the

"in"

or

the

"out" option;

the

complementary

option

can

be

priced using

the

Black-Scholes formula for

pricing

plain

vanilla options.

The

following

knock-out

barrier

options

have value

0:

•

up-and-out

call

with

8(0)

< B

:s:

K;

•

down-and-out

put

with

8(0)

> B >

K,

since

the

barrier

must

be

triggered,

and

therefore

the

option

will

be

knocked

out,

in

order

for

the

underlying

option

to

expire

in

the

money.

Using

the

"in"-"out"

duality, we conclude

that

the

following

knock-in

options

have

the

same

value as

the

corresponding plain vanilla options:

7.S.

BARRIER

OPTIONS

227

•

the

up-and-in

call

with

8(0)

:s:

B

:s:

K;

•

the

down-and-in

put

with

8(0)

> B >

K.

For all

the

options

listed above,

the

barrier

must

be

triggered

in

order

for

the

option

to

expire

in

the

money.

Therefore,

it

is

enough

to

price

the

following

barrier

options:

1.

up-and-in

call

with

B >

K;

2.

down-and-in

call

with

B >

K;

3.

down-and-in

call

with

B <

K;

4.

up-and-in

put

with

B >

K;

5.

up-and-in

put

with

B <

K;

6.

down-and-in

put

with

B <

K.

Closed formulas for pricing

these

types

of

barrier

options

can

be found

in

Haug

[12].

For example,

the

value

of

the

down-and-out

call

with

B < K is

V(8,K,t)

(

B)2a

(B2

)

C(8,K,t)

- 8 C

S,K,t

,

(7.41)

where

the

constant

a is given

by

formula (7.35), i.e., a =

r~q

-~.

Here,

C(8, K, t) is

the

value

at

time

t

of

a plain vanilla call

option

with

strike K

on

the

same

underlying

asset, C (

~2

,

K,

t)

is

the

Black-Scholes value

at

time

t

of

a

plain

vanilla call

with

strike K

on

an

asset having

spot

price

~

(and

the

same

volatility as

the

underlying).

Note

that,

as expected, V(8, K, t) <

C(8,K,t).

Also,

V(8,K,t)

~

C(8,K,t)

as

the

barrier

B goes

to

0, when

the

probability

of

hitting

the

barrier

and

knocking

the

option

out

also goes

to

0:

lim V(8, t) = C(8, t).

B"'.O

As expected, closed formulas do

not

exist for pricing American barrier

options. Numerical

methods,

e.g., binomial

tree

methods

and

finite differ-

ences,

are

used

to

price American

barrier

options.

From

the

point of view

of

computational

costs,

the

solutions

of

the

numerical

methods

for

barrier

options

are

comparable

to

those

for plain vanilla options, for finite difference

methods,

and

more

expensive for

tree

methods.

228

7.9

CHAPTER

7.

MULTIVARIABLE

CALCULUS.

On

the

optimality

of

early

exercise

for

American

options

It

is

interesting

to

note

that

American

call

options

on

non-dividend

paying

assets

are

never

optimal

to

exercise.

Instead

of

exercising

the

call,

entering

into

a

static

hedge

by

shorting one

unit

of

the

underlying asset is

guaran-

teed

to

be

more

profitable.

American

calls

on

non-dividend

paying assets

are

therefore

worth

the

same

as

the

corresponding

European

calls.

This

is

not

true

for American

put

options,

nor

for American calls

on

assets paying

dividends.

To see this, assume

that,

at

time

t <

T,

the

call

option

is in

the

money,

i.e., S(t) > K; here T denotes

the

maturity

of

~he

option

..

For

the

long

~all

position

(i.e., for

the

holder of

the

option), consIder two dIfferent strategIes:

First Strategy: Exercise

the

call

at

time

t

and

deposit

the

premium

S(t) - K

at

the

constant

risk free

rate

r

until

time

T.

The

value

of

the

resulting

portfolio

at

time

T is

Vt(T) = (S(t) -

K)

er(T-t);

(7.42)

Second Strategy: Do

not

exercise

the

call;

short

one

unit

of

the

underlying

asset

at

time

t,

and

wait until

maturity

T

without

exercising

the

American

option.

At

time

t,

the

portfolio will consist

of:

• long 1 American call;

•

short

1

unit

of

the

underlying asset;

•

cash

S(t). . .

The

value

of

this

portfolio

at

time

T

depends

on

whether

the

call expIres

III

the

money

or

not:

If

S(T)

>

K,

then

the

call is exercised

at

time

T,

and

K is

p~~d

for one

unit

of

the

underlying asset, which is used

to

close

the

short

posItIOn.

The

cash

position

of

S

(t)

at

time

t

earns

interest

at

the

constant

risk free

rate

r.

Its

value

at

time

Tis

S(t)er(T-t).

The

value

of

the

portfolio will

be

112,1

(T) = S( t)

er(T-t)

- K.

(7.43)

If

S(T)

::;

K,

then

the

call expires worthless.

One

unit

is

of

the

~~derlying

asset is

bought

at

time

T, for

the

price S(T),

to

close

the

short

posItIOn.

The

value

of

the

portfolio will

be

V2,2(T)

= S(t)

er(T-t)

-

S(T)

~

S(t)

er(T-t)

- K,

(7.44)

since

S(T)

::;

K

in

this

case.

From

(7.43)

and

(7.44), we conclude

that,

if

the

second

strategy

is used,

the

value of

the

portfolio

at

time

T is

guaranteed

to

be

at

least

V2(T)

= min(V2,1(T),V2,2(T)) = S(t)

er(T-t)

- K.

(7.45)

7.9.

OPTIMALITY

OF

EARLY

EXERCISE

229

Note

that

S(t)

er(T-t)

- K > (S(t) -

K)

er(T-t)

,

(7.46)

provided

that

the

interest

rates

are

positive, i.e.,

that

r >

O.

From

(7.42),

(7.45),

and

(7.46) we conclude

that

the

value

of

the

second portfolio, i.e.,

of

the

static

hedging strategy, is higher

than

the

value

of

the

portfolio if

the

option

is exercised

at

time

t before maturity, i.e.,

V2(T)

> Vt(T).

In

other

words,

it

is never

optimal

to

exercise

early

an

American call

option

on

a

non-dividend

paying asset.

Shorting

the

underlying asset

and

holding

the

American

call

option

until

maturity

will

earn

a

greater

payoff

at

maturity

than

exercising

the

call

option

early.

It

is

natural

to

ask

why does

the

not

hold if

the

un-

derlying asset pays dividends,

and

for

put

options?

When

shorting

a dividend paying asset, you

are

responsible for paying

the

dividends

to

the

lender

of

the

asset. Therefore, if

the

static

hedge

strategy

is

employed,

the

value

of

the

portfolio

at

time

T will

be

reduced

by

the

amount

of

the

dividends paid.

Then,

if

the

call

option

expires

in

the

money, all we

can

say7 is

that

V2,1(T)

< S(t)

er(T-t)

- K,

which no longer

means

that

Vt(T) = (S(t) - K)er(T-t) <

112,1

(T).

In

other

words,

the

static

hedging

strategy

of

shorting

the

underlying asset is no longer

guaranteed

to

be

worth

more

at

time

T

than

the

strategy

of

exercising

the

call

at

time

t.

For

an

American

put

option

which is

in

the

money

at

time

t, i.e., S(t) <

K,

exercising

the

option

and

holding

the

cash

until

maturity

T generates

the

following payoff

at

time

T:

~(T)

=

(K

- S(t))

er(T-t).

The

static

hedging

strategy

for

the

long

put

position is

to

buy

one

unit

of

the

underlying

asset (paying S(t) cash

to

do so).

At

time

t,

the

portfolio

will consist

of

long 1 American

put,

long 1

unit

of

the

underlying asset,

and

- S ( t)

in

cash.

In

this

case,

the

interest

earned

by

the

cash

borrowed

to

buy

the

asset reduces

the

value

of

the

portfolio.

(This

is similar

to

the

role played

by

dividends for

the

static

hedging

of

American call options.)

If

the

put

expires

in

the

money, i.e., if

S(T)

<

K,

then

it

is exercised,

and

the

share

will

be

sold for

K.

The

value

of

the

portfolio

in

this

case is

7If

the

underlying asset pays dividends continuously

at

the

rate

q,

it

can

be

shown

that

V2,l(T) = S(t)

e(r-q)(T-t)

- K.

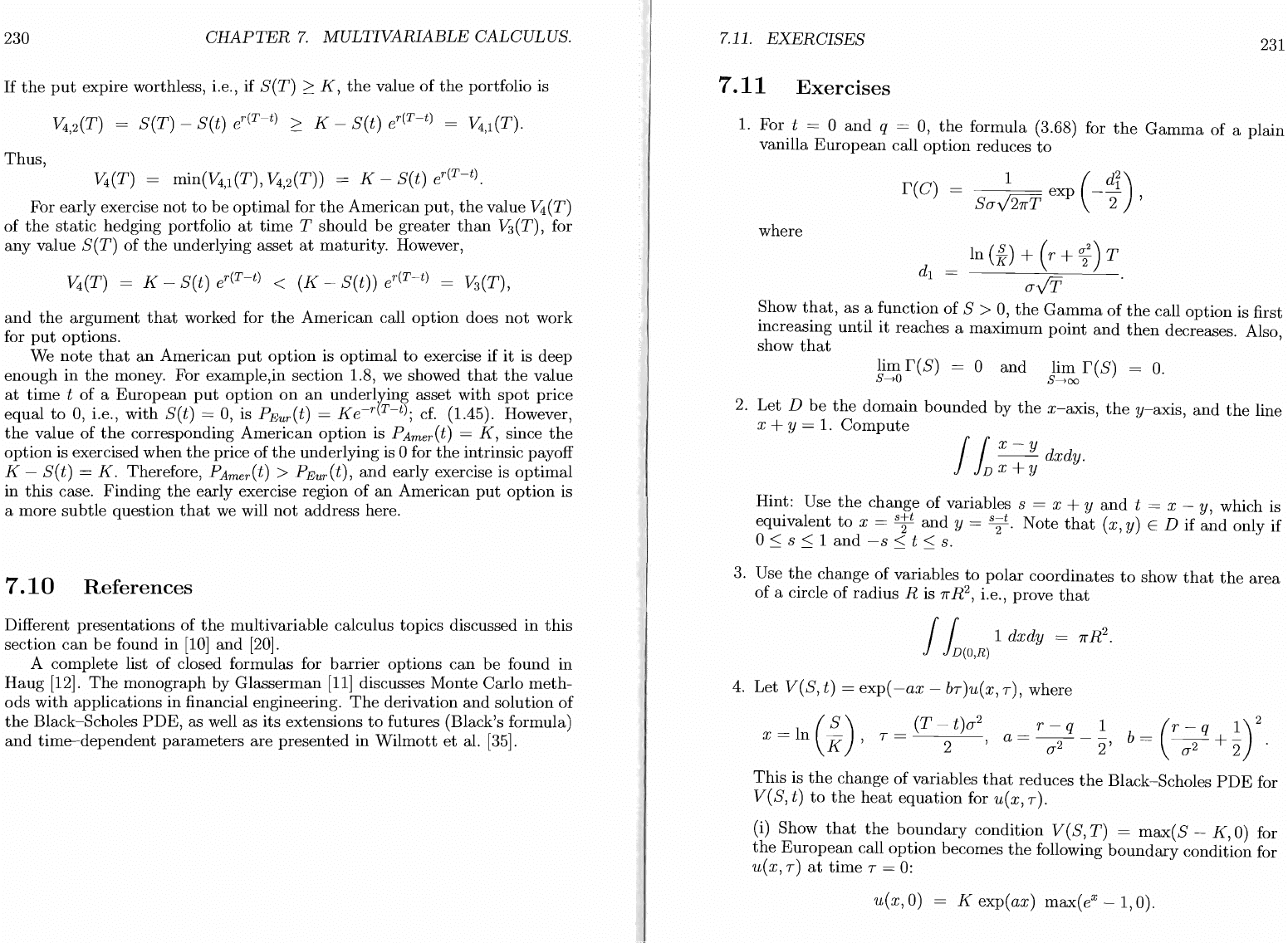
230

CHAPTER

7.

MULTIVARIABLE

CALCULUS.

If

the

put

expire worthless, i.e., if S(T)

;::::

K,

the

value

of

the

portfolio is

V4,2(T)

= S(T) - S(t)

er(T-t)

;::::

K - S(t)

er(T-t)

= V4,l(T).

Thus,

V4(T)

= min(V4,l(T),

Y4,2(T))

= K - S(t)

er(T-t).

For early exercise

not

to

be

optimal

for

the

American

put,

the

value

V4(T)

of

the

static

hedging portfolio

at

time

T should

be

greater

than

1I3(T)

, for

any

value S(T) of

the

underlying asset

at

maturity. However,

V4(T)

= K - S(t)

er(T-t)

<

(K

- S(t))

er(T-t)

=

1I3(T)

,

and

the

argument

that

worked for

the

American call

option

does

not

work

for

put

options.

We

note

that

an

American

put

option

is

optimal

to

exercise if

it

is deep

enough

in

the

money. For example,in section 1.8, we showed

that

the

value

at

time

t

of.

a Eu::opean

put

o~tion

on

an

und~;~~f

asset

with

spot

price

equal

to

0, l.e., w1th S(t) = 0,

1S

PEur(t)

=

Ke

),

cf.

(1.45).

However,

the

value of

the

corresponding American

option

is

PAmer(t)

=

K,

since

the

option

is exercised when

the

price of

the

underlying is 0 for

the

intrinsic payoff

K - S(t) =

K.

Therefore,

PAmer(t)

>

PEur(t),

and

early

~xercise

is

op~im~l

in

this

case.

Finding

the

early exercise region

of

an

Amencan

put

optlOn

IS

a more

subtle

question

that

we

will

not

address here.

7.10

References

Different presentations of

the

multivariable calculus topics discussed

in

this

section

can

be

found

in

[10]

and

[20].

A complete list of closed formulas for

barrier

options

can

be

found

in

Haug

[12].

The

monograph by Glasserman

[11]

discusses Monte Carlo

meth-

ods

with

applications in financial engineering.

The

derivation

and

solution

of

the

Black-Scholes

PDE,

as well as its extensions

to

futures (Black's formula)

and

time-dependent

parameters

are presented

in

Wilmott

et

al.

[35].

7.11.

EXERCISES

231

7.11

Exercises

1.

For t = 0

and

q = 0,

the

formula (3.68) for

the

Gamma

of a plain

vanilla

European

call option reduces

to

1 ( d

i

)

r(

C) =

S(JV27rT

exp

-2

'

where

In

(f)

+

(r

+

~2)

T

d

1

=

(JVT

Show

that,

as a function

of

S > 0,

the

Gamma

of

the

call option is first

increasing

until

it

reaches a

maximum

point

and

then

decreases. Also,

show

that

lim

r(S)

= 0

and

lim

r(S)

=

O.

8--+0 8--+00

2.

Let D

be

the

domain

bounded

by

the

x-axis,

the

y-axis,

and

the

line

x + y =

1.

Compute

11

x-y

.

--

dxdy.

DX+Y

Hint: Use

the

change of variables s = x + y

and

t = x - y, which is

equivalent

to

x =

stt

and

y =

s-:;,t.

Note

that

(x, y) E D if

and

only if

o

::s:

s

::s:

1

and

- s

::s:

t

::s:

s.

3.

Use

the

change of variables

to

polar coordinates

to

show

that

the

area

of a circle

of

radius

R is

7rR

2

,

i.e., prove

that

1

r 1

dxdy

=

7rR2.

JD(O,R)

4.

Let V(S, t) =

exp(

-ax

-

bT)U(X,

T),

where

_ I

(~)

_ (T -

t)(J2

_ r - q _

~

x - n K ' T - 2

,a

-

(J2

2 '

This

is

the

change of variables

that

reduces

the

Black-Scholes

PDE

for

V(S, t)

to

the

heat

equation for

u(x,

T).

(i) Show

that

the

boundary

condition V(S, T) = max(S -

K,O)

for

the

European

call

option

becomes

the

following

boundary

condition for

u(x,

T)

at

time

T =

0:

u(x,O)

= K

exp(ax)

max(e

X

-

1,0).

232

CHAPTER

7.

MULTIVARIABLE

CALCULUS.

(ii) Show

that

the

boundary

condition

V(S,

T)

=

max(K

- S, 0) for

the

European

put

option

becomes

u(x,O) = K exp(ax)

max(1

-

eX,

0).

5. Show

that

the

solution of

the

system

{

2a

+ 1 _

2(r-q)

b+a

2

+a

(1-

2(:~q))

-"';~

. _

r-q

1 d b _

(r-

q

1)

2

IS

a -

~

-

"2

an

- (7"2 + 2 .

Note:

An

elegant way

to

do

this

is

to

notice

that

2

(r-

q

1)

2(r-q)

b+a

-2a

----

-

(j2

2

(j2

o

b+(a-(r;2q-Dr

-

(r~q_D2

r-q

1

r-q

1

))

2 (

)2

b+(a-(~-2

-

~+2

2(r -

q)

(j2

6.

Assume

that

the

function

V(S,

I,

t) satisfies

the

following

PDE:

av

1 2 2

a2v

av

V 0

at

+ S

aI

+ 2(j S

aS

2

+ r S

as

- r = .

(7.47)

Consider

the

following change

of

variables:

V(S,

I,

t) = S

H(R,

t), where R

(7.48)

Show

that

H(R,

t) satisfies

the

following

PDE:

aH

1 2R

2a2H

(

R)

aH

0

at

+ 2(j aR2 + 1 - r

aR

= .

(7.49)

Note:

An

Asian call

option

pays

the

maximum

between

the

spot

price

S(T)

of

the

underlying asset

at

maturity

T

and

the

average price

of

the

underlying asset over

the

entire

life of

the

option, i.e.,

mme

(8(T)

-

~

[ 8(T) dT) .

7.11.

EXERCISES

233

Thus,

the

price

V(S,

I,

t) of

an

Asian

option

depends

not

only on

the

spot

price S

of

the

underlying asset

and

on

the

time

t,

but

also

on

the

average price

I(t)

of

the

underlying between

time

0

and

time

t, where

I(t) =

l'

8(T)

dT.

It

can

be

shown

that

V(S,

I,

t) satisfies

the

PDE

(7.47). Similarity

solutions

of

the

type

(7.48)

are

good

candidates

for solving

the

PDE

(7.47).

The

PDE

(7.49) satisfied by

H(R,

T)

can

be

solved numerically,

e.g.,

by

using finite differences.

7.

The

price

of

a non-dividend-paying asset is lognormally distributed.

Assume

that

the

spot

price is 40,

the

volatility is 30%,

and

the

interest

rates

are

constant

at

5%. Fill

in

the

Black-Scholes values of

the

OTM

put

options

on

the

asset

in

the

table

below:

Option

Type

Strike

Maturity

Value

Put

45 6

months

Put

45 3

months

Put

48 6

months

Put

48 3

months

Put

51

6

months

Put

51

3

months

For which

of

these

options is

the

intrinsic value

max(K

- S,O) larger

than

the

price

of

the

option

(in which case

the

corresponding American

put

is

guaranteed

to

be

worth

more

than

the

European

put)?

8.

Show

that

the

premium

of

the

price

of

a

European

call

option

over

its

intrinsic value

max(S

-

K,

0)

is largest

at

the

money.

In

other

words,

show

that

the

maximum

value

of

CBS(S) -

max(S

- K,O)

is

obtained

for S =

K,

where CBS(S) is

the

Black-Scholes value

of

the

plain

vanilla

European

call

option

with

strike K

and

spot

price S.

9.

Use formula (7.41)

to

price a six

months

down-and-out

call

on

a

non-

dividend-paying

asset

with

price following a lognormal

distribution

with

30% volatility

and

spot

price 40.

The

barrier

is B = 35

and

the

strike for

the

call is K = 40.

The

risk-free

interest

rate

is

constant

at

5%.

234

CHAPTER

7.

MULTIVARIABLE

CALCULUS.

10. Show

that

the

value

of

a

down-and-out

call

with

barrier

B less

than

the

strike K

of

the

call, i.e., B <

K,

converges

to

the

value

of

a

plain

vanilla call

with

strike K when B

~

O.

For simplicity, assume

that

the

underlying asset does

not

pay

dividends

and

that

interest

rates

are

zero.

Hint: Use formula (7.41)

to

show

that

the

value

of

the

down-and-out

call is

V(8, t) = C(8, t) -

(BN(d

1

) -

81~

e-

rT

N(d2)) ,

where C (S, t) is

the

value

of

the

plain

vanilla call

with

strike K

and

Use

l'Hopital's

rule

to

show

that

. 1

hm

-

N(d

2

)

B'\,oB

o.

(

B2 )

(J2T

In

SK

- 2

aVT

11.

Compute

the

Delta

and

Gamma

of

a

down-and-out

call

with

B <

K,

using formula (7.41).

Chapter

8

Lagrange

multipliers.

N-

dimensional

Newton's

method.

Implied

volatility.

Bootstrapping.

The

Lagrange multipliers

method

for finding

absolute

extrema

of

multivari-

able functions.

Newton's

method,

bisection

method,

and

secant

method

for solving one di-

mensional

nonlinear

problems.

Newton's

method

for solving

N-dimensional

nonlinear problems.

8.1

Lagrange

multipliers

Optimization

problems

often

require finding

extrema

of

multivariable func-

tions

subject

to

various constraints.

One

method

to

solve such problems is

by

using

Lagrange

multipliers, as outlined below.

Let U c

~n

be

an

open

set,

and

let

j : U

-----7

~

be

a

smooth

function, e.g.,

infinitely

many

times

differentiable. We

want

to

find

the

extrema

of

j (x)

subject

to

m

constrains

given

by

g(x) = 0, where 9 : U

-----7

~m

is a

smooth

function, i.e.,

Find

Xo

E U such

that

max

j(x)

= j(xo)

g(x) = 0

xEU

or

min

j(x)

g(x) = 0

xEU

j(xo).

(8.1)

Problem

(8.1) is called a constrained

optimization

problem. For

this

prob-

lem

to

be

well posed, a

natural

assumption

is

that

the

number

of

constraints

is smaller

than

the

number

of

degrees of freedom, i.e., m < n.

Another

way

to

formalize problem (8.1) is

to

introduce

the

set S of

points

satisfying

the

constraint

g(

x)

=

0,

and

find

extrema

for

the

restriction

of

the

function j (x)

to

the

space

S,

i.e., for j

Is.

235

236

CHAPTER

8.

LAGRANGE

MULTIPLIERS.

NEWTON'S

METHOD.

Definition

8.1.

The point

Xo

E U c

IR

n

is called a constrained extremum

of

the function f : U

-----+

IR

with respect to the constraint

g(

x) = 0

if

and only

if

Xo

is an extremum point

of

fls,

where S =

{x

E U such that g(x) = o}.

To

solve

the

constrained

optimization

problem

(8.1), let A =

(Ai)i=l:m

be

a

vector

of

the

same

size,

m,

as

the

number

of

constraints; A is called a

Lagrange

multipliers vector.

Let

F : U x

IR

m

-----+

IR

given

by

F(x,

A)

=

f(x)

+

At

g(x)

be

the

Lagrangian

function

of

f

and

g.

If

then

F (

x,

A)

can

be

written

explicitly as

It

is

easy

to

see

that

8F

8X.(X,A)

J

8F

8Ai (x,

A)

m

F(x,

A)

=

f(x)

+ L Aigi(X).

i=l

= gi(X),

\I

i = 1 :

m.

(8.2)

(8.3)

(8.4)

The

gradient

1

of

F(x,

A)

with

respect

to

both

x

and

A will

be

denoted

by

V(X,A)

F(x,

A),

and

is

the

following row vector:

V(X,A)

F(x,

A)

= ( V x

F(x,

A)

VA

F(x,

A)

);

(8.5)

cf. (1.36).

From

(8.3)

and

(8.4)

it

follows

that

Vx

F(x,

A)

(

8F

8X1

(x,

A)

-(X,A)

=

Vf(x)

+ (Vg(X))tA;

(8.6)

8F

)

8x

n

VA

F(X,A)

(

8F

8A1

(x,

A)

-(x,

A)

= g(x),

(8.7)

8F

)

8A

m

1

In

this

section,

we

use

the

notation

V

F,

instead

of

D

F,

for

the

gradient of F.

8.1.

LAGRANGE

MULTIPLIERS

237

where

Vf(x)

and

Vg(x),

the

gradients of f : U

-----+

IR

and

9 : U

-----+

IRm

are

given by

v

f(x)

(:;,

(x,

>.)

...

::n

(x,

>.))

;

(

~;~

(x)

~;~

(x)

...

~;~

(x) )

Og2

(x)

Og2

(x) '"

Og2

(x)

Vg(x)

OXl.

OX2

. .

OXn.

;

. . . .

. .

ogm

(x)

ogm

(x)

ogm

(x)

OXl

OX2

OXn

cf. (1.36)

and

(1.38), respectively. From (8.5-8.7), we conclude

that

V(X,A)

F(x,

A)

=

(Vf(x)+(Vg(x))tA

g(x)).

(8.8)

In

the

Lagrange multipliers

method,

the

constrained

extremum

point

Xo

is found

by

identifying

the

critical points

of

the

Lagrangian

F(x,

A).

For

the

method

to

work,

the

following condition

must

be

satisfied:

The gradient V

g(

x)

has full rank at any point x in the constrained space

S,

i.e.,

rank(Vg(x))

= m,

\I

XES.

(8.9)

The

following

theorem

gives necessary conditions for a

point

Xo

E U

to

be

a constrained

extremum

point

for f (

x).

Its

proof

involves

the

inverse function

theorem

and

is

beyond

the

scope of this book.

Theorem

8.1.

Assume that the constraint function g(

x)

satisfies the condi-

tion

{8.9}.

If

Xo

E U is a constrained extremum

of

f(x)

with respect to the

constraint

g(

x)

=

0,

then there exists a Lagrange multiplier

AO

E

IRm

such

that the point (xo,

AO)

is a critical point for the Lagrangian function

F(x,

A),

i.

e., such that

V(X,A)

F(xo,

AO)

=

o.

(8.10)

We

note

that

V(X,A)

F(x,

A)

is a function from

IRm+n

into

IRm+n.

Thus,

solving (8.10)

to

find

the

critical

points

of

F(x,

A)

requires,

in

general, using

the

N-dimensional

Newton's

method

for solving nonlinear equations. Inter-

estingly enough, for some practical problems such as finding efficient portfo-

lios,

problem

(8.10) is

actually

a linear

system

which

can

be

solved

without

using

Newton's

method;

see section 8.4 for details.

If

condition (8.9) is

not

satisfied,

then

Theorem

8.1 does

not

necessarily

hold, as seen

in

the

example below:

Example:

Find

the

minimum

of

XI

+

Xl

+

x§,

subject

to

the

constraint

(Xl

-

X2?

=

o.

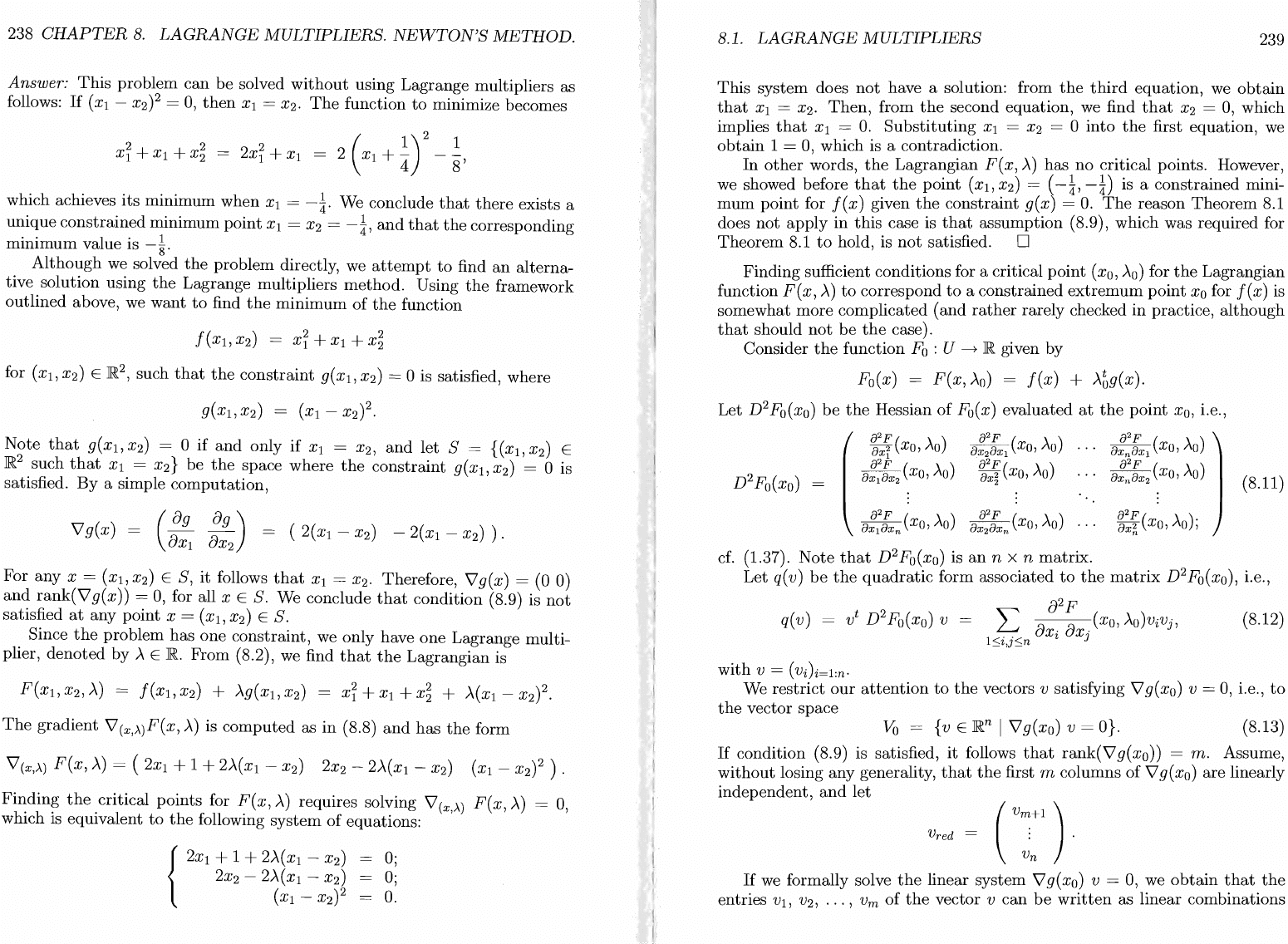
238

CHAPTER

B.

LAGRANGE

MULTIPLIERS.

NEWTON'S

METHOD.

Answer:

This

problem can

be

solved

without

using Lagrange multipliers as

follows:

If

(Xl

-

X2)2

=

0,

then

Xl

=

X2.

The

function

to

minimize becomes

which achieves

its

minimum when

Xl

=

-~.

We conclude

that

there

exists a

unique constrained minimum

point

Xl

=

X2

=

-~,

and

that

the

corresponding

minimum

value is

-~.

Although

we solved

the

problem directly, we

attempt

to

find

an

alterna-

tive solution using

the

Lagrange multipliers

method.

Using

the

framework

outlined above, we

want

to

find

the

minimum

of

the

function

f(Xl,

X2)

=

xi

+

Xl

+

x~

for (Xl,

X2)

E

JR2,

such

that

the

constraint

g(Xl,

X2)

= ° is satisfied, where

g(Xl,X2) =

(Xl

-

X2)2.

Note

that

g(Xl,

X2)

= ° if

and

only if

Xl

=

X2,

and

let

S = {(Xl,

X2)

E

JR2 such

that

Xl

=

X2}

be

the

space where

the

constraint g(Xl'

X2)

= ° is

satisfied.

By

a simple computation,

For

any

X = (Xl,

X2)

E

S,

it

follows

that

Xl

=

X2.

Therefore,

\l

g(x) = (0 0)

and

rank(\lg(x))

=

0,

for all

xES.

We conclude

that

condition (8.9) is

not

satisfied

at

any

point X = (Xl,

X2)

E S.

Since

the

problem

has

one constraint, we only have one Lagrange multi-

plier, denoted by

A E JR. From (8.2), we find

that

the

Lagrangian is

F(xl,

X2,

A)

= f(Xl,

X2)

+ Ag(Xl,

X2)

=

xi

+

Xl

+

x~

+

A(XI

-

X2)2.

The

gradient

\l(x,)..)F(x,

A)

is

computed

as

in

(8.8)

and

has

the

form

\l(x,)..)

F(x,

A)

= (

2Xl

+ 1 +

2A(XI

-

X2)

2X2

- 2A(XI -

X2)

(Xl

-

X2)2

) .

Finding

the

critical points for

F(x,

A)

requires solving

\l(x,)..)

F(x,

A)

= 0,

which is equivalent

to

the

following

system

of

equations:

B.l.

LAGRANGE

MULTIPLIERS

239

This

system does

not

have a solution: from

the

third

equation, we

obtain

that

Xl

=

X2.

Then,

from

the

second equation, we find

that

X2

= 0, which

implies

that

Xl

=

0.

Substituting

Xl

=

X2

= ° into

the

first equation, we

obtain

1 = 0, which is a contradiction.

In

other

words,

the

Lagrangian

F(x,

A)

has

no critical points. However,

we showed before

that

the

point (Xl,

X2)

=

(-~,

-~)

is a constrained mini-

mum

point

for

f(x)

given

the

constraint g(x) = 0.

The

reason

Theorem

8.1

does

not

apply

in

this

case is

that

assumption (8.9), which was required for

Theorem

8.1

to

hold, is

not

satisfied. D

Finding sufficient conditions for a critical

point

(xo,

AO)

for

the

Lagrangian

function

F ( x,

A)

to

correspond

to

a constrained

extremum

point

Xo

for f ( x) is

somewhat more complicated (and

rather

rarely checked in practice, although

that

should

not

be

the

case).

Consider

the

function

Fo

: U ----7 JR given by

Fo(x) =

F(x,

AO)

=

f(x)

+

Agg(X).

Let

D2

Fo(xo)

be

the

Hessian of Fo(x) evaluated

at

the

point

Xo,

i.e.,

(PF

)

8

2

F (

A)

8

2

F (

A)

p(XO,Ao

8X28xI

Xo,

0

8x

n

8x

I

Xo,

0

Xl

8

2

F (

A)

8

2

F ( )

8

2

F (

A)

D2

Fo(xo)

8Xl8x2

Xo,

0

8x2

XO,

AO

8x

n

8x

2

Xo,

0

(8.11)

2

8

2

F (

A)

8x

l

8x

n

Xo,

0

8

2

F ( )

~

Xo,AO

X2

x"

8

2

F(

).

8x~

xo,

AO

,

cf. (1.37). Note

that

D2

Fo(xo) is

an

n x n matrix.

Let

q(

v)

be

the

quadratic

form associated

to

the

matrix

D2

Fo(xo), i.e.,

(8.12)

with

v =

(Vi)i=l:n'

We restrict

our

attention

to

the

vectors v satisfying

\l

g(xo) v =

0,

i.e.,

to

the

vector space

Va

= {v E

JRn

I \lg(xo) v =

O}.

(8.13)

If

condition (8.9) is satisfied,

it

follows

that

rank(\l

g(xo)) = m. Assume,

without

losing

any

generality,

that

the

first m columns of

\l

g(xo) are linearly

independent,

and

let

If

we formally solve

the

linear system

\l

g(xo) v = 0, we

obtain

that

the

entries

VI,

V2,

...

,

Vm

of

the

vector v can

be

written

as linear combinations

240

CHAPTER

8.

LAGRANGE

MULTIPLIERS.

NEWTON'S

METHOD.

of

Vm+l,

V

m

+2,

...

, V

n

,

the

other

n - m

entries

of

v.

Then,

by

restricting

q(v)

to

the

vector

space

Va,

we

can

write

q(

v)

as a

quadratic

form

depending

only

on

the

entries

of

the

vector

Vred,

i.e.,

L qred(i,j)vivj, \;j v E

Va.

m+ls:i,js:n

(8.14)

Example:

For

clarification

purposes,

we

provide

an

example

of

deriving

the

reduced

quadratic

form

qred(

Vred)

from q( v) for n = 3

and

m = 1.

Assume

that

(

-~ -~

n and

~g(xo)

(1

- 1 2 ).

If

v = (Vi)i=I:3,

then

q(v) = v

t

D;F(xo,

Ao)

v =

v;

+

2v~

+

3v~

-

2VIV2

+

4V2V3.

The

condition

\l

g(xo)v = ° is equivalent

to

VI

-

V2

+

2V3

= 0.

Then,

VI

=

V2

-

2V3

and

q(

v) =

(V2

- 2V3? +

2v~

+

3v~

-

2(

V2

-

2V3)V2

+

4V2V3

=

v~

+

4V2V3

+

7v~.

Note

that

Vred = (

~~

).

The

reduced

quadratic

form

qred(V"d)

is

qred(

Vred)

=

q(

v) =

v~

+

4V2V3

+

7v~.

0

(8.15)

Whether

the

point

Xo

is a

constrained

extremum

for f ( x) will

depend

on

the

quadratic

form

qred

being

either

positive

definite

2

,

i.e.,

or

negative

definite, i.e.,

qred(

Vred)

< 0, \;j

Vred

# 0.

This

result

is

presented

in

the

following

theorem:

example,

the

quadratic

form

qred

from (8.15) is positive definite since

8.1.

LAGRANGE

MULTIPLIERS

241

Theorem

8.2.

Assume

that the constraint function g(x) satisfies condition

( 8.

g).

Let

Xo

E U C

ffi.n

and

Ao

E

ffi.m

such that the point (xo,

Ao)

is a critical

point for the Lagrangian function

F(x,

A)

=

f(x)

+ Ab9(x).

If

the reduced quadratic form (8.14) corresponding to the point (xo,

Ao)

is

positive definite, then

Xo

is

a constrained

minimum

for f (x) with respect to

the constraint g( x)

=

O.

If

the reduced quadratic form (8.14) is negative definite, then

Xo

is a con-

strained

maximum

for

f(x)

with respect to the constraint g(x) = 0.

We

note

that

the

conditions

from

Theorem

8.2 are,

in

practice,

rarely

checked.

While

this

is

not

recommended,

for

some

financial

applications

it

may

be

sound

to

do

so.

The

reason

is

that

if

a

problem

is

known

to

have a

unique

constrained

extremum,

and

if

the

Lagrangian

has

exactly

one

critical

point,

then

that

critical

point

must

be

the

constrained

extremum

point.

For

this

line

of

thinking

to

be

sound

we

must

know

that

the

constrained

extremum

problem

has

a

unique

solution.

In

general, showing

that

a

problem

has

a

unique

solution

is

not

straightforward.

The

steps

required

to

solve a

constrained

optimization

problem

using

Lagrange

multipliers

can

be

summarized

as

follows:

Step

1:

Check

that

rank(\lg(x))

=

m,

for all

xES.

Step

2:

Find

(xo,

Ao)

E U X

ffi.m

such

that

\l(x,)..)F(xo,

Ao)

= 0.

Step

3.1:

Compute

q(v) = v

t

D2

Fo(xo) v,

where

Fo(x) =

f(x)

+ Ab9(x).

Step

3.2:

Compute

qred(

Vred)

by

restricting

q(

v)

to

vectors

v satisfying

the

condition

rank(\l

g(xo))v = 0. Decide

whether

qred(

Vred)

is positive definite

or

negative

definite.

Step

4:

Use

Theorem

8.2

to

decide

whether

Xo

is a

constrained

minimum

point

or

a

constrained

maximum

point.

We

include

two

examples

below.

An

application

of

Lagrange

multipliers

to

portfolio

optimization

is

presented

in

section

8.4.

Example:

Find

the

positive

numbers

xl,

X2,

X3

such

that

XIX2X3

= 1

and

XIX2

+

X2X3

+

X3XI

is minimized.

Answer:

We

first

reformulate

the

problem

as

a

constrained

optimization

problem.

Let

U =

I1i=I:3(0,oo)

C

ffi.3

and

let

x = (XI,X2,X3) E U.

The

functions f : U ----7

ffi.

and

9 : U ----7

ffi.

are

defined as

f(x)

We

want

to

minimize

f(x)

over

the

set

U

subject

to

the

constraint

g(x) = 0.

Step

1:

Check

that

rank(\lg(x))

= 1 for

any

x

such

that

g(x) = 0.

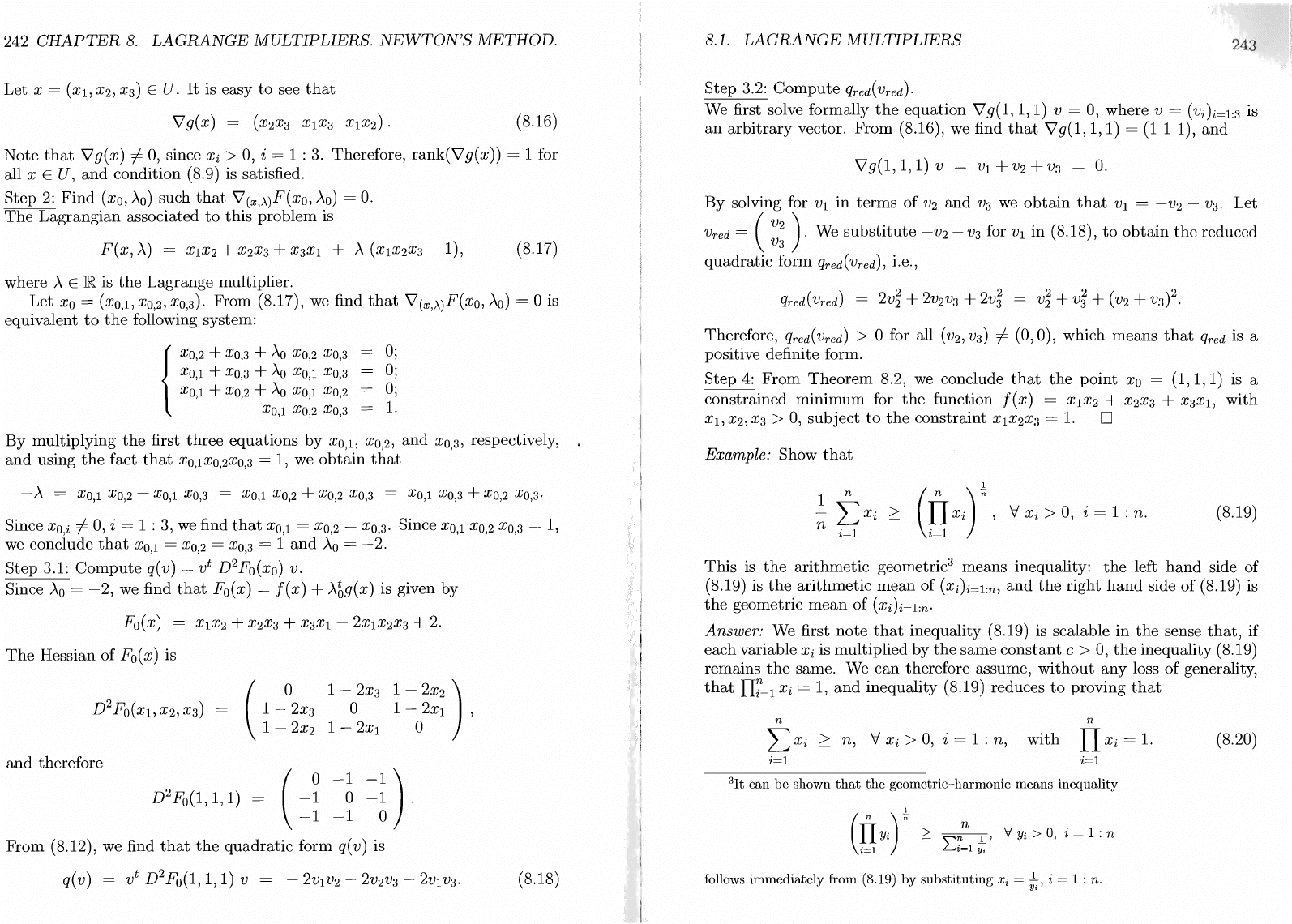
242

CHAPTER

8.

LAGRANGE

MULTIPLIERS.

NEWTON'S

METHOD.

Let

x =

(Xl,

X2,

X3)

E

u.

It

is easy

to

see

that

Vg(x)

=

(X2X3

XIX3

XIX2).

(8.16)

Note

that

\lg(x)

i- 0, since

Xi

> 0, i = 1 : 3. Therefore,

rank(Vg(x))

= 1 for

all

x E U,

and

condition (8.9) is satisfied.

Step

2:

Find

(xo,

Ao)

such

that

V(x,>.)F(xo,

Ao)

= 0.

The

Lagrangian

associated

to

this

problem is

F(x,

A)

=

XIX2

+

X2X3

+

X3Xl

+ A

(XIX2X3

- 1),

where A E

lR

is

the

Lagrange multiplier.

(8.17)

Let

Xo

=

(XO,1,XO,2,XO,3).

From (8.17), we find

that

V(x,>.)F(xo,Ao)

= ° is

equivalent

to

the

following system:

{

XO,2

+

XO,3

+

Ao

XO,2

XO,3

=

0;

XO,l +

XO,3

+

Ao

XO,l XO,3 =

0;

XO,l +

XO,2

+

Ao

XO,l XO,2 = 0;

XO,l

XO,2

XO,3 =

1.

By

multiplying

the

first

three

equations by

XO,l,

XO,2,

and

XO,3, respectively,

and

using

the

fact

that

XO,lXO,2XO,3 =

1,

we

obtain

that

- A = XO,l

XO,2

+ XO,l

XO,3

= XO,l

XO,2

+

XO,2

XO,3

= XO,l

XO,3

+

XO,2

XO,3·

Since

Xo

i i- 0, i = 1 : 3, we find

that

Xo

1 =

X02

=

X03·

Since

Xo

1

X02

x03

we conclude

that

XO,l =

XO,2

=

XO,3

= i

and

~o

= -2.

",

1,

Step

3.1:

Compute

q(v)

= v

t

D

2

F

o

(xo)

v.

Since

Ao

=

-2,

we find

that

Fo(x)

=

f(x)

+

Abg(x)

is given by

Fo(x)

=

XIX2

+

X2X3

+

X3Xl

-

2XIX2X3

+

2.

The

Hessian of F

o

(x)

is

and

therefore

D2

F

o

(1, 1, 1) =

(-

~

-

~

= i ) .

-1 -1

°

From

(8.12), we find

that

the

quadratic

form

q(v)

is

(8.18)

8.1.

LAGRANGE

MULTIPLIERS

243

Step

3.2:

Compute

qred(

Vred).

We first solve formally

the

equation

Vg(l,

1,

1) v = 0, where v =

(Vi)i=1:3

is

an

arbitrary

vector. From (8.16), we find

that

Vg(l,

1,

1) =

(111),

and

v g (1,

1,

1) v =

VI

+ V2 + V3 =

0.

By

solving for

VI

in

terms

of V2

and

V3 we

obtain

that

VI

=

-V2

-

V3.

Let

Vred

= (

~~

).

We

substitute

-V2

- V3 for

VI

in

(8.18),

to

obtain

the

reduced

quadratic

form

qred(

Vred),

i.e.,

Therefore,

qred(Vred)

> ° for all

(V2'

V3)

i- (0,0), which means

that

qred

is a

positive definite form.

Step

4:

From

Theorem

8.2, we conclude

that

the

point

Xo

=

(1,1,1)

is a

constrained

minimum

for

the

function

f(x)

=

XIX2

+

X2X3

+

X3Xl,

with

Xl,

X2,

X3 > 0,

subject

to

the

constraint

XIX2X3

=

1.

D

Example: Show

that

1 n

(n)~

;,

8

Xi

~

g

Xi

,V

Xi

> 0, i = 1 : n.

(8.19)

This

is

the

arithmetic-geometric

3

means inequality:

the

left

hand

side of

(8.19) is

the

arithmetic

mean

of

(Xi)i=l:n,

and

the

right

hand

side of (8.19) is

the

geometric

mean

of

(Xi)i=l:n.

Answer: We first

note

that

inequality (8.19) is scalable

in

the

sense

that,

if

each variable

Xi

is multiplied by

the

same

constant

c > 0,

the

inequality (8.19)

remains

the

same. We

can

therefore assume,

without

any

loss of generality,

that

I1~=1

Xi

=

1,

and

inequality (8.19) reduces

to

proving

that

n

L

Xi

~

n,

V

Xi

>

0,

i = 1 : n,

i=l

n

with

II

Xi

=

1.

i=l

3It

can

be

shown

that

the

geometric-harmonic means inequality

1

(

IT

Yi)

n

;::::

,"",nn

1-'

V

Yi

>

0,

i = 1 : n

i=l

u~=l

Yi

follows immediately from (8.19)

by

substituting

Xi

=

t,

i = 1 : n.

(8.20)

Stefanica D. A Primer for the Mathematics of Financial Engineering

Подождите немного. Документ загружается.