Стариков А.В., Кущева И.С. Экономико-математическое и компьютерное моделирование

Подождите немного. Документ загружается.

∆

)(

Подставляя в данную формулу значения, приведенные в таблице выше,

получаем следующие величины для ценности каждой дополнительной единицы

каждого типа сырья: 1,0,2

321

YYY . Полученные результаты свидетельст-

вуют, что дополнительные вложения в первую очередь следует направлять на

закупку сырья

S и лишь затем − на закупку сырья

S .

Для ответа на четвертый вопрос опять обратимся к рис. 8. Из него видно,

что при небольшом изменении коэффициентов целевой функции

с и

с прямая

17)( =XZ вращается вокруг точки C. Таким образом, точка C будет оставаться

оптимальной до тех пор, пока прямая )(XZ не выйдет за пределы, определяе-

мые 1-м и 3-м ограничениями, т.е. пока вектор-градиент )(XZ∇ будет нахо-

диться между векторами-нормалями

A и

A к прямым, соответствующим 1-му

и 3-му ограничениям.

Определим сначала диапазон изменения коэффициента

с при фиксиро-

ванном коэффициенте

с (

с =4). Тангенсы углов наклона для векторов )(XZ∇ ,

A ,

A соответственно равны:

/)( cctg

, 1)(

tg , 2)(

tg .

Поэтому диапазон изменения коэффициента

с в целевой функции определится

из соотношения 2/1

≤

cс , т.е. 42

≤

c . Диапазон изменения коэффициента

с при фиксированном значении

с (

с=3) определяется аналогично, т.е.

≤

c .

Решение ЗЛП симплекс-методом

Симплекс-метод − универсальный метод решения ЗЛП, разработанный в

1949 г. американским математиком Дж. Данцигом. В его основе лежит идея по-

следовательного улучшения полученного решения, для реализации которого

необходимы [9]:

1) способ определения какого-либо первоначального допустимого ба-

зисного решения задачи;

2) правило перехода к лучшему (по крайней мере, не худшему) реше-

нию;

3) критерий проверки оптимальности найденного решения.

Для использования симплекс-метода ЗЛП должна быть приведена к кано-

ническому (стандартному) виду, т.е. система ограничений ее модели (за исклю-

чением тривиальных, или естественных ограничений) должна быть представле-

на в виде уравнений (равенств). Переход к канонической ЗЛП (КЗЛП) выполня-

ется следующим образом [20]:

− ограничения, представленные неравенствами, преобразуются в уравне-

ния за счет добавления фиктивных неотрицательных переменных

),( mnnkx

+= , которые одновременно входят в целевую функцию с

коэффициентом 0, т.е. не оказывают влияния на ее значение;

− переменные, на которые не наложено условие неотрицательности,

представляются в виде разности двух новых неотрицательных пере-

менных, т.е. )0,0(,

≥

−

jjjjj

xxxxx .

Ниже рассмотрен пример использования симплекс-метода для решения

задачи производственного планирования как частного случая общей задачи ли-

нейного программирования (ОЗЛП).

Пример решения задачи производственного планирования

симплекс-методом

Решим симплекс-методом задачу, математическая модель которой пред-

ставлена соотношениями (3.12) − (3.17). Прежде всего, преобразуем с помощью

дополнительных переменных неравенства (3.13) − (3.15) в уравнения. В данном

случае все дополнительные переменные (их число равно 3) вводятся со знаком

«плюс», так как рассматриваемые неравенства представляют собой неравенства

вида «меньше или равно».

Получим систему ограничений в виде:











=++

.72

521

421

321

xxx

(3.18)

Для нахождения первоначального базисного решения разобьем перемен-

ные на две группы − основные и не основные (вспомогательные). Для этого

можно воспользоваться следующим простым правилом для определения основ-

ных переменных [20]: в качестве основных переменных на первом шаге следует

выбрать (если это возможно) такие

переменных, каждая из которых вхо-

дит только в одно из

уравнений системы ограничений, при этом нет таких

уравнений, в которые не входит ни одна из этих переменных.

Введенные выше дополнительные переменные

x ,

x и

x удовлетворяют

данному требованию. Кроме того, выбранные основные переменные имеют те

же знаки, что и соответствующие им свободные члены в правых частях уравне-

ний, т.е. полученное на первом шаге базисное решение будет допустимым.

I шаг. Основные переменные:

x ,

x .

Вспомогательные переменные:

x ,

x .

В системе уравнений (3.18) выразим основные переменные через вспомо-

гательные, т.е. получим следующую систему уравнений:











−−=

.27

215

214

213

xxx

(3.19)

Приравняв вспомогательные переменные к нулю, т.е. положив 0

x и

x , получим допустимое базисное решение )7;9;5;0;0(

=X . Это решение

соответствует совпадающей с началом системы координат O (0; 0) вершине A

пятиугольника ABCDE, который представляет ОДР задачи (см. рис. 7 выше).

Проверим, не является ли полученное допустимое базисное решение оп-

тимальным. Для этого рассмотрим выражение для целевой функции

43)( xxXZ += , которое для найденного решения

X равняется значению

функции 0)(

== XZZ . Очевидно, что значение функции )(XZ можно увели-

чить путем увеличения любой из вспомогательных переменных, входящих в

выражение для

с положительным коэффициентом. Это можно осуществить,

перейдя к новому допустимому базисному решению, в котором эта переменная

будет основной, т.е. сможет принимать не нулевое, а положительное значение

(если новое решение окажется вырожденным, то целевая функция сохранит

свое значение). При таком переходе одна из основных переменных становится

вспомогательной, что в геометрической трактовке означает переход к соседней

вершине пятиугольника ABCDE, в которой значение целевой функции «лучше»

(по крайней мере «не хуже»). В данном случае для увеличения значения

можно переводить в основные переменные либо

x , либо

x , так как обе эти пе-

ременные входят в выражение для

со знаком «плюс». Выберем переменную

x , так как ее коэффициент больший, чем у

x .

Система уравнений (3.13) − (3.15) накладывает ограничения на рост пе-

ременной

x . Поскольку все переменные должны оставаться неотрицательны-

ми, выполняются следующие неравенства (при этом 0

x как вспомогательная

переменная):











≥−=

027

откуда











=≤

≤

.5,3

(3.20)

Очевидно, что сохранение условия неотрицательности всех переменных

(допустимость решения) возможно, если не нарушается ни одна из границ, по-

лученных для всех уравнений (3.20). В данном случае возможное наибольшее

значение для переменной

x определяется как 5,3}5,3;9;5min{

x . При

5,3

x основная переменная

x обращается в нуль и переходит во вспомога-

тельные. Третье уравнение системы (3.19), где достигается наибольшее воз-

можное значение переменной, переводимой в основные (т.е. где оценка мини-

мальна), называется разрешающим (подчеркнуто).

II шаг. Основные переменные:

x ,

x .

Вспомогательные переменные:

x ,

x .

Выразим новые основные переменные через новые вспомогательные пе-

ременные, начиная с разрешающего уравнения:











−−−−=

−−=

2/)7(29

2/)7(5

2/)7(

5114

5113

512

xxxx

xxx

(3.21)

или











+−=

−−=

.5,05,15,5

5,05,05,1

5,05,05,3

514

513

512

xxx

(3.22)

Второе базисное решение }0;5,5;5,1;5,3;0{

X является допустимым

и соответствует вершине B(0; 3,5) на рис. 7. Переход от решения

X к решению

X геометрически можно интерпретировать как переход от вершины А(0; 0) к

вершине B(0; 3,5) пятиугольника ABCDE.

Проверим, не является ли оптимальным полученное решение. Запишем

целевую функцию, выраженную через вспомогательные переменные, исполь-

зующиеся на данном шаге:

.1414222143

)5,05,05,3(4343)(

51511

5112122

=+−=−−+=

=−−+=+==

xxxxx

xxxxxXZZ

(3.23)

Убедимся, что полученное решение лучше, чем предыдущее (т.е. значение

увеличилось): 14014

121

−

∆

ZZZ .

Вычисленное значение )(

XZ не является максимальным, поскольку в

выражении для целевой функции (3.23) имеется переменная

x с положитель-

ным коэффициентом, равным 1. Система уравнений (3.22) накладывает ограни-

чения на рост переменной

x . Обеспечивая выполнение условия неотрицатель-

ности переменных, запишем следующие неравенства:











≥+−=

≥−−=

,05,05,15,5

05,05,05,1

05,05,05,3

514

513

512

xxx

(3.24)

откуда, полагая 0

x , получим











≤

(3.25)

Полученная система неравенств (3.25) определяет наибольшее значение

для переменной

x : 3}3/11;3;7min{

x . При 3

x переменная

x обращает-

ся в нуль, поэтому ее предполагается перевести во вспомогательные перемен-

ные. Второе уравнение системы (3.22) является разрешающим, переменная

переходит во вспомогательные переменные,

x − в основные.

III шаг. Основные переменные:

x ,

x .

Вспомогательные переменные:

x ,

x .

Как и на шаге II, выразим новые основные переменные через новые

вспомогательные переменные, начиная с разрешающего уравнения.

531

5,05,15,0 xxx

−

531

23 xxx

−

. (3.26)

Подставляем выражение для

x в следующее уравнение:

,25,05,05,15,3

5,0)23(5,05,35,05,05,3

53553

553512

xxxxx

xxxxxx

−+=−−+−=

−

532

2 xxx

−

. (3.27)

Подставляем выражение для

x в следующее уравнение:

,315,05,135,45,5

5,0)23(5,15,55,05,15,5

53553

553514

xxxxx

xxxxxx

−+=+−+−=

−

534

31 xxx

−

. (3.28)

В результате преобразований (3.26) − (3.28) получаем следующую систе-

му уравнений:











−+=

+−=

.31

534

532

531

xxx

(3.29)

Базисное решение )0;1;0;2;3(

=X соответствует вершине C(3; 2) пяти-

угольника ABCDE, представляющего ОДР задачи (см. рис. 7 выше). Выражаем

целевую функцию через вспомогательные переменные:

.217448369

)2(4)23(343)(

535353

53532133

xxxxxx

xxxxxxXZZ

−−=−+++−=

=−+++−=+==

(3.30)

Полагая 0

x и 0

x , вычислим значение целевой функции

.17)(

== XZZ Убедимся, что полученное решение лучше, чем предыдущее:

31417

232

−

∆

ZZZ , т.е. значение целевой функции возросло по сравне-

нию со значением, вычисленным на шаге II. Кроме того, третье допустимое ба-

зисное решение является оптимальным, так как коэффициенты вспомогатель-

ных переменных в выражении для целевой функции (3.30) являются отрица-

тельными, т.е. рост значений

x и

x не приведет к увеличению значения

Таким образом, оптимальным решением задачи является 3

x и 2

x ,

обеспечивающие оптимальное значение целевой функции 17),(

xxZ . С уче-

том экономического смысла рассмотренной задачи можно сделать следующий

вывод: для получения максимальной прибыли, равной 17 денежным единицам,

предприятие должно выпускать и реализовать 3 единицы продукта

P и 2 еди-

ницы продукта

P . При этом дополнительные переменные

x ,

x и

x показы-

вают разницу между запасами сырья (ресурсов) каждого вида и их потреблени-

ем, т.е. остатки ресурсов. При выполнении оптимального плана производства

xx , т.е. сырье

S и

S расходуется полностью, а остаток сырья

S равен

1 единице.

В заключение сформулируем критерий оптимальности решения при оты-

скании максимума линейной функции, а также определим возможные подходы

к отысканию минимума линейной функции.

Если при отыскании максимума линейной функции в ее выражении, со-

держащем вспомогательные переменные, отсутствуют положительные коэф-

фициенты, полученное решение оптимально.

При поиске минимума линейной функции

можно использовать сле-

дующие два пути [9]:

1) отыскать максимум функции

, полагая

−

и учитывая, что

maxmin

−

;

2) модифицировать симплекс-метод: на каждом шаге уменьшать линей-

ную функцию за счет той вспомогательной переменной, которая вхо-

дит в выражение линейной функции с отрицательным коэффициен-

том.

Глава 4.

Транспортная задача

К ЗЛП транспортного типа (кратко: транспортной задаче − ТЗ) прихо-

дят при рассмотрении различных практических ситуаций, связанных с состав-

лением наиболее экономичного плана перевозок продукции, управления запа-

сами, назначением персонала на рабочие места, оборотом наличного капитала и

многими другими.

Цель ТЗ в изначальном виде − поиск самых низкозатратных схем транс-

портировки товарных запасов или поставок от многих поставщиков (пункты

отправления) ко многим потребителям (пункты назначения). Поставщиками

могут быть фабрики, склады, отделы или другие места, из которых отправля-

ются товары. Потребителями также могут быть фабрики, склады, отделы или

любые другие места, которые получают товары.

Информация, необходимая для использования модели ТЗ, включает сле-

дующее [21]:

1. Список пунктов отправления (ПО) и пропускная способность каждого

из них или количество поставок за определенный период.

2. Список пунктов назначения (ПН) и их показатели спроса за определен-

ный период.

3. Стоимость транспортировки единицы товара из каждого пункта от-

правления в каждый пункт назначения.

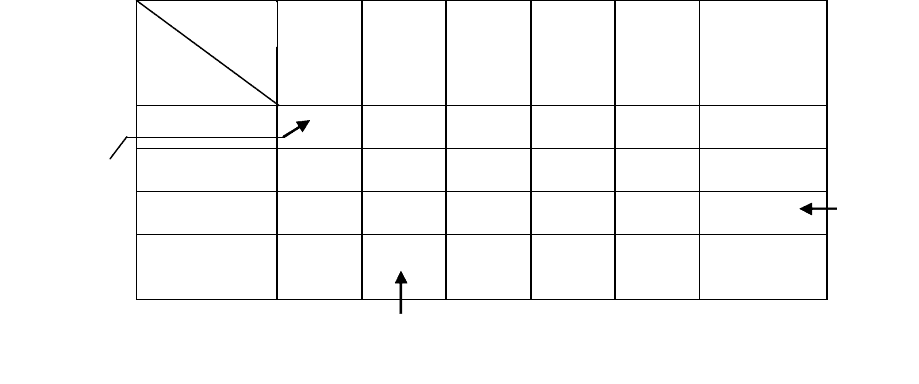
Эта информация представляется в виде так называемой транспортной табли-

цы (рис. 9).

Запасы

2 3 4 2 4 140

8 4 1 4 1 180

9 7 3 7 2 160

Потреб-

ности

60 70 120 130 100 480

ПО

ПН

Запас товара в пункте

отправления A

Стоимость транспортировки

одной единицы товара из

пункта отправления A

пункт назначения B

Потребность в товаре в

пункте назначения B

Рис. 9. Пример транспортной таблицы

Ниже рассмотрена общая постановка ТЗ и выполнено построение ее ма-

тематической модели [16].

Экономико-математическая модель ТЗ

Постановка задачи. Некоторый однородный товар (продукт, груз), нахо-

дящийся у

поставщиков

A в количестве

a единиц

)

,...,

(

необходимо

доставить

потребителям

B в количестве

b единиц

,...,

(

Известна

стоимость

c перевозки единицы товара от

-го поставщика к

-му потребите-

лю. Необходимо составить план перевозки, имеющий минимальную стоимость.

Основное предположение, используемое при построении модели, состоит в

том, что величина транспортных расходов на каждом маршруте прямо пропор-

циональна количеству единиц перевозимого товара.

Построение математической модели. Обозначим через

x количество

единиц товара, запланированных к перевозке от

-го поставщика к

-му по-

требителю. Тогда математическая модель ТЗ формулируется следующим обра-

зом:

∑∑

= =

→=

ijij

xcXZ

1 1

min)( (4.1)

при ограничениях

∑

≤

iij

)

,...,

(

; (4.2)

∑

≥

jij

)

,...,

(

; (4.3)

≥

x , (

;

,...,

). (4.4)

Ограничения (4.2) означают, что суммарный объем перевозок от

-го по-

ставщика не может превышать имеющегося у него запаса товара. Ограничения

(4.3) означают, что суммарные перевозки товара

-му потребителю должны

полностью удовлетворить его потребности в товаре. Ограничения (4.4) исклю-

чают обратные перевозки.

Из ограничений (4.2) и (4.3) следует, что

∑ ∑

= =

≥

1 1

Если имеет место равенство

∑ ∑

= =

1 1

, (4.5)

то модель называется сбалансированной транспортной моделью. В сбаланси-

рованной модели ограничения (4.2) − (4.3) имеют вид равенств. В реальных ус-

ловиях запас товара не всегда равен спросу (потребности), но транспортную

модель всегда можно сбалансировать.

В случае превышения запаса над спросом, т.е. если

∑ ∑

= =

1 1

, вводится

фиктивный

)

(

-й потребитель со спросом

∑ ∑

= =

−=

jin

bab

1 1

а соответствующие стоимости

1, +ni

)

,...,

(

считаются равными нулю.

Аналогично, при

∑ ∑

= =

1 1

вводится фиктивный

)

(

-й поставщик с

запасом товара

∑ ∑

= =

−=

ijm

aba

1 1

а соответствующие стоимости

,1+

)

,...,

(

считаются равными нулю.

Таким образом, исходная задача сводится к сбалансированной ТЗ, из оп-

тимального плана которой получается оптимальный план несбалансированной

ТЗ.

Примечание 1. Несбалансированную ТЗ называют также открытой ТЗ,

тогда как сбалансированную ТЗ − закрытой ТЗ.

Примечание 2. Стремление сбалансировать ТЗ обусловлено возможно-

стью применить в этом случае эффективный вычислительный метод.

Ниже приведен пример сбалансированной ТЗ и дано ее решение с под-

робными пояснениями [16].

Задача № 11. На трех базах (пунктах отправления)

321

,, AAA находится

однородный груз в количествах, соответственно равных 140, 180 и 160 едини-

цам. Этот груз требуется перевести в пять пунктов назначения

54321

,,,, BBBBB

соответственно в количествах 60, 70, 120, 130 и 100 единиц. Стоимости пере-

возки единицы груза из каждого пункта отправления в соответствующие пунк-

ты назначения указаны в табл. 10.