Stacey F.D., Davis P.M. Physics of the Earth
Подождите немного. Документ загружается.


//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C10.3D
–
147
– [135–148] 13.3.2008 10:35AM
(Eq. (10.27)) and rheological properties are very
sensitive to it. For materials such as minerals,
steady creep is observed only if T/T
M
is reasonably
high and at lower temperatures brittle failure
occurs instead. In the Earth the distinction is
apparent in the distribution of earthquakes,
which are restricted to relatively cool regions.
From a study of the thermal structure of the litho-
sphere at the point of subduction, McKenzie et al.
(2005) reached the conclusion that earthquakes
occur only where the temperature is below
600 8C. They interpreted this as the temperature
distinguishing brittle failure from creep. From
a detailed study of Californian earthquakes,
Bonner et al. (2003) concluded that the limit is
nearer to 400 8C. Taking the solidus temperature
of the uppermost mantle as T
M
1400 K, we can
refer to a homologous temperature, T/T
M
¼0.5
to 0.6, as the critical condition distinguishing
seismic from aseismic behaviour. Although T
M
is not well defined, because the different miner-
als have different melting points, we take this
condition as an approximate guide to the varia-
tion in homologous temperature throughout
the mantle. T/T
M
< 0.5 only near to the surface
and in subducting slabs in the upper mantle
and not at all in the lower mantle. Implications
for lower mantle temperatures are considered in
Section 19.5.
10.7 Frequency dependent
elasticity and the dispersion
of body waves
Consider the special case of a seismic pulse
that starts as a function, a square pulse of
infinitesimal duration. Its Fourier spectrum is
initially white, that is, wave components of all
frequencies have the same energy per unit fre-
quency interval. Crests of all of the component
waves coincide at the initiating function, but
cancel elsewhere. But this cancellation fails
as soon as the mix of components changes by
selective removal of high frequencies. If we
make the assumption that all frequencies
travel at the same speed, then the coinciding
crests stay together as a peak of the pulse. But
it does not remain as a sharp function; it
spreads out symmetrically to both earlier and
later times. The peak would arrive at any point
down the path at the time expected from the
wave speed, so half of the pulse arrives faster
than the wave speed. Worse, since there is no
sharp onset of the pulse, it begins to arrive
even before it has been initiated. This viola-
tion of the principle of causality demonstrates
that there is an erroneous assumption: wave
components of different frequencies cannot
travel at the same speed. A frequency-dependent
attenuation coefficient necessarily implies also
frequency-dependent speed or wave dispersion.
In the special case of frequency independent
attenuation, that is Q / !, there would be no
dispersion because all harmonic components of
a pulse would be similarly attenuated and it
would propagate undeformed, but with dimini-
shing amplitude.
The problem of attenuation-related disper-
sion is discussed by Aki and Richards (2002) and
the mathematical theory, based on the require-
ment of causality, is reviewed by Brennan and
Smylie (1981). Most discussions emphasize the
approximation of constant Q, that is Q independ-
ent of frequency, which yields a relationship
between the phase speeds, v, at two frequencies
and the Q of the medium,
vðf
1
Þ
vðf
2
Þ
¼ 1 þ
1
pQ
ln
f
1
f
2
: (10:29)
This is a valuable result, showing that, for values
of Q observed for the Earth, the dispersion is
slight but not insignificant over the frequency
range of seismology. It is much more important
in comparing observations at seismic frequen-
cies with laboratory measurements at MHz or
GHz frequencies. In any case, Eq. (10.29) assumes
constant Q, and so is only a rough approximation
to the real Earth situation.
A more general treatment requires solution
of an integral involving the attenuation coeffi-
cient ( in Eq. (10.20)). The variation in phase
speed, v, with frequency, !
0
/2p, can be obtained
for an arbitrary variation of with frequency,
using alternative expressions that relate v to
speed c at infinite frequency (Brennan and
Smylie, 1981),
10.7 FREQUENCY DEPENDENCE AND DISPERSION 147

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C10.3D
–
148
– [135–148] 13.3.2008 10:35AM
1
vð!
0
Þ
¼
1
c
1
p!
0
pv
ð
1
1
ð!Þ
!
0
!
d!
¼
1
c
2
p
pv
ð
1
0
ð!Þ
!
2
0
!
2
d!; (10:30)
where pv indicates the Cauchy principal value of
the integral and care is required in handling the
singularities. The first version of this integral is
the Hilbert transform of (!). Provided (!)is
known over a range extending well beyond the
frequency range of immediate interest, the
high-frequency limits of the integrals present
no problem because we are interested only in
the differences in v between finite values of !
0
and so subtract integrals from one another. A
simple qualitative argument shows what result
to expect. If is independent of !, corresponding
to Q / ! or f, then the integrals in Eq. (10.30) are
independent of !
0
and there is no dispersion. In
this case we can see that all of the Fourier com-
ponents of the function pulse considered above
are similarly attenuated. The pulse propagates
with diminishing amplitude but no change in
shape and no dispersion.
Now we can apply a simple amendment to
Eq. (10.29) to allow for frequency dependent Q.
If we write
Q / f
"
(10:31)
and consider an average of Q
1
over a moderate
frequency range of interest, then the equation
vðf
1
Þ
vðf
2
Þ
1 þ
ð1 "Þ
p
ln
f
1
f
2
hQ
1
i (10:32)
satisfies the two conditions, " ¼0 (Eq. (10.29)) and
" ¼1 (no dispersion). Equation (10.32) agrees with
laboratory data on diverse materials, including
plastics, metals, minerals and rocks, but it is
an empirical approximation, justified by the
fact that it is intermediate between the exact
solutions of Eq. (10.30) for " ¼0and" ¼1. Over
the frequency range from body waves to free
oscillations of the Earth, " 1/3 appears to be a
reasonable approximation, so that dispersion is
only about 2/3 as strong as in Eq. (10.29).
Linear anelastic mechanisms are relaxation
phenomena, so that, after a disturbance to any
element of material, causing an immediate elastic
response, there is a further, delayed, anelastic
response, which is an exponential relaxation
towards an equilibrium state. Thermally activated
movements of crystal dislocations past potential
barriers and the redistribution of heat between
compressed or dilated crystals with different
thermodynamic properties are examples of pro-
cesses that cause such relaxation. It follows
that the elastic modulus has a higher value at
high frequencies, which do not allow time for
the relaxation to occur, than at lower frequencies.
These are causes of a difference between relaxed
and unrelaxed moduli, considered in the special
case of composite materials in Section 10.4.
The variation of elastic modulus with fre-
quency is twice as strong as the variation in
phase speed, which depends upon the square
root of elastic modulus. In some analyses what
is here referred to as the elastic modulus is con-
sidered to be the real part of a complex modulus,
with the imaginary part representing strain that
is p/2 out of phase with stress. The real compo-
nent, or modulus, is the gradient of the axis of a
hysteresis loop, as in Fig. 10.3, and experiments
confirm that the modulus increases with fre-
quency. If the phase lag between strain and
stress is then Q
1
¼tan , which is the ratio
of imaginary t o real components of t he modulus
(not to be confused with the logarithmic decre-
ment (Eq. (10.21)).
Since body waves have a slight positive dis-
persion (phase speed increasing with frequency),
group speed is slightly greater than phase speed
(see Eqs. (16.49) to (16.51)). Thus, at any particu-
lar frequency,
u ¼ v= 1
1 "
pQ
: (10:33)
However, u is less than the limiting phase speed
at high frequency, which corresponds to the
value of v for the completely unrelaxed modulus.
It should be emphasized that the theory of
body wave dispersion is valid only for linear
attenuation mechanisms that operate at large dis-
tances from earthquakes. As we have mentioned,
anelasticity may be non-linear within about
ten fault dimensions. We have referred also to
the observational problem that high frequency
waves are more readily scattered than low fre-
quencies and effects of scattering can be confused
with attenuation.
148 ELASTIC AND INELASTIC PROPERTIES
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D
–
149
– [149–162] 13.3.2008 11:19AM
11
Deformation of the crust: rock mechanics
11.1 Preamble
The theory of elasticity in Chapter 10, even the
discussion of inelastic deformation, does not pro-
vide a description of the processes that led to the
geological features that we see in the surface
layers of the crust. We need a different theoretical
approach to the deformation of materials such as
crustal rocks that are granular, cool and at low
pressure. What determines how or why rocks
deform or break? How are the orientations of
faults related to the stresses that cause them?
How is crustal stress estimated? How is the safety
of mines and tunnels assessed? Can laboratory
observations of rock failure be extrapolated to
describe earthquakes? These are questions
addressed by the discipline of rock mechanics.
In its modern form it is used mainly by mining
engineers and the applied mathematicians who
work with them. Here it is applied to tectonics.
The mathematical methodology of the sub-
ject uses the tensor notation. This is given a
brief introduction in Section 10.3, in the discus-
sion of elasticity of crystals, and is extended in
this chapter. It is a convenient representation of
stress patterns involving superimposed com-
pression and shear, including rotation of refer-
ence axes, to identify principal stresses. The
most obvious and useful application is to the
criteria for mechanical failure.
Earthquakes are dramatic instances of failure
and most of them are shallow, by which we mean
that they are confined to the lithosphere, the cool
surface layer of the Earth. The exceptions occur in
the zones of subduction or convective downwel-
ling, where planes of earthquake foci trace the
penetration of the mantle by the cool lithospheric
material to depths as great as 700 km. They are
examples of mechanical failure, in which material
loses its coherence. It is essentially a phenomenon
of ‘cool’ material, at homologous temperatures
T/T
M
< 0.5, where T
M
is the melting point or
solidus temperature. Most of the mantle is at
higher temperatures and its convective defor-
mation, described as creep in Section 10.6,
occurs without sudden, localized failure.
Rock mechanics provides an interpretation of
different styles of faulting in terms of stress ori-
entations in the remote past as well as now.
Earthquake fault plane solutions (Section 14.4)
give the same information much more widely,
but only at the present time. Stresses in aseismic
areas are determined by application of rock
mechanics equations to borehole measure-
ments. All of these observations are combined
to produce stress maps, which now cover a large
fraction of the globe.
11.2 The tensor representation
of stress and strain
Stress can be represented in three dimensions as
a tensor. We consider an orthogonal coordinate
system (x
1
,x
2
,x
3
), written x
i
, being the Cartesian
(x,y,z), and identify three areas each with its nor-
mal aligned with one of the axes. Each area is
represented by a unit vector n
i
in the direction of

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D
–
150
– [149–162] 13.3.2008 11:19AM
the normal and a magnitude A
i
. In the conven-
tion of continuum mechanics, stress is the force
per unit area exerted on material on the negative
side of the area by material on the positive side.
An area can be subjected to three independent
forces, one normal to it (in the direction of n
i
),
and two tangential. With three force compo-
nents acting on each of the three areas, a total
of nine stress components is possible. However,
as we shall see, only six are independent. A nor-
mal stress is a force, parallel to the area normal,
divided by the area on which it acts. It can be
either extensional or compressional depending
on whether the force is directed parallel or anti-
parallel to the area normal. In this convention an
extensional stress is positive but the opposite sign
convention is used in rock mechanics, in which
compressions predominate. The convention that
compression is positive is also used in treatments
of finite strain and high pressure equations of
state (Chapter 18). Recognizing the danger of con-
fusion, we use the continuum mechanics conven-
tion where this is standard and convert to the
rock mechanics convention for the discussion of
the Mohr circle in Section 11.4 and crustal
stresses in the following sections.
Shear stresses are the tangential forces per
unit area. A component of the stress tensor,
written
ij
, corr esponds to a f orce acting in
direction i on unit area of a plane with normal
j. Shear stress is positive if the force acts in the
positive i direction on t he positive side of the j
plane. With the corresponding Cartesian
notation,
ij
¼
11
12
13
21
22
23
31
32
33
2
6
4
3
7
5
¼
xx
xy
xz
yx
yy
yz
zx
zy
zz
2
6
4
3
7
5
: ð11:1Þ
In one dimension, strain is a fractional
change in length. In three dimensions, six
strains are possible, three length changes, in
the x
1
, x
2
and x
3
directions, denoted e
11
, e
22
, e
33
,
and three shears e
12
, e
23
, e
13
. The shear strain is
defined as half the angular change in the right
angle defined in the material by the x
i
, x
j
axes
prior to deformation. From this it is evident that
e
ij
¼e
ji
, and that there are only three independent
shear strains. This is mentioned in Section 10.3
and explained again below.
After application of a stress, the new positions
of material points in a body are given by the
displacement field u(x,y,z). Strains are gradients
in the displacement field. Consider a body sub-
jected to a stress that causes a displacement defor-
mation field u ¼(u
1
,u
2
,u
3
). Let the displacement in
the x
1
direction at two points a distance dx
1
apart
be u
1
and u
1
þdu
1
(Fig. 11.1). From a Taylor expan-
sion, u
1
ðx
1
þ dx
1
Þ¼u
1
ðx
1
Þþð@u
1
=@x
1
Þdx
1
þ
...
,
we retain only linear terms du
1
¼ð@u
1
=@x
1
Þdx
1
,
that is we consider only linear or infinitesimal
elasticity theory, applicable to small strains. The
strain e
11
is the change in length, (qu
1
/@x
1
)dx
1
,per
unit original length dx
1
,thatis
e
11
¼ @u
1
=@x
1
: (11:2)
We treat shear strains in a similar manner.
Figure 11.2 shows the angle changes to what
are right angles in unstrained material. Shear
strain is
e
12
¼ 1=2ð
1
þ
2
Þ¼1=2ð@u
2
=@x
1
þ @u
1
=@x
2
Þ: ð11:3Þ
If
1
6¼
2
the body rotates, with rotation defined
as ð
1
2
Þ=2 ¼
1
2
@u
2
@x
1
@u
1
@x
2
.
We can generalize these results to three
dimensions,
e
ij
¼
1
2
@u
i
@x
j
þ
@u
j
@x
i
; (11:4)
where i and j take on the values 1, 2 and 3.
Consider the volume dx
1
dx
2
dx
3
(Fig. 11.3), sub-
jected to shear stresses in the x
1
x
2
plane. The
tangential forces acting on each side from the
material external to the volume are
21
dx
2
dx
3
,
21
dx
2
dx
3
,
12
dx
1
dx
3
and
12
dx
1
dx
3
. Then
the torque is
12
dx
1
dx
3
.dx
2
21
dx
2
dx
3
.dx
1
¼
(
12
21
)dx
1
dx
2
dx
3
. For the torque to be
u
1
x
1
x
1
u
1
+
δu
1
x
1
+
dx
1
FIGURE 11.1 Variation of displacement u
1
in the
direction x
1
, giving the strain e
11
.
150 DEFORMATION OF THE CRUST: ROCK MECHANICS
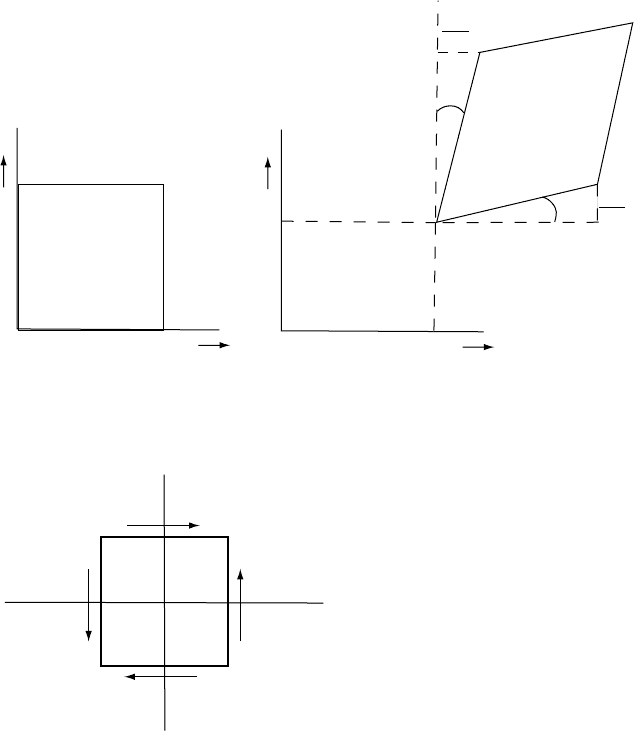
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D
–
151
– [149–162] 13.3.2008 11:19AM
independent of volume, dx
1
dx
2
dx
3
,
12
¼
21
.
Similarly
23
¼
32
and
13
¼
31
. Generalizing,
ij
¼
ji
,and,becauseinisotropicmaterialshear
stress is proportional to the corresponding strain,
e
ij
¼e
ji
, with the result that only six elements of
the stress (strain) tensor are independent.
11.3 Hooke’s law in three
dimensions
For an isotropic material two independent mo-
duli are required and there are several ways of
choosing them (Sections 10.1 and 10.2). In
most geophysics these are bulk modulus, K, relat-
ing pressure to volume change, and rigidity mod-
ulus, , relating shear stress to change of shape
with constant volume. A different choice arises
from the tensor notation in which the three
dimensional version of Hooke’s law is expressed as
11
¼ lðe
11
þ e
22
þ e
33
Þþ2e
11
;
22
¼ lðe
11
þ e
22
þ e
33
Þþ2e
22
;
33
¼ lðe
11
þ e
22
þ e
33
Þþ2e
33
;
12
¼ 2e
12
;
13
¼ 2e
13
;
23
¼ 2e
23
;
(11:5)
where l and are referred to as the Lam
´
e coef-
ficients but is familiar as the shear modulus.
Equations (11.5) can be written in a convenient
shorthand as
ij
¼ le
ij
þ 2e
ij
; (11:6)
where is the Kroeneker delta for which
ij
¼1if i ¼ j;
ij
¼0if i 6¼ j:
(11:7)
e ¼e
11
þe
22
þe
33
is the sum of fractional changes
in length in three directions which gives the rel-
ative volume change. The relationships to the
alternative isotropic moduli are here re-derived
by application of Eq. (11.6). Pressure is defined as
the average normal stress
x
1
x
2
u
1
, u
2
θ
2
θ
1
u
1
=
0, u
2
=
0
u
1
u
2
dx
1
dx
2
x
1
x
2
A
B
CD
A'
B'
C'
D'
∂u
1
dx
2
∂x
2
∂u
2
dx
1
∂x
1
FIGURE 11.2 Displacements due to shear strain. Strains involve variations in displacements as a function of the
coordinate system.
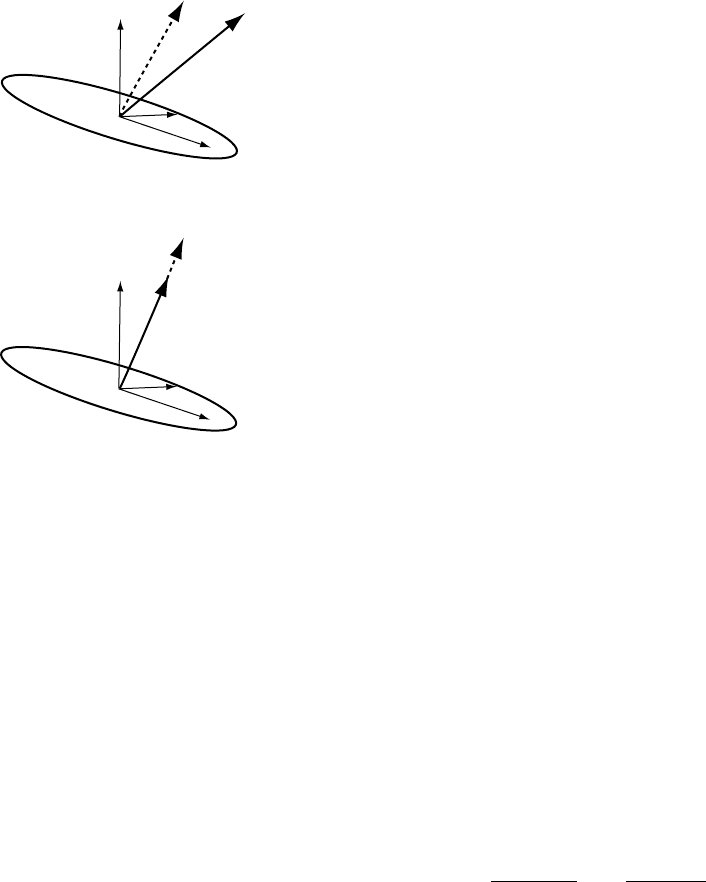
σ
12
dx
1
dx
3
σ
21
dx
2
dx
3
–
σ
12
dx
1
dx
3
–
σ
21
dx
2
dx
3
x
2
x
1
FIGURE 11.3 Forces on the faces of an elementary
volume from a stress field
ij
.
11.3 HOOKE’S LAW IN THREE DIMENSIONS 151
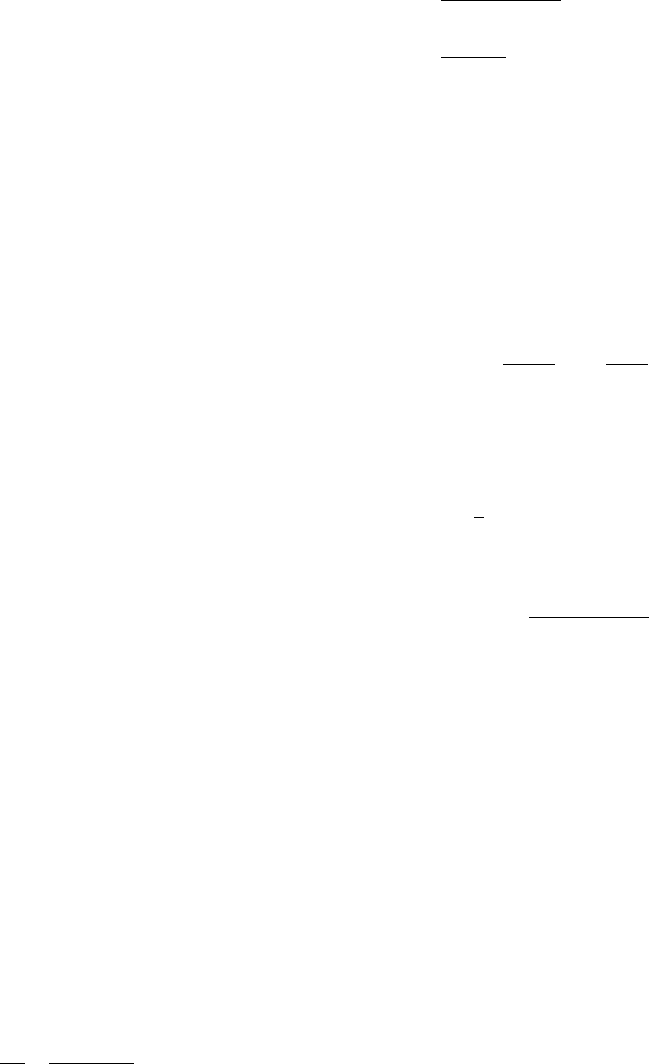
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D
–
152
– [149–162] 13.3.2008 11:19AM
p ¼P ¼ð
11
þ
22
þ
33
Þ=3; (11:8)
where P has compression positive, as used in
rock mechanics and interior stresses in the
Earth. Bulk modulus, K, the ratio of pressure to
volume change, is obtained by summing the first
three of Eqs. (11.5):
K ¼ P=e ¼ðl þ 2=3 Þ: (11:9)
Poisson’s ratio, , is not strictly a modulus, but
a dimensionless ratio. However, it is a useful
parameter that is always listed with elastic mod-
uli. Let uniaxial stress
11
be applied in the x
1
direction to a rectangular block of elastic material
with the other sides free so that the other two
stress components are zero. The block expands
laterally if the body is compressed axially or will
contract laterally if it is extended. Poisson’s ratio
is the negative ratio of lateral to longitudinal
strains (a negative sign because the strains are of
opposite signs). Equations (11.5) become
11
¼ðl þ 2Þe
11
þ le
22
þ le
33
;
0 ¼le
11
þðl þ 2Þe
22
þ le
33
;
0 ¼le
11
þ le
22
þðl þ 2Þe
33
:
(11:10)
By symmetry, the lateral strains are equal, e
22
¼e
33
,
and Poisson’s ratio is
¼e
22
=e
11
¼ l=ð2l þ 2Þ: (11:11)
An approximation that is sometimes used to
simplify rock mechanics equations is l ¼, giv-
ing ¼1/4, referred to as a Poisson solid. While
the simplification may be justified where rough
solutions suffice, it underestimates Poisson’s
ratio for most solid materials, for which ¼0.3
is a better approximation at low pressure, and it
increases systematically with pressure (for a rea-
son discussed in Section 18.8). For a fluid, ¼0,
so that by Eq. (11.11) Poisson’s ratio is 0.5 and
this applies to the outer core and oceans.
Young’s modulus, E, is the ratio of longitudi-
nal stress to strain, with no lateral stress,
22
¼
33
¼0, as in the consideration of Poisson’s ratio
in Eq. (11.11).
E ¼
11
e
11
¼
ð3l þ 2Þ
l þ
: (11:12)
We can use Eqs. (11.11) and (11.12) to solve for the
Lam
´
e coefficients, l and , in terms of Young’s
modulus and Poisson’s ratio:
l ¼
E
ð1 þ Þð1 2Þ
;
¼
E
2ð1 þ Þ
:
(11:13)
If a linear stress
11
produces a strain e
11
with
lateral strain prevented, then the first of
Eqs. (11.5) gives
¼
11
=e
11
¼ðl þ 2Þ: (11:14)
This is the modulus controlling P-wave propaga-
tion in the Earth because the juxtaposition of
compressed and extended layers ensures that
e
22
¼e
33
¼0. The lateral stresses
22
¼
33
¼
l
l þ 2
11
¼
1
11
(11:15)
are self-adjusted to make this so. A more useful
and familiar relationship for is obtained by
substituting for l by Eq. (11.9):
¼ K þ
4
3
; (11:16)
and we note that
¼ðl þ 2Þ¼
ð1 ÞE
ð1 þ Þð1 2Þ
: (11:17)
These relationships are summarized in
Appendix D.
11.4 Tractions, principal stresses
and rotation of axes
The stress tensor can be thought of as a table of
coefficients that can be multiplied by an area
vector to give the forces on that area. Consider
an element of area of size A (Fig. 11.4) with direc-
tion cosines n
j
. The forces per unit area applied to
the material on the negative side of A by material
on the positive side are called the tractions and
are given by
T
i
¼
X
3
j¼1
ij
n
j
¼
ij
n
j
(11:18)
using the Einstein summation rule for repeated
indices.
152 DEFORMATION OF THE CRUST: ROCK MECHANICS
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D
–
153
– [149–162] 13.3.2008 11:19AM
Thus
T
1
¼
11
n
1
þ
12
n
2
þ
13
n
3
;
T
2
¼
21
n
1
þ
22
n
2
þ
23
n
3
;
T
3
¼
31
n
1
þ
32
n
2
þ
33
n
3
:
(11:19)
For any stress field,
ij
,inanisotropicmaterial
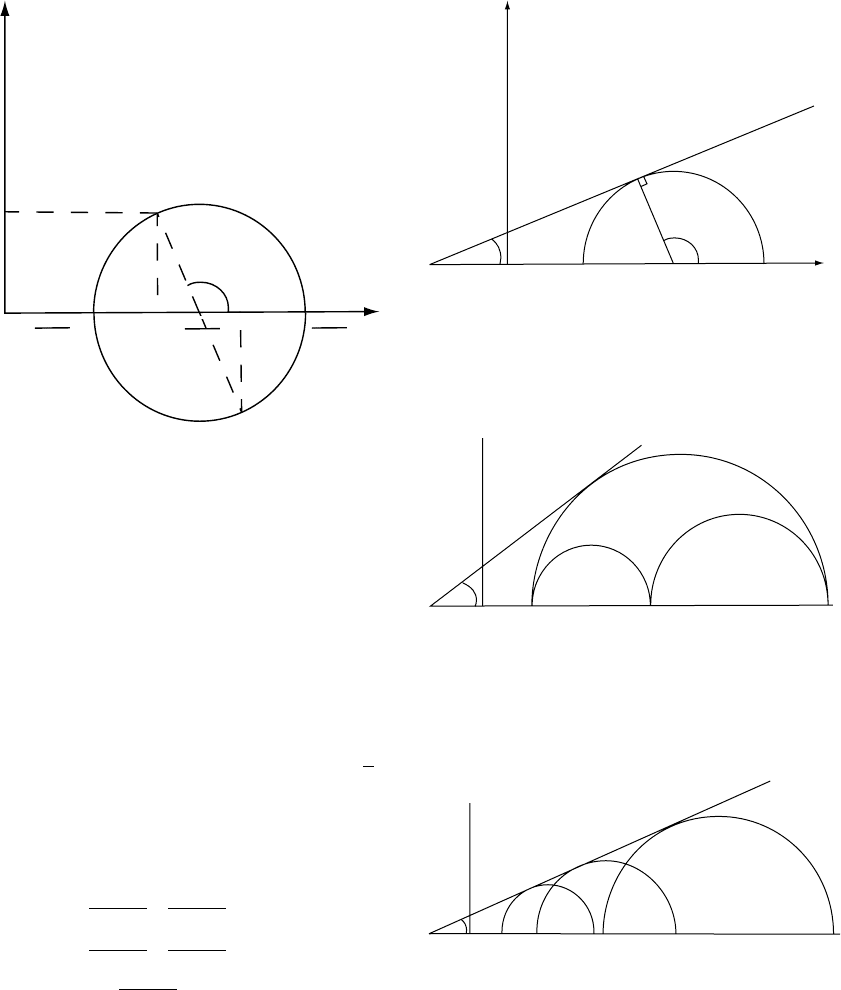
it is possible to find three orthogonal unit areas
across which the tractions have no tangential com-
ponents, that is vector T is parallel to the area
vector n (Fig. 11.4(b)), which means that n is a
direction of principal stress. This requires the trac-
tion components to be proportional to the direc-
tion cosines of the areas. Let the constant
of proportionality be l, T
i
¼ln
i
. Substituting
Eq. (11.19) for T
i
in Eq. (11.18) and using the
Einstein summation rule, with the Kroenecker
ij
,
as in Eq. (11.7),
ij
n
j
¼ l
ij
n
j
;
or
ij
n
j
l
ij
n
j
¼ 0:
To have a solution to this set of simultaneous
equations the determinant must be zero,
detð
ij
l
ij
Þ¼
ij
l
ij
¼ 0: (11:20)
Equation (11.20) is the characteristic equation
for an eigenvalue problem. In three dimensions
it is cubic in l,
xx
l
xy
xz
yx
yy
l
yz
zx
zy
zz
l
¼ 0; (11:21)
which has three roots {l
1
, l
2
, l
3
}, corresponding to
the three principal stresses. The corresponding
eigenvectors are the three unit (vector) areas
corresponding to each of l
1
, l
2
, l
3
.
To find the eigenvector corresponding to l
1
,
for example, we require three equations in three
unknowns {n
i
}. Equation (11.21) comprises two
independent equations. The third is the ortho-
normal property of the unit area vectors
P
3
i¼1
n
2
i
¼ 1. Thus for l
1
the equations are
n
2
1
þ n
2
2
þ n
2
3
¼ 1;
11
n
1
þ
12
n
2
þ
13
n
3
¼ l
1
n
1
;
21
n
1
þ
22
n
2
þ
23
n
3
¼ l
1
n
2
:
(11:22)
An example in two dimensions
In two dimensions Eq. (11.22) reduces to
ð
11
lÞ
12
12
ð
22
lÞ
¼ 0:
The characteristic equation becomes
ð
11
lÞð
22
lÞ
2
12
¼ 0;
l
2
lð
11
þ
22
Þþ
11
22
2
12
¼ 0;
(11:23)
the solution of which is
l ¼
ð
11
þ
22
Þ
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
11
22
Þ
2
2
þ
2
12
s
: (11:24)
Suppose that the stress field is a pure shear (
11
¼
22
¼0). Then l ¼
12
.
Choose l
1
¼þ
12
. Solving for the eigen-
vector,
n
2
1
þ n
2
2
¼ 1;
12
n
2
¼ l
1
n
1
;
giving n
2
¼ n
1
; and therefore
n
1
¼ n
2
¼ 1=
ffiffiffi
2
p
:
Traction
T
3
T
2
T
1
T
3
T
2
T
1
Traction
Area
(b)
Area
(a)
FIGURE 11.4 Tractions are forces applied by material
on the positive side of an elementary area under stress.
Case (a) is the general one and if the vector sum of the
tractions is normal to the area, as in case (b), then the
normal is a direction of principal stress.
11.4 ROTATION OF THE STRESS TENSOR 153

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D
–
154
– [149–162] 13.3.2008 11:19AM
As is obvious in this simple case the principal
stresses are a tension and compression equal to
the value of the shear stress and oriented at 458
to the shear direction.
Rotation of stress or strain tensors
Suppose that we wish to determine the compo-
nents of the stress tensor in a rotated coordinate
system x
0
i
relative to an unrotated system x
i
. The
traction force vector in the rotated system is
given by Eq. (11.19). The force components
resolved normal and tangential to the axial
planes of the rotated system give the new normal
and shear stresses, respectively. For example, in
two dimensions, if the axes are rotated anticlock-
wise by , the direction cosines of the area with
normal x
0
i
are n
j
¼½cos ; sin . From Eq. (11.19)
the tractions are T
1
¼ð
11
cos þ
12
sin Þ;
T
2
¼ð
21
cos þ
22
sin Þ. Stresses in the rotated
system,
0
11
and
0
12
, are found by resolving
the traction vector normal and parallel to the
area:
0
11
¼ðT
1
cos þ T
2
sin Þ;
0
12
¼ðT
1
sin þ T
2
cos Þ:
(11:25)
Inserting T
1
and T
2
we obtain
0
11
¼
11
cos
2
þ
22
sin
2
þ
12
sin 2;
0
12
¼
22
11
2
sin 2 þ
12
cos 2:
(11:26)
Repeating for the area with normal x
0
2
, i.e.,
!
p
2
þ ;
0
22
¼
11
sin
2
þ
22
cos
2
12
sin 2:
(11:27)
By examining (11.26) and (11.27) we see that the
procedure for finding tractions in the rotated
system, then resolving them to normal and tan-
gential directions to find the stresses, can be
expressed in matrix form as the product of two
rotations,
R
1
¼
cos sin
sin cos
; R
2
¼
cos sin
sin cos
:
(11:28)
Then
0
¼R
1
R
2
¼R R
T
, where T refers to the
transpose of a matrix.
Generalizing to three dimensions, we let R
ij
¼
cos(angle between x
i
and x
0
j
):
0
ij
¼
X
3
m¼1
X
3
n¼1
R
im
mn
R
nj
¼ RR
T
: (11:29)
The Mohr Circle
Consider a special case with the x
i
coordinate axes
so chosen that
12
¼
xy
¼0, that is
11
and
22
are
principal stresses, which we will denote by
1
and
2
. After rotation by angle , Eqs. (11.26) and
(11.27) may be rewritten as
0
11
0
12
0
21
0
22
¼
1
þ
2
2
r cosð2Þ r sinð2Þ
r sinð2Þ
1
þ
2
2
þ r cosð2Þ
2
6
4
3
7
5
;
(11:30)
where
r ¼
2
1
2
: (11:31)
From Eq. (11.30) we see that the normal and
shear stresses can be represented by a circle dia-
gram (Fig. 11.5). The axes of the diagram are the
normal stress and shear stress components
(
n
, ). The centre of the circle is located at
n
¼
1
þ
2
2
; ¼ 0. The radius of the circle is r
(Eq. (11.31)). The stresses in a plane with its nor-
mal at angle to the direction of the x
1
axis are
found by drawing the vector r from the point
1
þ
2
2
; 0
at angle 2 to the
n
axis. The
axis component gives the shear in the rotated
system; the
n
axis component gives one normal
stress; the
n
axis component of negative r gives
the other normal stress.
To convert the circle diagram (Fig. 11.5) from
the elastic (compressions negative ) to the rock
mechanics convention (compressions positive)
the normal stresses must be reversed in sign.
We rotate the circle diagram about the vertical
axis, and change the sign of r in Eq. (11.31) to
r ¼
1
2
2
(see Fig 11.6(a)). Then
1
is the largest
(positive) compressive stress. The circle so
formed is called the Mohr circle (Fig. 11.6(a))
154 DEFORMATION OF THE CRUST: ROCK MECHANICS
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D
–
155
– [149–162] 13.3.2008 11:19AM
after its inventor, O. Mohr. The intercepts of the
Mohr circle with the horizontal axis are the prin-
cipal stresses
1
,
2
. When the reference plane
rotates by an angle in physical space, the cor-
responding point in the Mohr circle diagram
(Fig. 11.6(a)) moves around the circle by an
angle 2. From the Mohr circle we observe
that the maximum shear occurs at 2 ¼
p
2
,or
¼458, to the principal stress direction, and
has a value equal to half the difference in mag-
nitude of the maximum and minimum principal
stresses. From Eq. (11.30) we have
0
xx
¼
1
þ
2
2
þ
1
2
2
cosð2Þ;
0
yy
¼
1
þ
2
2
1
2
2
cosð2Þ;
0
xy
¼ ¼
2
1
2
sinð2Þ;
(11:32)
from which we can derive the relation
0
xx
0
yy
¼ð
1
2
Þcosð2Þ (11:33)
which we use in Chapter 13.
The three-dimensional case involves three
principal stresses,
1
,
2
,
3
. Let
1
>
2
>
3
.We
can apply the Mohr circle analysis on each plane
containing two of the principal stresses, i.e.,
{
1
,
2
}, {
1
,
3
}, {
2
,
3
}, which results in three
Mohr circles as in Fig. 11.6(b). Then each circle
τ
r
σ
n
2
–
r
2
σ
11
+
σ
22
+
r
–r
2θ
σ'
σ'
σ'
2
σ
11
+
σ
22
σ
11
+
σ
22
11
22
12
FIGURE 11.5 Shear stress (vertical axis) plotted against
normal stresses (horizontal axis). Shear stress in a plane
at any angle to the x-axis is obtained by the projection of
the r vector on the vertical axis. Normal stresses are
obtained by the projections of the r vector and negative r
vector on the horizontal axis.
φ
σ
2
σ
1
σ
n
τ
r
2θ
S
o
FIGURE 11.6(a) Mohr circle. Special case where the
horizontal axis is the direction of greatest principal
stress. The sloping line gives the frictional strength.
Frictional failure occurs when the Mohr circle intersects
the friction line.
φ
τ
σ
3
σ
2
σ
1
σ
n
S
o
FIGURE 11.6(b) Mohr circle for three dimensions. Each
circle represents a plane containing two of the principal
stresses. The failure line occurs in the plane with the
greatest shear stress.
φ
σ
n
τ
S
o
FIGURE 11.6(c) Increasing pressure causes stability
against frictional failure by moving the centres of Mohr
circles to the right, which means greater shears must be
developed for their radii to reach the failure line.
11.4 ROTATION OF THE STRESS TENSOR 155
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C11.3D
–
156
– [149–162] 13.3.2008 11:19AM
describes stress components on a plane lying
between the principal stress pair. We see that
in Fig. 11.6(b) the maximum shear occurs in the
plane containing the intermediate principal
stress and bisects the angle between the greatest
and least principal stresses.
11.5 Crustal stress and faulting
Since any stress pattern can be resolved into three
principal stresses,
1
,
2
,
3
, and deep in the Earth
these are all large compared with the differences
between them, it is often convenient to identify the
average as a hydrostatic pressure, as in Eq. (11.8),
recalling that p ¼(
1
þ
2
þ
3
)/3, and we refer to
the differences as deviatoric stresses. These are
generally small enough to be treated by the linear
(infinitesimal) elasticity theory, allowing a simple
superposition on hydrostatic compression, even
when the response to hydrostatic pressure is
strong enough to require analysis by a finite strain
theory, as in Chapter 18. Except near to the sur-
face, the hydrostatic pressure, P, is approximated
by the lithostatic or overburden pressure,
P
ð
z
0
g dz; (11:34)
which can be used as one of the equations needed
for complete specification of the stress pattern. In
common usage this is a positive quantity, but for
substitution in the standard equations of elastic-
ity theory, in which extension is positive, pres-
sure is taken as the negative quantity P.Then
the tectonic stresses causing deformation, the
deviatoric stresses, are obtained from the total
stresses by subtracting the pressure, p:
ij
¼
ij
p
ij
¼
ij
þ P
ij
: (11:35)
Faults are often planes of weakness estab-
lished by repeated movements, but their original
causes were tectonic stresses in directions that
determined the fault orientations. Tectonic
movements, ultimately driven by mantle con-
vection, persist in the same directions for many
millions of years, so that faults reflect the driving
forces that caused them, even where established
planes of weakness may now have a strong influ-
ence. Similarly, faults that are no longer active
indicate the orientations of stresses that moved
them many years ago. This is the reason for
interest in the classification of faults. They are
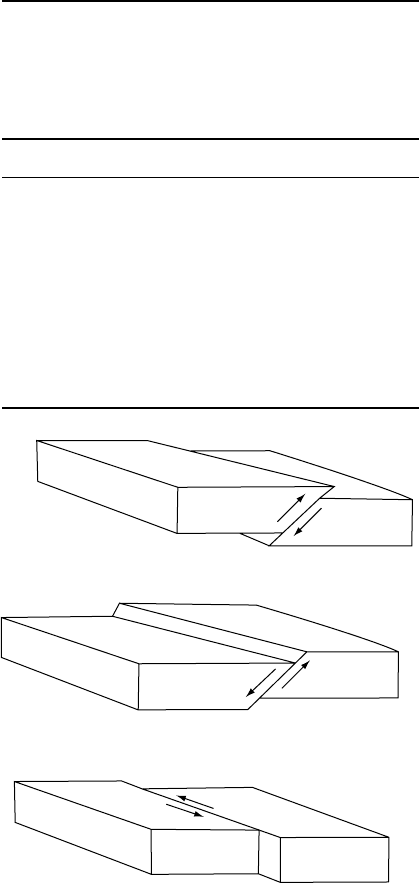
of three types, illustrated in Fig. 11.7, corres-
ponding to different stress orientations, as clas-
sified by Anderson (1905). The Anderson faulting
criteria are summarized in Table 11.1.
Reverse fault
Normal fault
Strike-slip fault
FIGURE 11.7 Different fault types.
Table 11.1 Anderson faulting criteria.
1
,
2
,
3
, are maximum, intermediate and
minimum principal stresses, respectively.
Note that ‘strike’ means the orientation of
the surface trace of the fault
1
2
3
Normal
fault
vertical horizontal
along
strike
horizontal
Strike slip
fault
horizontal
(angle to
strike)
vertical horizontal
Reverse
(thrust)
fault
horizontal horizontal
along
strike
vertical
156 DEFORMATION OF THE CRUST: ROCK MECHANICS
