Смирнова Е., Чупахина Е. Учебно-методический комплекс по курсу Прогнозирование и планирование развития АПК

Подождите немного. Документ загружается.

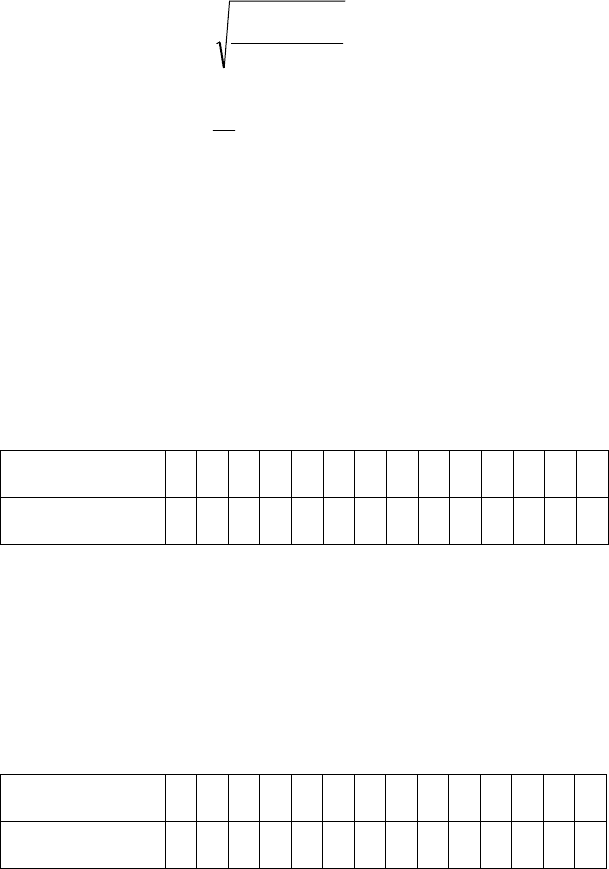
171

5. Среднеквадратическое отклонение рассчитывается

по формуле:

ХХ

∑

−

)(

Коэффициент вариации рассчитывается по формуле:

%100⋅=

Медиана ранжированного ряда - это значение призна-

ка, которая находится в середине ранжированного ряда.

Для нахождения медианы с четным числом экспертов скла-

дываются два средних значения середины ранжированного

ряда, и эта сумма делится пополам.

Решение:

Первый тур опроса

Таблица 9 - Результаты первого тура экспертизы

Экспертные

данные

Ранжированный

ряд

Х =

Медиана ранжированного ряда =

Второй тур опроса

Таблица 10 - Результаты второго тура экспертизы

Экспертные

данные

Ранжированный

ряд

Х =

172

Медиана ранжированного ряда =

Таблица 11 - Итоги экспертной оценки метода "Дельфи"

Тур Интервал

Средняя оценка

в туре Х

Дисперсия

Коэффициент

вариации

Результатом экспертизы является медиана ранжиро-

ванного ряда второго тура.

ТЕМА 3. ОСНОВНЫЕ ФОРМАЛИЗОВАННЫЕ МЕТОДЫ

ПРОГНОЗИРОВАНИЯ

Задание 5. Методы прогнозной экстраполяции.

Цель занятия: Освоить методику прогнозирования с

помощью методов экстраполяции.

Задача 1. Дать прогноз урожайности культур мето-

дом скользящей средней.

Содержание:

1. Провести сбор и подготовку исходной информа-

ции по урожайности зерновых за ряд последних лет.

2. Обосновать глубину предпрогнозного периода,

полученные данные нанести на координатное поле и по-

строить интервальный временной ряд.

3. Выявить тенденции изменения урожайности мето-

дом выравнивания по скользящей средней и построить ее

графическое изображение.

4. Выбрать вид аналитической функции.

. Определить параметры уравнения тренда спосо-

бом наименьших квадратов и рассчитать прогнозную уро-

жайность.

Исходная информация:

173

Урожайность выбирается за 10 лет и заносится в табли-

цу 12.

Таблица 12 - Урожайность зерновых культур

Годы (t)

Урожайность (У

), ц/га

Методические указания:

1. Сущность метода экстраполяции заключается в

изучении сложившихся в прошлом устойчивых тенденций

роста урожайности и перенесении их в ближайшее будущее.

Прогнозирование этим методом имеет свои преиму-

щества и недостатки. Преимущества этого метода заклю-

чаются в том, что фактическая урожайность достаточно

точно отражает и плодородие почвы, и климатические ус-

ловия, и уровень агротехники, и организационно-экономи-

ческие мероприятия. Недостаток - этим методом нельзя

учесть прогнозный уровень интенсивности сельскохозяйст-

венного производства на прогнозный период.

. Исходная урожайность выбирается за определен-

ный период. При этом необходимо учесть, что чем длиннее

временной ряд, тем точнее прогноз. Но чрезмерное увели-

чение числа членов в динамическом ряду ведет к преувели-

чению роли прошлого и делает прогноз нечувствительным

к изменениям, наметившимся в последнее время. Опти-

мальной длиной временного ряда является 9-11 лет.

3. Для выявления тенденции изменения показателя (вы-

равнивания) используются различные методы. Чаще всего

используются методы аналитического выравнивания по

скользящей средней.

. Суть метода скользящей средней состоит в замене

фактических значений урожайности их усредненными ве-

личинами, имеющими значительно меньшую вариацию.

174

Для этого последовательно рассчитываются суммы из

m-элементов ряда (как правило m = 3), на основе которых

рассчитываются средние величины, которые изменяются

(скользят) по мере увеличения параметра времени (t).

5. Процесс построения скользящих средних может

повторяться. Полученные результаты наносятся на перво-

начальное координатное поле, как новый временной ряд.

На основе анализа нового временного ряда выбирает-

ся вид аналитической функции, при прогнозировании уро-

жайности обычно используют линейную, реже квадратичес-

кую функцию.

6. Определение параметров уравнения может произ-

водиться несколькими способами. Наиболее распростра-

ненным среди них является способ наименьших квадратов,

позволяющий получить параметры уравнения с таким рас-

четом, чтобы суммарное отклонение фактических значений

ряда от найденных по уравнению было бы минимальным.

Функция У = f(x) наиболее точно отображает исход-

ную зависимость, если выполняется условие:

min)(

→−

∑

7. Поставив уравнение прямой btaY += в условие

минимальности, после соответствующих преобразований

получим систему:











+=⋅

+⋅=

∑ ∑∑

∑ ∑

tbtatу

tbanу

где п - длина временного ряда; а, b - константы.

8. Для определения численных значений констант а и

b необходимо рассчитать все суммы, вошедшие в систему

(

∑∑∑

,, ttу

) и решить систему уравнений.

9. Найденные значения констант подставляются в

уравнение

btaY += , а, подставляя t, находим выровненное

значение урожайности для изучаемой совокупности и про-

гнозную урожайность.

Решение изложить в таблицах 13, 14 и на графике.

175

Таблица 13 - Статистическое выравнивание урожайно-

сти зерновых по методу скользящей средней

Годы

Урожайность,

ц/га

Трехчленные

скользящие

суммы

Трехчленные

скользящие

средние

Трехчленные

скользящие

суммы

Сумма

Таблица 14 - Расчет числовых значений констант

Годы

Урожа

йность

(у

), ц/га

Услов

ный

год (t)

⋅

Выравненная уро-

жайность

у , ц/га

Сумма

176

Решение:

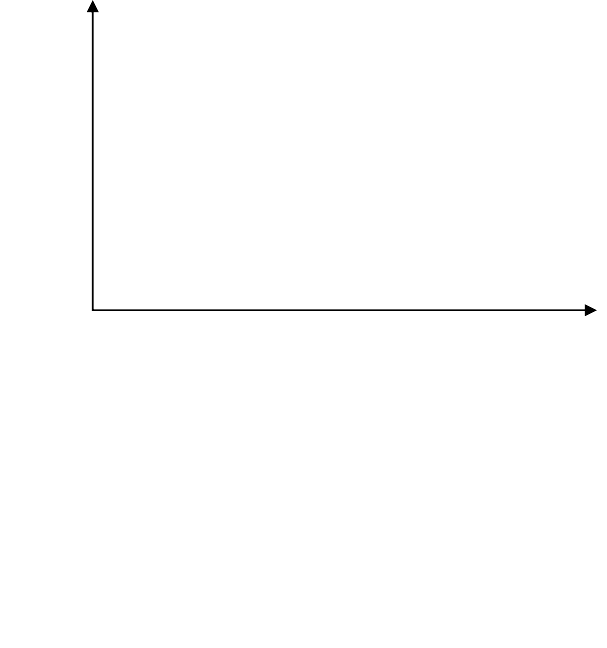
Урожайность, ц/га

Годы

Рис. 20. График урожайности зерновых культур.

Задача 2. Дать прогноз урожайности культур мето-

дом экспоненциального сглаживания.

Содержание:

1. Провести сбор и подготовку исходной информа-

ции по урожайности зерновых за ряд последних

лет.

2. Выявить тенденции изменения урожайности мето-

дом экспоненциального сглаживания.

Исходная информация:

1. Урожайность выбирается за 10 лет и заносится в

таблицу 13 (данные берутся из задачи 1).

. Константа сглаживания

= 0,8.

3. Первый прогноз урожайности =

177

Методические указания:

1. Сущность метода экспоненциального сглаживания

заключается в том, что при анализе временных рядов всем

исходным данным приписываются веса: более поздним

данным придается больший вес, чем более ранним.

2. Константа сглаживания

выбирается из отрезка (0, 1)

3. Прогноз урожайности рассчитывается по формуле:

ttt

FAF ⋅−+⋅=

)1(

αα

где

A - фактический результат в последний период;

F - прогноз в последний период.

4. Программа Excel позволяет быстро провести про-

стое экспоненциальное сглаживание. Сервис → Анализ данных

→ Экспоненциальное сглаживание → ОК. Появляется диа-

логовое окно, которое нужно заполнить. В графе Фактор

затухания указать значение (1 -

) (по умолчанию 0,3). ОК.

Решение изложить в таблице 15.

Задание 6. Методы моделирования.

Цель занятия: Освоить методику прогнозирования с

помощью методов моделирования

Задача 1. Построить сетевой график, используя метод

сетевого моделирования.

Таблица 15 - Прогноз урожайности методом

экспоненциального сглаживания

−

A фактически

−

F прогноз

Прогноз

178

Содержание:

1. Составить сетевой график (логическую схему) про-

ведения работ по определенному проекту.

2. Найти критический путь работ.

3. Определить сколько времени потребуется для за-

вершения проекта.

Таблица 16 - Исходная информация:

Работа

Непосредственный

предшественник

Продолжительность

работы, недель

А -

В -

C A

D A

E B

F D, E

G D, E

H C, F

Методические указания:

1. Самый продолжительный путь сетевого графика от

исходного события к завершающему называется критическим.

2. Продолжительность критического пути определяет

срок выполнения проекта.

3. При расчетах сетевого графика каждый круг, изо-

бражающий событие, делится на четыре сектора:

где 1 – i

– t

(i)

3 – t

(i)

4 – R (i)

1 2

3 4

179

4. Обозначения:

t (i, j) - продолжительность работы с начальным со-

бытием i и конечным событием j.

Ранний срок

t (j) свершения события j - это самый

ранний момент, к которому завершаются все работы, пред-

шествующие этому событию. Правило вычисления:

t (j)= max (

t (i) + t (i, j)), где

Максимум берется по всем событиям i, непосредст-

венно предшествующим событию j (соединены стрелками).

Поздний срок

t (i) свершения события i - это такой

предельный момент, после которого остается ровно столько

времени, сколько необходимо для выполнения всех работ,

следующих за этим событием. Правило вычисления:

t (i) = min (

t (j) - t (i, j)),

где минимум берется по всем событиям j, непосредственно

следующим за событием i.

Решение:

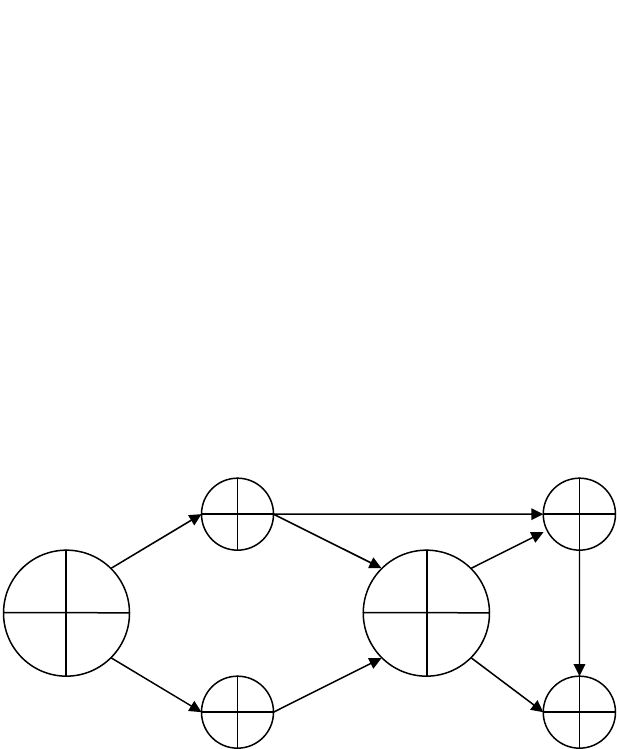
Сетевой график имеет вид:

Рис. 21. Сетевой график.

180

1 этап. При вычислении t

(i) перемещаются по сете-

вому графику от исходного события 1 к завершающему со-

бытию 6.

t (1) = 0

t (2) =

t (3) =

t (4) =

t (5) =

t (6) =

t критическое =

2 этап. При вычислении t

(i) перемещаются от за-

вершающего события 6 к исходному событию 1 по сетево-

му графику против стрелок.

t (6) =

t (5) =

t (4) =

t (3) =

t (2) =

t (1) =

Выводы:

Задача 2. Рассмотреть построение имитационной модели.

Содержание:

1. Используя метод имитационного моделирования,

имитировать прибытие машин в течение 10 часов.

2. Рассчитать вероятность прибытия машин.

. Рассчитать кумулятивную вероятность прибытия

машин.

Исходная информация: