Сиротин Э.Е. Автоматизированные системы управления технологическими процессами. Конспект лекций
Подождите немного. Документ загружается.


161
ях весьма трудоемко.
Цифровые регуляторы и их настройка
Цифровые алгоритмы управления являются важнейшей составной ча-
стью программного обеспечения микропроцессорных контроллеров и вычис-
лительных машин (ЭВМ). ЭВМ осуществляет опрос сигналов с датчиков,
вычисляет значения управляющих сигналов по заданному закону регулиро-
вания, а затем выдает их на исполнительные механизмы. Период опроса
(квантования) изменяется в зависимости от динамических параметров про-
цесса от долей до нескольких десятков секунд.
В настоящее время наблюдается тенденция вытеснения аналоговых
систем управления цифровыми. Объясняется это широкими возможностями
по реализации самых совершенных алгоритмов регулирования, что, в свою
очередь, гарантирует получение высокой точности и хорошего быстродейст-
вия в замкнутой системе непосредственного цифрового управления.
Алгоритмы цифрового ПИД регулирования
Наиболее распространенными алгоритмами являются ПИ и ПИД алго-
ритмы цифрового управления. При правильной настройке эти алгоритмы
обеспечивают достаточно хорошее качество управления для большинства
объектов промышленной технологии.
Рассмотрим процедуру вывода алгоритма цифрового ПИД-регулятора
из соответствующего непрерывного закона, имеющего вид
0
1
( ) ( )
pd
t
ï
de
U t K e t T
dt
T edt
, (8.2)
где
çàä
e y y
– ошибка регулирования.
Запишем уравнение (8.2) в конечных разностях, путем замены
k
t kT
:
0
1 ( ) ( 1)
( ) ( )
()
d
k
k
ïk
i
e k e k
u k e k T
T
T e i T
, (8.3)
где k=1,2,3... – номер периода квантования,
k
T
– величина периода квантова-
ния.
Отметим, что при достаточно малых периодах квантования цифровой
162
ПИД закон управления обеспечивает почти такое же качество процессов
управления, что и исходный непрерывный закон (8.2).
На практике вместо вычислений абсолютных значений управляющего
сигнала удобней вычислять его приращения
()uk
на каждом такте. В этом
случае становится возможным использовать этот алгоритм для управления
объектами, оснащенными как пропорциональным так и интегрирующими
исполнительными механизмами. В результате получаем так называемый
скоростной алгоритм управления, полностью эквивалентный исходному:
( ) ( ) ( 1) ( ) ( 1) ( )
( ) ( 1) ( ( 1) ( 2))
k
p
ï
d
k
T
u k u k u k K e k e k e k
T
T
e k e k e k e k
T
(8.4)
Приведя подобные члены, получим
0 1 2
( ) ( 1) ( ) ( 1) ( 2)
p
u k U k K d e k d e k d e k
, (8.5)
где
0 1 2
1 , 1 2 ,
k d d d
ï k k k
T T T T
d d d
T T T T
, (8.6)
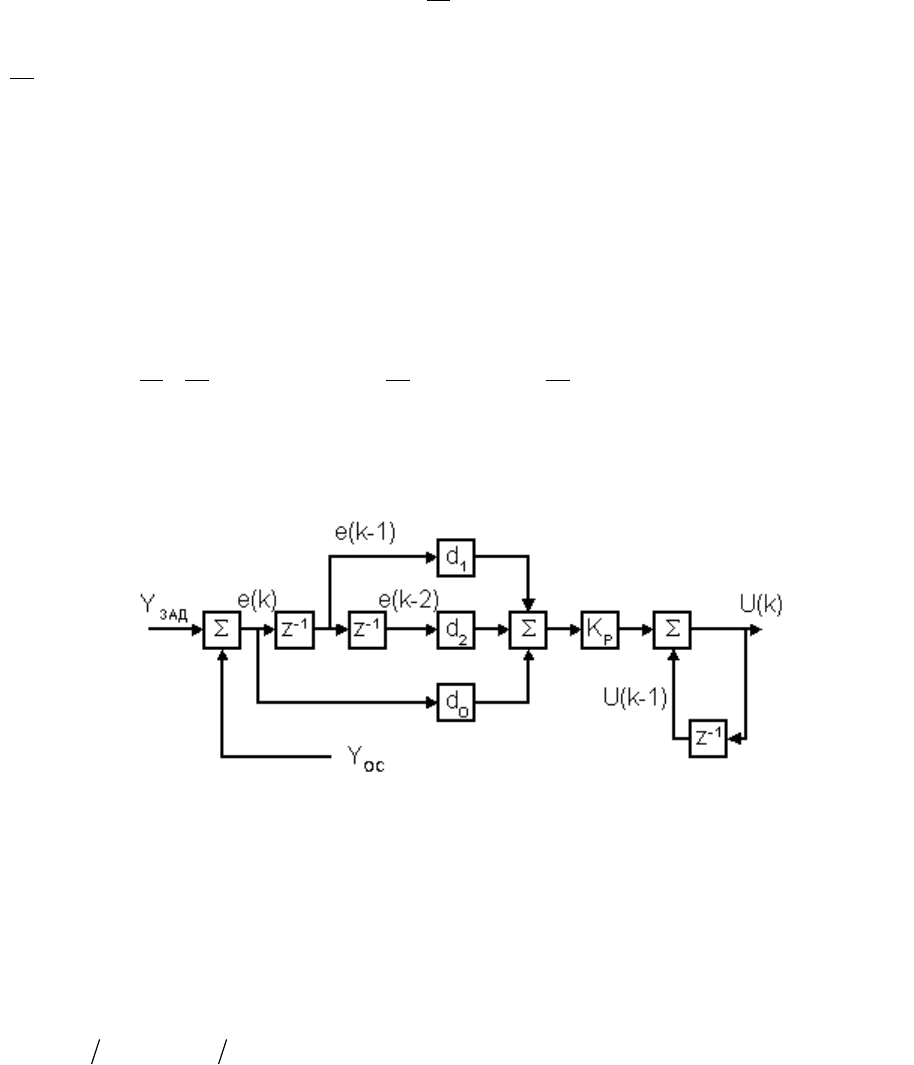
Структурная схема цифрового ПИД регулятора приведена на рис. 8.5,
где через
1
Z
обозначен блок задержки сигнала на один период квантования.
Рисунок 8.5. Структурная схема скоростного ПИД-регулятора.
Выбор периода квантования
Для того, чтобы эффект квантования по времени мало сказывался на
динамику системы цифрового регулирования, рекомендуется выбирать пери-
од квантования из соотношения:
95 95
15 5
k
T T T
,

163
где:
95
T
– это время достижения выходным сигналом уровня 95% от устано-
вившегося значения при подаче на вход объекта ступенчатого сигнала.
Другой подход к выбору величины периода квантования основан на
рекомендациях американских ученых Зиглера и Никольса, согласно которым
0,1
k êð
TT
, где
êð
T
– период критических колебаний объекта управления.
Нельзя выбирать большие периоды квантования, особенно для ответст-
венных процессов, поскольку в этом случае аварийные ситуации будут лик-
видироваться слишком медленно. В тоже время, при слишком малом периоде
квантования повышаются требования к быстродействию ЭВМ и увеличива-
ется влияние шумов.
Упрощенная методика расчета настроек цифрового ПИД регуля-
тора
С целью упрощения процедуры настройки цифрового ПИД-регулятора
рекомендуется (согласно Зиглеру и Никольсу) выбирать следующие значения
отношений:
0,2, 1,25
kd
ïk
TT
TT
,
при
0,1
k êð
TT
, где
êð
T
– период критических колебаний объекта управления.
В этом случае, согласно формулами (8.6), соответствующие коэффици-
енты будут равны:
0 1 2
2,45, 3,5, 1,25d d d
Таким образом настраиваемым параметром остается лишь один коэф-
фициент усиления регулятора
p
K
, чем и объясняется простота и широкая
распространенность этого метода настройки.
Для цифрового ПИ закона управления
( 0)
d
T
получим:
0 1 2
1,2, 1, 0d d d
.
После определения периода квантования
k
T
единственным настраивае-
мым параметром в алгоритме (8.5) является коэффициент усиления цифрово-
го регулятора
p
K
. Его достаточно просто настроить экспериментально, так
чтобы декремент затухания в системе был равен 1,4 (D=1/4).
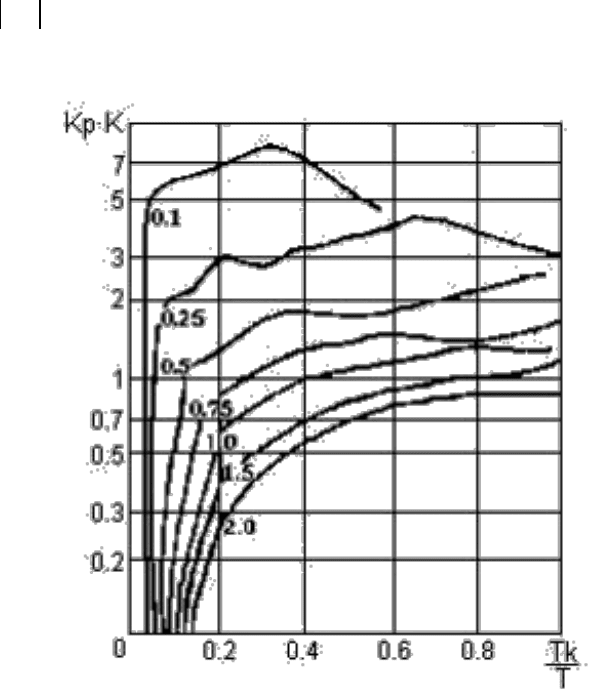
Однако при известных параметрах объекта управления определение
величины КР возможно с помощью номограмм, приведенных на рис. 8.6 и
8.7. Эти номограммы построены с помощью ЭВМ путем минимизации инте-
164
грального критерия качества по величине
p
K
:
0
( ) min
t
J t e t dt
по
p
K
.
Рисунок 8.6 Номограмма для ПИ-регулятора.
165
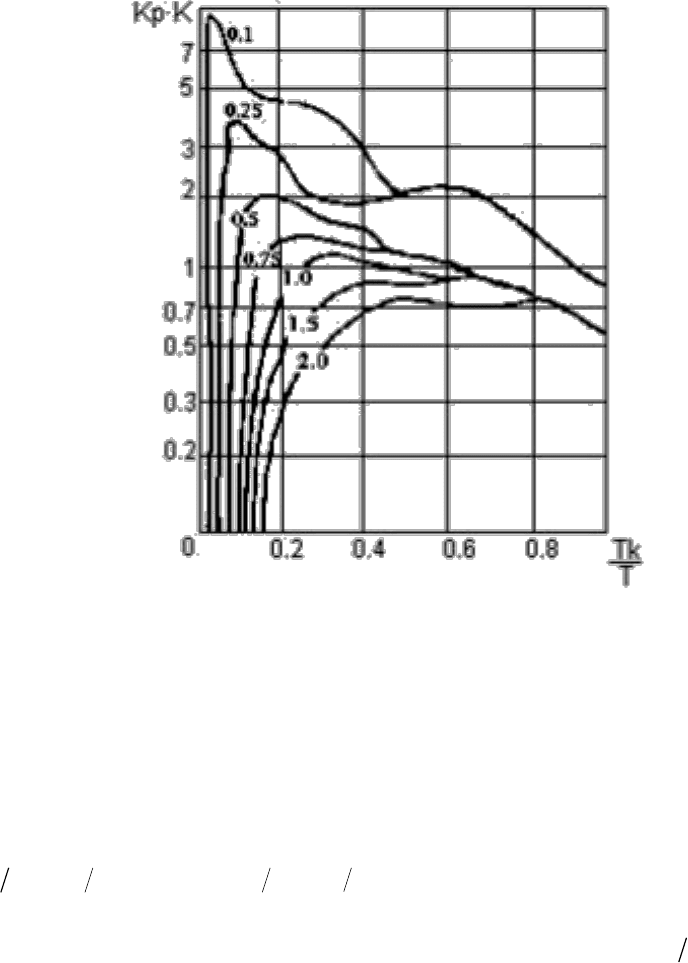
Рисунок 8.7. Номограмма для ПИД-регулятора.
Пример [32]. Определить настройки цифрового ПИ-регулятора для
объекта первого порядка с запаздыванием, с параметрами: К = 2,4; Т =612 c;
480
c;
k
T
=120 c.
Для определения величины
p
K
необходимо определить отношения:
480 612 0,78; 120 6120 0,196
k
T T T
.
По номограмме рис. 8.6 найдем
0,85
p
KK
, тогда
0,85 2,4 0,354
p
K
.
Расчет настроек цифрового регулятора по формулам
Здесь, как и ранее, предполагается, что переходная характеристика
объекта управления аппроксимирована звеном первого порядка c запаздыва-
нием. При этом, с целью исключения (уменьшения) бросков управляющего
сигнала при ступенчатом изменении сигнала задания, используется несколь-
ко другая форма записи дискретного ПИД- закона управления, а именно
12
( ) ( 1) ( 1) ( ) ( ) (2 ( 2) ( ))
p çàä
u k u k K y k y k d y y k d y k y k
Выбрав период квантования
k
T
, рассчитывают параметры настройки

166
дискретного ПИ- или ПИД-регулятора по формулам:
Для ПИ-регулятора:
*
2
*
12
*2
0,135
0,9
,
2 ( 2)
0,27
, 0,
( 2)
k
p
kk
p
k
p
pk
TT
T
K
TT
K
TT
d d K
K T K
Для ПИД-регулятора:
*
2
*
12
* 2 *
0,3
1,2
,
( 2)
0,6
0,5
,,
( 2)
k
p
kk
p
k
p
p k p k
TT
T
K
TT
K
TT
T
d d K
K T K T K
В этих формулах учтено запаздывание на величину
/2
k
T
, свойственное
всем замкнутым цифровым системам регулирования.
ПОКАЗАТЕЛИ ЭФФЕКТИВНОСТИ АВТОМАТИЗАЦИИ ТЕХ-
НОЛОГИЧЕСКИХ ПРОЦЕССОВ.
Качество работы сложной системы оценивается при помощи показате-
лей эффективности.
Под показателем эффективности сложной системы понимают такую
числовую характеристику, которая оценивает степень приспособленности
системы к выполнению основной цели.
В качестве показателей эффективности сложных технических систем
(СТС) принимают производительность измеряемую как:
cp
ïë
N
Q
T
, (8.7)
где N
ср
– среднее число изделий, T
пл
– плановый период времени.
Показатели эффективности СТС зависят как от параметров системы
1
,
2
, ...,
n
, так и параметров, характеризующих воздействие внешней среды
1
,
2
,..., m:
Q = Q(
1
,
2
, ...,
n
;
1
,
2
,..., m) (8.8)
Экономические показатели эффективности W
t
связаны со стоимостью
167
продукции Ц
t
в оптовых ценах, произведенных за время t, себестоимостью C
t
и капитальными вложениями К:
W
t
= (Ц
t
, C
t
, К) (8.9)
Прибыль за время t П
1
и чистая прибыль П
2
определяются по форму-
лам:
П
1
= Ц
t
- C
t
(8.10)
П
2
= Ц
t
– С
t
– E
н
К (8.11)
где E
н
- нормативный коэффициент экономической эффективности ка-
питальных вложений.
Для современных технических систем (ТС) важнейшее значение имеет
надежность функционирования. По мере усложнения систем становится бо-
лее сложной и оценка их надежности. К сложной системе не применимы та-
кие показатели надежности как вероятность безотказной работы , среднее
время безотказной работы, так как они констатируют лишь сам факт отказа и
не позволяют получить представление о влиянии отказа на конечный эффект
функционирования системы.
Пусть величина R является показателем эффективности некоторой
сложной системы, тогда величина R
а
, показывает, насколько снижается эф-
фективность системы за счет возможных отказов ее элементов по сравнению
с эффективностью идеальной системы R
o
:
R
а
= R
o
– R (8.12)
Повысить функциональную надежность и точность ТС можно двумя
способами:
1. увеличением надежности функциональных элементов, что связано
с использованием новых физических принципов, повышением чистоты мате-
риалов, более высокой технологической дисциплиной производства;
2. улучшением организации системы путем синтеза надежной систе-
мы из малонадежных элементов. Этот способ связан с использованием избы-
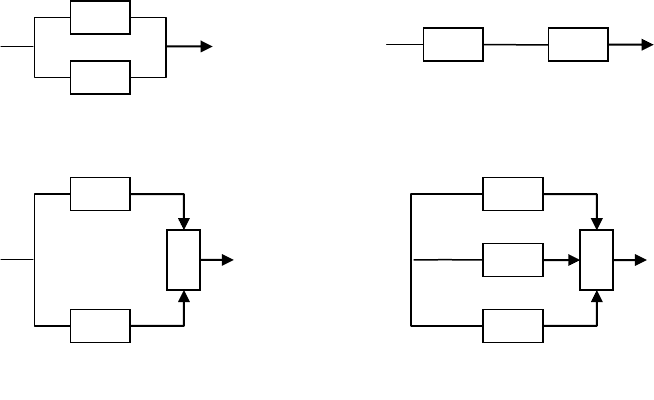
точности разного вида: резервированием (при обрыве (рис. 8.8,а) или замы-
кании в элементах (рис. 8.8,б) система будет оставаться работоспособной,
хотя параметр эффективности изменится); дублированием (рис. 8.8,в) или с
утроением и мажоритарным выбором результата (рис. 8.8,г).
168
Рисунок 8.8 Резервирование элементов ТС.
Качество управления зависит от наличия состава управляющих уст-
ройств, качества алгоритмов управления, частоты циклов управления.
Качество управления характеризуется величиной R
упр
, которая пока-
зывает насколько снижается эффективность управления по варианту А, по
сравнению с эффективностью управления по варианту В:
R R R
ÀÂ
óï ð óï ð óï ð
(8.13)
Процесс функционирования любой сложной системы подвержен влия-
нию случайных факторов, связанных с внутренними состояниями системы и
воздействиями окружающей среды. Поэтому помехозащищѐнность ТС
должна быть достаточно высокой, чтобы обеспечить ее нормальное функ-
ционирование.
Внутренние помехи проявляются в виде изменений свойств парамет-
ров элементов:
i
=
i0
+
i
,
(8.14)
где
i
– изменение параметров, вызванные действием помех.
Внешние помехи проявляются в отклонениях от нормы в результате
воздействия на сложную систему внешней среды:
i
=
i0
-
i
(8.15)
Тогда показатель эффективности системы при действии на нее внут-
ренних и внешних помех:
а)
б)
1
2
в)
г)
169
R
пом
= R(
1
,
2
,
3
,…,
п
;
1
,
2
,
3
,…,
п
), (8.16)
а величина разности:
R
пом
= R
0
- R
пом
(8.17)
является показателем помехозащищенности системы.
Устойчивостью функционирования сложной системы называется
способность системы сохранять свои функции в условиях действия возму-
щений. Обычно рассматривают область устойчивости на множестве дейст-
вующих внешних и внутренних факторов.
Сложностью системы S, состоящей из элементов со сложностью Si,
(где i=l,2,...,N), называется величина:
i
1
S Si K ,
N
i
(8.18)
где K
i
– число элементов i-ro типа, входящих в систему.
Максимальное число связей в системе, состоящей из N элементов,
N(N-1), а фактическое число связей в системе – M. Тогда величина:
а = M / N(N – 1) (8.19)
характеризует относительное число реализованных связей,а сложность сис-
темы выразится как:
ii
1
S (1 a) S K
N
i
(8.20)
где - коэффициент, учитывающий сложность связей по сравнению со слож-
ностью элементов системы.

170
Под функциональной надѐжностью Р
ф
понимают вероятность того,
что данная система будет удовлетворительно выполнять свои функции в те-
чении заданного времени.
Прежде чем произвести оценку надѐжности системы в целом, необхо-
димо найти показатели надѐжности отдельных еѐ звеньев (подсистем). Для
этого следует определить их состав на основе анализа структурной схемы
данной (или проектируемой) системы. Необходимо также выделить комплекс
устройств (подсистем), всякий отказ в работе которых приводит к отказу
всей системы. В АСУТП таким устройством (основным), как правило, явля-
ется ЭВМ.
После этого необходимо установить функциональные связи основного
устройства с дополнительными, которые в процессе работы системы время
от времени подключаются к основному устройству на время τi для обмена и
обновления информации. Очевидно, что влияние таких устройств будет оп-
ределяться главным образом тем, какова вероятность нахождения этих уст-
ройств в рабочем состоянии в любой произвольный момент времени t.
Таким образом, функциональная надѐжность системы зависит от безот-
казной работы как основного устройства (комплекса) в заданное время, так и
дополнительных устройств, работающих совместно с основным в течение
времени τ:
0
{ ( ); ; ( )}
ô i i i
P f P t ê P
, (8.21)
где
0
()Pt
– вероятность безотказной работы основного элемента; к
i
– ко-
эффициент готовности i-го устройства; Р
i
(τ
i
) – вероятность безотказной ра-
боты i-го дополнительного устройства при совместной работе с основным за
среднее время при решении основной задачи.
Так как вся система работает в основном режиме, то еѐ функциональ-
ная надѐжность определяется по зависимости
0
1
( ) ( )
m
ô i i
i
P P t ê P
, (8.22)
где m – количество дополнительных устройств в системе.
Если резервирования в системе нет, то
0
1
0
1
( ) ; ( ) ; 1
1
i
i i i
t
ii
i
P t e P t e ê e
, (8.23)
где λ
0
, λ
i
– соответственно средняя интенсивность отказов основного и
дополнительного устройств;
1
;
i
i i i
i
– среднее время восстановления рабочего состояния уст-
