Simon Benninga. Financial Modelling 3-rd edition
Подождите немного. Документ загружается.

18 Chapter 1
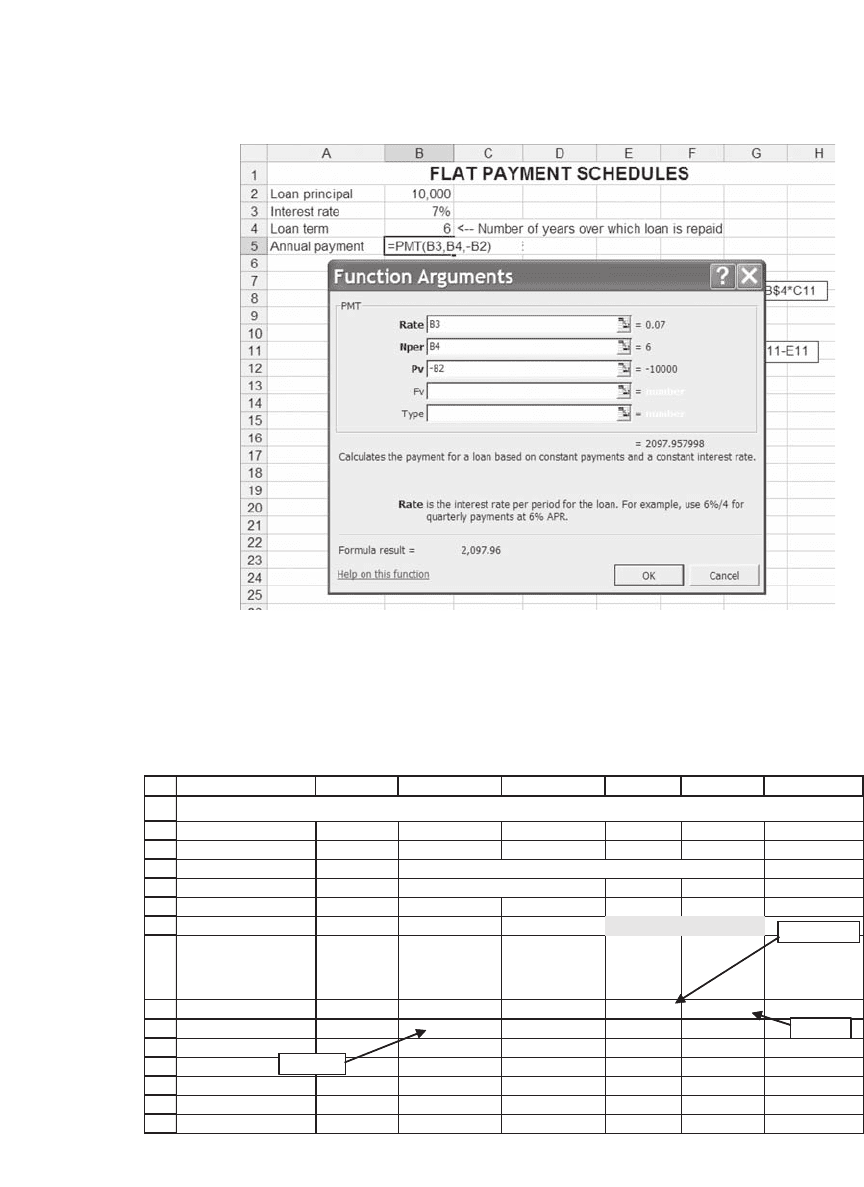
Notice that we have put a minus sign in the space labeled Pv—Excel’s
nomenclature for the initial loan principal. As discussed in footnote 3, if
we do not do so, Excel returns a negative payment (a minor irritant).
You can confi rm that the answer of $2,097.96 is correct by creating a loan
table:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ABCDEFG
Loan principal 10,000
Interest rate 7%
Loan term 6 <-- Number of years over which loan is repaid
Annual payment 2,097.96 <-- =PMT(B3,B4,-B2)
Split payment into:
Year
Principal
at beginning
of year
Payment at
end of year
Interest
Return of
principal
1 10,000.00 2,097.96 700.00 1,397.96
2 8,602.04 2,097.96 602.14 1,495.82
3 7,106.23 2,097.96 497.44 1,600.52
4 5,505.70 2,097.96 385.40 1,712.56
5 3,793.15 2,097.96 265.52 1,832.44
6 1,960.71 2,097.96 137.25 1,960.71
7 0.00
FLAT PAYMENT SCHEDULES
=$B$3*C9
=D9-E9
=C9-F9
19 Basic Financial Calculations
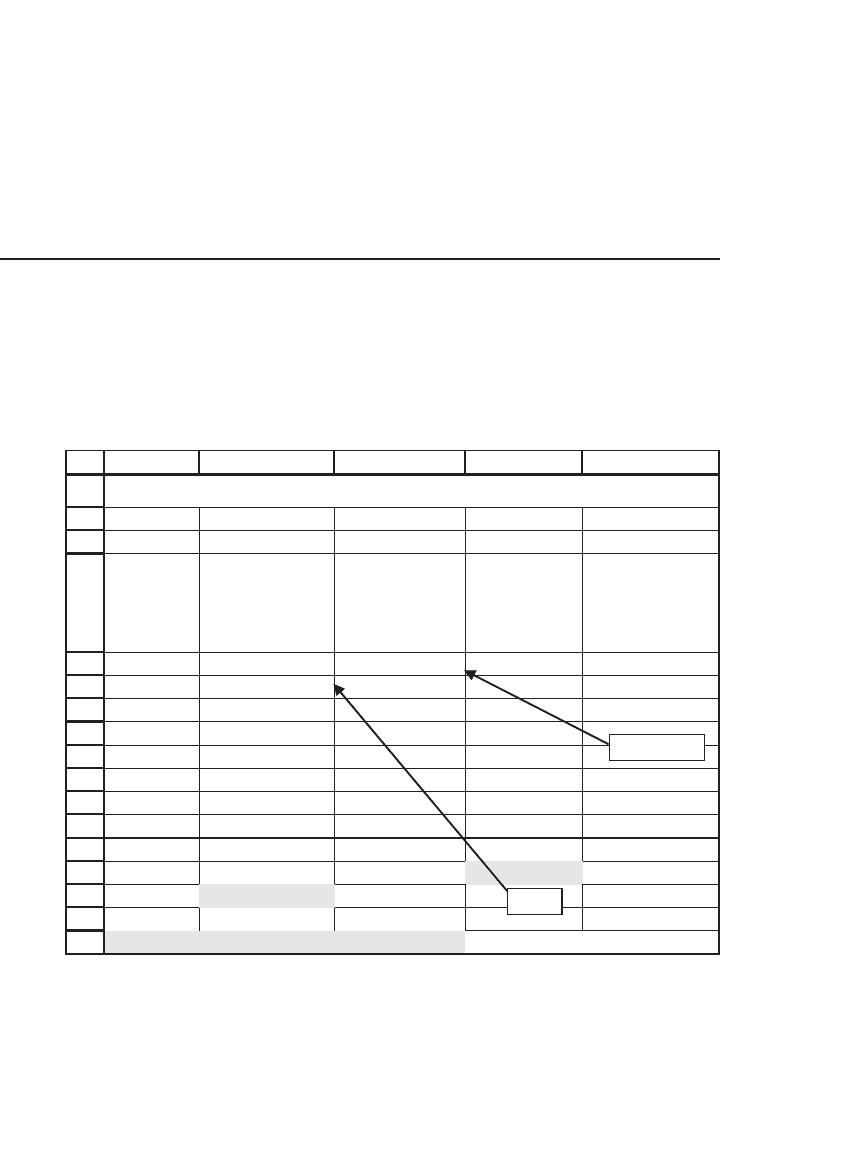
The zero in cell C15 indicates that the loan is fully repaid over its term
of six years. You can easily confi rm that the present value of the pay-
ments over the six years is the initial principal of $10,000.
1.6 Future Values and Applications
We start with a triviality. Suppose you deposit $1,000 in an account today,
leaving it there for 10 years. Suppose the account draws annual interest
of 10 percent. How much will you have at the end of 10 years? The
answer, as shown in the following spreadsheet, is $2,593.74:
As cell C17 shows, you don’t need all these complicated calculations:
The future value of $1,000 in 10 years at 10 percent per year is given
by
FV =∗+ =1 000 1 10 2 593 74
10
,%,() .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
AB C D E
Interest 10%
Year
Account
balance,
beginning of
year
Interest
earned
during year
Total in
account,
end year
1 1,000.00 100.00 1,100.00 <-- =C5+B5
2 1,100.00 110.00 1,210.00 <-- =C6+B6
3 1,210.00 121.00 1,331.00
4 1,331.00 133.10 1,464.10
5 1,464.10 146.41 1,610.51
6 1,610.51 161.05 1,771.56
7 1,771.56 177.16 1,948.72
8 1,948.72 194.87 2,143.59
9 2,143.59 214.36 2,357.95
10 2,357.95 235.79 2,593.74
11 2,593.74
A simpler way 2,593.74 <-- =B5*(1+B2)^10
SIMPLE FUTURE VALUE
=D5
=$B$2*B5

20 Chapter 1
Thus the answer is that we will have $17,531.17 in the account at the
end of year 10. This same answer can be represented as a formula that
sums the future values of each deposit:
Total at beginning of year , % , %10 1 000 1 10 1 000 1 10
10 9
=∗+ +∗+
+
() ()
.... ( )
()
+∗+
=∗+
=
∑
1 000 1 10
1 000 1 10
1
1
10
,%
,%
t
t
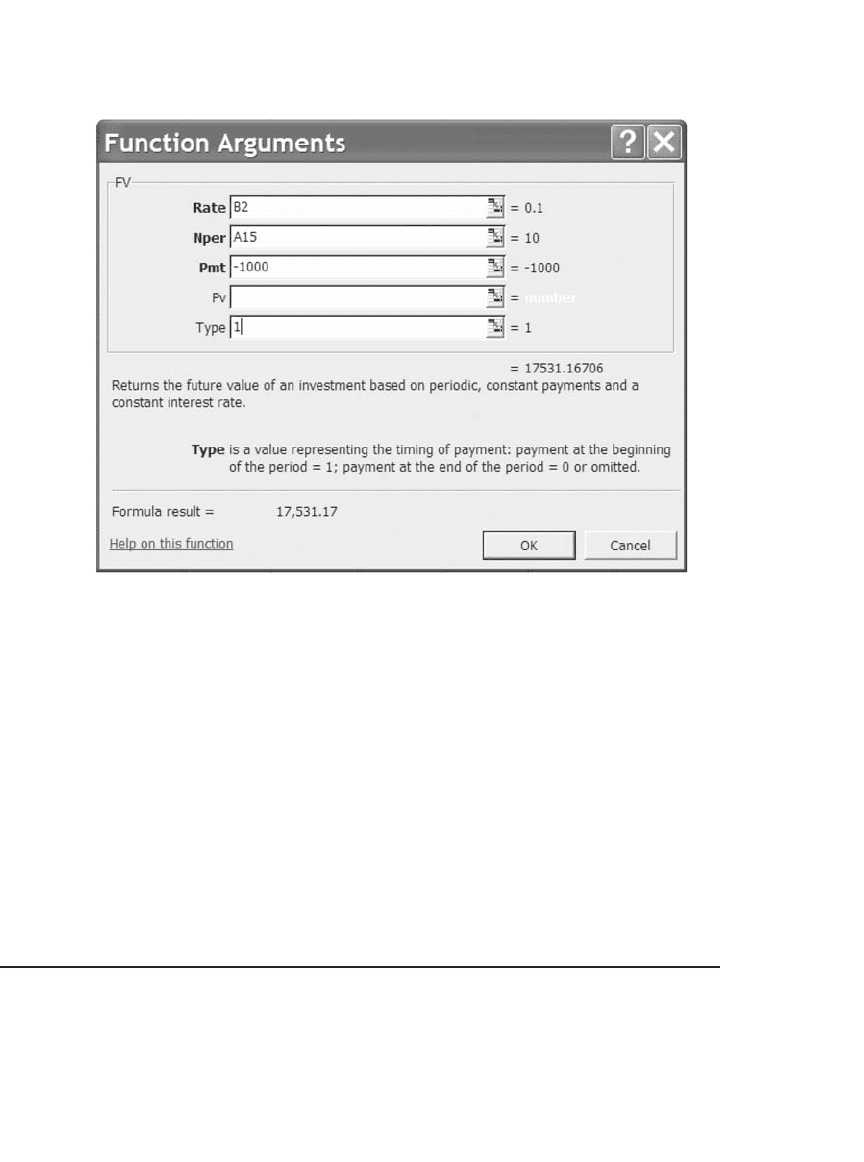
An Excel Function Note from cell B18 that Excel has a function FV
that gives this sum. The dialog box brought up by FV is the following:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
ABCDEF
Interest 10%
Annual deposit 1,000 <-- Made today and at beginning of each of next 9 years
Number of deposits 10
Year
Account
balance,
beginning of
year
Deposit at
beginning
of year
Interest
earned
during year
Total in
account,
end year
1 0.00 1,000 100.00 1,100.00 <-- =D7+C7+B7
2 1,100.00 1,000 210.00 2,310.00 <-- =D8+C8+B8
3 2,310.00 1,000 331.00 3,641.00
4 3,641.00 1,000 464.10 5,105.10
5 5,105.10 1,000 610.51 6,715.61
6 6,715.61 1,000 771.56 8,487.17
7 8,487.17 1,000 948.72 10,435.89
8 10,435.89 1,000 1,143.59 12,579.48
9 12,579.48 1,000 1,357.95 14,937.42
10 14,937.42 1,000 1,593.74 17,531.17
Future value 17,531.17 <-- =FV(B2,B4,-B3,,1)
FUTURE VALUE WITH ANNUAL DEPOSITS
=$B$2*(B7+C7)
=E7
Now consider the following, slightly more complicated, problem:
Again, you intend to open a savings account. Your initial deposit of
$1,000 today will be followed by a similar deposit at the beginning of
years 1, 2, 9. If the account earns 10 percent per year, how much will you
have in the account at the start of year 10?
This problem is easily modeled in Excel:
21 Basic Financial Calculations
We note three things about this function:
1. For positive deposits FV returns a negative number (look back at
footnote 2). This is an irritating property of this function that it shares
with PV and PMT. To avoid negative numbers, we have put the Pmt in
as −1,000.
2. The line Pv in the dialog box refers to a situation where the account
has some initial value other than 0 when the series of deposits is made.
In this example, this space has been left blank, indicating that the initial
account value is zero.
3. As noted in the picture, “Type” (either 1 or 0) refers to whether the
deposit is made at the beginning or the end of each period (in our
example the former is the case).
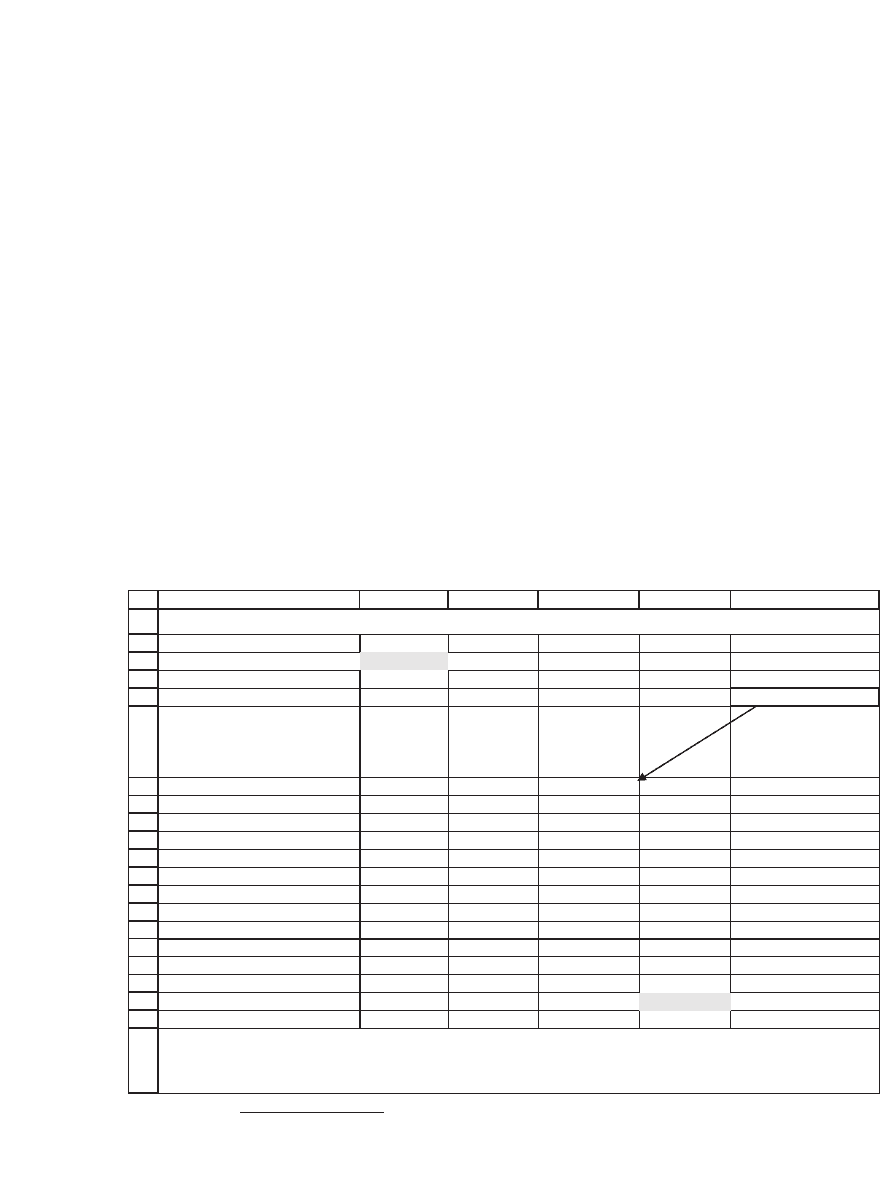
1.7 A Pension Problem—Complicating the Future-Value Problem
A typical exercise is the following: You are currently 55 years old and
intend to retire at age 60. To make your retirement easier, you intend to
start a retirement account.
22 Chapter 1
•
At the beginning of each of years 1, 2, 3, 4 (that is, starting today and
at the beginning of each of the next four years), you intend to make a
deposit into the retirement account. You think that the account will earn
8 percent per year.
•
After retirement at age 60, you anticipate living eight more years.
5
At
the beginning of each of these years you want to withdraw $30,000 from
your retirement account. Your account balances will continue to earn 8
percent.
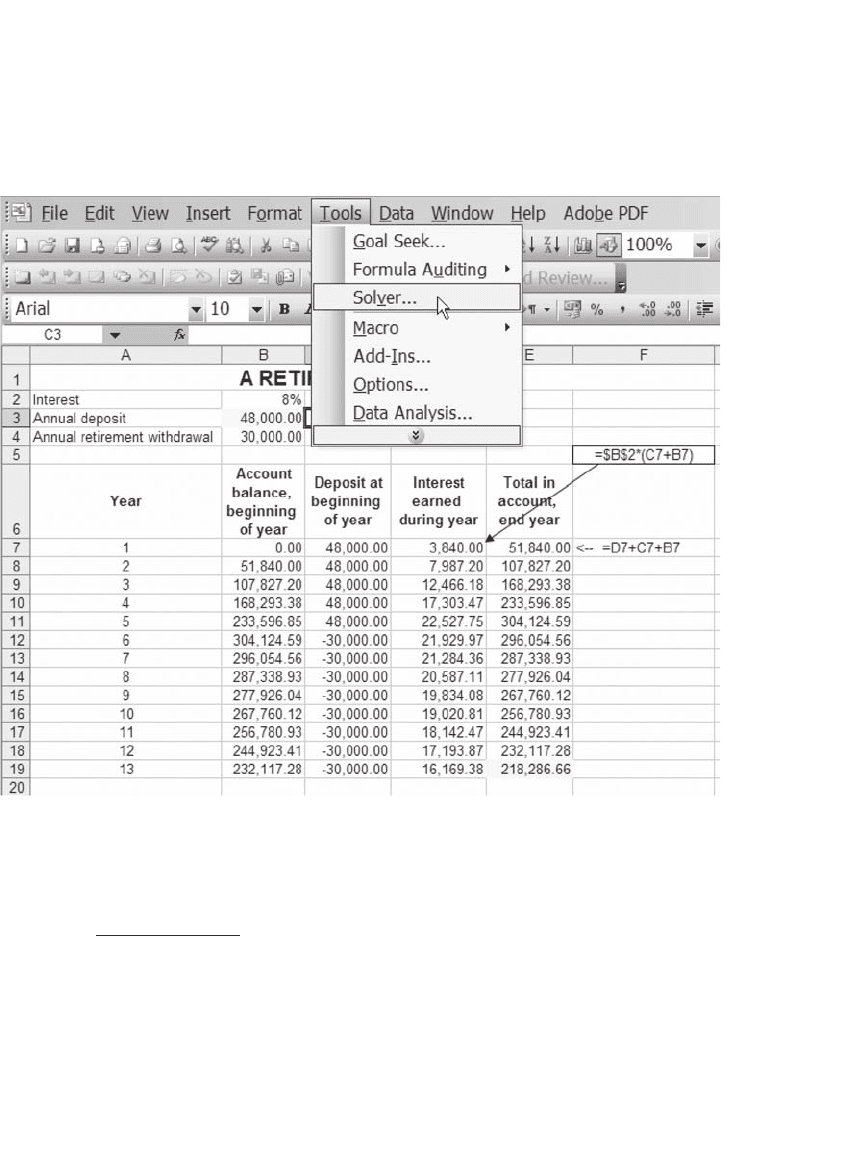
How much should you deposit annually in the account? The following
spreadsheet fragment shows how easily you can go wrong in this kind of
problem—in this case, you’ve calculated that in order to provide $30,000
per year for eight years, you need to contribute $240,000/5 = $48,000 in
each of the fi rst fi ve years. As the spreadsheet shows, you’ll end up with
a lot of money at the end of eight years! (The reason—you’ve ignored
the powerful effects of compound interest. If you set the interest rate in
the spreadsheet equal to 0 percent, you’ll see that you’re right.)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
ABCDEF
Interest 8%
Annual deposit 48,000.00
Annual retirement withdrawal 30,000.00
=$B$2*(C7+B7)
Year
Account
balance,
beginning
of year
Deposit at
beginning
of year
Interest
earned
during year
Total in
account,
end year
1 0.00 48,000.00 3,840.00 51,840.00 <-- =D7+C7+B7
2 51,840.00 48,000.00 7,987.20 107,827.20
3 107,827.20 48,000.00 12,466.18 168,293.38
4 168,293.38 48,000.00 17,303.47 233,596.85
5 233,596.85 48,000.00 22,527.75 304,124.59
6 304,124.59 -30,000.00 21,929.97 296,054.56
7 296,054.56 -30,000.00 21,284.36 287,338.93
8 287,338.93 -30,000.00 20,587.11 277,926.04
9 277,926.04 -30,000.00 19,834.08 267,760.12
10 267,760.12 -30,000.00 19,020.81 256,780.93
11 256,780.93 -30,000.00 18,142.47 244,923.41
12 244,923.41 -30,000.00 17,193.87 232,117.28
13 232,117.28 -30,000.00 16,169.38 218,286.66
A RETIREMENT PROBLEM
Note: This problem has five deposits and eight annual withdrawals, all made at the beginning of the year.
The beginning of year 13 is the last year of the retirement plan; if the annual deposit is correctly
computed, the balance at the beginning of year 13 after the withdrawal should be zero.
5. Of course you’re going to live much longer! And I wish you good health! The dimen-
sions of this problem have been chosen to make it fi t nicely on a page.
23 Basic Financial Calculations
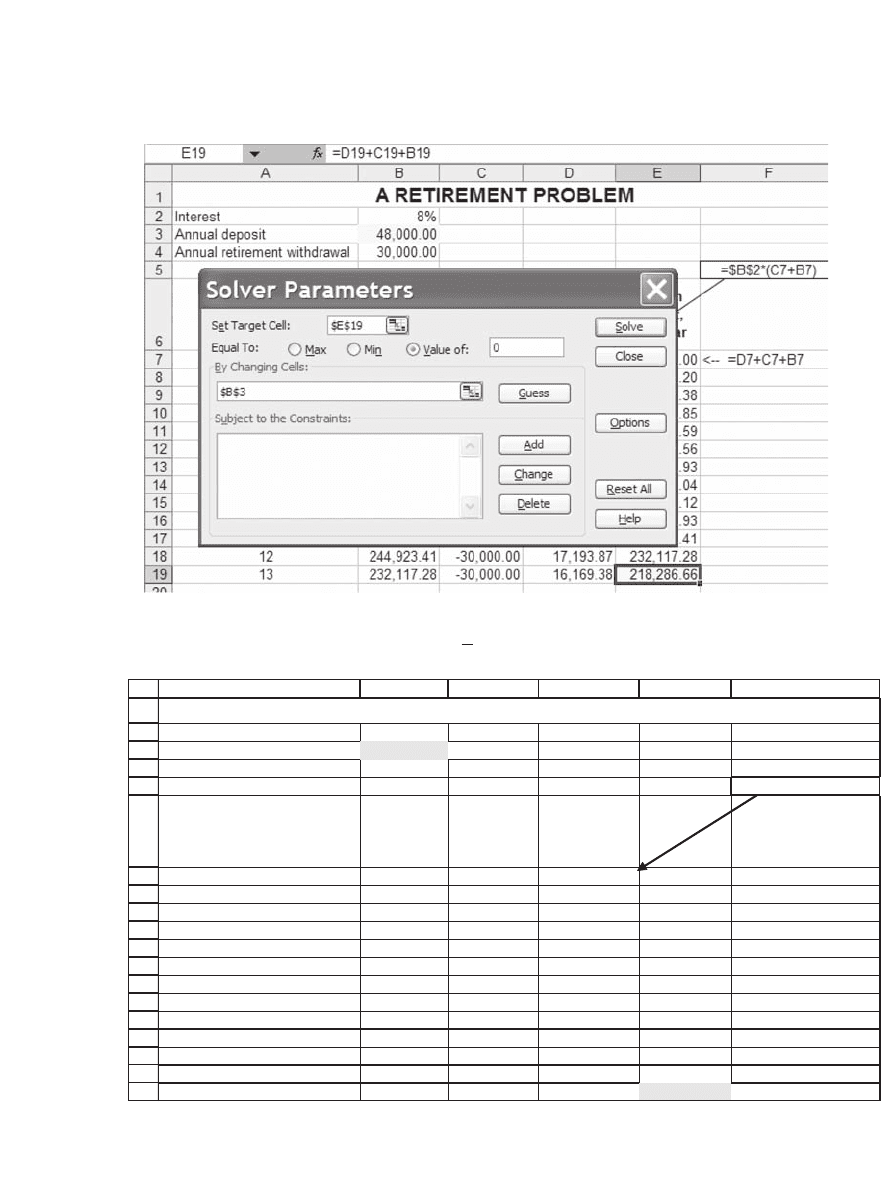
There are several ways to solve this problem. The fi rst involves Excel’s
Solver. This can be found on the Tools menu.
6
6. If the Solver does not appear on the Tools menu, then you have to load it. Go
Tools|Add-Ins and click Solver Add-In on the list of programs. Note that you could
also use the Goal Seek tool to solve this problem. For simple problems such as this
one, there is not much difference between the Solver and Goal Seek; the one (not
inconsiderable) advantage of the Solver is that it remembers its previous arguments,
so that if you bring it up again on the same spreadsheet, you can see what you did in
the previous iteration. In later chapters we will illustrate problems that cannot be
solved by Goal Seek and where the use of the Solver is a necessity. Solver and Goal
Seek are compared in Chapter 6, page 210.
Clicking on the Solver makes a dialog box appear. In the following
illustration we’ve fi lled it in.
24 Chapter 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
ABCDEF
Interest 8%
Annual deposit 29,386.55
Annual retirement withdrawal 30,000.00
=$B$2*(C7+B7)
Year
Account
balance,
beginning
of year
Deposit at
beginning
of year
Interest
earned
during year
Total in
account,
end year
1 0.00 29,386.55 2,350.92 31,737.48 <-- =D7+C7+B7
2 31,737.48 29,386.55 4,889.92 66,013.95
3 66,013.95 29,386.55 7,632.04 103,032.54
4 103,032.54 29,386.55 10,593.53 143,012.62
5 143,012.62 29,386.55 13,791.93 186,191.10
6 186,191.10 -30,000.00 12,495.29 168,686.39
7 168,686.39 -30,000.00 11,094.91 149,781.30
8 149,781.30 -30,000.00 9,582.50 129,363.81
9 129,363.81 -30,000.00 7,949.10 107,312.91
10 107,312.91 -30,000.00 6,185.03 83,497.94
11 83,497.94 -30,000.00 4,279.84 57,777.78
12 57,777.78 -30,000.00 2,222.22 30,000.00
13 30,000.00 -30,000.00 0.00 0.00
A RETIREMENT PROBLEM
If we now click on the Solve box, we get the answer:
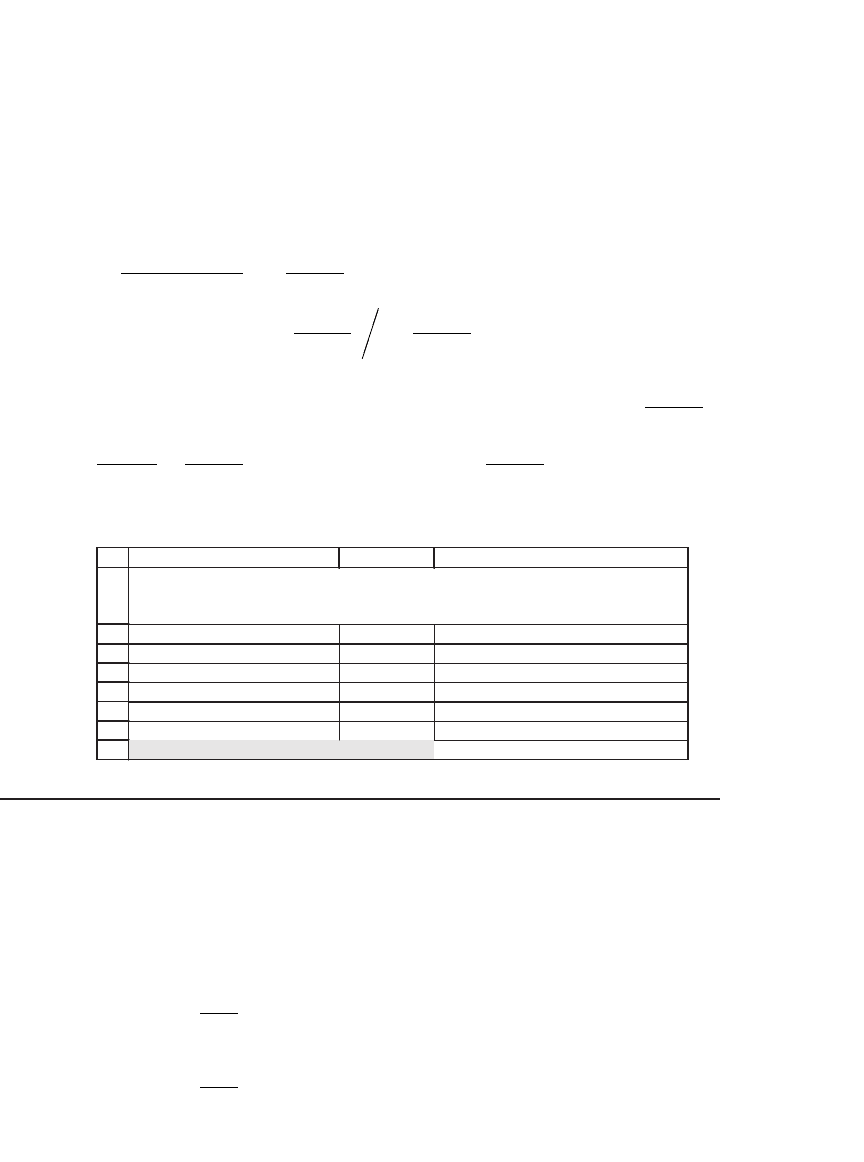
25 Basic Financial Calculations
1.7.1 Solving the Retirement Problem Using Financial Formulas
We can solve this problem in a more intelligent fashion if we understand
the discounting process. The present value of the whole series of pay-
ments, discounted at 8 percent, must be zero:
Initial deposit ,
Initial de
(. ) (. )108
30 000
108
0
0
4
5
12
t
t
t
t==
∑∑
−=
⇒
pposit
,
=
⎡
⎣
⎢
⎤
⎦
⎥
⎡
⎣
⎢
⎤
⎦
⎥
==
∑∑
30 000
108
1
108
5
12
0
4
(. ) (. )
t
t
t
t
Both the numerator on the right-hand side as
30 000
108
5
12
,
(. )
t
t=
∑
=
1
108
30 000
108
4
1
8
(. ) (. )
,
t
t=
∑
and the denominator
1
108
0
4
(. )
t
t=
∑
can be calculated
using Excel’s PV function:
1
2
3
4
5
6
7
8
CBA
Interest 8%
Annual deposit 48,000.00
Annual retirement withdrawal 30,000.00
Numerator 126,718.54 <-- =1/(1+B2)^4*PV(B2,8,-B4)
Denominator 4.31 <-- =PV(B2,5,-1,,1)
Annual deposit 29,386.55 <-- =B6/B7
A RETIREMENT PROBLEM
Solution using formulas
1.8 Continuous Compounding
Suppose you deposit $1,000 in a bank account that pays 5 percent
per year. At the end of the year you will have $1,000
*
(1.05) = $1.050.
Now suppose that the bank interprets “5 percent per year” to mean
that it pays you 2.5 percent interest twice a year. Thus after six
months you’ll have $1,025, and after one year you will have
$
.
$.1 000 1
005
2
1 050 625
2
,,∗+
⎛
⎝
⎜
⎞
⎠
⎟
=
. By this logic, if you get paid interest n
times per year, your accretion at the end of the year will be
$
.
1 000 1
005
, ∗+
⎛
⎝
⎜
⎞
⎠
⎟
n
n
. As n increases, this amount gets larger, converging

26 Chapter 1
(rather quickly, as you will soon see) to e
0.05
, which in Excel is written as
the function Exp. When n is infi nite, we refer to this practice as continu-
ous compounding. (By typing Exp(1) in a spreadsheet cell, you can see
that e = 2.7182818285. . . .)
As you can see in the next display, $1,000 continuously compounded
for one year at 5 percent grows to $1,000
*
e
0.05
= $1,051.271 at the end
of the year. Continuously compounded for t years, it will grow to $1,000
*
e
005
*
t
, where t need not be a whole number (for example, when t = 4.25,
then the accumulation factor e
0.05
*
4.25
measures the growth of the initial
investment at 5 percent annually, continuously compounded for four
years and three months).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
CBA
Initial deposit 1,000
Interest rate 5%
Number of compounding periods per year 2
Interest per compounding period 2.500% <-- =B3/B4
Accretion in one year 1,050.625 <-- =B2*(1+B5)^B4
Continuous compounding with
Exp
1,051.271 <-- =B2*EXP(B3)
Compounding periods per year
End-year
accretion
1 1,050.000 <-- =$B$2*(1+$B$3/A25)^A25
2 1,050.625 <-- =$B$2*(1+$B$3/A26)^A26
10 1,051.140
20 1,051.206
50 1,051.245
100 1,051.258
150 1,051.262
300 1,051.267
800 1,051.269
MULTIPLE COMPOUNDING PERIODS
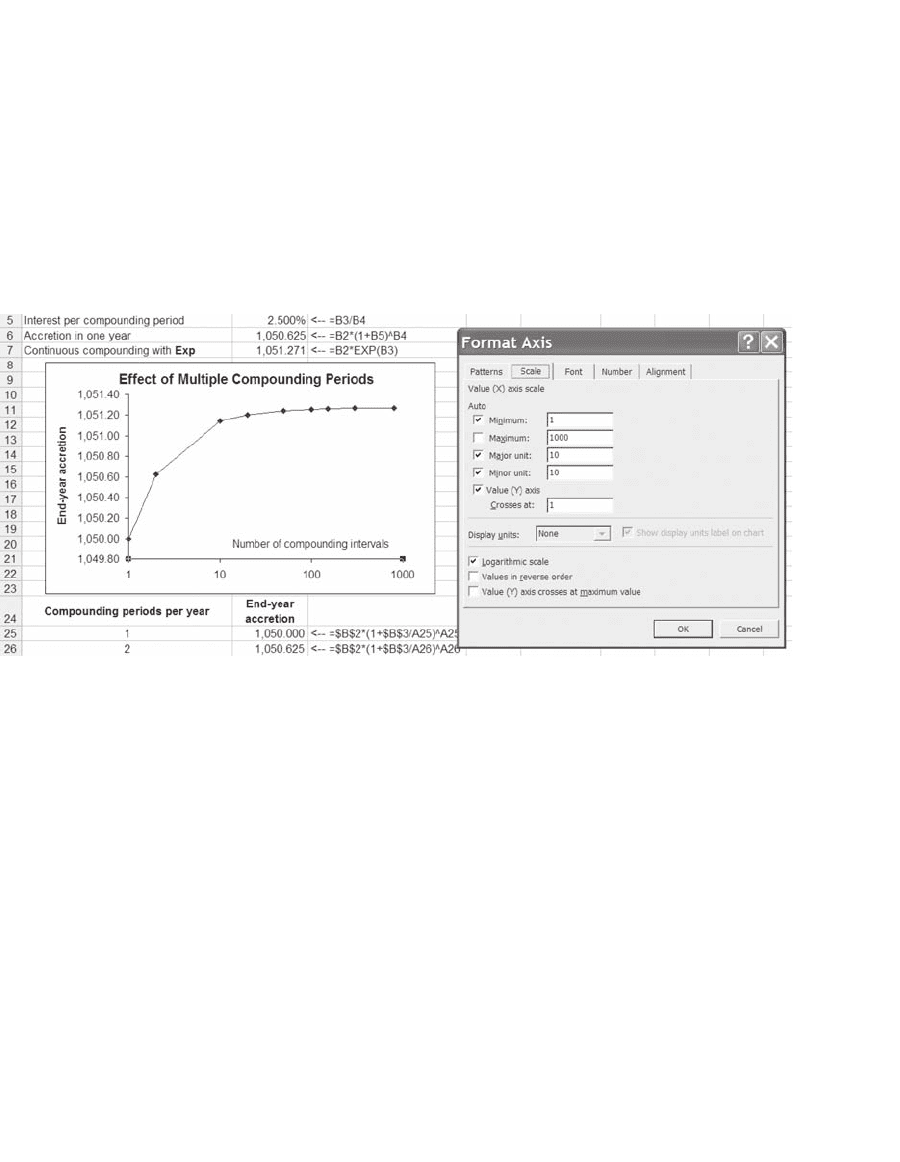
Effect of Multiple Compounding Periods
1,049.80
1,050.00
1,050.20
1,050.40
1,050.60
1,050.80
1,051.00
1,051.20
1,051.40
1 10 100 1000
Number of compounding intervals
End-year accretion
27 Basic Financial Calculations
1.8.1 A Technical Note on the Graph
The graph is an Excel XY (Scatter) chart; the x-axis in the chart has
been set to be in logarithmic scale. This emphasizes the compounding
process. The following picture shows the graph’s x-axis marked and the
relevant dialog box (right-click after marking the axis and go to Format
Axis).
1.8.2 Back to Finance—Continuous Discounting
If the accretion factor for continuous compounding at interest r over t
years is e
rt
, then the discount factor for the same period is e
−rt
. Thus a cash
fl ow C
t
occurring in year t and discounted at continuously compounded
rate r will be worth C
t
e
−rt
today, as follows:
