Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

8 Chapter 1

A growing annuity pays out a sum C that grows at a periodic growth

rate g. If the annuity is ﬁ nite, its value today is given by

PV of ﬁ nite growing annuity

−

()

...

()

⎛

⎝

⎞

⎠

⎡

⎣

⎢

⎤

⎦

⎥

−

CBA

Periodic payment, C 1,000

Number of future periods paid, n 5

Discount rate, r 12%

Present value of annuity

Using formula 3,604.78 <-- =B2*(1-1/(1+B4)^B3)/B4

Using Excel's

function

3,604.78 <-- =PV(B4,B3,-B2)

Period

Annuity

payment

1 1,000.00 <-- =B2

2 1,000.00

3 1,000.00

4 1,000.00

5 1,000.00

Present value using Excel's

function

3,604.78 <-- =NPV(B4,B10:B14)

COMPUTING THE VALUE OF A FINITE ANNUITY

If the annuity promises an inﬁ nite series of constant future payments,

then this formula reduces to

PV of inﬁ nite annuity

r11

()

...

CBA

Periodic payment, C 1,000

Discount rate, r 12%

Present value of annuity 8,333.33 <-- =B2/B3

COMPUTING THE VALUE OF AN INFINITE ANNUITY

9 Basic Financial Calculations

CBA

First payment, C 1,000

Growth rate of payments, g 6%

Number of future periods paid, n 5

Discount rate, r 12%

Present value of annuity

Using formula 4,010.91 <-- =B2*(1-((1+B3)/(1+B5))^B4)/(B5-B3)

Period

Annuity

payment

1 1,000.00 <-- =B2

2 1,060.00 <-- =$B$2*(1+$B$3)^(A11-1)

3 1,123.60 <-- =$B$2*(1+$B$3)^(A12-1)

4 1,191.02 <-- =$B$2*(1+$B$3)^(A13-1)

5 1,262.48 <-- =$B$2*(1+$B$3)^(A14-1)

Present value using Excel's NP

V function

4,010.91 <-- =NPV(B5,B10:B14)

COMPUTING THE VALUE OF A GROWING FINITE ANNUITY

Taking the previous formula and letting n → ∞, we can compute the

value of an inﬁ nite growing annuity:

PV of inﬁ nite growing annuity

−

()

...

, provided

Here is an illustration in Excel:

This formula can easily be implemented in Excel, and—as shown here—

can also be computed using the Excel NPV function:

CBA

Periodic payment, C 1,000 <-- Starting at date 1

Growth rate of payments, g 6%

Discount rate, r 12%

Present value of annuity 16,666.67 <-- =B2/(B4-B3)

COMPUTING THE VALUE OF A GROWING INFINITE ANNUITY

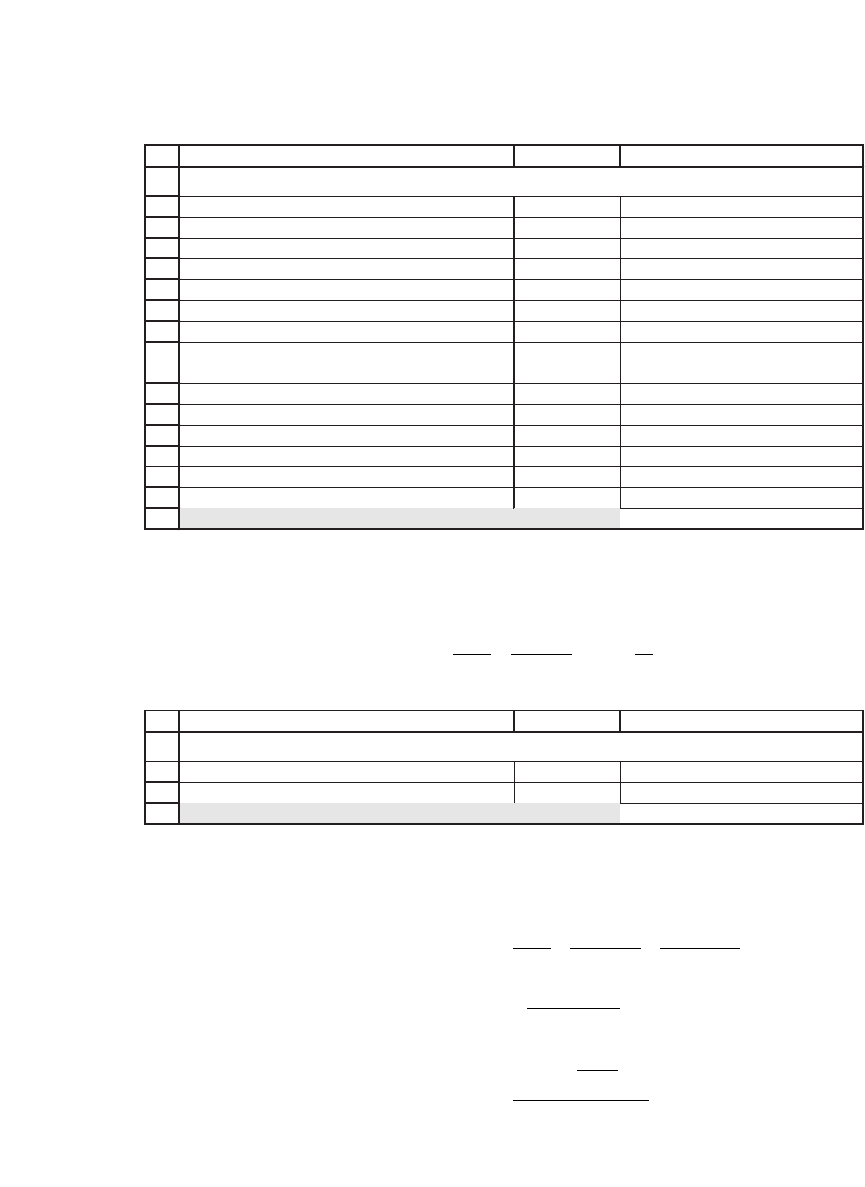
1.3 Internal Rate of Return and Loan Tables

The internal rate of return (IRR) is deﬁ ned as the compound rate of

return r that makes the NPV equal to zero:

∑

()

10 Chapter 1

To illustrate, consider the following example given in rows 2–10. A project

costing 800 in year zero returns a variable series of cash ﬂ ows at the end

of years 1–5. The IRR of the project (cell B10) is 22.16 percent.

By playing with the discount rate or by using Excel’s Goal Seek, we

can determine that at 22.16 percent the NPV in cell B12 is zero.

ABC

Year Cash flow

0 -800

1 200

2 250

3 300

4 350

5 400

Internal rate of return 22.16% <-- =IRR(B3:B8)

INTERNAL RATE OF RETURN

AB C

Discount rate 12%

Year Cash flow

0-800

1200

2250

3300

4350

5400

Net present value (NPV) 240.81 <-- =B5+NPV(B2,B6:B10)

INTERNAL RATE OF RETURN

Note that the Excel IRR function includes as arguments all the cash

ﬂ ows of the investment, including the ﬁ rst—in this case negative—cash

ﬂ ow of −800.

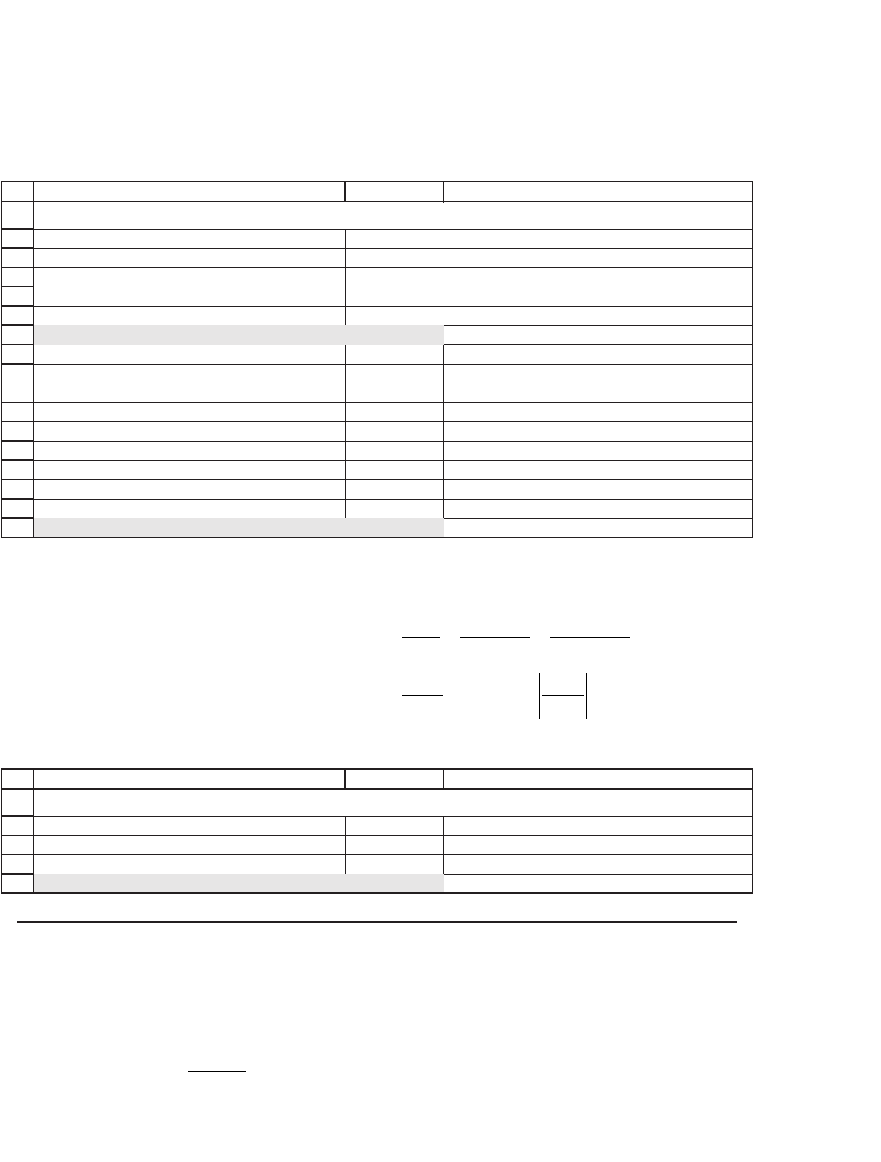
1.3.1 Determining the IRR by Trial and Error

There is no simple formula to compute the IRR. Excel’s IRR function

uses trial and error, which can be simulated as shown in the following

spreadsheet:

11 Basic Financial Calculations

Here’s the way the Goal Seek screen looked before we got the correct

answer:

AB C

Discount rate 22.16%

Year Cash flow

0-800

1200

2250

3300

4350

5400

Net present value (NPV) 0.00 <-- =B5+NPV(B2,B6:B10)

INTERNAL RATE OF RETURN

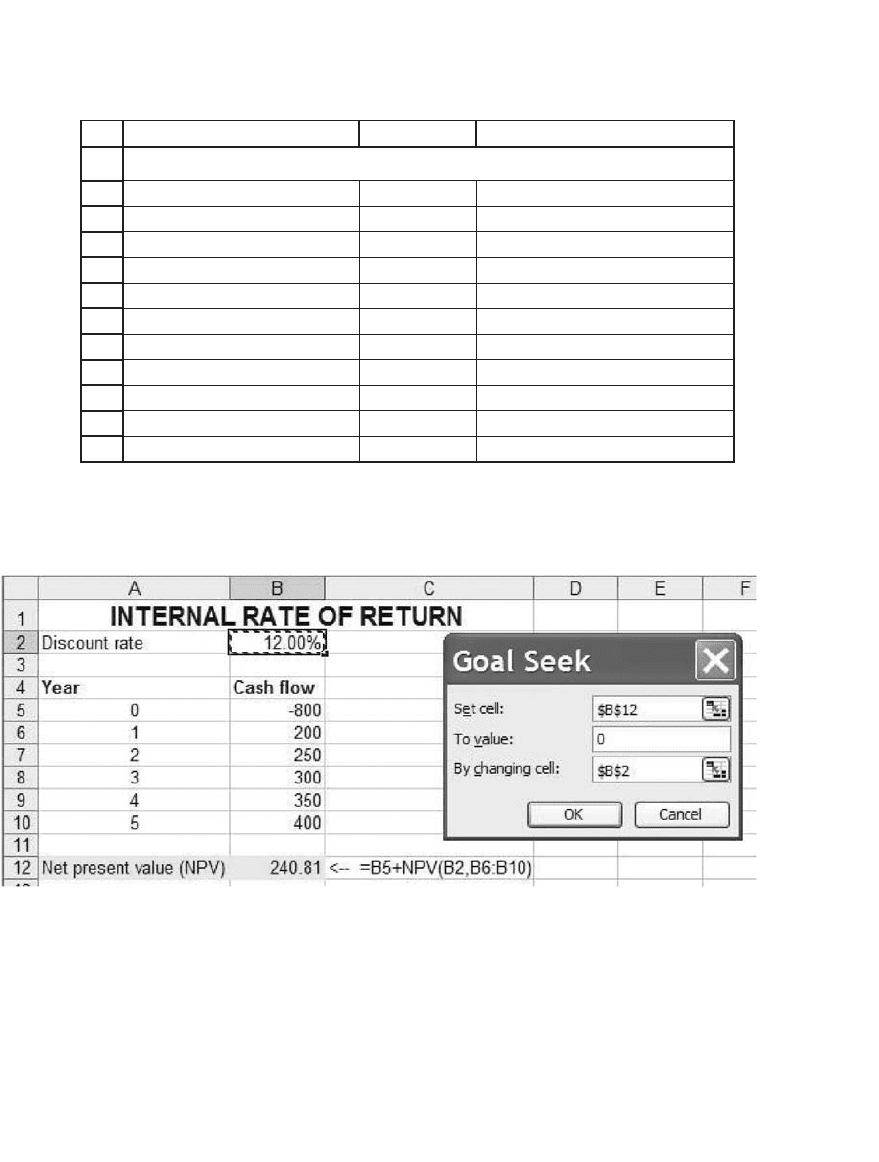
1.3.2 Loan Tables and the Internal Rate of Return

The IRR is the compound rate of return paid by the investment. To under-

stand this point fully, it helps to make a loan table, which shows the

division of the investment’s cash ﬂ ows between investment income and

the return of the investment principal:

12 Chapter 1

AB CDE

Year

Cash flow

-800

2100

2250

3300

3450

4500

Internal rate of return 22.16% <-- =IRR(B3:B8)

USING THE IRR IN A LOAN TABLE

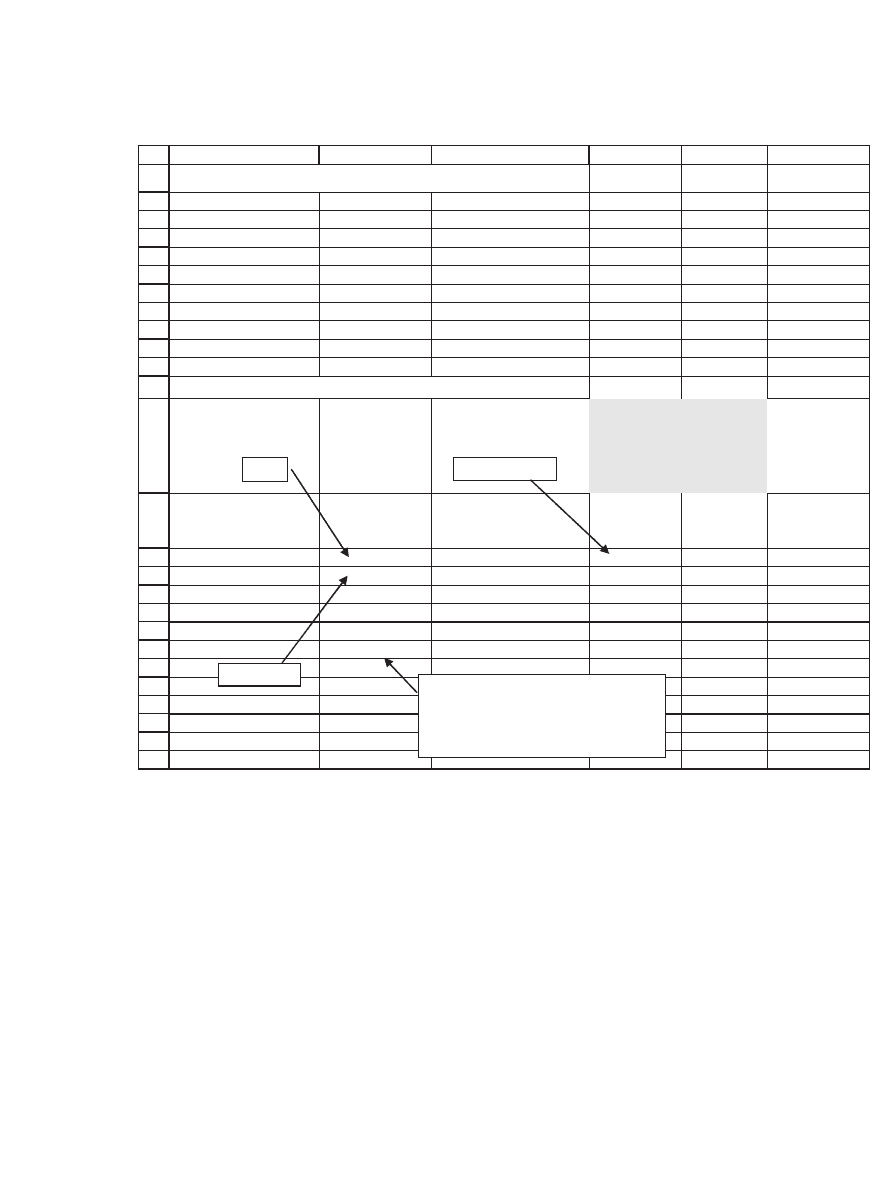
Year

Investment at

beginning of

year

Cash flow

at end of year

Income

Return of

principal

1 800.00 200.00 177.28 22.72 <-- =C15-D15

2 777.28 250.00 172.25 77.75

3 699.53 300.00 155.02 144.98

4 554.55 350.00 122.89 227.11

5 327.44 400.00 72.56 327.44

60.00

INTERNAL RATE OF RETURN

Division of cash flow

between investment

income and return of

principal

=-B3

=B15-E15

=$B$10*B15

The remaining investment principal

in the year after the last cash flow is

zero, indicating that all the principal

has been repaid.

The loan table divides each of the cash ﬂ ows of the asset into an

income component and a return-of-principal component. The income

component at the end of each year is IRR times the principal balance at

the beginning of that year. Notice that the principal at the beginning of

the last year ($327.44 in the example) exactly equals the return of prin-

cipal at the end of that year.

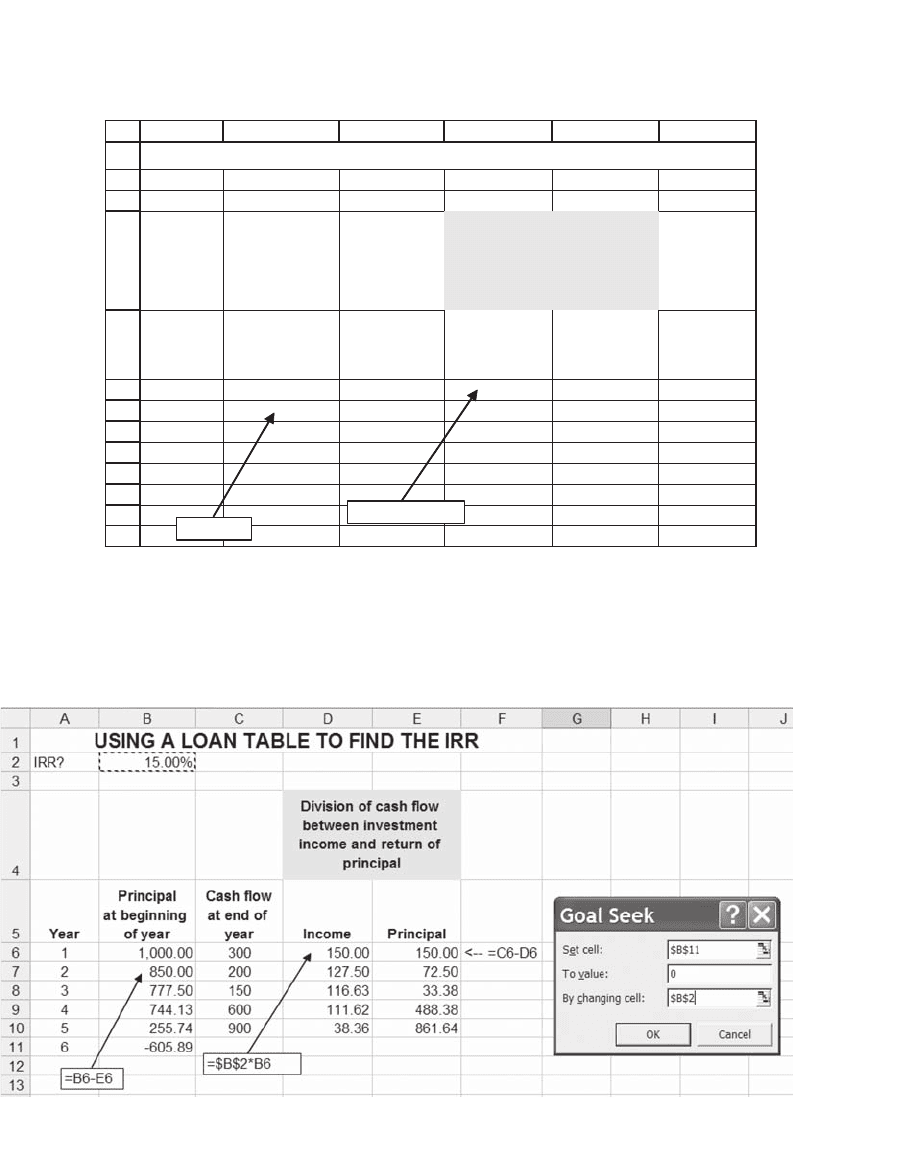
We can actually use the loan table to ﬁ nd the internal rate of return.

Consider an investment costing $1,000 today that pays off the cash ﬂ ows

indicated at the end of years 1, 2, 5. At a rate of 15 percent (cell B2), the

principal at the beginning of year 6 is negative, indicating that too little

has been paid out in income. Thus the IRR must be larger than 15

percent.

13 Basic Financial Calculations

AB C D E F

IRR? 15.00%

Year

Principal

at beginning

of year

Cash flow

at end of

year Income Principal

1 1,000.00 300 150.00 150.00 <-- =C6-D6

2 850.00 200 127.50 72.50

3 777.50 150 116.63 33.38

4 744.13 600 111.62 488.38

5 255.74 900 38.36 861.64

6 -605.89

USING A LOAN TABLE TO FIND THE IRR

Division of cash flow

between investment

income and return of

principal

=$B$2*B6

=B6-E6

If the interest rate in cell B2 is indeed the IRR, then cell B11 should be

0. We can use Excel’s Goal Seek (found on the Tools menu) to calculate

the IRR:

14 Chapter 1

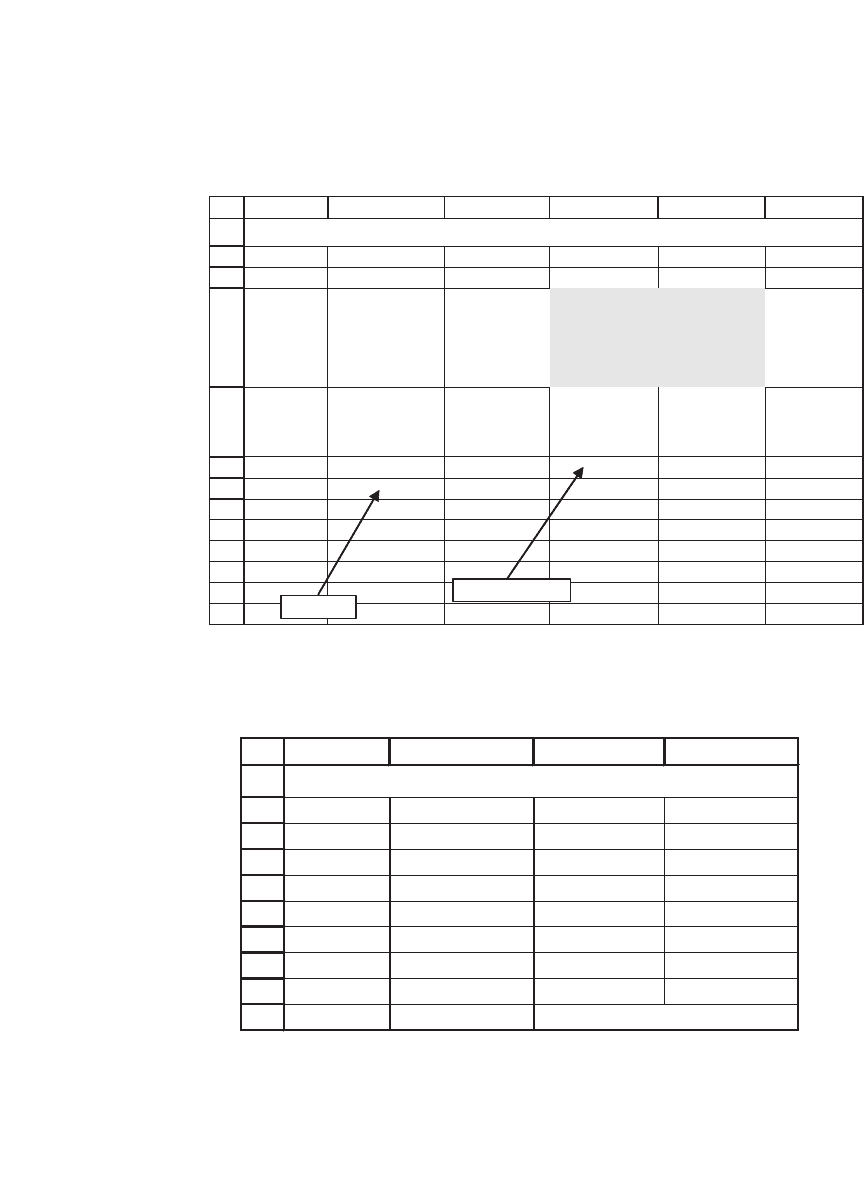
As shown here, the IRR is 24.44 percent:

AB C D E F

IRR? 24.44%

Year

Principal

at beginning

of year

Cash flow

at end of

year Income Principal

1 1,000.00 300 244.36 55.64 <-- =C6-D6

2 944.36 200 230.76 -30.76

3 975.13 150 238.28 -88.28

4 1,063.41 600 259.86 340.14

5 723.26 900 176.74 723.26

6 0.00

USING A LOAN TABLE TO FIND THE IRR

Division of cash flow

between investment

income and return of

principal

=$B$2*B6

=B6-E6

Of course, we could have simpliﬁ ed life by just using the IRR

function:

AB C D

Year Cash flow

0 -1,000

1300

2200

3150

4600

5900

IRR 24.44% <-- =IRR(B17:B22)

Direct calculation of IRR

15 Basic Financial Calculations

AB C

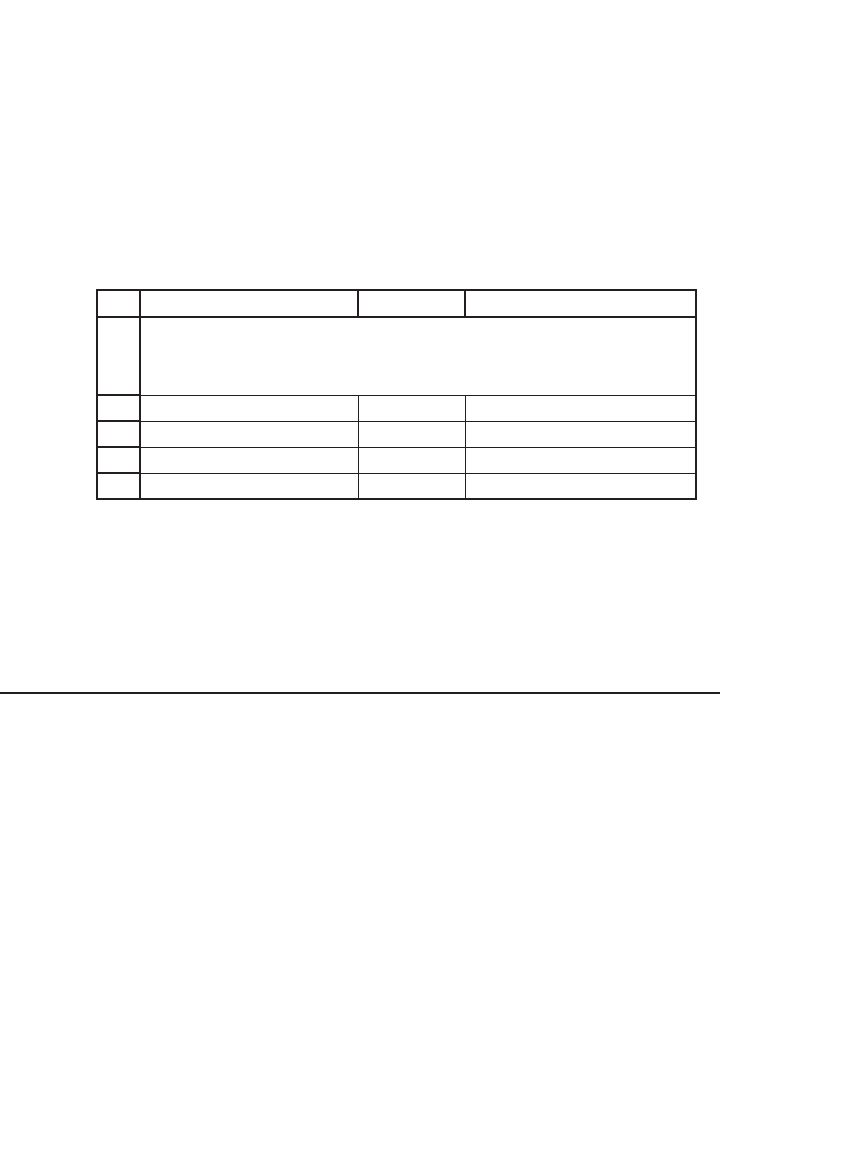
Initial investment 1,000

Periodic cash flow 100

Number of payments 30

IRR 9.307% <-- =RATE(B4,B3,-B2)

USING EXCEL'S RATE FUNCTION TO

COMPUTE THE IRR

1.3.3 Excel’s Rate Function

Excel’s Rate function computes the IRR of a series of constant future

payments. In the following example, we pay $1,000 today for an annual

payment of $100 for the next 30 years. Rate shows that the IRR is 9.307

percent:

Note: Rate works much like PMT and PV, discussed elsewhere in this

chapter; it requires a sign change between the initial investment and the

periodic cash ﬂ ow (note that we have used −B2 in cell B5). It also has

switches to allow for payments that start today and payments that start

one period from now (not shown in the example).

1.4 Multiple Internal Rates of Return

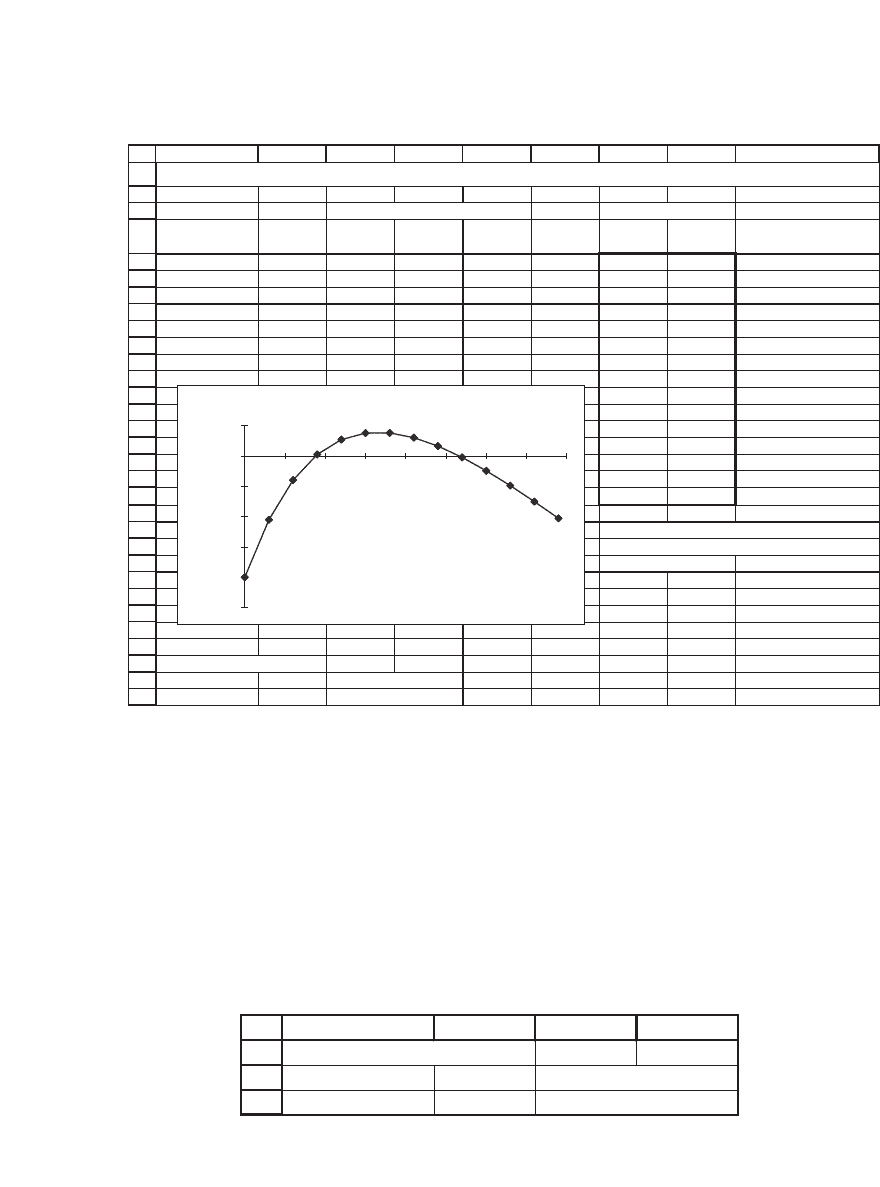
Sometimes a series of cash ﬂ ows has more than one IRR. In the next

example we can tell that the cash ﬂ ows in cells B6 : B11 have two IRRs,

since the NPV graph crosses the x-axis twice:

16 Chapter 1

Excel’s IRR function allows us to add an extra argument that will

help us ﬁ nd both IRRs. Instead of writing =IRR(B6 : B11), we write

=IRR(B6 : B11,guess). The argument guess is a starting point for the

algorithm that Excel uses to ﬁ nd the IRR; by adjusting the guess, we can

identify both the IRRs. Cells B30 and B31 give an illustration.

There are two things to note about this procedure:

•

The argument guess merely has to be close to the IRR; it is not unique.

For example by setting the guesses equal to 0.1 and 0.5, we will still get

the same IRRs:

ABCD

Identifying the two IRRs

First IRR 8.78% <-- =IRR(B6:B11,0.1)

Second IRR 26.65% <-- =IRR(B6:B11,0.5)

ABCDEFGH I

Discount rate 6%

NPV -3.99 <-- =NPV(B2,B7:B11)+B6

DATA TABLE

Discount

rate

NPV

Year Cash flow

-3.99 Table header, <-- =B3

0-145 0%-20.00

1100 3%-10.51

2100 6%-3.99

3 100 9% 0.24

4 100 12% 2.69

5 -275 15% 3.77

18% 3.80

21% 3.02

24% 1.62

27% -0.24

30% -2.44

33% -4.90

36% -7.53

39% -10.27

Note

: For a discussion of how

to create data tables in Excel

see Chapter 30.

Identifying the two IRRs

First IRR 8.78% <-- =IRR(B6:B11,0)

Second IRR 26.65% <-- =IRR(B6:B11,0.3)

MULTIPLE INTERNAL RATES OF RETURN

Two IRRs

-25.00

-20.00

-15.00

-10.00

-5.00

0.00

5.00

0% 5% 10% 15% 20% 25% 30% 35% 40%

Discount rate

Net present value

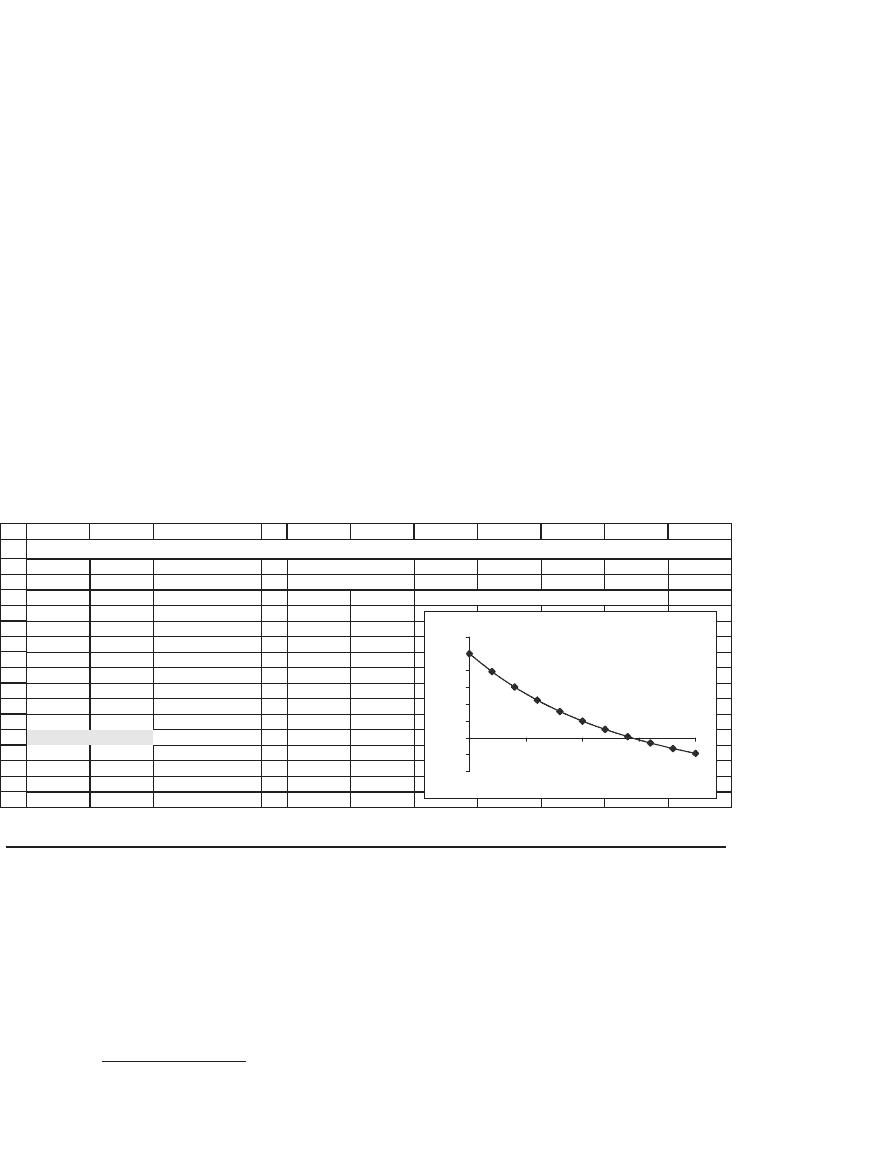
17 Basic Financial Calculations

•

In order to identify the number and the approximate value of the IRRs,

it helps greatly to graph (as we did above) the NPV of the investment

as a function of various discount rates. The internal rates of return are

then the points where the graph crosses the x-axis, and the approximate

location of these points should be used as the guesses in the IRR

function.

From a purely technical point of view, a set of cash ﬂ ows can have

multiple IRRs only if it has at least two changes of sign. Many “typical”

cash ﬂ ows have only one change of sign. Consider, for example, the cash

ﬂ ows from purchasing a bond having a 10 percent coupon, a face value

of $1,000, and eight more years to maturity. If the current market price

of the bond is $800, then the stream of cash ﬂ ows changes signs only once

(from negative in year 0 to positive in years 1–8). Thus there is only one

IRR:

4. If you don’t put in a guess (as we did in the example), Excel defaults to a guess of 0.

Thus, in this case, IRR(B6 : B11) will return 8.78 percent.

1.5 Flat Payment Schedules

Another common problem is to compute a “ﬂ at” repayment for a loan.

For example, you take a loan for $10,000 at an interest rate of 7 percent

per year. The bank wants you to make a series of payments that will pay

off the loan and the interest over six years. We can use Excel’s PMT

function to determine how much each annual payment should be:

AB C DEFGH I JK

ear Cash flow

Data table:

Effect of

0 -800 discount rate on NPV

1 100 1,000.00 <-- =NPV(E4,B4:B11)+B3, table header

2 100 0% 1,000.00

3 100 2% 786.04

4 100 4% 603.96

5 100 6% 448.39

6 100 8% 314.93

7 100 10% 200.00

8 1100 12% 100.65

14% 14.45

IRR 14.36% <-- =IRR(B3:B11) 16% -60.62

18% -126.21

20% -183.72

BOND CASH FLOWS: NPV CROSSES x-AXIS ONLY ONCE, SO THERE IS ONLY ONE IRR

NPV of Bond Cash Flows

-400

-200

200

400

600

800

1000

1200

0% 5% 10% 15% 20%

Discount rate

NPV