Simon Benninga. Financial Modelling 3-rd edition

Подождите немного. Документ загружается.

98 Chapter 2

5. Clicking on Historical Prices accesses a page from which prices and

dividend data may be downloaded. In this case we have asked to see

10 years of monthly price information for GM.

99 Calculating the Cost of Capital

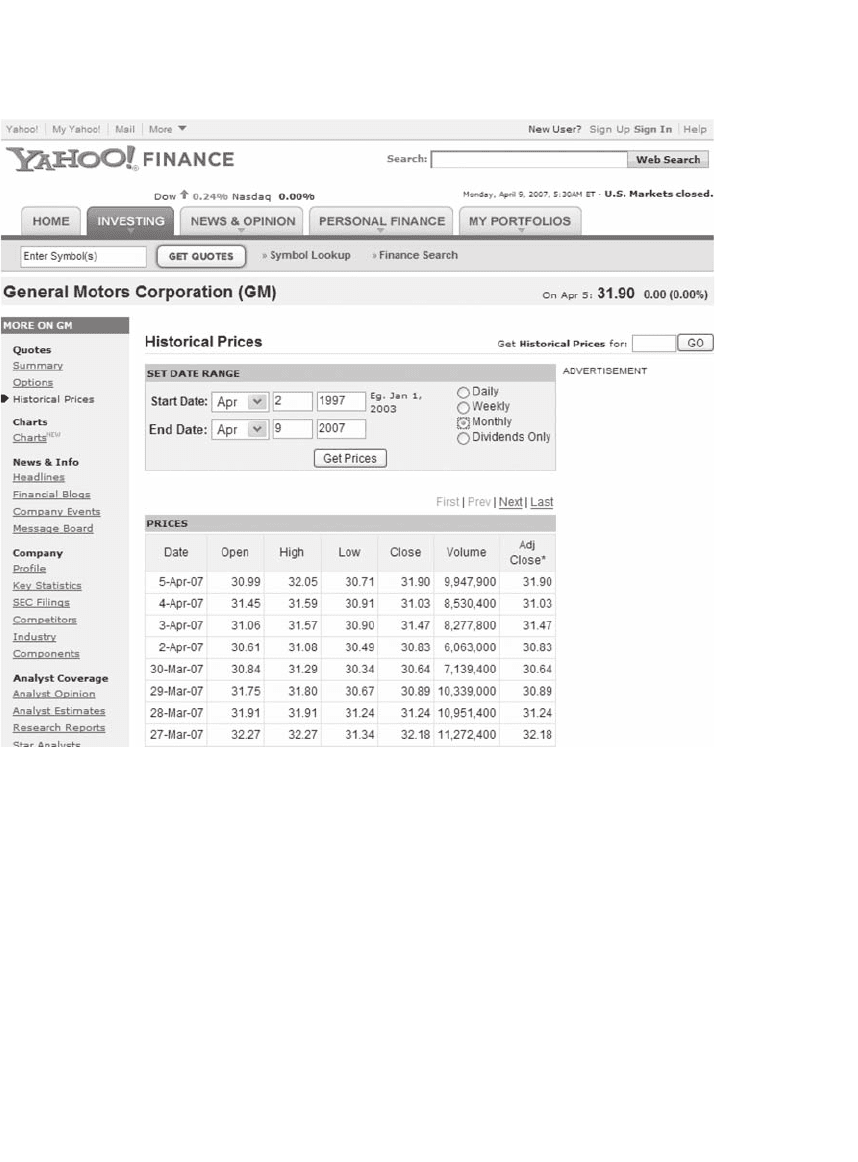
When we click on GetPrices, Yahoo shows us price and dividend infor-

mation for the period requested. The Adjusted Close is the stock price

adjusted for stock splits and dividends:

100 Chapter 2

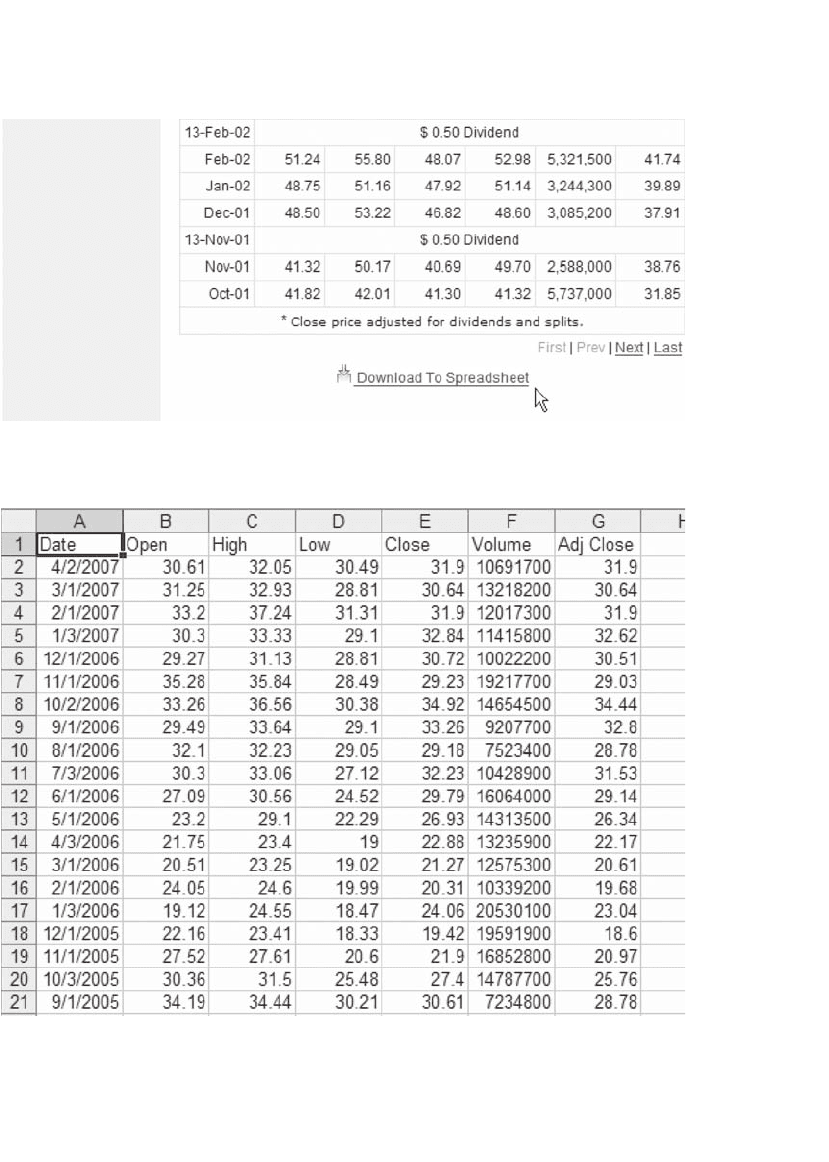
6. Clicking on Download to Spreadsheet gives the data (already adjusted

for dividends and splits) in a ﬁ le that can be opened with Excel.

101 Calculating the Cost of Capital

Here’s the way this ﬁ le looks:

7. Final note: The ticker symbols for two commonly used indexes are

^GSPC (S&P 500) and ^DJI (Dow-Jones 30 Industrials).

Financial Statement Modeling

3.1 Overview

The usefulness of ﬁ nancial-statement projections for corporate ﬁ nancial

management is undisputed. Such projections, termed pro forma ﬁ nancial

statements, are the bread and butter of much corporate ﬁ nancial analysis.

In this and the next chapter we will focus of the use of pro formas for

valuing the ﬁ rm and its component securities, but pro formas also form

the basis for many credit analyses; by examining pro forma ﬁ nancial

statements we can predict how much ﬁ nancing a ﬁ rm will need in future

years. We can play the usual “what if” games of simulation models, and

we can use pro formas to ask what strains on the ﬁ rm may be caused by

changes in ﬁ nancial and sales parameters.

In this chapter we present a variety of ﬁ nancial models. All the models

are sales driven, in that they assume that many of the balance-sheet and

income-statement items are directly or indirectly related to sales. The

mathematical structure of solving the models involves ﬁ nding the solu-

tion to a set of simultaneous linear equations predicting both the balance

sheets and the income statements for the coming years. However, the

user of a spreadsheet need never worry about the solution of the model;

the fact that spreadsheets can solve—by iteration—the ﬁ nancial rela-

tions of the model means that we only have to worry about correctly

stating the relevant accounting relations in our Excel model.

3.2 How Financial Models Work: Theory and an Initial Example

Almost all ﬁ nancial-statement models are sales driven; this term means

that as many as possible of the most important ﬁ nancial statement vari-

ables are assumed to be functions of the sales level of the ﬁ rm. For

example, accounts receivable are often taken as a direct percentage of

the sales of the ﬁ rm. A slightly more complicated example might postu-

late that the ﬁ xed assets (or some other account) are a step function of

the level of sales:

1. The mathematics of balance-sheet spreadsheets involve an iterative method for solving

simultaneous equations known as the Gauss-Seidel method. Although you do not need

to know this method to understand the contents of this chapter, it may be interesting

to know that Gauss-Seidel can be implemented directly in Excel. For details, see

Chapter 32.

104 Chapter 3

Fixed assets

if Sales

etc.

→<

→≤ <

⎧

⎨

⎪

⎩

⎪

bA B

In order to solve a ﬁ nancial-planning model, we must distinguish between

those ﬁ nancial-statement items that are functional relationships of sales

and perhaps of other ﬁ nancial-statement items and those items that

involve policy decisions. The asset side of the balance sheet is usually

assumed to be dependent only on functional relationships. The current lia-

bilities may also be taken to involve functional relationships only, leaving

the mix between long-term debt and equity as a policy decision.

A simple example is the following. We wish to predict the ﬁ nancial

statements for a ﬁ rm whose current balance sheet and income statement

are as follows:

Year 0

Income statement

Sales 1,000

Costs of goods sold (500)

Interest payments on debt (32)

Interest earned on cash and marketable securities 6

Depreciation (100)

Profit before tax 374

Taxes (150)

Profit after tax 225

Dividends (90)

Retained earnings 135

Balance sheet

Cash and marketable securities 80

Current assets 150

Fixed assets

At cost 1,070

Depreciation (300)

Net fixed assets 770

Total assets

1,000

Current liabilities 80

Debt 320

Stock 450

Accumulated retained earnings 150

Total liabilities and equity

1,000

105 Financial Statement Modeling

The current (year 0) level of sales is 1,000. The ﬁ rm expects its sales

to grow at a rate of 10 percent per year, and it anticipates the following

ﬁ nancial-statement relations:

Current assets Assumed to be 15 percent of end-of-year sales

Current liabilities Assumed to be 8 percent of end-of-year sales

Net ﬁ xed assets 77 percent of end-of-year sales

Depreciation 10 percent of the average value of assets on

the books during the year

Fixed assets at cost Sum of net ﬁ xed assets plus accumulated

depreciation

Debt The ﬁ rm neither repays any existing debt nor

borrows any more money over the ﬁ ve-year

horizon of the pro formas

Cash and marketable This is the balance-sheet plug (see the

securities explanation that follows). Average balances of

cash and marketable securities are assumed to

earn 8 percent interest.

3.2.1 The “Plug”

Perhaps the most important ﬁ nancial policy variable in the ﬁ nancial

statement modeling is the “plug”—that is, the balance-sheet item that

will “close” the model:

•

How do we guarantee that assets and liabilities are equal (this is

“closure” in the accounting sense)?

•

How does the ﬁ rm ﬁ nance its incremental investments (this is “ﬁ nan-

cial closure”).

In general the plug in a pro forma model will be one of three ﬁ nancial

balance-sheet items: (1) cash and marketable securities, (2) debt, or (3)

stock.

As an example, consider the balance sheet of our ﬁ rst pro forma

model:

2. We will see in section 3.5.2 that cash and debt are in many senses the same ﬁ nancial

item. Cash can often be considered negative debt and vice versa.

106 Chapter 3

Assets Liabilities and Equity

Cash and marketable

securities

Current liabilities

Current assets Debt

Fixed assets

Fixed assets at cost

—Accumulated

depreciation

Net ﬁ xed assets

Equity

Stock (net funds directly provided by

shareholders)

Accumulated retained earnings (proﬁ ts

not paid out)

Total assets Total liabilities and equity

In the current example we assume that cash and marketable securities

will be the plug. This assumption has two meanings:

1. The mechanical meaning of the plug: Formally, we deﬁ ne

Cash and marketable securities Total liabilities and equit= yy

Current assets Net−−

By using this deﬁ nition, we guarantee that assets and liabilities will

always be equal.

2. The ﬁ nancial meaning of the plug: By deﬁ ning the plug to be cash and

marketable securities, we are also making a statement about how the

ﬁ rm ﬁ nances itself. In our following model, for example, the ﬁ rm sells no

additional stock, does not pay back any of its existing debt, and does not

raise any more debt. This deﬁ nition means that all incremental ﬁ nancing

(if needed) for the ﬁ rm will come from the cash and marketable

securities account; it also means that if the ﬁ rm has additional cash, it

will go into this account.

3.2.2 Projecting Next Year’s Balance Sheet and Income Statement

We have given the ﬁ nancial statement for year 0. We now project the

ﬁ nancial statement for year 1:

3. The cash and marketable securities account can be viewed as a kind of “negative debt.”

We will return to this point later when we use the pro forma model to value the

ﬁ rm.

ﬁ xed assets

107 Financial Statement Modeling

The formulas are mostly obvious. (The dollar signs—indicating that

when the formulas are copied, the cell references to the model parame-

ters should not change—are very important! If you fail to put them in,

the model will not copy correctly when you project years 2 and beyond.)

Model parameters are in boldface in the following list:

BACD

Sales growth 10%

Current assets/Sales 15%

Current liabilities/Sales 8%

Net fixed assets/Sales 77%

Costs of goods sold/Sales 50%

Depreciation rate 10%

Interest rate on debt 10.00%

Interest paid on cash and marketable securities 8.00%

Tax rate 40%

Dividend payout ratio 40%

Year 0 1

Income statement

Sales 1,000 1,100 <-- =B15*(1+$B$2)

Costs of goods sold (500) (550) <-- =-C15*$B$6

Interest payments on debt (32) (32) <-- =-$B$8*(B36+C36)/2

Interest earned on cash and marketable securities 6 9 <-- =$B$9*(B27+C27)/2

Depreciation (100) (117) <-- =-$B$7*(C30+B30)/2

Profit before tax 374 410 <-- =SUM(C15:C19)

Taxes (150) (164) <-- =-C20*$B$10

Profit after tax 225 246 <-- =C21+C20

Dividends (90) 22C*11$B$-= --< )89(

Retained earnings 135 148 <-- =C23+C22

Balance sheet

Cash and marketable securities 80 144 <-- =C39-C28-C32

Current assets 150 3$B$*51C= --< 561

Fixed assets

At cost 1,070 1,264 <-- =C32-C31

Depreciation (300) (417) <-- =B31+C19

Net fixed assets 770 5$B$*51C= --< 748

Total assets 1,000 1,156 <-- =C32+C28+C27

Current liabilities 80 88 <-- =C15*$B$4

Debt 320 320 <-- =B36

Stock 450 450 <-- =B37

Accumulated retained earnings 150 298 <-- =B38+C24

Total liabilities and equity 1,000 1,156 <-- =SUM(C35:C38)

SETTING UP THE FINANCIAL STATEMENT MODEL