Siebertz K., Bebber D., Hochkirchen T. Statistische Versuchsplanung: Design of Experiments (DoE)
Подождите немного. Документ загружается.

6.2 Aufbau und Analyse von Computer-Experimenten 155
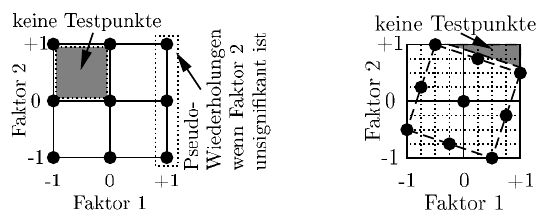
Abb. 6.2a Volllfaktorplan Abb. 6.2b LatinHypercube (LHC)
so verteilt, dass der Raum gleichmäßig ausgefüllt wird. In diesem Zusammenhang
wird von einem Spacefilling Design oder gleichverteiltem Testfeld gesprochen. Im
Vergleich zum Vollfaktorplan fällt der innere Bereich ohne Testpunkte deutlich ge-
ringer aus, so dass hier genauere Vorhersagen für die Ausgangsvariable y in Ab-
hängigkeit der Faktoren getroffen werden können. Zu beachten ist jedoch, dass im
dargestellten Beispiel keine Testpunkte in den Ecken des Faktorraums vorhanden
sind, so dass bei Vorhersagen in diesen Bereichen auf meist ungenaue Extrapolatio-
nen zurückgegriffen werden muss. Pseudo Wiederholungen können im dargestellten
Latin Hypercube nicht auftreten, da jede Faktorstufe jedes Faktors nur ein einziges
Mal verwendet wird.
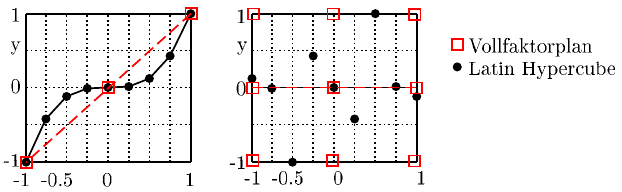
Abbildung 6.3 zeigt die unterschiedliche Datenmenge, die zur Bildung eines Me-
tamodells durch die 9 Testpunkte bei Verwendung der beiden Testfelder zur Verfü-
gung steht. Durch die Berücksichtigung des unsignifikanten Faktors x
2
und die Wahl
des Vollfaktorplans kann nur ein einfaches Modell für den Zusammenhang zwischen
x
1
und y ermittelt werden. Durch die Verwendung des LHCs mit gleicher Anzahl an
Versuchsläufen werden deutlich mehr Informationen über den Zusammenhang zwi-
schen x
1
und y gewonnen. Gerade bei steigender Faktoranzahl werden häufig auch
unsignifikante Faktoren mitberücksichtigt, so dass durch die Verwendung speziell
für Computer-Experimente optimierte Testfelder der Informationsgewinn im Ver-
gleich zu klassischen Testfeldern deutlich gesteigert werden kann. Komplexe Sys-
teme werden somit durch gleichen Versuchsaufwand deutlich genauer dargestellt.
Mittels des Vollfaktorplans wird in diesem Beispiel korrekter Weise kein Effekt
von x
2
ermittelt. Bei Verwendung des LHCs kann je nach verwendetem Auswerte-
algorithmus ein geringer Einfluss von x
2
auf y ermittelt werden. Dieser wird jedoch
im Verhältnis zum Effekt von x
1
unsignifikant bleiben. Im Vergleich zum Informa-
tionsgewinn für signifikante Faktoren (hier x
1
) ist dieses akzeptabel.
Eine Verwendung der speziell für Computer-Experimente entwickelten Testfel-
der in physikalischen Experimenten ist zwar denkbar, die praktische Umsetzbar-
keit ist jedoch häufig mit unverhältnismäßig großem Aufwand verbunden. Weiter-
hin muss bei Verwendung für physikalische Experimente auf Versuchsstreuungen
besonderes Augenmerk gelegt werden.
156 6 Computer-Experiment
x
1
x
2
x
1
x
2
Abb. 6.3 Fallbeispiel zur Verwendung eines Vollfaktorplans oder LHCs
6.2.3 Metamodelle
Basierend auf den Daten des durchgeführten Computer-Experiments wird ein Me-
tamodell erzeugt, welches mit ausreichender Genauigkeit und minimaler Rechen-
zeit das komplexe Simulationsmodell beziehungsweise das zu analysierende Sys-
tem approximiert. Durch die speziell auf Computer-Experimente zugeschnittenen
Testfelder sind optimale Informationen zur Erzeugung des Metamodells gegeben
und sollten im Weiteren vollständig ausgenutzt werden. Im Vergleich zu physikali-
schen Experimenten sollen durch Computer-Experimente meist komplexe Zusam-
menhänge erfasst werden, die vor der Analyse nicht oder nur teilweise bekannt sind.
Daher werden Verfahren zur Metamodellerstellung benötigt, die sich flexibel und
selbständig (ohne Vorgabe von funktionellen Abhängigkeiten zwischen Faktoren
und Ausgangsvariablen des Systems) an komplexe Zusammenhänge anpassen kön-
nen. Verfahren, wie beispielsweise die lineare Regression, welche einen vordefinier-
ten Zusammenhang zwischen Faktoren und Ausgangsvariablen voraussetzen, kön-
nen nur gute Vorhersagemodelle erzeugen, wenn das zu analysierende System den
Annahmen entspricht. Bei komplexen Simulationsmodellen ist der Zusammenhang
zwischen Faktoren und Ausgangsvariablen (Qualitätsmerkmalen) jedoch typischer-
weise nicht bekannt, so dass eine falsche Wahl der Zusammnhänge zu unzureichend
genauen Metamodellen führt. Um dieser Problematik aus dem Wege zu gehen, wer-
den Verfahren wie beispielsweise Neuronale Netze oder Kriging eingesetzt, die sich
selbständig an gegebene Datenpunkte anpassen (Kapitel 8.8 und 8.5).
6.2.4 Analyse und Optimierung
Sind ausreichend genaue Metamodelle mit akzeptablen Rechenzeiten vorhanden,
können verschiedene Analysen in kurzer Zeit durchgeführt werden. Dieses beginnt
mit grafischen Darstellungen, die den Zusammenhang zwischen Faktoren und Aus-
gangsvariable darstellen (Abbildung 6.4a). Neben statischen Grafiken sind durch
schnelle Metamodelle ebenfalls Darstellungen möglich, die direkt nach Verände-
rung von Faktoreinstellungen die neuen Vorhersagen darstellen. Dadurch sind effi-
6.2 Aufbau und Analyse von Computer-Experimenten 157
ziente Hilfsmittel gegeben, die während einer Analyse einen schnellen Einblick und
ein gutes Verständnis für Zusammenhänge zwischen Faktoren und Ausgangsvaria-
blen liefern.
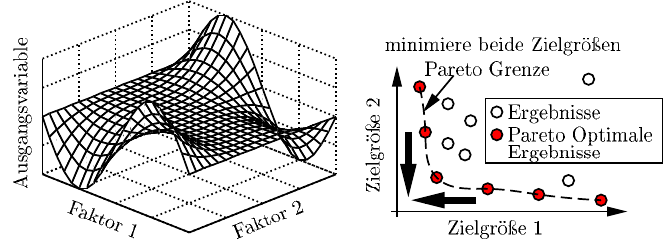
Abb. 6.4a Grafische Darstellung Abb. 6.4b Pareto Grenze
Neben allgemeinen Analysen zum Verständnis des zu analysierenden Systems
werden ebenfalls Optimierungen durchgeführt (Kapitel 9). Hierbei sind meistens
mehrere Zielgrößen zu berücksichtigen, die nicht unabhängig voneinander sind und
widersprechende Ziele verfolgen. Neben klassische Verfahren, die mehrere Zielgrö-
ßen beispielsweise mit Gewichtungsfaktoren zu einer globalen Zielgröße zusam-
menfassen, kommen bei Computer-Experimenten häufig Verfahren zur Bestimmung
der Pareto Grenze zum Einsatz (Abbildung 6.4b). Abbildung 6.4b zeigt beispielhaft
zwei Zielgrößen, die jeweils minimiert werden sollen. Jeder dargestellte Kreis ist
genau ein mögliches Ergebnis, welches durch eine Kombination der Faktoren im
Simulationsmodell erzielt wird. Bei Verwendung eines klassischen Optimierungs-
verfahrens, bei dem beide Zielgößen (Z
1
,Z
2
) zu einer globalen Zielgröße Z
global
zusammengefasst werden (Z
global
= Z
1
w
1
+ Z
2
[1 −w
1
] mit 0 ≤ w
1
≤ 1), ist das Er-
gebnis der Optimierung genau ein Punkt auf der Pareto Grenze. Welcher Punkt auf
der Pareto Grenze gefunden wird, hängt dabei entscheidend von der Kombination
der einzelnen Zielgrößen zur globalen Zielgröße ab. In unserem Beispiel von der
Wahl des Gewichtungsfaktors w
1
. In der Praxis wird dann meistens mit dem ermit-
telten Ergebnis und den dazugehörigen Faktoreinstellungen weiter gearbeitet. Die
Art der Zielgrößenkombination und die Wahl der Gewichtungen ist jedoch mehr
oder weniger subjektiv und willkürlich, wodurch das erzielte Optimum und die da-
zugehörigen Faktoreinstellungen ebenfalls variabel sind. Falls die gefundenen Fak-
toreinstellungen aus einem Grund nicht akzeptabel sind (z.B. hoher Fertigungsauf-
wand oder hohe Kosten der benötigten Bauteile) kann ein weiteres Optimum auf der
Pareto Grenze nur gefunden werden, wenn die Art der Zielgrößenkombination oder
die Gewichtungsfaktoren verändert werden und eine komplett neue Optimierung
durchgeführt wird.
Für jeden Punkt der Pareto Grenze gilt, dass keine Zielgröße verbessert werden
kann ohne eine andere zu verschlechtern. Diese Eigenschaft wird auch als Pareto
Optimal bezeichnet. Ziel einer Optimierung für mehrere Zielgrößen ist es eine Grup-
158 6 Computer-Experiment
pe von pareto optimalen Punkten auf der Pareto Grenze zu finden, die gleichmäßig
auf der gesamten Pareto Grenze verteilt sind. In der Praxis ergibt sich dadurch die
Möglichkeit aus den gefundenen pareto optimalen Lösungen, welche nicht durch
vordefinierte Gewichtungen eingeschränkt wurden, einen sinnvollen Kompromiss
nicht nur zwischen den Zielgrößen zu wählen sondern auch gleichzeitig die dazuge-
hörigen Faktoreinstellungen zu betrachten. In der Praxis zeigt sich, dass sich durch
kleine Verschiebungen auf der Pareto Grenze deutlich bessere Faktoreinstellungen
ergeben können, die zum Beispiel eine einfachere oder kostengünstigere Fertigung
ermöglichen.
Diese und andere Analysen fließen zurück in das zu entwickelnde Produkt oder
in die Verbesserung des Simulationsmodells. Auch wenn heutzutage physikalische
Experimente und Prototypentests meistens nicht verzichtbar sind, wird der Entwick-
lungsprozess durch einen iterativen Einsatz von Computer-Experimenten verkürzt
und das Ergebnis spürbar verbessert. Es zeigt sich gerade bei anschließenden phy-
sikalischen Experimenten, dass der Bereich für das physikalische Experiment auf
enge und sinnvolle Bereiche eingegrenzt werden kann.
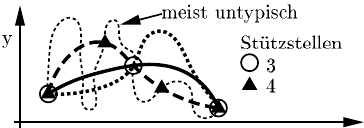
Kapitel 7
Versuchspläne für komplexe Zusammenhänge
7.1 Einleitung
Der Bedarf an Versuchsplänen (Testfelder), die zur Analyse komplexer und nichtli-
nearer Systeme eingesetzt werden, nimmt durch den steigenden Einsatz von Com-
puter-Experimenten (siehe Kapitel 6) während Produktentwicklungen stetig zu. Die
Erhöhung der Faktorstufenanzahl gegenüber klassischen Versuchsplänen für physi-
kalische Experimente ist dabei eine grundlegende Forderung an diese Versuchsplä-
ne. Nur so wird eine umfangreiche Datenbasis geschaffen, die eine Abbildung kom-
plexer Zusammenhänge ermöglicht. Betrachtet wird dazu eine unbekannte Funktion
y = f (x
1
), von der beispielhaft drei Stützstellen bekannt sind (Abbildung 7.1, ’Krei-
se’).
Aus mathematischer Sicht ist durch drei Punkte eine quadratische Funktion aus-
reichend genau definiert. In den meisten Fällen kann jedoch von einem rein quadrati-
schem Zusammenhang nicht ausgegangen werden. Neben der quadratischen Lösung
existieren unendlich viele theoretische Funktionszusammenhänge (Bild 7.1) welche
durch die drei gegebenen Stützstellen verlaufen. In der Praxis zeigt sich, dass in den
häufigsten Fällen zwar von komplexeren Zusammenhängen als linear oder quadra-
tisch ausgegangen werden muss, jedoch hoch komplexe Zusammenhänge, wie in
Bild 7.1 ebenfalls dargestellt, nicht zu erwarten und somit zu vernachlässigen sind.
Eine sinnvolle Vorhersage der zu beschreibenden Zusammenhänge wird durch die
Erhöhung der Stützstellenanzahl (Faktorstufen) erreicht. Im dargestellten Beispiel
ist bereits durch eine vierte Stützstelle (Abbildung 7.1, ’Dreiecke’) die Wahrschein-
Abb. 7.1 Stützstellen zur Bestimmung
einer unbekannten nichtlinearen Funkti-
on
K. Siebertz et al., Statistische Versuchsplanung, VDI-Buch, 159
DOI 10.1007/978-3-642-05493-8_7, © Springer-Verlag Berlin Heidelberg 2010
x
1

160 7 Versuchspläne für komplexe Zusammenhänge
lichkeit, den wahren aber unbekannten Zusammenhang zwischen x
1
und y zu finden,
deutlich erhöht.
Da komplexe nichtlineare Modelle hauptsächlich bei Verwendung von Computer-
Experimenten benötigt werden, können die speziellen deterministischen Eigen-
schaften von Simulationsmodellen, wie keine Versuchsstreuung (siehe Kapitel 6),
zur Konstruktion von Testfeldern Berücksichtigung finden. Bei der Auslegung ei-
nes Vesuchsfelds (Testfelds) für Computer-Experimente wird eine Gruppe von ide-
al verteilten Testpunkten D
n
r
=
{
x
1
,···,x
n
r
}
aus einem Faktorraum der Dimensi-
on n
f
(= Faktoranzahl) gesucht. Zur Vereinfachung der im Weiteren dargestellten
Gleichungen und Herleitungen wird als Basis für den Faktorraum der Einheitsraum
C
n
f
= [0,1]
n
f
verwendet.
Das übergeordnete Ziel für die Wahl der Testpunkteverteilung ist meist eine exak-
te und robuste Vorhersage des globalen Mittelwerts einer zu untersuchenden Funk-
tion y bei Berücksichtigung des gesamten Faktorraums C
n
f
.
1
n
r
n
r
∑
i=1
y(x
i
) =
Z
C
n
f
y (7.1)
7.2 Gütekriterien für Testfelder
Für die Erzeugung von Testfeldern ist entsprechend zu Entwicklungen von techni-
schen Systemen ein Gütekriterium zur Beurteilung der Qualität notwendig. Neben
grundsätzlichen Qualitätskriterien wie Orthogonalität oder Symmetrie wurden ver-
schiedene Qualitätskriterien zur Beurteilung von Testfeldern entwickelt.
Liegen bereits grundlegende Informationen über das zu untersuchende System
(z.B. Simulationsmodell) vor (z.B. Messdaten oder Zusammenhänge zwischen Fak-
toren und Ausgangsvariablen), werden diese in die Konstruktion der Testfelder in-
tegriert, wodurch speziell an die jeweiligen Vorinformationen angepasste Testfelder
entstehen. Eine Verallgemeinerung ist in diesen Fällen durch die Vielzahl an unter-
schiedlichen Vorinformationen nicht möglich, so dass sich die folgenden Erläute-
rungen auf Anwendungen beziehen, bei denen nur geringe oder keine Informatio-
nen vorhanden sind. In diesen Fällen liegt das Augenmerk auf einem gleichmäßigen
und hohen Informationsgewinn im gesamten Faktorraum. In der Praxis zeigt sich,
dass der Einsatz von allgemeinen Feldern in vielen Anwendungen mit vorhandenen
Vorinformationen ebenfalls sinnvoll ist.
7.2.1 MiniMax und MaxiMin
JOHNSON et al. [82] schlägt in seiner Arbeit vor, den minimalen beziehungsweise
maximalen Abstand zwischen allen Testpunkten als Qualitätskriterium zu verwen-
den. Dabei erfüllt eine Abstandsdefinition d (x
1
,x
2
) zweier Testpunkte x
i
folgende

7.2 Gütekriterien für Testfelder 161
Eigenschaften:
d (x
1
,x
2
) ≥ 0
d (x
1
,x
2
) = d (x
2
,x
1
)
d (x
1
,x
2
) ≤ d (x
1
,x
3
) + d (x
3
,x
2
)
mit x
i
∈C
n
f
(7.2)
Diese Eigenschaften werden von der euklidischen Norm d
e
erfüllt, wobei aus Effi-
zienzgründen häufig die Betrachtung des Quadrats d
2
e
vorgezogen wird.
d
e
(x
1
,x
2
) =
v
u
u
t
n
f
∑
j=1
(x
x
1
j
−x
x
2
j
)
2
(7.3)
Sei nun D die Menge aller Abstände zwischen den Testpunkten (x
1
···, x
n
r
) eines
Testfelds T .
D =
{
d(x
i
,x
k
)
}
1 ≤ i < k ≤n
r
(7.4)
Die Verteilung der Testpunkte im Faktorraum C
n
f
wird als gleichmäßig ange-
nommen (space filling), wenn der kleinste Wert von D maximiert wird. Das Ziel des
sogenannten MaxiMin-Kriteriums ist es folglich, den Wert min(D) durch geschickte
Wahl der Testpunkte zu maximieren. Entsprechend wird beim MiniMax-Kriterium
der Maximalwert von D minimiert.
MORRIS et al. [121] hat einige Jahre nach der Veröffentlichung von Johnson
das MaxiMin-Kriterium folgendermaßen erweitert. Die Abstände D werden zuerst
aufsteigend sortiert. Auf Basis der sortierten Abstände werden folgende Kennwerte
ermittelt:
d
1
kleinster Abstand in D
J
1
H
¨
aufigkeit des Abstands d
1
in D
d
2
zweitkleinster Abstand in D
J
2
H
¨
aufigkeit des Abstands d
2
in D
···
(7.5)
Zur Erzeugung des Testfelds werden anschließen folgende Zielgrößen definiert
und nacheinander optimiert.
1a) maximiere d
1
1b) minimiere J
1
2a) maximiere d
2
2b) minimiere J
2
···
(7.6)
Die Verwendung eines einfachen skalaren Kriteriums ist in der Praxis einfacher
als die in Liste 7.6 dargestellten Kriterien, so dass typischerweise das folgende Kri-
terium minimiert wird:
MaxiMin
p
=
"
m
∑
k=1
J
k
d
p
k
#
1/p
(7.7)
162 7 Versuchspläne für komplexe Zusammenhänge
Dabei sind m und p ganzzahlige positive Werte, die vom Anwender zu wählen
sind. Sollen alle Abstände eines Testfelds betrachtet werden, so vereinfacht sich
das MiniMax
p
-Kriterium zu:
MaxiMin
∞
p
=
"
∑
1≤i<k≤n
r
d(x
i
,x
k
)
−p
#
1/p
(7.8)
was eine Sortierung der Abstände in D und die Bestimmung von J
k
überflüssig
macht.
7.2.2 Entropie
SHANNON [166] führte bereits 1948 das Entropie-Kriterium ein, welches die Menge
an Informationen misst, die in einem Datensatz enthalten sind. Sei v(x) die Wahr-
scheinlichkeitsverteilung der Testpunkte im Faktorraum C
n
f
, so ist die Entropie all-
gemein definiert durch [50]:
Ent (x) = −
Z
C
n
f
v(x)log (v (x))dx mit Ent (x) ≥ 0 (7.9)
Für eine mehrdimensionale Normalverteilung v(x) mit n
f
-Dimensionen ist weiter-
hin definiert:
v(x) =
1
π
n
f
2
1
p
|
Cov(x)
|
e
−
1
2
(x−E(x))
0
Cov(x)
−1
(x−E(x))
(7.10)
mit x =
h
x
1
,x
2
,···,x
n
f
i
0
, E (x) =
h
E (x
1
),E (x
2
),···,E
x
n
f
i
0
(7.11)
und Cov(x) =
Cov (x
1
,x
1
) ··· Cov
x
1
,x
n
f
.
.
.
.
.
.
.
.
.
Cov
x
n
f
,x
1
··· Cov
x
n
f
,x
n
f
(7.12)
Wobei E (x
i
) der Erwartungswert des Faktors x
i
und
|
•
|
die Determinante von •
1
ist. Die Entropie ist dann definiert durch [50]:
Ent (x) =
n
f
2
(1 + log(2π)) +
1
2
log(
|
Cov (x)
|
) (7.13)
Eine Maximierung der Entropie entspricht bei konstanter Faktoranzahl n
f
der
Maximierung von log(
|
Cov (x)
|
) beziehungsweise
|
Cov (x)
|
(siehe Kapitel 2.6.1).
1
• ist ein Platzhalter für einen beliebigen Inhalt
7.2 Gütekriterien für Testfelder 163
Bayes’scher Ansatz
Der sogenannte Bayes’sche Ansatz (Bayesian Approach) geht davon aus, dass be-
reits Informationen über ein anzupassendes Modell und des eingesetzten Meta-
modellansatzes vorhanden sind [50]. Aufbauend auf dieser Voraussetzung wird
ein Testfeld gesucht, welches die vorhandene Informationsmenge (gemessen durch
Entropie) am stärksten erhöht. Wird beispielsweise ein Kriging-Modell mit einer
dazugehörigen Korrelationsfunktion r
i j
vorgegeben (Kapitel 8.5), so führt die Ma-
ximierung von log
|
R
|
mit R = [r
i j
] zum optimierten Testfeld [50].
7.2.3 Integrated und Maximum Mean Square Error
Zur Vollständigkeit wird hier das 1989 von SACKS et al. eingeführte Integrated
Mean Square Error (IMSE) Kriterium kurz dargestellt [156]. Sei ˆy (x) = c(x) y
T
ein lineares Vorhersagemodell der Funktion y(x) und y
T
der Ergebnisvektor für ein
gewähltes Testfeld T =
{
x
1
,···,x
n
r
}
. Der Vektor c (x), welcher den Mean Square
Error (MSE) minimiert und gleichzeitig den Erwartungswert E nicht verzerrt, wird
der unverzerrte Prädiktor mit der geringsten Varianz oder auch Best Linear Unbia-
sed Predictor (BLUE) genannt. Dabei ist der MSE definiert durch:
MSE ( ˆy (x)) = E [ ˆy(x) −y (x)]
2
(7.14)
mit E [ ˆy (x)] = E [y (x)] ⇒ unverzerrt (7.15)
Das optimale Testfeld nach dem IMSE-Kriterium minimiert das Integral des
MSE über den gesamten Faktorraum C
n
f
, wobei zusätzlich eine zu definierende
Gewichtungsfunktion G (x) berücksichtigt werden kann.
IMSE =
Z
C
n
f
MSE ( ˆy (x))G (x)dx (7.16)
Ist der Typ des Metamodells ˆy (x) bekannt, für welches mit dem Testfeld Daten
ermittelt werden (z.B. Kriging, Kapitel 8.5), so kann eine Lösung für MSE und IM-
SE in Abhängigkeit des gewählten Modells und der Testpunktverteilung gefunden
werden [156, 92, 50].
Da die Anwendung des IMSE zur Optimierung von Testfeldern aufwendig ist,
wird zur Vereinfachung häufiger der Maximum Mean Square Error eingesetzt [50].
Eine Verringerung des MMSE führt dabei zu besseren Testfeldern.
MMSE = max MSE ( ˆy(x )) (7.17)
164 7 Versuchspläne für komplexe Zusammenhänge
7.2.4 Gleichverteilung (Uniformity)
FANG et al. schlägt zur Beurteilung von Testfeldern verschiedene Kriterien vor, wel-
che die Gleichverteilung (Uniformity) von Testpunkten im Faktorraum beschrei-
ben [44, 189, 95, 48, 100, 45, 47, 50]. Eine Grundvoraussetzung für ein allgemein-
gültiges Gütekriterium ist dabei, dass es unabhängig von Vertauschungen von Fak-
torspalten oder der Versuchsreihenfolge ist. Zwei Testfelder X
1
und X
2
, die durch
Vertauschungen von Spalten oder Zeilen ineinander übergeführt werden können,
müssen daher als gleichwertig beurteilt werden [50].
Diskrepanz
Sei T ein Testfeld mit n
f
Faktoren und n
r
Testläufen sowie z ein beliebiger Punkt
aus dem Faktorraum C
n
f
. N (T,[0,z)) gibt weiterhin die Anzahl aller Testpunkte x
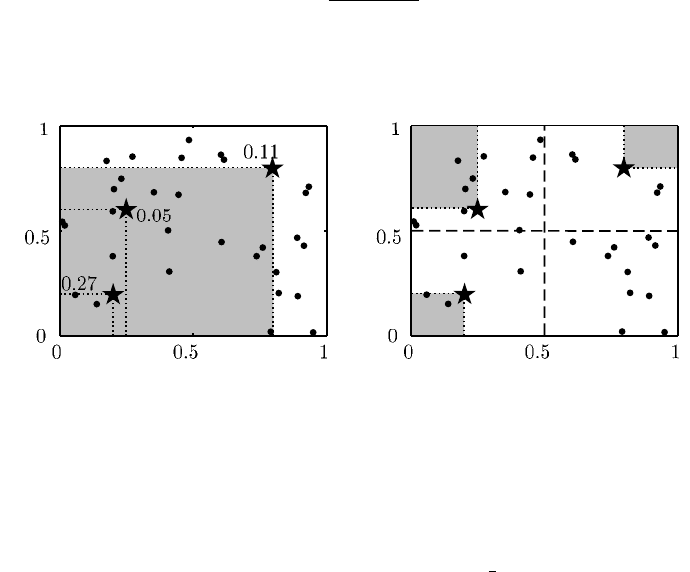
des Testfeldes T an, die in das Rechteck [0, z) fallen (Bild 7.2a). Das Verhältnis
der Anzahl N zur Gesamtanzahl der Testpunkte im Vergleich zum eingeschlossenen
Volumen des n
f
-dimensionalen Rechtecks ergibt die Diskrepanz (discrepancy) des
Punkts z.
Diskrepanz(z) =
N (T,[0,z))
n
r
−Vol ([0,z))
(7.18)
Abbildung 7.2a zeigt beispielhaft drei Diskrepanzen eines Monte-Carlo-Testfelds
mit zwei Faktoren (x
1
,x
2
) und 30 Testpunkten.
Abb. 7.2a Diskrepanz eines zwei-
dimensionalen Monte-Carlo-Testfeldes
Abb. 7.2b Zentrierte L
2
-Diskrepanz
L
p
-Diskrepanz
Der Mittelwert der L
p
Norm der Diskrepanz im gesamten Faktorraum wird Stern
(star)-Diskrepanz genannt und dient als Maß für die Gleichverteilung der Testpunkte
im Faktorraum C
n
f
.
D
p
(T ) =
Z
C
n
f
Diskrepanz(z)
p
1
p
(7.19)
x
1
x
2
z
1
z
2
z
3
x
1
x
2
z
4
z
5
z
6
