Siebertz K., Bebber D., Hochkirchen T. Statistische Versuchsplanung: Design of Experiments (DoE)
Подождите немного. Документ загружается.

3.4 Genauigkeit der Vorhersage 75
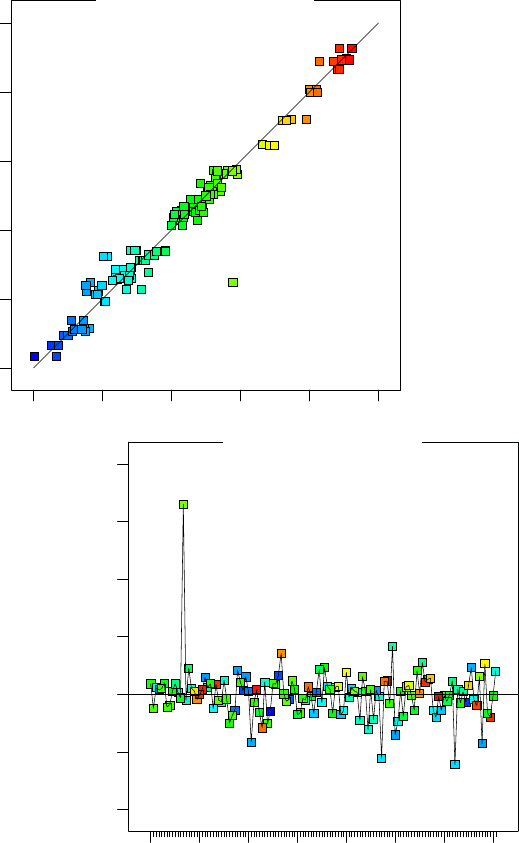
Abb. 3.12 Predicted vs. actu-
al. Hier wird die Vorhersage
über den Testergebnissen auf-
getragen. Die Teststreuung
macht sich bemerkbar. Auch
der Ausreißer fällt auf.
Abb. 3.13 Residual vs. run order. Hier wird die Abweichung zwischen Vorhersage und Testergeb-
nis in der Reihenfolge der Versuche aufgetragen. Der Ausreißer fällt auf und kann eindeutig einem
Versuchslauf zugeordnet werden.
sen. Ausreißer fallen auf, aber zum Beispiel auch ein mitten in der Versuchsreihe
verstellter Versuchsaufbau.
In vielen Fällen ist die Vorhersage im mittleren Bereich der Versuchsergebnis-
se wesentlich besser als bei den niedrigsten oder höchsten Ergebnissen. Diese und
76 3 Kontrollverfahren
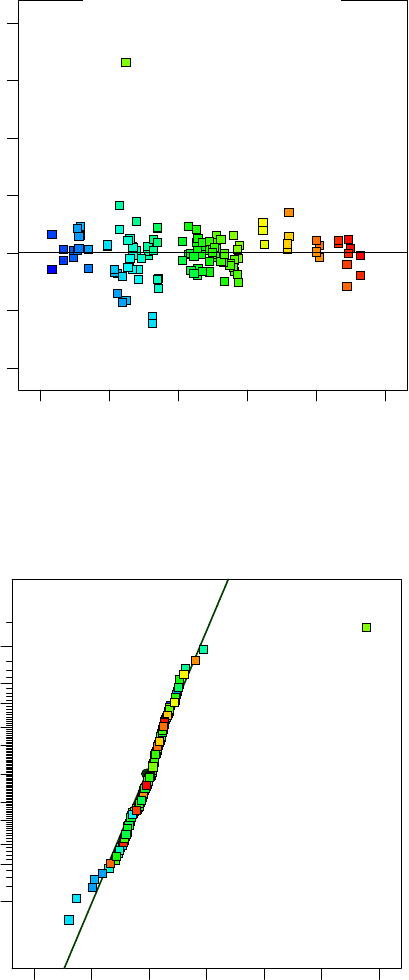
Abb. 3.14 Residual vs. pre-
dicted. Hier werden die Re-
siduen über der Vorhersage
aufgetragen. Ein systema-
tischer Trend würde dabei
auffallen, ist hier jedoch nicht
erkennbar.
andere systematische Ungenauigkeiten zeigt die Darstellung residual vs. predicted.
Die Kombination aus geringer Teststreuung und ungenauem Beschreibungsmodell
fällt hier sehr gut auf, sofern vorhanden.
Abb. 3.15 Full-Normal Plot
der Residuen. Auch hier fällt
der Ausreißer sofort auf, an-
sonsten lässt die Verteilung
der Residuen auf eine zufällige
Streuung schließen.
Rein zufällige Schwankungen folgen der Normalverteilung. Daher liegt es nahe,
den Full-Normal-Plot nicht nur für die Effekte, sondern auch für die Residuen ein-
3.4 Genauigkeit der Vorhersage 77
zusetzen. Jede systematische Abweichung zwischen Vorhersage und Testergebnis
fällt dadurch auf, dass sie nicht mit der Normalverteilung erklärbar ist. Man bildet
also lediglich eine Ausgleichsgerade und findet schnell die potentiellen Ausreißer,
verschiedene Gruppen von Testläufen oder systematische Schwächen des Modells.
Die Diagnose mit Hilfe der Residuen ist in der Regel sehr sicher und erfordert
keine zusätzlichen Versuche. Große Versuchspläne bieten von vornherein mehr Frei-
heitsgrade als kleine Versuchspläne an. Aufwendige Modelle hingegen zehren viele
Freiheitsgrade auf. Das Wechselspiel zwischen Versuchsplan und Beschreibungs-
modell ist letztlich entscheidend. Es geht um eine genaue und reproduzierbare Vor-
hersage des Systemverhaltens, ohne unrealistische Anpassung an streuungsbehafte-
te Versuchswerte.
3.4.3 Löschdiagnosen
3.4.3.1 DFFITS
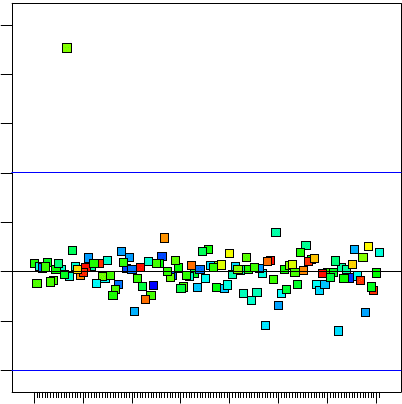
Abb. 3.16 DFFITS-Test. Hier wird die Veränderung der Vorhersage für den Entfall des jeweiligen
Testlaufes eingetragen. Hierzu rechnet die Auswertung eine neue Vorhersage ohne den zu prüfen-
den Lauf und vergleicht diese mit der ursprünglichen Vorhersage. Große Abweichungen sind ein
sicheres Zeichen für Ausreißer. Je nach Versuchsplan sind nicht alle Läufe gleich wichtig für das
Gleichungssystem, was bei dieser Analyse berücksichtigt wird.
Fällt im Residual-Plot ein möglicher Ausreißer auf, so stellt sich sofort die Frage,
wie stark dieser Versuch das gesamte Ergebnis beinflusst. Die Kenngröße DFFITS
78 3 Kontrollverfahren
übernimmt genau diese Prüfung [108, 4] und gehört damit zur Kategorie der Lösch-
diagnosen. Hierzu klappert das Auswerteprogramm alle einzelnen Testwerte ab und
berechnet neue Vorhersagen für die Testwerte, ohne den jeweiligen Testwert bei der
Modellbildung zu berücksichtigen. Die Differenz zwischen der neuen Vorhersage
und der ursprünglichen Vorhersage wird auf die geschätzte Teststreuung (ohne Be-
rücksichtigung des Testwertes i) bezogen und als DFFITS deklariert, difference in
fits. Hierbei gehen auch die jeweiligen Hebelwerte h
ii
ein.
ˆ
σ
−i
ist ein Schätzwert für
die Streuung der gesamten Messreihe, ohne Berücksichtigung der Einzelmessung i.
DFFITS
i
=
ˆy
i
− ˆy
i(−i)
ˆ
σ
(−i)
√
h
ii
(3.10)
3.4.3.2 Cook-Distanz
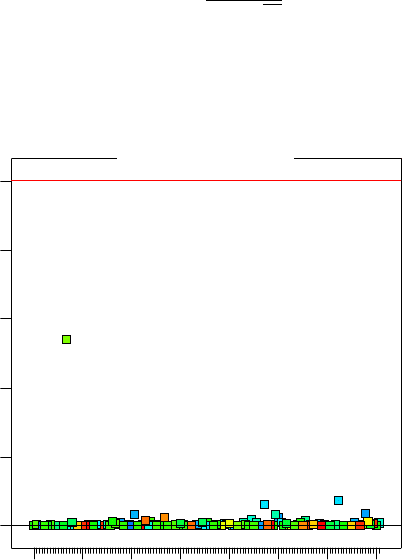
Abb. 3.17 COOK-Test. Die Cook-Distanz gibt Aufschluss darüber, wie stark ein einzelner Wert
die Vorhersage für die gesamte Messreihe beeinflusst.
Auch die Cook-Distanz gehört zu den Löschdiagnosen, allerdings wird hier der
Einfluss auf die Vorhersage aller Ergebnisse ausgewertet. Die Differenz zwischen
den Vorhersagen mit dem Punkt y
i
und ohne den Punkt y
i
wird quadriert, aufsum-
miert und anders normiert als bei der Berechnung des DFFITS. Ausreißer zeichnen
sich dadurch stärker ab. Ab einem Wert von 1 gilt der Ausreißer als kritisch und ver-
fälscht die gesamte Vorhersage. n
m
bezeichnet die Zahl der Modellkonstanten und
ˆ
V die geschätzte Varianz.

3.4 Genauigkeit der Vorhersage 79
D
i
=
∑
n
j=1
ˆy
j
− ˆy
j(−i)
2
n
m
ˆ
V
(3.11)
3.4.4 Box-Cox Transformation
Wenn sich eine starke Abhängigkeit der Residuen von den vorhergesagten Werten
zeigt (residuals vs. predicted) kann die Box-Cox Transformation möglicherweise
Abhilfe schaffen. Eine mathematische Transformation des Qualitätsmerkmals ist
ohne weiteres zulässig, da die Definition des Qualitätsmerkmales selber einer ge-
wissen Willkür unterliegt. Beispielsweise kann man den Kraftstoffverbrauch eines
Fahrzeuges in Litern pro 100 Kilometern angeben oder auch in Miles per Gallon.
Die Nachgiebigkeit von Schraubenfedern lässt sich über einen vorgegebenen Weg
oder eine vorgegebene Kraft messen. Lebensdauerangaben finden über die mittlere
Lebensdauer oder eine Ausfallrate statt, usw. . Die Transformation der Ergebnisgrö-
ße (Qualitätsmerkmal) kann die Abhängigkeit von den Faktoren der Untersuchung
mathematisch günstiger gestalten, was sich über ein genaueres Beschreibungsmo-
dell auszahlt [108, 4].
Glücklicherweise gibt es auch hier ein passendes Instrument, um dem Anwender
zeitraubende Routinearbeit zu ersparen. Der Box-Cox Plot zeigt an, ob sich eine
Transformation lohnt und welche Transformation im speziellen Fall zu den gerings-
ten Residuen führt. Hierzu wird eine allgemein formulierte Funktionsklasse betrach-
tet, die sogenannte Power-Law-Family. Damit ist kein erfolgreicher Familienbetrieb
von Rechtsanwälten gemeint, sondern eine clever formulierte mathematische Trans-
formation, die extrem flexibel ist, aber trotzdem nur von einem Parameter abhängt.
z =
y
λ
,λ 6= 0
ln(y) ,λ = 0
(3.12)
Mit dieser Transformation kann man sehr viele Verläufe realisieren. Bei λ = 1
wird keine Transformation durchgeführt (identische Abbildung), λ = −1 erzeugt
den Kehrwert, λ = 0,5 die Wurzelfunktion und so weiter.
Mit einer passenden Erweiterung konnten Box und Cox die Transformation so
umformen, dass die Ergebniswerte unabhängig von λ in den gleichen Einheiten
erscheinen.
z =
(
y
λ
−1
λ g
λ −1
,λ 6= 0
ln(y)g ,λ = 0
(3.13)
g = (y
1
y
2
...y
n
r
)
1
n
r
(3.14)
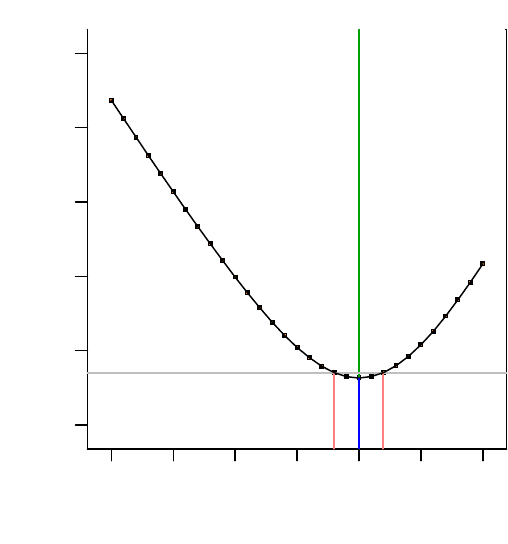
Im Box-Cox Plot wird die Summe der Fehlerquadrate (residual sum of squares)
als Funktion von λ aufgetragen, woraus sich unmittelbar der optimale Wert für λ
ablesen lässt.
80 3 Kontrollverfahren
m
:
Lambda
Ln(ResidualSS)
Box-Cox Plot for Power Transforms
Abb. 3.18 Box-Cox Plot. Für das Fallbeispiel ist offenbar keine Transformation sinnvoll, denn bei
λ = 1 liegt das Minimum der Kurve.
3.4.5 Bestätigungsläufe
Auch wenn die bereits gezeigten Kontrollverfahren das Risiko einer Fehlinterpreta-
tion bereits stark reduzieren, bleibt letztlich immer nur der Bestätigungslauf übrig,
um absolute Gewissheit zu geben. Insbesondere bei Teilfaktorplänen mit dichter
Belegung ist die Chance sehr gering, dass die vorgeschlagene Einstellung bereits
getestet wurde. Es lohnt sich in diesen Fällen immer, logistisch einen Nachversuch
mit der optimierten Einstellung des Systems vorzusehen. Wenn die Möglichkeit be-
steht, sind auch zwei weitere Einstellungen empfehlenswert: Die Einstellung aller
Faktoren auf einen Mittelwert (der sogenannte “center point”) gibt Aufschluss über
auftretende Nichtlinearitäten. Die Wiederholung der ersten Einstellung kann als zu-
sätzlicher Datenpunkt hilfreich sein, um zeitliche Veränderungen aufzudecken, wie
sie zum Beispiel durch Verschleiss oder eine sukzessive Verstellung entstehen.
Kapitel 4
Statistische Modellbildung
4.1 Einleitung
Nachdem wir in den vorigen Kapiteln einen Weg in die Anwendung der statistischen
Versuchsplanung gefunden haben, wird es in der Folge darum gehen, Kapitel 3 auf-
zugreifen und die dort zu findende Darstellung der wesentlichen Kontrollverfahren
zu vertiefen beziehungsweise, wo sinnvoll, zu ergänzen. Es wird dabei um Verfahren
gehen, mit denen sichergestellt wird, dass man
• eine sinnvolle statistische Auswertung durchführt, die es erlaubt, “echte” Effekte
von Effekten zu trennen, die durch das Messrauschen nur vorgetäuscht werden,
• eine dafür sinnvolle Anzahl von Versuchswiederholungen benutzt
• von einem validen Vorhersagemodell ausgeht
• mit der schließlich vorgeschlagenen Systemverbesserung richtig liegt.
Nach einigen Gedanken zur Frage, warum wir uns überhaupt mit Statistik befassen
müssen (keine Panik — es geht...!) werden wir zunächst einige über 80 Jahre alte
Prinzipien bei der statistischen Versuchsplanung kennen lernen: Randomisierung,
Versuchswiederholung und Blockbildung — drei Maßnahmen, die uns helfen wer-
den, das “Signal” vom “Rauschen” zu trennen (Kap. 4.3). Diese Trennung führt uns
zum Thema des statistischen Testens: Was heißt eigentlich “statistisch signifikant”?
Da dieses Thema zwar von zentraler Bedeutung ist, in der Regel aber weder gut er-
klärt noch von Anwendern gut verstanden wird, werden wir den Grundgedanken des
Testens einigen Raum gönnen (Kap. 4.4), bevor wir auf den Kern-Test für geplante
Experimente, die sogenannte Varianzanalyse (Analysis of Variance, ANOVA, vgl.
4.5) zu sprechen kommen. Leider sind alle diese Vorbereitungen nötig, um eine zen-
trale Frage beantworten (und die Antwort verstehen und anwenden) zu können: Wie
viele Versuche muss man eigentlich durchführen, um zu gesicherten, verlässlichen
Ergebnissen zu gelangen (4.5.6)? Last, but not least, müssen wir noch einmal auf
die Residuenanalyse und verwandte Themen zurückkommen: Nur wenn die Voraus-
setzungen der ANOVA erfüllt sind, gelangt man nämlich zu sinnvollen Ergebnissen.
Gilt dies nicht, wird alle “Statistik” zur Makulatur... (vgl. 4.6).
Was aber hat die Auswertung von Versuchen überhaupt mit Statistik zu tun?
K. Siebertz et al., Statistische Versuchsplanung, VDI-Buch, 81
DOI 10.1007/978-3-642-05493-8_4, © Springer-Verlag Berlin Heidelberg 2010

82 4 Statistische Modellbildung
4.2 Warum Statistik?
To call in the statistician after the experiment is done may
be no more than asking him to perform a postmortem
examination: he may be able to say what the experiment
died of.
— Sir Ronald Aylmer Fisher, ca. 1938
1
The truth is that we all live in a non-stationary world;
a world in which external factors never stay still
— George Box, 1989
2
Liegen die Ergebnisse der zuvor geplanten Messreihen vor, kann man sich durch-
aus Situationen vorstellen, wie sie Christer Hellstrand, Statistiker beim Kugellager-
hersteller SKF, 1989 in einem technischen Bericht beschrieben hat: Dort ging es
darum, die Wirkung der Modifikationen dreier Designparameter A, B und C auf
die Lebensdauer bestimmter Kugellager zu ermitteln. Hellstrand ([
66], später auch
George Box, vgl. [14]) beschreibt, wie durch einen simplen Vollfaktorplan mit 2
3
Versuchen eine maßgebliche Interaktion entdeckt wurde, die durch “normale” one
factor at a time-Versuche niemals hätte entdeckt werden können: Während die ein-
zelnen Haupteffekte, wie in Abbildung 4.1 sichtbar wird, eher klein sind, ist der Ein-
fluss der Modifikationen dramatisch, wenn alle drei Modifikationen zugleich durch-
geführt werden. Die bisherige Lebensdauer von 17 Stunden im Falle dreier nicht
modifizierter Parameter konnte durch gleichzeitige Nutzung aller Modifikationen
auf 128 Stunden erhöht werden! Dies ist natürlich ein beachtliches — und später
zu Recht von Box als Beispiel für den Wert der Betrachtung von Interaktionen her-
vorgehobenes — Resultat. An dieser Stelle sei aber auch auf einen weiteren Aspekt
des Ergebnisses hingewiesen: Im Falle derartig klarer und eindeutiger Versuchs-
ergebnisse erübrigt sich im Grunde die Anwendung statistischer Methoden, denn
die Resultate sprechen für sich. Wer würde seinen Chefs keine klare Empfehlung
auf der Basis von Abbildung 4.1 geben?
Leider sind die Ergebnisse der meisten Experimente in der Regel nicht so klar.
Dies liegt natürlich vor allem daran, dass zufällige Streuung der Begleiter einer je-
den Messreihe ist. Sobald jedoch eine Streuung vorliegt, liefern zwei voneinander
unabhängige Versuchsgruppen nicht mehr den gleichen Mittelwert, auch wenn das
System keinerlei systematische Änderung erfahren hat. Bei der Versuchsauswer-
tung entsteht damit die Notwendigkeit, wahre Effekte von scheinbaren Effekten zu
unterscheiden. Während ein wahrer Effekt reproduzierbar ist und die Auswirkung
einer Systemveränderung auf die Systemleistung beschreibt, ist ein “scheinbarer”
1
Den Statistiker hinzuzuziehen, nachdem das Experiment durchgeführt wurde, könnte nicht mehr
bedeuten als ihn um eine Autopsie zu bitten: Er könnte sagen, woran der Versuch gestorben ist.
2
In Wahrheit leben wir alle in einer nicht-stationären Welt; einer Welt, in der externe Faktoren
niemals stillstehen.
4.2 Warum Statistik? 83
17
25
19
21
26
85
16
128
A
B
C
.
.
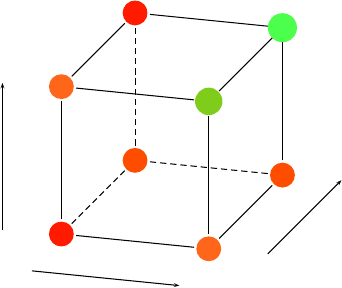
Abb. 4.1 Schematische Darstellung des Einflusses der Designparameter A, B und C: Während die
Veränderung von Parameter A die Lebensdauer von 17 auf 25 Stunden, B auf 19 Stunden und C
auf 26 Stunden erhöhte, wurde festgestellt, dass die gemeinsame Veränderung aller Parameter zu
einer Erhöhung der Lebensdauer des Kugellagers auf 128 Stunden führte!
Effekt das zufällige Produkt der Versuchsstreuung — und daher nicht reproduzier-
bar. Scheinbare Effekte verschlechtern somit die Genauigkeit des Beschreibungs-
modells, denn bei einer Wiederholung der Versuchsreihe nehmen sie andere Werte
an und können sogar ihr Vorzeichen wechseln.
Es geht also darum, “die Spreu vom Weizen zu trennen” — die Quellen unkon-
trollierbarer Variabilität zu enttarnen und deren Effekte möglichst gut zu verstehen.
So stellte sich für den Pionier der Theorie der statistischen Versuchsplanung, R.A.
Fisher, die Frage, ob der bessere Ernteertrag eines mit einem neuen Dünger ge-
düngten Feldes aufgrund der Wirkung des neuen Düngers zu erklären ist — oder
beispielsweise aufgrund einer besseren Bodenbeschaffenheit oder sonnigeren Lage
des ertragreicheren Feldes. Ähnliche Fragen stellen sich natürlich auch in industri-
ellen Anwendungen. Leben wir in einer “stationären” Welt, in der wir die der DoE
zugrunde liegenden Faktoren kontrollieren, alle anderen Parameter aber konstant
halten können?
Mit den Worten von George Box: “To see if you believe in .. stationarity in your
particular kind of work, think of the size of chance differences you expect in mea-
surements taken n steps apart (in time or in space)” — um festzustellen, ob man
an Stationarität in seinem speziellen Arbeitsgebiet glauben kann, denke man an die
Größe von zufälligen Unterschieden, die man n Schritte (zeitlich oder räumlich)
entfernt erwartet... ([15, S.2]).
Die Antwort liegt natürlich auf der Hand: Wir leben in einer nichtstationären
Welt. So basiert beispielsweise jeder Produktionsprozess auf der Einbeziehung von
Menschen und Maschinen. Menschen aber ändern ihr Verhalten mit der Zeit, und
verschiedene Operator werden meist verschiedene Gewohnheiten haben. Maschi-
nen verschleißen, müssen neu eingestellt werden usw. Eingesetzte Materialien kön-
nen sich von Charge zu Charge ändern (müssen und sollten aber nicht)...
84 4 Statistische Modellbildung
Alle diese Faktoren verursachen Variabilität — neben der schon eingangs erwähn-
ten Messungenauigkeit —, und an dieser Stelle kommen Wahrscheinlichkeitsrech-
nung und Statistik zum Einsatz, die mit den Konzepten von “zufälligen Veränder-
lichen” und “Wahrscheinlichkeitsverteilungen” eine universelle Sprache zur Be-
schreibung und Analyse von Variabilität anbieten. Wie groß muss ein Faktoreffekt
sein, um als “signifikant” zu gelten? Wie genau müssen wir messen können, um si-
cher zu sein, dass ein kleiner Effekt “real” ist? Wann sehen wir nur Messrauschen?
Wir benötigen Methoden die uns helfen, zufällige Unterschiede (Pseudo-
Effekte) von systematischen Unterschieden zu trennen.
Aufgrund der Bedeutung dieser Aussage und der vielen in der Praxis auftreten-
den Missverständnisse widmen wir den Grundgedanken statistischen Testens in der
Folge viel Raum. Da wir wie bisher davon ausgehen, dass die meisten Anwender
der statistischen Versuchsplanung Standard-Software zur Durchführung ihrer Be-
rechnungen einsetzen, wird der Fokus dabei allerdings nicht, wie sonst leider allzu
oft, auf der Darstellung der manuellen Rechenschritte liegen, sondern auf einer sorg-
fältigen Darstellung der Grundprinzipien. Anders gesagt: Es soll nicht darum gehen,
wie die Software rechnet, sondern was sie rechnet und wie der jeweilige Output zu
interpretieren ist.
Zuvor sollen jedoch die eng damit zusammenhängenden und seit den Kinder-
tagen der DoE in den zwanziger Jahren des vorigen Jahrhunderts klar definierten
drei Grundprinzipien R.A. Fishers als “Brücke in die Statistik” diskutiert werden
— Randomisierung, Replikation (Wiederholung) und Blockbildung (Kapitel
4.3).
Damit ist der Rahmen abgesteckt, zunächst den zentralen Grundgedanken aller sta-
tistischen Tests zu erläutern (Kapitel 4.4), um anschließend diesen Gedanken auf die
Varianzanalyse, eine ebenfalls bereits durch Fisher eingeführte Prozedur zur Aus-
wertung randomisierter statistischer Versuchspläne zu übertragen (Kapitel 4.5). Erst
mit diesem Instrumentarium wird der Rahmen geschaffen, endgültige, abgesicherte
Aussagen aus den Versuchsergebnissen abzuleiten:
“The statistical approach to experimental design is necessary if we want to draw meaningful
conclusions from data” — der statistische Zugang zur Versuchsplanung ist nötig, wenn wir
sinnvolle Schlussfolgerungen aus den Daten ziehen wollen ([119, S. 11]).
Wenn in diesem Kapitel wiederholt zwei Herren zu Wort kommen, so liegt dies
an deren fundamentaler Bedeutung für die Entwicklung sowohl der statistischen
Versuchsplanung als auch ihrer “Vermarktung” im industriellen Umfeld (diese Aus-
wahl ist, zugegebenermaßen, etwas subjektiv).
Bei Sir Ronald Aylmer Fisher (1890-1962) handelt es sich letztlich um den Er-
finder der DoE, deren Wurzeln mindestens bis ins Jahr 1926 zurückgehen. Fisher
hatte als junger Statistiker an der landwirtschaftlichen Versuchsanstalt Rothams-
ted in England einen äußerst folgenreichen Aufsatz über The Arrangement of Field
Experiments ([55]) — das Arrangieren von Feldexperimenten im wahrsten Sinne
des Wortes — veröffentlicht, in dem alle bis heute gültigen Grundprinzipien der
Versuchsplanung im wesentlichen entwickelt wurden. Fisher, der ab 1933 verschie-
dene Professuren in England innehatte und sich später in Australien niederließ, gilt
als Mitbegründer der gesamten modernen Statistik. Neben mehr als 300 Aufsätzen
