Siebertz K., Bebber D., Hochkirchen T. Statistische Versuchsplanung: Design of Experiments (DoE)

Подождите немного. Документ загружается.

3.3 Beschreibungsmodell 65

0 1 2 3 4 5 6

rel. H.

0 1 2 3 4 5 6

rel. H.

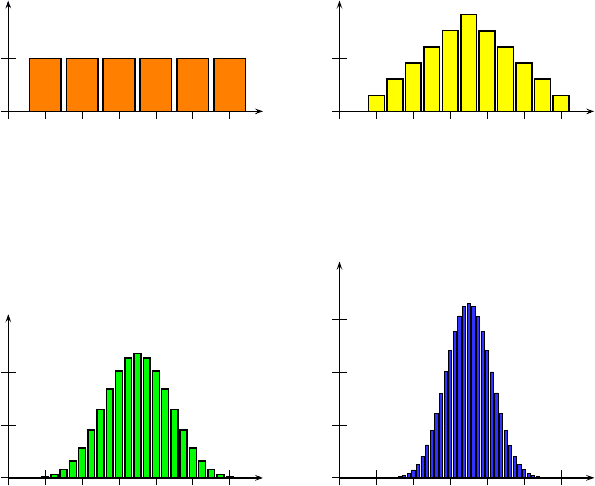
Abb. 3.2 Würfelexperiment mit 48 Millionen Würfen. Auftretenshäuﬁgkeit von Einzelwürfen im

Vergleich zu Mittelwerten aus jeweils zwei Würfen. Der Mittelwert 3,5 kann aus mehreren Kom-

binationen entstehen, ist also im Vergleich zum Mittelwert 1 häuﬁger zu beobachten. Die relative

Häuﬁgkeit bezieht sich auf den arithmetischen Mittelwert der Beobachtungen pro Kategorie.

0 1 2 3 4 5 6

rel. H.

0 1 2 3 4 5 6

rel. H.

Abb. 3.3 Würfelexperiment mit 48 Millionen Würfen. Auftretenshäuﬁgkeit von Mittelwerten

aus jeweils vier und jeweils acht Würfen. Obwohl die Ausgangsverteilung einer nahezu exakten

Gleichverteilung entsprach, ergibt sich bereits bei Gruppen von jeweils acht Würfen eine fast per-

fekte Gaußverteilung der Mittelwerte. Die relative Häuﬁgkeit bezieht sich auf den arithmetischen

Mittelwert der Beobachtungen pro Kategorie.

3.2 und 3.3 ist dies am Beispiel einer Gleichverteilung gezeigt. Ein einziger Wurf

eines Würfels liefert für jede Augenzahl die gleiche Auftretenshäuﬁgkeit. Der Mit-

telwert von acht Würfen hingegen folgt bereits weitgehend einer Gaußverteilung.

Mittlere Werte zwischen 3 und 4 sind in diesem Beispiel sehr viel wahrscheinlicher

als kleine oder große Werte.

Der von Cuthbert DANIEL 1959 entwickelte Half-Normal-Plot nutzt die Gültig-

keit des zentralen Grenzwertsatzes und hat bis heute nicht an Bedeutung verloren.

Ausgehend von einer Normalverteilung der Effekte, erfolgt zunächst die Betragsbil-

dung, dann der Eintrag in eine spezielle Darstellung, das sogenannte Wahrschein-

lichkeitsnetz. Die besondere Konstruktion der Abszisse bewirkt, dass die kumulier-

te Häuﬁgkeitsfunktion einer Normalverteilung als Gerade erscheint. Hierzu werden

die Quantilschritte aufgetragen, also die Flächenschwerpunkte gleichgroßer Teilﬂä-

chen unter der Normalverteilungskurve. Durch die Betragsbildung genügt die Be-

trachtung einer Seite der Kurve und zwar der Seite rechts des Mittelwertes. Die

ﬂächengleichen Stücke kennzeichnen Bereiche gleicher Wahrscheinlichkeit, also

kann man bei einer Normalverteilung davon ausgehen, dass sich diese gleichmä-

ßig auf die abgesteckten Bereiche verteilen. Anders ausgedrückt, wenn alle Effekte

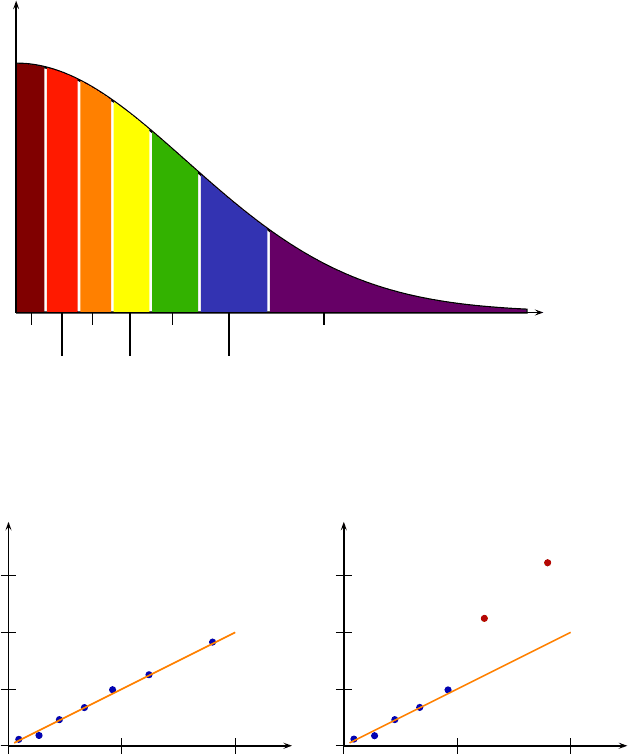
66 3 Kontrollverfahren

0,09

0,27

0,45

0,67

0,92

1,24

1,80

Abb. 3.4 Aufteilung der Normalverteilungskurve in ﬂächengleiche Teilstücke. Die Kurve ist sym-

metrisch, daher genügt die Betrachtung einer Seite. Die Teilstücke kennzeichnen Bereiche gleicher

Auftretenswahrscheinlichkeit. Die Quantilschritte kennzeichnen die jeweiligen Flächenschwer-

punkte der Quantile. Bei einem rein zufälligen Prozess sind die Effektbeträge proportional zu den

Quantilschritten.

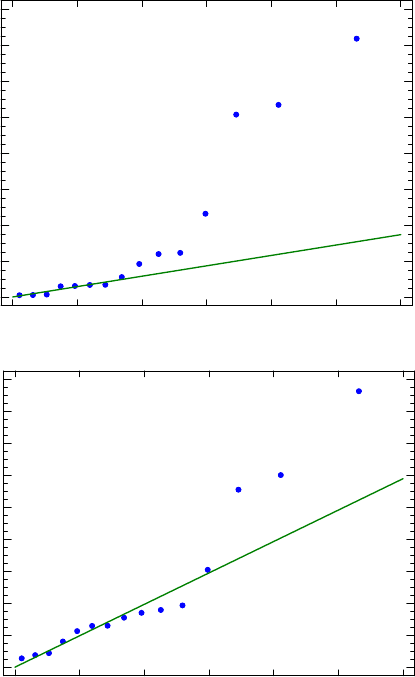
Abb. 3.5 Daniel-Plots für einen Versuchsplan mit acht Versuchsläufen. Scheinbare Effekte sind

reine Zufallsprodukte und daher proportional zu den Quantilschritten. Wahre Effekte lassen sich

nicht durch Zufall erklären, sie sind stärker, liegen also oberhalb der Ausgleichsgeraden. Auf der

linken Seite ist kein wahrer Effekt zu erkennen, auf der rechten Seite hingegen zwei wahre Effekte.

nur scheinbarer Natur sind, ordnen sich die Effektbeträge proportional zu den Quan-

tilschritten an. Hierzu werden die Effektbeträge in aufsteigender Reihenfolge sor-

tiert und mit den Quantilschritten zu Wertepaaren gruppiert. Die Ordinate des Half-

Normal-Plots hat die Einheit des Qualitätsmerkmals. Die Werte der Quantilschritte

sind in vielen Statistikbüchern tabelliert. Bei computergestützter Auswertung über-

nimmt das Auswerteprogramm die Erstellung ohnehin automatisch.

012

|E|

012

|E|

3.3 Beschreibungsmodell 67

0 0,4 0,8 1,2 1,6 2 2,4

Standardabweichungen

0,2

0,4

0,6

0,8

1,2

1,4

1,6

0 0,4 0,8 1,2 1,6 2 2,4

Standardabweichungen

0,2

0,4

0,6

0,8

1,2

1,4

1,6

1,8

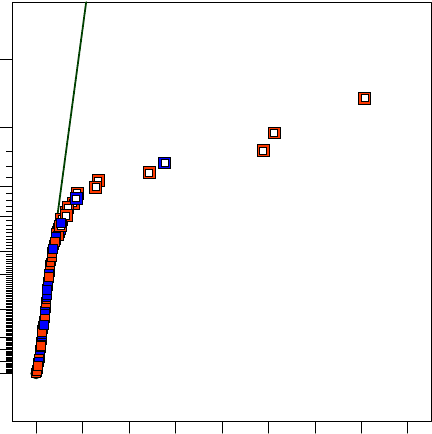
Abb. 3.6 Daniel-Plots für einen Versuchsplan mit fünf Faktoren und 16 Versuchsläufen. Unter-

sucht wurde das Qualitätsmerkmal Reichweite beim Rasensprenger (siehe Anhang), mit den Fak-

toren: Düsenwinkel α (A), β (B), Düsenquerschnitt (C), ﬂüssige Reibung (D) und Druck (E). Den

Ergebnissen wurde ein normalverteiltes Rauschen überlagert, um Teststreuung zu simulieren. Oben

ist der Rauschanteil niedrig (σ = 0, 02m), unten ist der Rauschanteil sehr hoch (σ = 0,5m, also in

der Größenordnung der starken Effekte). Auch bei starker Teststreuung dämpft der Versuchsplan

die Auswirkung der Störung wirkungsvoll. Die starken Effekte bleiben erkennbar.

Die scheinbaren Effekte ordnen sich entlang einer Geraden an, da Quantilschritte

und Effektbeträge in einem proportionalen Zusammenhang stehen. Wahre Effekte

liegen oberhalb der Geraden, weil sie stärker sind, als es die Zufallsstreuung er-

warten lässt. Wegen der Sortierung in aufsteigender Reihenfolge beﬁnden sich ty-

pischerweise die scheinbaren Effekte in der Nähe des Koordinatenursprungs und

die wahren Effekte in der rechten oberen Ecke. Insbesondere bei kleineren Ver-

68 3 Kontrollverfahren

        























Abb. 3.7 Daniel-Plot der Effekte. Der Half-Normal-Plot kann auch achsenvertauscht aufgetragen

sein. Viele Programme liefern dies als Voreinstellung. Die Effektbeträge (als unfreie Größe) wer-

den dann auf der Abszisse und die kumulierte Häuﬁgkeit auf der Ordinate dargestellt. Die Achsen-

transformation ist analog zur Transformation durch die Quantilschritte, nur die Skalen sind anders.

Daher kann man auch hier die wahren Effekte daran erkennen, dass sie nicht zur Ausgleichsgera-

den passen.

suchsplänen streuen die scheinbaren Effekte um die Gerade, weil die Mittelwerte

nur aus wenigen Messergebnissen gebildet werden. Als wahre Effekte gelten nicht

alle Punkte oberhalb der Geraden, sondern nur diejenigen, die grundsätzlich nicht

zum Verlauf der Geraden passen. In der Praxis wird man drei Gruppen vorﬁnden:

1. Effekte, die sich sicher den scheinbaren Effekten zuordnen lassen und um eine

Ausgleichsgerade gruppieren. 2. Starke Effekte, die deutlich über der Geraden lie-

gen und mit hoher Wahrscheinlichkeit als wahre Effekte reproduzierbar sind. 3. Die

“Grauzone” aus Effekten, die nicht eindeutig zuzuordnen sind.

Kleine Versuchspläne liefern weniger Punkte zur Konstruktion des Half-Normal-

Plots. Bei Versuchsplänen der Auﬂösung III und IV sind die Effekte vermengt, was

dazu führen kann, dass kein Effektbetrag klein ist. Dann liegt die Ausgleichsge-

rade etwas höhenversetzt und schneidet nicht mehr den Koordinatenursprung. In

den meissten Fällen reicht jedoch der Half-Normal-Plot völlig aus, um eine siche-

re Entscheidung zu treffen. Die Erstellung dieser Diagramme übernehmen alle gu-

ten Auswerteprogramme. Für den Anwender genügt es also, die Grundidee dieses

Diagramms zu verstehen und ein Gefühl für die Zuordnung der Effekte in die je-

weiligen Kategorien zu entwickeln. In der “Grauzone” löst der Half-Normal-Plot

im Vergleich zur Varianzanalyse besser auf und stellt deswegen in jedem Fall eine

sinnvolle Ergänzung dar.

3.3 Beschreibungsmodell 69

     



























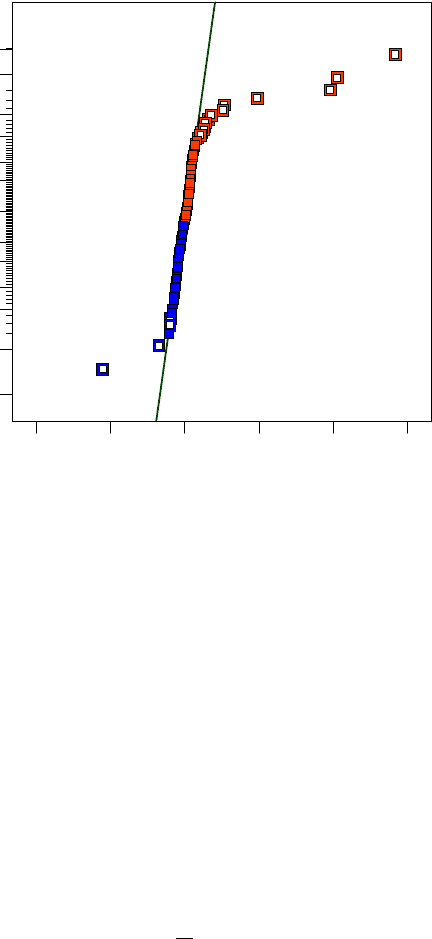
Abb. 3.8 Full-Normal-Plot der Effekte. Beim Full-Normal-Plot entfällt die Betragsbildung der

Effekte. Auch hier zeichnen sich wahre Effekte dadurch aus, dass sie nicht zur Ausgleichsgeraden

passen. Sie tauchen aber in zwei Regionen auf, je nach ihrem Vorzeichen.

3.3.2 Varianzanalyse

Die Varianzanalyse (ANalysis Of VAriance, ANOVA) bildet das rechnerische Ge-

genstück zum Half-Normal-Plot. Die Aufgabe ist gleich, die Grundidee des Hypo-

thesentests ebenfalls. Im Unterschied zur graphischen Lösung berechnet die ANO-

VA die Wahrscheinlichkeitswerte, um wahre Effekte von scheinbaren Effekten zu

unterscheiden. Die Varianzanalyse liefert darüber hinaus auch zusätzliche Informa-

tionen zur Güte des Beschreibungsmodells. Auch die Varianzanalyse gehört zum

normalen Leistungsumfang eines Auswerteprogramms, also genügt an dieser Stelle

die Erläuterung des Grundprinzips.

Ausgangspunkt für die ANOVA ist die in der Versuchsreihe aufgetretene Ge-

samtvarianz. Diese berechnet sich aus den Werten aller Versuche und dem Gesamt-

mittelwert.

ges

∑

i=1

− ¯y)

(3.7)

Im zweiten Schritt erfolgt die Berechnung der Teilvarianzen, die sich den ein-

zelnen Faktoren zuordnen lassen. Abbildung x zeigt, wie man sich diese Aufteilung

vorstellen kann. Der Effekt des jeweiligen Faktors bewirkt im Mittel eine Verschie-

bung aller Ergebnisse um den halben Effektbetrag. Die verbleibende Varianz steht

70 3 Kontrollverfahren

Faktor E

−1 +1

mittlere Verschiebung

durch den Eﬀekt des Faktors

Streuung, die nicht durch diesen Faktor verursacht wurde

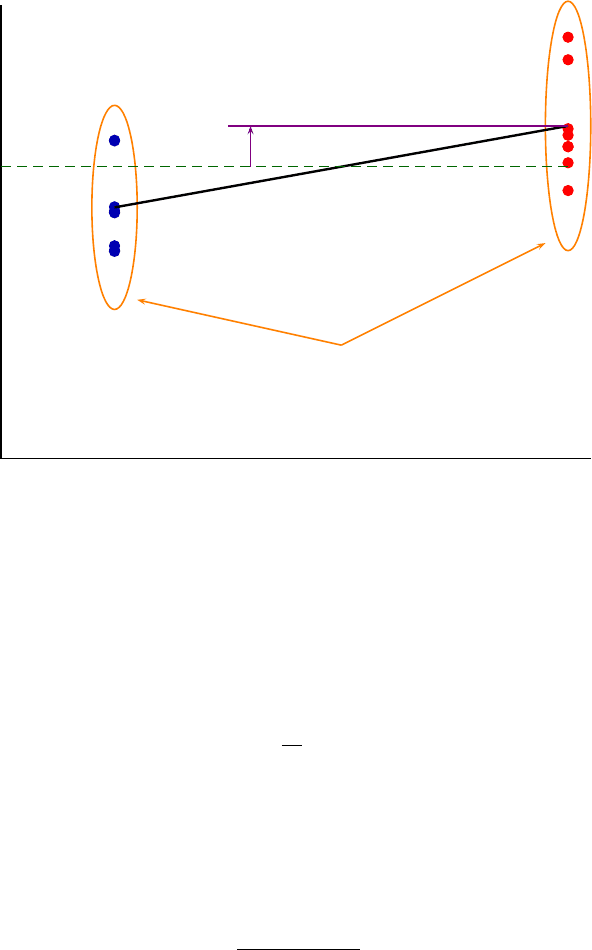
Abb. 3.9 Aufteilung der auftretenden Streuung. Der untersuchte Faktor (hier Faktor E, also Druck

aus dem Fallbeispiel Rasensprenger) verschiebt im Mittel jeden Datenpunkt um den halben Effekt-

betrag. Die übrige Streuung wird von anderen Faktoren verursacht oder fällt unter die allgemeine

Teststreuung.

nicht mit dem untersuchten Faktor in Verbindung, denn sie tritt bei konstanter Ein-

stellung dieses Faktors auf. Der Effekt des Faktors erzeugt somit eine Teilvarianz.





(3.8)

Unabhängige Teilvarianzen überlagern sich additiv, also entsteht die Gesamtvari-

anz aus ihrer Summe. Ein System mit n

Gleichungen und n

Modellkonstanten hat

−n

) Freiheitsgrade, denn jede Modellkonstante (auch der Gesamtmittelwert)

bindet einen Freiheitsgrad. V

bezeichnet den Erwartungswert der Teilvarianz pro

Freiheitsgrad.

ges

−

∑

−1

j=1

−n

(3.9)

Von der Gesamtvarianz werden also zunächst alle Teilvarianzen der Effekte ab-

gezogen. Der nicht durch die Effekte erklärbare Restbetrag verteilt sich auf die übri-

gen Freiheitsgrade. Im nächsten Arbeitsgang erfolgt ein Vergleich der Teilvarianzen

mit diesem Erwartungswert. Das liefert eine dimensionslose Kennzahl, das soge-

3.3 Beschreibungsmodell 71

nannte F-Verhältnis (F-ratio). Liegt die Teilvarianz deutlich über dem Erwartungs-

wert ist das F-Verhältnis deutlich größer als 1 und die Wahrscheinlichkeit ist groß,

dass es sich hierbei um einen wahren Effekt handelt. Bei großen Feldern stellt 4

die Signiﬁkanzgrenze dar, unter der Annahme einer fünfprozentigen Irrtumswahr-

scheinlichkeit. Bei kleinen Feldern oder voll besetzten Feldern

ist der berechnete

Erwartungswert weniger stabil, denn die Zahl der verbleibenden Freiheitsgrade ist

gering. Bei gleicher Irrtumswahrscheinlichkeit muss daher der Grenzwert für das

F-Verhältnis ansteigen. Die Statistik benutzt quasi einen Sicherheitszuschlag. Statt

der Varianz verwenden Auswerteprogramme meist die “Quadratsumme” oder (sum

of squares), weil n

, also die Zahl der Versuchsläufe, bei der Quotientenbildung (F-

Verhältnis) ohnehin entfällt. Im Kapitel Statistische Modellbildung wird die ANO-

VA im Detail erklärt.

Ursache Quadratsumme FG F-Quotient p-Wert

A 4,566110 1 491,12 0,0000

0,134044 1 14,42 0,0067

C 4,115280 1 442,63 0,0000

D 0,227843 1 24,51 0,0017

8,258640 1 888,28 0,0000

AC 0,853954 1 91,85 0,0000

0,048472 1 5,21 0,0564

CE 0,240382 1 25,85 0,0014

Rest 0,065081 7

Tabelle 3.7 ANOVA für das Fallbeispiel Rasensprenger mit 16 Versuchsläufen und fünf Fakto-

ren auf jeweils zwei Stufen. Die Teststreuung ist in diesem Fall so stark, dass kleinere Effekte

als Scheineffekte eingestuft werden und nicht den Grenzwert F

kr it

erreichen. Diese wurden in der

Tabelle bereits aussortiert. Zur Berechnung von F wird zunächst der nicht durch die Effekte erklär-

bare Anteil (Rest) durch die Zahl der verfügbaren Freiheitsgrade geteilt (hier: 16-9, also 7). Diese

“erwartete Quadratsumme pro Freiheitsgrad” gilt als Referenz (hier: 0,00930). F ist der Quotient

aus Quadratsumme und Referenzwert. Der p-Wert bezeichnet die statistische Irrtumswahrschein-

lichkeit für die Entscheidung, den Effekt als wahr einzustufen.

Auswerteprogramme berechnen aus dem F-Verhältnis unter Berücksichtigung

der verfügbaren Freiheitsgrade automatisch die Irrtumswahrscheinlichkeit für die

Annahme, dass der jeweilige Effekt wahr ist. Für diesen p-Wert gilt 0,05 üblicher-

weise als Grenze, entsprechend einer fünfprozentigen Irrtumswahrscheinlichkeit.

Unter 0,05 gilt der Effekt als wahr, über 0,05 als scheinbarer Effekt. Natürlich steckt

in der Festlegung des Grenzwertes eine gewisse Willkür und bei kleinen Feldern

besteht die Gefahr, dass wahre Effekte ausgemustert werden. Der Hypothesentest

sichert leider nur eine Richtung, schützt also davor, einen scheinbaren Effekt als

wahren Effekt anzusehen. Unklar bleibt folglich, mit welcher Wahrscheinlichkeit

ein wahrer Effekt irrtümlicherweise als scheinbarer Effekt eingestuft wird und dem

Beschreibungsmodell verloren geht.

Voll besetzte Felder nennt man auch: “gesättigt”.

72 3 Kontrollverfahren

0 5 10 15 20 25 30

− n

krit

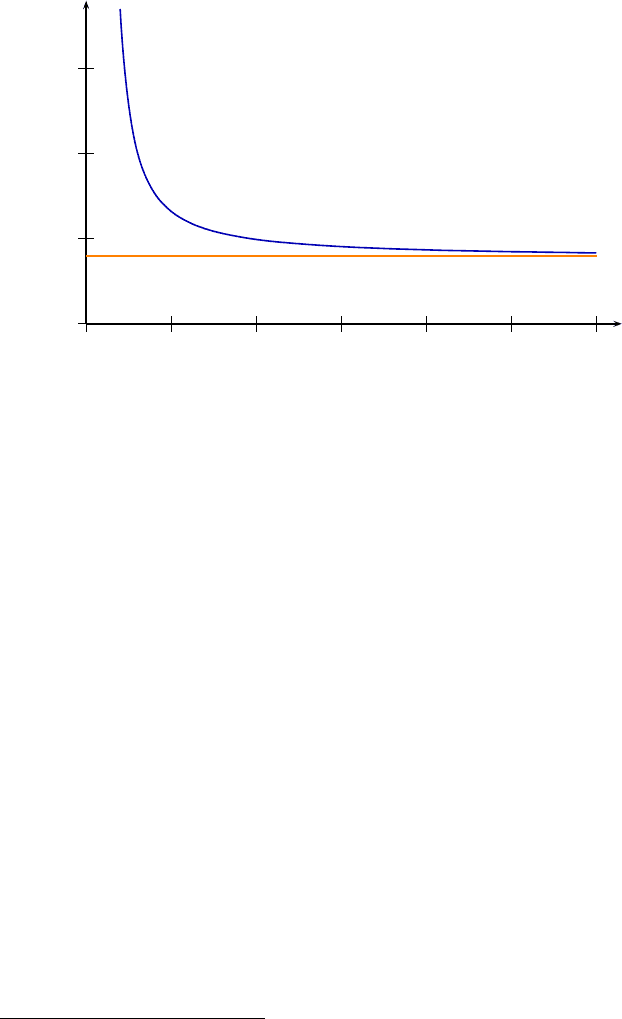
Abb. 3.10 Grenzkurve für F. Bei einer hohen Zahl von verfügbaren Freiheitsgraden konvergiert

der Grenzwert gegen 4. Wenn nur wenige Freiheitsgrade zur Verfügung stehen, muss F einen

wesentlich höheren Wert erreichen, um mit gleicher statistischer Sicherheit die wahren von den

scheinbaren Effekten zu trennen.

Versuchswiederholungen liefern ebenfalls Freiheitsgrade. Bei Anwendung der

Varianzanalyse ist es immer ratsam, keine Mittelwertbildung außerhalb des Aus-

werteprogramms durchzuführen, sondern die Versuche tatsächlich einzeln zu be-

trachten. Hierzu kopiert man den Versuchsplan entsprechend der Zahl der Wieder-

holungen untereinander

und trägt die einzelnen Versuchsergebnisse ein. Beispiel:

Ein Versuchsplan mit 8 Kombinationen und 2 Wiederholungen liefert insgesamt 24

Versuchsergebnisse. Ist er mit 7 Faktoren besetzt, verbleiben 16 Freiheitsgrade für

die Varianzanalyse.

Auf diese Weise bietet die ANOVA im Gegensatz zum Half-Normal-Plot auch

die Möglichkeit, die Varianz der Versuchswiederholungen zu analysieren. Der Ver-

gleich der Gesamtvarianz mit der Summe der durch die Effekte erzeugten Teilva-

rianzen gibt Aufschluss über die Güte des Beschreibungsmodells, allerdings nur in

Bezug auf die getesteten Kombinationen. Ist die Differenz klein, erklären die Effek-

te die Systemantwort fast vollständig. Hierbei ist jedoch Vorsicht geboten. Bleiben

scheinbare Effekte im Beschreibungsmodell, so wird dieses fälschlicherweise zu

genau an die jeweiligen Testdaten angepasst (over-ﬁt). Die Varianzanalyse gaukelt

dann eine hohe Modellgüte vor, weil die Restvarianz klein ist. Eine Versuchswieder-

holung oder Tests mit neuen Kombinationen führen in diesem Fall zu enttäuschen-

den Ergebnissen. Ohne die scheinbaren Effekte steigt zwar die Restvarianz, aber

Viele Auswerteprogramme bieten diese Option automatisch an. In anderen Fällen kann man

dies leicht durch ein benutzerdeﬁniertes Feld bewerkstelligen.

3.4 Genauigkeit der Vorhersage 73

das Beschreibungsmodell ist trotzdem besser, weil es nicht “hinter den verrauschten

Testdaten herläuft”.

Im Verbund geben die Varianzanalyse und der Half-Normal-Plot ein hohes Maß

an Sicherheit bei der Beurteilung des gewählten Beschreibungsmodells. Die sta-

tistische Analyse ersetzt jedoch kein Fachwissen. Aus diesem Grund ist es immer

ratsam, nach einer physikalischen Erklärung für die Effekte zu suchen. Oft bringt

dieser Dialog zwischen dem Statistiker und dem Anwender aus der entsprechenden

Fachabteilung das eigentliche Systemverständnis.

3.4 Genauigkeit der Vorhersage

Eine wesentliche Aufgabe der Methode besteht in der Vorhersage neuer Einstellun-

gen innerhalb des Faktorraums. Natürlich muss dies mit hinreichender Genauigkeit

geschehen, sonst sind die Vorhersagen unbrauchbar und führen im schlimmsten Fall

zu falschen Schlussfolgerungen. Wie bei allen Modellen, muss man grundsätzlich

mit Abweichungen zwischen Vorhersage und Realität rechnen. Es stellen sich nun

Fragen nach dem Ausmaß und den Ursachen der Abweichungen. In der Praxis wird

man immer eine Kombination mehrerer Ursachen vorﬁnden und es gilt diese vonein-

ander abzugrenzen, damit im Bedarfsfall Deﬁzite gezielt beseitigt werden können.

Auch hier liefert die klassische Regressionsanalyse ein ganzes Arsenal an Kontroll-

verfahren, um sicher zum Ziel zu gelangen.

Nach Anwendung der Kontrollverfahren muss die Ursachenanalyse natürlich auf

die gesamte Versuchsdurchführung ausgedehnt werden. Oft gibt es simple Über-

tragungsfehler oder Fehler bei der Umrechnung der Rohdaten in die untersuchten

Qualitätsmerkmale. In vielen Fällen führen gerade die unerwarteten Ergebnisse zu

wertvollen Erkenntnissen, sei es indem sie auf unberücksichtigte Faktoren hinwei-

sen oder auf physikalische Effekte, mit denen nicht gerechnet wurde. Dieser Teil

der Analyse hat nicht mehr mit Statistik zu tun, es geht vielmehr um eine fachlich

fundierte Interpretation der Ergebnisse.

3.4.1 Fallbeispiel

Rasensprenger, siehe Abbildung 3.11 und Anhang. Untersucht wurde das Quali-

tätsmerkmal Reichweite mit den Faktoren: Düsenwinkel α (A), β (B), Düsenquer-

schnitt (C), Durchmesser (D), trockene Reibung (E), ﬂüssige Reibung (F) und Druck

(G), entsprechend den Einstellungen aus Tabelle 2.9. Als Versuchsplan kam ein

Vollfaktorplan mit 128 Versuchen zum Einsatz. Überlagertes normalverteiltes Rau-

schen mit σ = 0,1m dient als Ersatz für die Teststreuung. Einen absichtlich einge-

bauten Ausreißer in Versuchslauf 13 gilt es zu entdecken.

74 3 Kontrollverfahren

zul

, M

α vertikaler D

usenwinkel

β tangentialer D

usenwinkel

usenquerschnitt

d Durchmesser, Spr

uhkopf

zul

Zuleitungsdurchmesser

Reibungsmoment, ﬂ

ussig

Reibungsmoment, trocken

Eingangsdruck

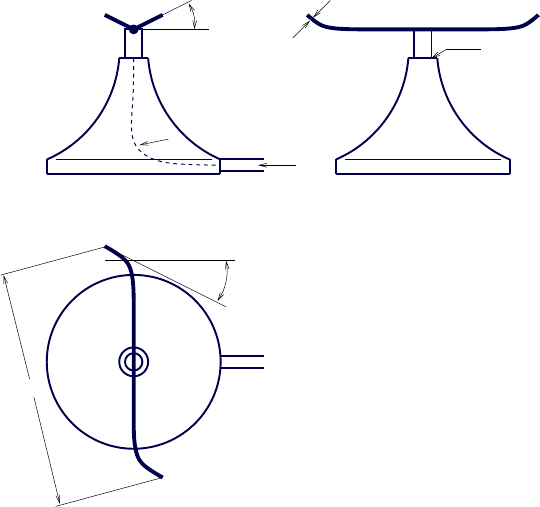
Abb. 3.11 Schematische Darstellung eines Rasensprengers.

3.4.2 Residual-Plots

Nutzt man das Beschreibungsmodell, um Vorhersagewerte für die bereits getesteten

Kombinationen zu berechnen, eröffnet sich ohne zusätzlichen Versuchsaufwand ei-

ne weitere Kontrollmöglichkeit. Der Residualplot zeigt die Abweichung zwischen

Vorhersage und Testergebnis. Große Abweichungen können verschiedene Ursachen

haben, zum Beispiel einzelne Ausreißer, ein zu grobes Beschreibungsmodell, eine

hohe Teststreuung oder einen dejustierten Versuchsaufbau. Unterschiedliche Dar-

stellungsweisen erleichtern die Ursachenanalyse.

Die Darstellung predicted vs. actual zeigt die Vorhersage im Vergleich zu den

gemessenen Werten. Diese Darstellung eignet sich hervorragend für einen schnel-

len Überblick, weil sie die Abweichungen sofort in Relation zu den auftretenden

Werten setzt. Dies vereinfacht die Entscheidung darüber, ob die erreichte Modell-

güte bereits den Erwartungen entspricht oder weitere Analysen notwendig werden.

Streng genommen ist dies noch kein Residual-Plot, ﬁndet sich aber bei Auswerte-

programmen typischerweise in dieser Kategorie.

Die Darstellung residual vs. run order zeigt die Residuen in der Reihenfolge

der Versuche und ist eines der wichtigsten Diagnosewerkzeuge, weil es unmittel-

bar aufzeigt, in welchen Versuchen die Abweichungen zwischen Vorhersage und

Testergebnis besonders gross sind. Viele potentielle Fehler lassen sich hier able-