Шпаргалки по логике
Подождите немного. Документ загружается.

А Е
I О
б) Подчинение – это отношение между такими суждениями, у которых количество различно, а качество одинаково: A
– I, E – O.Закономерности отношения подчинения таковы:
- из истинности подчиняющего А или Е, следует, соответственно, истинность подчиненного I или О, но не наоборот.
- из ложности подчиненного I или О следует, соответственно, ложность подчиняющего А или Е, но не наоборот.
(Если истинно А, «Все адвокаты – юристы, то тем более истинно I»: «Некоторые адвокаты – юристы»). Но если
истинно I: «Некоторые свидетели дают верные показания», то отсюда еще не следует, что истинно А: «Все свидетели
дают верные показания». В данном случае это ложное суждение. Для других примеров в некоторых случаях А может
быть и истинным.
в) Частичная совместимость: одинаковое количество, разное качество I - О. Закономерность такова:
- оба суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Истинно I:
“Некоторые свидетели правдивы», может оказаться истинным и О: «Некоторые свидетели не являются
правдивыми». Имеет место и второй вариант. Истинно I: «Некоторые адвокаты – юристы», но это не значит, что
истинно О: «Некоторые адвокаты – не являются юристами», в данном случае О является ложным.
Несовместимые суждения. Они бывают двух видов.
а) Противоположность: А и Е, одинаковое количество, разное качество. Закономерность такова:
- оба суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Т.е.
закономерность обратная отношению частичной совместимости. (Если истинно А: «Все адвокаты – юристы», то с
необходимостью ложно Е: «Ни один адвокат не юрист», но если ложно А: «Все философы материалисты», то отсюда
еще не следует с необходимостью истинность Е: «Ни один философ не материалист». В данном случае последнее
суждение ложно.
б) Противоречие (контрадикторность) – А - О, Е - I.
-Противоречащие суждения не могут быть одновременно истинными и одновременно ложными. Если истинно А:
«Все адвокаты – юристы», то ложно О, что «Некоторые адвокаты – не юристы». Если ложно А: «Все свидетели
правдивы», то истинно О: «Некоторые свидетели не правдивы».
таблица истинности (и) и ложности (л), а также неопределенности (н) простых, категорических суждений А, Е, I, О.
А Е I О
А
И
Л
– Л
Н
И
Н
Л
И
Е
И
Л
Л
Н
– Л
И
И
Н
I
И
Л
Н
Л
Л
И
– Н
И
О
И
Л
Л
И
Н
Л
Н
И
–
20. Сложное суждение и его виды.
Сложные суждения образуются из простых путем разного рода их соединения. Обычно характеристики простых и
сложных суждений не вызывают затруднений. Однако возможны ситуации, когда граница между простым и
сложным суждениями должна быть признана до определенной степени условной. Это относится к таким
конструкциям, в которых не без оснований можно выявить как одно утверждение (или отрицание), так и два, три.
Оценка подробного суждения как простого или сложного в известной степени зависит от позиции исследователя.
Возьмем суждение: «Этот человек сотрудник ОВД и спортсмен». Его можно рассматривать и как простое, если
исходить из того, что словосочетание «сотрудник ОВД и спортсмен» выражает одно понятие. С другой стороны мы
можем предположить, что человек, о котором идет речь является сотрудником, но спортом никогда не занимался.
Выходит, что рассматриваемая нами конструкция наряду с истинной информацией содержит и ложную. Эта ложная
информация не может заключаться в понятии «спортсмен», ибо понятие не обладает значением истинности.
Носители истинностного значения выступает суждение. Но может ли одно суждение быть носителем двух значений
истинности? Это возможно лишь в том случае, когда суждение состоит из двух суждений, т.е. является сложным.
V
V
Таким образом, есть основание трактовать данное суждение как сложное, состоящее из двух утверждений: «Этот
человек сотрудник ОВД» и «Этот человек спортсмен».
Виды сложных суждений по характеру логического союза.
1. Конъюнктивные (или соединительные) суждения. Они образуются из исходных простых суждений посредством
логического союза конъюнкции «и» (символически «») А В, т.е. А и В. В русском языке логический союз
конъюнкции выражается многими грамматическими союзами: и, а, но, да, хотя, а также, не смотря на то, что. «Я
буду поступать в институт, несмотря на то, что придется сильно потрудиться». Иногда не требуется никаких союзов.
Вот высказывание одного из Американских президентов начала 20 века: «Перед нами новая эра, в которой мы,
очевидно, будем управлять миром».
Возможно 4 способа сочетания двух исходных суждений «А» и «В» в зависимости от их истинности и ложности.
Конъюнкция истинна в одном случае, если истинно каждое из суждений.Вот таблица конъюнкции.
А В А В
И
И
Л
Л
И
Л
И
Л
И
Л
Л
Л
2. Дизъюнктивные (разделительные) суждения.
а) слабая (нестрогая) дизъюнкция образована логическим союзом «или». Она характеризуется тем, что
объединяемые суждения не исключают друг друга. Формула: А V В (А или В). Союзы «или», «либо» используются
здесь в разделительно-соединительном значении. Пример: «Понцов является юристом или спортсменом». (Он может
оказаться и юристом и спортсменом одновременно).Слабая дизъюнкция истинна когда хотя бы одно из суждений
истинно.
А В А V В
И
И
Л
Л
И
Л
И
Л
И
И
И
Л
Смысловая граница между конъюнкцией и слабой дизъюнкцией в известном отношении условна.
б) сильная (строгая) – логический союз «либо … либо», . Ее составляющие (альтернативы) исключают друг друга:
А В. (либо А либо В). Она выражается по существу теми же грамматическими средствами, что и слабая: «или»,
«либо», но уже в ином разделительно - исключающем значении. «Мы выживем или погибнем». «Амнистия бывает
общей или частичной». Строгая дизъюнкция истинна, когда одно из суждений истинно, а другое ложно.
А В А V В
И
Л
И
Л
Л
И
И
Л
И
И
Л
Л
3. Импликативные (условные суждения). В них объединяют суждения на основе логического союза «если …, то», и
«тогда…, когда» (символ «→»), (А → В; если А, то В). «Если погода наладится, то мы найдём следы преступника».
Суждение, стоящее после слов «если», «тогда» называют антецедентом (предшествующее) или основанием, а
стоящее после «то», «когда» - консеквентом (последующее) или следствием. Импликация истинна всегда, кроме
случая, когда основание истинно, а следствие ложно.Необходимо помнить, что союз «если…, то» может
употребляться и в сопоставительном смысле («Если сам порох изобрели в Китае в древности, то оружие на основе
использования свойств пороха появилось в Европе только в средневековье») и, как легко убедиться, может выражать
вовсе не импликацию, а конъюнкцию.
А В А→ В
И
И
Л
Л
И
Л
И
Л
И
Л
И
И
4. Эквивалентные (равнозначные) суждения. В них объединяются суждения с взаимной (прямой и обратной)
зависимостью. Ее образует логический союз «если и только если …, то», «тогда и только тогда…, когда», «только
при условии», «лишь в случае» символ «↔» (А ↔ В), если и только если А, то В). «Если и только если у гражданина
большие заслуги перед РФ, он имеет право на получение высокой награды ордена «Герой России». Используется
также знаки « = », « ≡ ». Эквиваленция истинна, когда оба суждения истинны, или оба ложны.
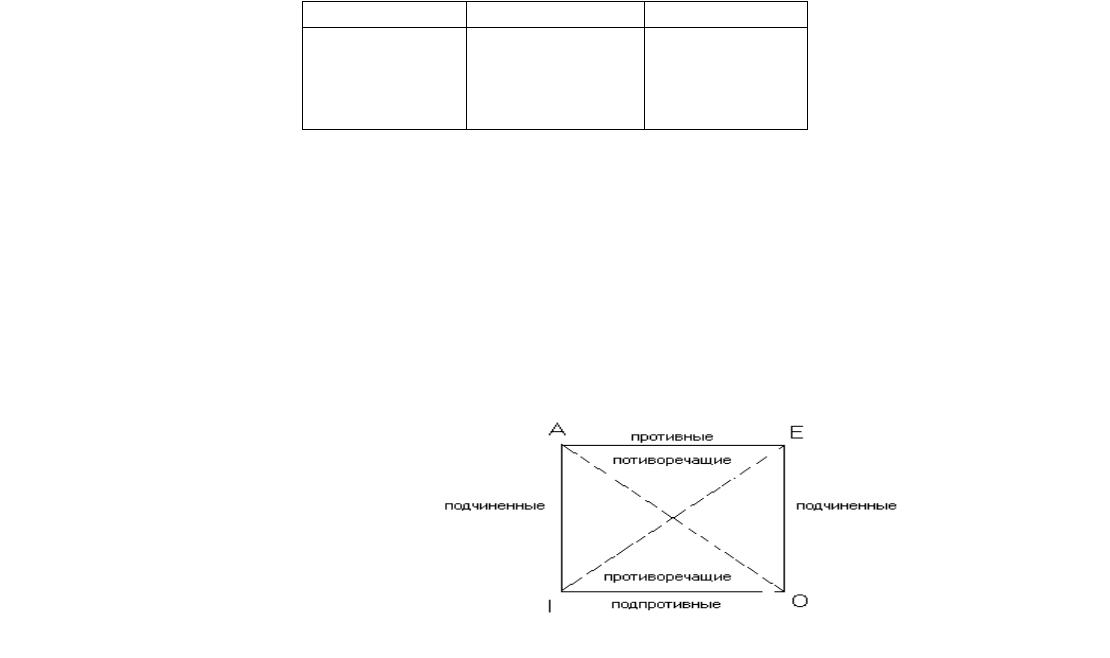
А В А ↔ В
И
И
Л
Л
И
Л
И
Л
И
Л
Л
И
Эквиваленция может быть истолкована и как конъюнкция двух импликаций, прямой и обратной: (р→q) (q → р).
Эквиваленцию иногда и называют двойной импликацией.
Подытоживая сказанное о сложных суждениях, надо отметить, что некоторые выделяют и, так называемое
контрфактическое суждение (союз «если…, то», символ « ● →». Это знак контрфактической импликации. Смысл
такой: ситуация, описываемая антицидентом, не имеет места, но если бы она существовала, то существовало бы
положение вещей, описываемое консеквентом. Например: «Если бы Понцов был мэром Красноярска, то не жил бы в
гостинке».
21. Условия истинности сложных суждений (табличное определение).
Суждения, в которых одно и то же подлежащее и сказуемое, но которые имеют разные качества или количества или
и то и другое, будут противоположными друг другу. Например, суждения А и I, суждения Е и А противоположны
друг другу.
Вопрос о
противоположности суждений имеет важное значение. Если я, возражая кому-нибудь, не признаю истинности его
утверждения, то я всё-таки нечто могу признавать истинным. Например, кто-нибудь утверждает, что все люди
мудры, и я это отрицаю, то я в то же время сознаю, что я могу признать истинность суждения «некоторые люди
мудры». Эти два суждения совместимы друг с другом. Если я утверждаю, что люди смертны, то я не могу в то же
время признавать, что некоторые люди не смертны. Одно суждение оказывается несовместимым с другим
суждением. Отсюда возникает необходимость рассмотреть все суждения с точки зрения их противоположности,
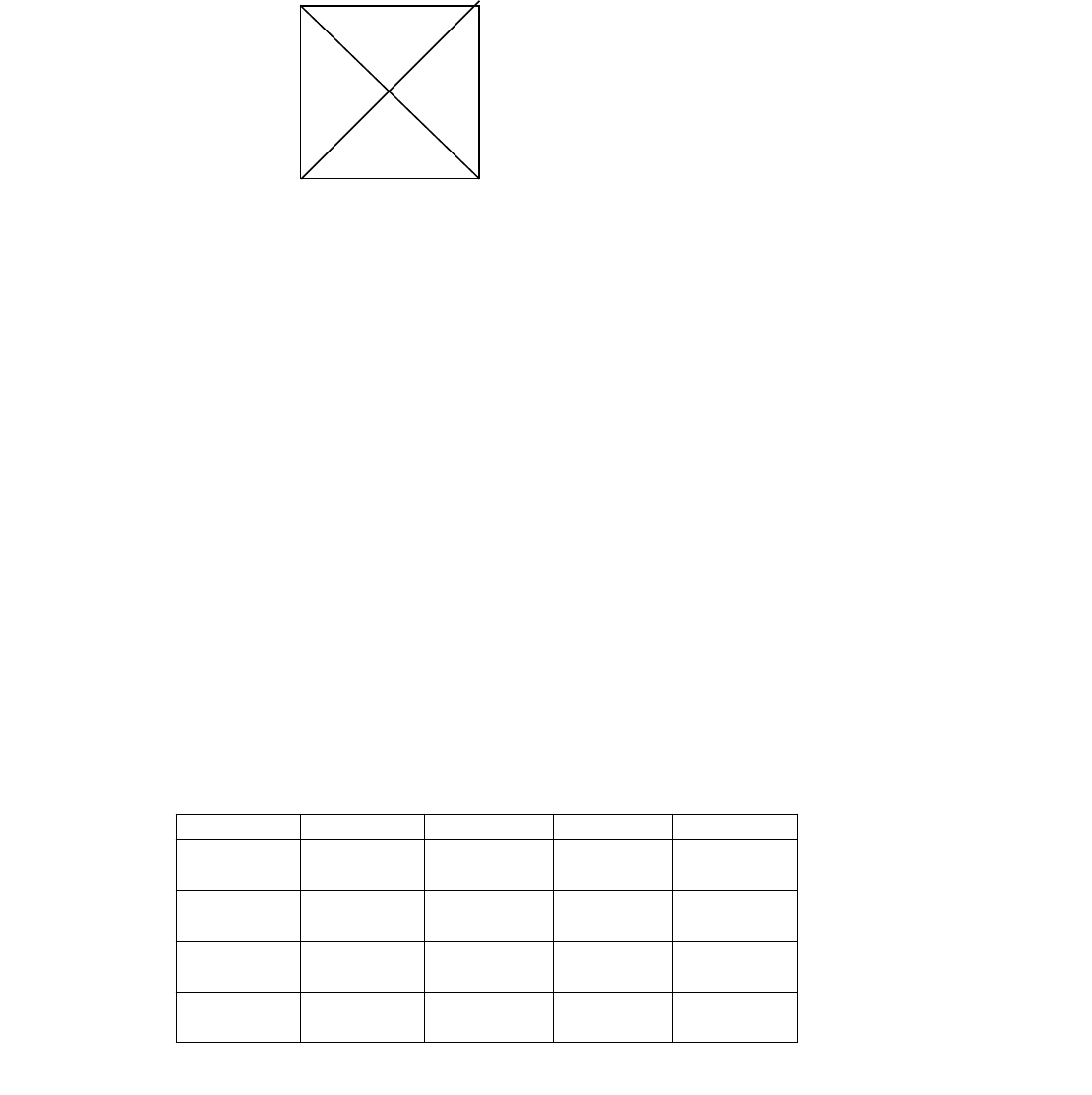
чтобы показать, какие суждения совместимы или не совместимы друг с другом.Для выяснения этого вопроса мы
воспользуемся схемой, известной под именем «логического квадрата». Схема эта наглядно показывает взаимное
отношение суждений всех четырёх классов.Возьмём квадрат и проведём в нём диагонали. У вершин четырёх его
углов поставим буквы А, Е, I, О, т. е. символы четырёх классов суждений. Возьмём какое-нибудь суждение и
представим его в формах суждений всех четырёх классов: А — «все люди честны», Е — «ни один человек не
честен», I — «некоторые люди честны», О — «некоторые люди не суть честны».Между суждениями А и О, Е и 1
существует отношение, которое называется противоречием» Эти суждения отличаются и во количеству и по
качеству.Отношение между А и Е называется противностью. Эти общие суждения отличаются друг от друга по
качеству.Между А и I, Е и О есть отношения подчинения. Здесь суждения отличаются по количеству.Между I и О
— отношение подпротивности. Здесь два частных суждения отличаются по качеству.Рассмотрим каждую пару этих
суждений в отдельности.
Противоречие (А — О, Е — I). Я высказываю суждение А — «все люди искренни». Вы находите, что это суждение
ложно. В таком случае вы должны признать истинным суждение О— «некоторые люди не искренни». Если вы не
допустите истинности этого последнего суждения, то вы не можете признать ложности суждения А. Следовательно,
при ложности суждения А, .суждение О должно быть истинным.Возьмём суждение О — «некоторые люди не суть
смертны». Это суждение мы должны признать ложным, потому что мы признаём- истинным суждение А — «все
люди смертны». Следовательно, при ложности О суждение А — истинно.Если я утверждаю, что все люди смертны, и
вы со мной соглашаетесь, т. е. находите, что это суждение истинно, то вы должны будете признать, что при
допущении истинности этого суждения нельзя признать истинности суждения О — «некоторые люди не смертны»,
и, наоборот, если признать истинность суждения О — «некоторые люди не суть честны», то никак нельзя будет
признать истинности суждения А — «все люди честны».Таким образом, из двух противоречащих суждений при
истинности одного суждения другое оказывается ложным, при ложности одного суждения другое является
истинным. Из этого следует, что из противоречащих суждений одно должно быть истинным, а другое —
ложным. Два противоречащих суждения не могут быть в одно и то же время оба истинными, но не могут быть
и оба ложными.
Противность (А — Е). Если признать суждение А — «все металлы суть элементы» истинным, то никак нельзя
допустить, что «ни один металл не есть элемент». Следовательно, если А истинно, то Е ложно. Если мы признаём
суждение Е — «ни один человек не всеведущ» истинным, то мы, конечно, не будем иметь никакого права
утверждать суждение А — «все люди всеведущи». Следовательно, если Е истинно, то А ложно. Таким образом, из
истинности одного из противных суждений следует ложность другого. Возьмём суждение А — «все бедняки
порочны» — и признаем, что это суждение ложно. Можно ли в таком случае утверждать суждение Е — «ни один
бедняк не порочен»? Конечно, нельзя, потому что в действительности может оказаться, что только некоторые
бедняки не порочны, а некоторые — порочны. Если я выскажу суждение Е — «ни один алмаз не драгоценен» — и вы
станете отрицать истинность этого :утверждения, то сочтёте ли вы себя вправе утверждать, что «все алмазы
драгоценны»? Конечно, нет. Отрицая моё утверждение, зы в свою очередь можете только утверждать, что
«некоторые алмазы драгоценны», допуская в то же время, что «некоторые алмазы не драгоценны». Следовательно,
при ложности одного из противных суждений нельзя признать истинность другого, потому что между ними всегда
может быть нечто среднее.Итак, в двух противных суждениях из истинности одного следует ложность другого, но из
сложности одного не следует истинность другого; оба суждения не могут быть истинными (потому что если одно
истинно, то другое ложно), но оба могут быть ложными (потому что при ложности одного ложным может быть
другое).
Подчинение (А—I, Е—О). Если А истинно, то I тоже, истинно. Например, если суждение А — «все алмазы
драгоценны» — истинно, то истинно суждение I — «некоторые алмазы драгоценны». Если Е истинно, то О тоже
истинно. Если «ни один человек не всеведущ», то, конечно, это предполагает, что «некоторые люди не всеведущи».
От истинности общих суждений, следовательно, зависит истинность частных.Если I истинно, то А может не быть
истинно. Например, суждение I — «некоторые люди мудры» — истинно. Будет ли следствие этого истинным
суждение А — «все люди мудры»? нет. Если О истинно, то Е может быть не истинно. Если мы признаём истинным
О — «некоторые люди не искренни», то можем и мы вследствие этого признать истинным суждение Е — «ни один
человек не искренен»? Конечно, нет.Ложность общего суждения оставляет неопределённой важность и истинность
подчинённого частного. При отрицании истинности А мы не можем сказать, будет ли I истинным или ложным. При
отрицании истинности Е мы не можем ни утверждать, ни отрицать истинности О. Если мы, например, отрицаем
истинность А — «все люди честны», то мы можем признавать тинным суждение I — «некоторые люди честны».
Если мы отрицаем суждение истинности Е — «ни один человек не есть мудр», то мы можем признавать истинность
О — «некоторые люди не суть мудры». Но ложность частного приводит к ложности общего. Если ложно, то А
ложно. Если нельзя сказать «некоторые люди всеведущи», потому что это ложно, то тем более нельзя сказать все
люди всеведущи». Если О ложно, то Е ложно. Если нельзя сказать «некоторые люди не суть смертны», то нельзя
сказать и один человек не есть смертей», потому что если чего-нибудь нельзя утверждать относительно части класса,
то этого же тем более нельзя утверждать относительно всего класса.Таким образом, истинность частного
суждения находится в зависимости от истинности общего суждения, но не наоборот; ложность частного
приводит к ложности общего, но не наоборот.
Подпротивная противоположность (I—О). Если I истинно, то О может быть истинно. Если истинно суждение
«некоторые люди мудры», то что сказать о суждении «некоторые (другие) люди не суть мудры»? Это суждение
может быть истинным, потому что одни люди могут быть мудрыми, а другие — немудрыми. Если О истинно, то I
может быть истинно. Если мы скажем, что «некоторые люди не суть искренни», то мы в то же время можем
предполагать, что «некоторые люди суть искренни»; одно суждение не исключает другого. Таким образом,
суждения I и О могут быть в одно и то же время истинными.Если I ложно, то О истинно. Если нельзя сказать
«некоторые люди всеведущи», то это происходит оттого, что истинно противоречащее суждение Е — «ни один
человек не есть всеведущ», а если это суждение истинно, то истинно подчинённое суждение О — «некоторые люди
не суть всеведущи».Если О ложно, то I истинно. Если ложно, что «некоторые люди не суть смертны», то это
происходит от истинности противоречащего суждения «все люди смертны», а из истинности этого суждения следует
истинность подчинённого суждения «некоторые люди смертны».Следовательно, оба подпротивных суждения
могут быть в одно. и то же время истинными, но оба не могут быть ложными (потому что при ложности одного
суждения другое является истинным).
Наибольшая противоположность. Мы рассмотрели пары суждений противных и противоречащих. наибольшую
противоположностьпредставляют суждения А и Е; между этими суждениями возникает наибольшая
противоположность, когда мы их сопоставляем друг с другом. Если кто-нибудь скажет, что «все книги содержат
правду», и мы на это замечаем, что «ни одна книга не содержит правды», то противоположность между первым
суждением и вторым чрезвычайно велика. Не так велика будет противоположность в том случае, если на
утверждение «все книги содержат правду» мы скажем, что «некоторые книги не содержат правды». Из этих
примеров видно, что противоположность между А и Е больше, чем между А и О, т. е. несогласие больше в первом
случае, чем во втором. Таким образом, наибольшая противоположность содержится в суждениях противных. Эта
противоположность называется диаметральной.Но хотя наибольшая противоположность существует между

суждениями противными, однако при опровержении суждений общеутвердительных и общеотрицательных гораздо
удобней пользоваться суждениями противоречащими, а не противными, потому что гораздо меньше риска в
утверждении I или О, чем в утверждении А или Е. Предположим, кто-нибудь утверждает — «все книги полезны».
Это утверждение можно отвергнуть, показав, что «ни одна книга не полезна», но можно отвергнуть, показав, что
«некоторые книги не полезны». Этот второй способ опровержения предпочтительнее по следующей причине. В
самом деле, если мы покажем, что «некоторые книги не полезны», то этого вполне достаточно для того, чтобы
отвергнуть положение «все книги полезны». Гораздо легче показать бесполезность только некоторых книг, чем
показать, что ни одна книга не полезна. Гораздо меньше риска утверждать О, чем , утверждать Е. По этой причине
мы редко опровергаем общеутвердительное суждение при помощи общеотрицательного, но гораздо чаще при
помощи противоречащего частноотрицательного. То же самое справедливо относительно другой пары
противоречащих суждений.Всё сказанное выше об отношении суждений можно изобразить при помощи следующей
таблицы:
Если A
истинно,
То E ложно, O ложно, I истинно
E A ложно I ложно O истинно
I A
неопределенно
O
неопределенно
E ложно
O E
неопределенно
I
неопределенно
A ложно
Если A
ложно,
E
неопределенно
I
неопределенно
O истинно
E A
неопределенно
I истинно O
неопределенно
I A ложно E истинно O истинно
O A истинно E ложно I истинно
22. Модальные суждения.
Простые суждения бывают модальными (modus – образ, способ). Дело в том, что кроме основного содержания
всякое суждение несет с собой дополнительную смысловую нагрузку. Модальность суждений выражается словами:
«возможно», «ценно», «ничтожно» и им подобных, а также их отрицаний «невозможно», «не разрешено» и др.
Наиболее важными выступают такие виды модальности.
Истинная или алетическая модальность выражает характер связи между мыслимыми предметами. Модальными
словами служат слова «возможно», «необходимо», «случайно», и их синонимы.
Нормативная или деонтическая модальность относится к нормам людей, образам поведения в обществе. Слова
«разрешается», «запрещается», «обязательно» и их аналоги.
Познавательная или эпистемическая модальность означает характер и степень достоверности знания. Слова
«проблематично», «доказано», «опровергнуто» и им подобных.
Ценностная или аксиологическая модальность выражает отношение человека к материальным и духовным
ценностям. Слова «хорошо», «плохо», «безразлично». Каждый вид модальности имеет свою символическую запись.
23. Закон тождества.
Любая мысль в процессе рассуждения должна иметь определенное, устойчивое содержание. Это коренное свойство
мышления — его определенность — выражает закон тождества: всякая мысль в процессе рассуждения должна
быть тождественна самой себе (а есть а, или а=а, где под а понимается любая мысль).
Закон тождества может быть выражен формулой р—>р (если р, то р), где р — любое высказывание, —> — знак
импликации.
Из закона тождества следует: нельзя отождествлять различные мысли, нельзя тождественные мысли принимать за
нетождественные. Нарушение этого требования в процессе рассуждения нередко бывает связано с различным
выражением одной и той же мысли в языке.Например, два суждения: «Н. совершил кражу» и «Н. тайно похитил
чужое имущество» — выражают одну и ту же мысль (если, разумеется, речь идет об одном и том же лице).
Предикаты этих суждений — равнозначные понятия: кража и есть тайное хищение чужого имущества. Поэтому
было бы ошибочным рассматривать эти мысли как нетождественные.С другой стороны, употребление многозначных
слов может привести к ошибочному отождествлению различных мыслей. Например, в уголовном праве словом
«штраф» обозначают меру наказания, предусмотренную Уголовным кодексом, в гражданском праве этим словом
обозначают меру административного воздействия. Очевидно, употреблять подобное слово в одном значении не
следует.Отождествление различных мыслей нередко связано с различиями в профессии, образовании и т.д. Так
бывает в следственной практике, когда обвиняемый или свидетель, не зная точного смысла некоторых понятий,
понимает их иначе, чем следователь. Это нередко приводит к путанице, неясности, затрудняет выяснение существа

дела. Отождествление различных понятий представляет собой логическую ошибку — подмену понятия, которая
может быть как неосознанной, так и преднамеренной. Соблюдение требований закона тождества имеет важное
значение в работе юриста, требующей употребления понятий в их точном значении. При разбирательстве любого
дела важно выяснить точный смысл понятий, которыми пользуются обвиняемый или свидетели, и употреблять эти
понятия в строго определенном смысле. В противном случае предмет мысли будет упущен и вместо выяснения дела
произойдет его запутывание.
24. Закон непротиворечия.
Логическое мышление характеризуется непротиворечивостью. Противоречия разрушают мысль, затрудняют процесс
познания. Требование непротиворечивости мышления выражает формально-логический закон непротиворечия: два
несовместимых друг с другом суждения не могут быть одновременно истинными; по крайней мере одно из
них необходимо ложно
1
.
Этот закон формулируется следующим образом: неверно, что а и не-а (не могут быть истинными две мысли, одна из
которых отрицает другую). Он выражается формулой (р л~\р) (неверно, что р и не-р одновременно истинны). Под р
понимается любое высказывание, под ~1 р — отрицание высказывания р, знак I перед всей формулой — отрицание
двух высказываний, соединенных знаком конъюнкции. Закон непротиворечия действует в отношении всех
несовместимых суждений
2
. Для правильного его понимания необходимо иметь в виду следующее. Утверждая что-
либо о каком-либо предмете, нельзя, не противореча себе, отрицать (1) то же самое (2) о том же самом предмете, (3)
взятом в то же самое время и (4) в том же самом отношении.
Понятно, что не будет противоречия между суждениями, если в одном из них утверждается принадлежность
предмету одного признака, а в другом — отрицается принадлежность этому же предмету другого признака (1) и
если речь идет о разных предметах (2).Согласно традиции этот закон принято называть законом противоречия.
Однако название — закон непротиворечия — точнее выражает его действительный смысл.

(3) Противоречия не будет и в том случае, если мы что-либо утверждаем и то же самое отрицаем относительно
одного лица, но рассматриваемого в разное время. Допустим, что обвиняемый Н. в начале следствия дал ложные
показания, однако в конце следствия он был вынужден под тяжестью изобличающих его улик признаться и дать
истинные показания. В этом случае суждения: «Показания обвиняемого Н. являются ложными» и «Показания
обвиняемого Н. являются истинными» — не противоречат друг другу.
(4) Наконец один и тот же предмет нашей мысли может рассматриваться в разных отношениях. Так, о студенте
Щукине можно сказать, что он хорошо знает немецкий язык, так как его знания удовлетворяют требованиям,
предъявленным к поступающим в институт. Однако этих знаний недостаточно для работы в качестве переводчика. В
этом случае мы вправе сказать: «Щукин плохо знает немецкий язык». В двух суждениях знание Щукиным немецкого
языка рассматривается с точки зрения разных требований, следовательно, эти суждения также не противоречат друг
другу.
Закон непротиворечия выражает одно из коренных свойств логического мышления — непротиворечивость,
последовательность мышления. Его сознательное использование помогает обнаруживать и устранять противоречия в
своих и чужих рассуждениях, вырабатывает критическое отношение ко всякого рода неточности,
непоследовательности в мыслях и действиях.
Н.Г. Чернышевский подчеркивал, что непоследовательность в мыслях ведет к непоследовательности в поступках. У
кого не уяснены принципы во всей логической полноте и последовательности, писал он, у того не только в голове
сумбур, но и в делах чепуха.Умение вскрывать и устранять логические противоречия, нередко встречающиеся в
показаниях свидетелей, обвиняемого, потерпевшего, играет важную роль в судебной и следственной практике.Одно
из основных требований, предъявляемых к версии в судебном исследовании, состоит в том, чтобы при анализе
совокупности фактических данных, на основе которых она построена, эти данные не противоречили друг другу и
выдвинутой версии в целом. Наличие таких противоречий должно привлечь самое серьезное внимание следователя.
Однако бывают случаи, когда следователь, выдвинув версию, которую он считает правдоподобной, не принимает во
внимание факты, противоречащие этой версии, игнорирует их, продолжает развивать свою версию вопреки
противоречащим фактам.В процессе судебного разбирательства обвинитель и защитник, истец и ответчик
выдвигают противоречащие друг другу положения, отстаивая свои доводы и оспаривая доводы противной стороны.
Поэтому необходимо тщательно проанализировать все обстоятельства по делу, чтобы окончательное решение суда
основывалось на достоверных и непротиворечивых фактах.Недопустимы противоречия в судебных актах. К числу
обстоятельств, по которым приговор признается несоответствующим фактическим обстоятельствам дела, уголовно-
процессуальное право относит существенные противоречия, содержащиеся в выводах суда, изложенных в приговоре.
25. Закон исключенного третьего.
Закон непротиворечия действует по отношению ко всем несовместимым друг с другом суждениям. Он
устанавливает, что одно из них необходимо ложно. Вопрос о втором суждении остается открытым: оно может быть
истинным, но может быть и ложным.Закон исключенного третьего действует только в отношении противоречащих
(контрадикторных) суждений. Он формулируется следующим образом: два противоречащих суждения не могут
быть одновременно ложными, одно из них необходимо истинно: а есть либо Ь, либо не-Ь. Истинно либо
утверждение некоторого факта, либо его отрицание.
Противоречащим (контрадикторным) называются суждения, в одном из которых что-либо утверждается (или
отрицается) о каждом предмете некоторого множества, а в другом — отрицается (утверждается) о некоторой части
этого множества. Эти суждения не могут быть одновременно ни истинными, ни ложными: если одно из них истинно,
то другое ложно и наоборот. Например, если суждение «Каждому гражданину РФ гарантируется право на получение
квалифицированной юридической помощи» истинно, то суждение «Некоторым гражданам РФ не гарантируется
право на получение квалифицированной юридической помощи» ложно. Противоречащим являются также два
суждения об одном предмете, в одном из которых что-либо утверждается, а в другом то же самое отрицается.
Например: «П. привлечен к административной ответственности» и «П. не привлечен к административной
ответственности». Одно из этих суждений необходимо истинно, другое — необходимо ложно.Этот закон можно
записать с помощью дизъюнкции: р v i p, где р — любое высказывание, "1 р — отрицание высказывания р.Подобно
закону непротиворечия закон исключенного третьего выражает последовательность, непротиворечивость мышления,
не допускает противоречий в мыслях. Вместе с тем, действуя только в отношении противоречащих суждений, он
устанавливает, что два противоречащих суждения не могут быть не только одновременно истинными (на что
указывает закон непротиворечия), но также и одновременно ложными: если ложно одно из них, то другое
необходимо истинно, третьего не дано.

Конечно, закон исключенного третьего не может указать, какое именно из данных суждений истинно. Этот вопрос
решается другими средствами. Значение закона состоит в том, что он указывает направление в отыскании истины:
возможно только два решения вопроса, причем одно из них (и только одно) необходимо истинно.
Закон исключенного третьего требует ясных, определенных ответов, указывая на невозможность отвечать на один и
тот же вопрос в одном и том же смысле и «да» и «нет», на невозможность искать нечто среднее между утверждением
чего-либо и отрицанием того же самого.Важное значение имеет этот закон в юридической практике, где требуется
категорическое решение вопроса. Юрист должен решать дело по форме «или—или». Данный факт либо установлен,
либо не установлен. Обвиняемый либо виновен, либо не виновен. Jus (право) знает только: «или—или».
26. Закон достаточного основания.
Наши мысли о каком-либо факте, явлении, событии могут быть истинными или ложными. Высказывая истинную
мысль, мы должны обосновать ее истинность, т.е. доказать ее соответствие действительности. Так, выдвигая
обвинение против подсудимого, обвинитель должен привести необходимые доказательства, обосновать истинность
своего утверждения. В противном случае обвинение будет необоснованным.
Требование доказанности, обоснованности мысли выражает закон достаточного основания: всякая мысль
признается истинной, если она имеет достаточное основание. Если есть Ь, то есть и его основание а.
Достаточным основанием мыслей может быть личный опыт человека. Истинность некоторых суждений
подтверждается путем их непосредственного сопоставления с фактами действительности. Так, для человека,
явившегося свидетелем преступления, обоснованием истинности суждения «Н. совершил преступление» будет сам
факт преступления, очевидцем которого он был. Но личный опыт ограничен. Поэтому человеку в своей деятельности
приходится опираться на опыт других людей, например на показания очевидцев того или иного события. К таким
основаниям прибегают обычно в следственной и судебной практике при расследовании преступлений.Благодаря
развитию научных знаний человек все шире использует в качестве основания своих мыслей опыт всего
человечества,закрепленный в законах и аксиомах науки, в принципах и положениях, существующих в любой области
человеческой деятельности.Истинность законов, аксиом подтверждена практикой человечества и не нуждается
поэтому в новом подтверждении. Для подтверждения какого-либо частного случая нет необходимости обосновывать
его при помощи личного опыта. Если, например, нам известен закон Архимеда (каждое тело, погруженное в
жидкость, теряет в своем весе столько, сколько весит вытесненная им жидкость), то нет никакого смысла погружать
в жидкость какой-либо предмет, чтобы выяснить сколько он теряет в весе. Закон Архимеда будет достаточным
основанием для подтверждения любого частного случая.Благодаря науке, которая в своих законах и принципах
закрепляет общественно-историческую практику человечества, мы для обоснования наших мыслей не прибегаем
всякий раз к их проверке, а обосновываем их логически, путем выведения из уже установленных положений.Таким
образом, достаточным основанием какой-либо мысли может быть любая другая, уже проверенная и
установленная мысль, из которой с необходимостью вытекает истинность данной мысли.Если из истинности
суждения а следует истинность суждения Ь, то а будет основанием для Ь, a b — следствием этого основания.Связь
основания и следствия является отражением в мышлении объективных, в том числе причинно-следственных связей,
которые выражаются в том, что одно явление (причина) порождает другое явление (следствие). Однако это
отражение не является непосредственным. В некоторых случаях логическое основание может совпадать с причиной
явления (если, например, мысль о том, что число дорожно-транспортных происшествий увеличилось,
обосновывается указанием на причину этого явления — гололед на дорогах). Но чаще всего такого совпадения нет.
Суждение «Недавно был дождь» можно обосновать суждением «Крыши домов мокрые»; след протекторов
автомобильных шил — достаточное основание суждения «В данном месте прошла автомашина». Между тем мокрые
крыши и след, оставленный автомашиной, — не причина, а следствие указанных явлений. Поэтому логическую связь
между основанием и следствием необходимо отличать от причинно-следственной связи.Обоснованность —
важнейшее свойство логического мышления. Во всех случаях, когда мы утверждаем что-либо, убеждаем в чем-либо
других, мы должны доказывать наши суждения, приводить достаточные основания, подтверждающие истинность
наших мыслей. В этом состоит коренное отличие научного мышления от мышления ненаучного, которое
характеризуется бездоказательностью, способностью принимать на веру различные положения и догмы. Это
особенно характерно для религиозного мышления, опирающегося не на доказательство, а на веру.Закон
достаточного основания не совместим с различными предрассудками и суевериями. Например, существуют нелепые
приметы:разбить зеркало — к несчастью, рассыпать соль — к ссоре и т.д., хотя между разбитым зеркалом и
несчастьем, рассыпанной солью и ссорой нет причинной связи. Логика — враг суеверий и предрассудков. Она
требует обоснованности суждений и не совместима поэтому с утверждениями, которые строятся по схеме «после
этого — значит, по причине этого». Эта логическая ошибка возникает в случаях, когда причинная связь смешивается
с простой последовательностью во времени, когда предшествующее явление принимается за причину последующего.
Закон достаточного основания имеет важное теоретическое и практическое значение. Фиксируя внимание на
суждениях, обосновывающих истинность выдвинутых положений, этот закон помогает отделить истинное от
ложного и прийти к верному выводу.

Значение закона достаточного основания в юридической практике состоит, в частности, в следующем. Всякий вывод
суда или следствия должен быть обоснован. В материалах по поводу какого-либо дела, содержащих, например,
утверждение о виновности обвиняемого, должны быть данные, являющиеся достаточным основанием обвинения. В
противном случае обвинение не может быть признано правильным. Вынесение мотивированного приговора или
решения суда во всех, без исключения, случаях является важнейшим принципом процессуального права.
27. Общая характеристика умозаключения. Виды умозаключений.
В науке и в повседневной жизни мы на каждом шагу пользуемся умозаключениями. С умозаключениями как с
определенными правилами оперирования с суждениями мы имеем дело в тех случаях, когда из данных суждений
получаем новые суждения. Выводя по правилам умозаключений из какой-либо гипотезы следствия (с целью
проверки самой гипотезы), мы имеем дело с процессом умозаключения. Заметим, что всякий раз, когда имеет место
явление а, имеет место и явление b, а когда a отсутствует и отсутствует b, мы умозаключаем, что: "Явление а есть
причина явления b".Еще более сложной формой мышления по сравнению с суждением является умозаключение. Оно
содержит в своем составе суждения (а следовательно и понятия), но не сводится к ним, а предполагает их
определенную связь. Благодаря этому и образуется качественно особая форма с ее специфическими функциями в
мышлении.
Значение анализа умозаключений определяется тем, что именно в умозаключениях (и основанных на них
доказательствах) сокрыта "тайна" принудительной силы речей, которая поражала людей еще в древности и с
постижения которой, очевидно, и началась наука логика. Именно умозаключения обеспечивают то, что мы называем
сегодня силой логики. Вот почему нередко логику именуют наукой о выводном знании. Здесь есть значительная
доля истины. Весь предшествующий анализ понятий и суждений, хотя и важный сам по себе, имеет свое значение
лишь в связи с их логическими функциями по отношению к умозаключениям (а значит, и к доказательствам и
опровержениям).Теория умозаключений - тщательно разработанная часть логики. Это очень практичная теория,
дающая мощное орудие познания и общения.Чтобы выяснить происхождение и сущность умозаключения,
необходимо сопоставить два рода знаний, которыми мы располагаем и пользуемся в процессе своей
жизнедеятельности - непосредственные и опосредованные.
Непосредственные знания - это те, которые мы получаем с помощью органов чувств. Это знания, выраженные
суждениями типа: "Глина желтая"; "Пыль серая"; "Собака лает"; "Морская вода соленая". Они составляют
значительную часть всех наших знаний и служат основой их развития.Однако далеко не обо всем на свете мы можем
судить непосредственно. Никто, например, не видел, что в районе пустыни Сахары ранее было море. А знание об
этом существует. Каким же образом? Оно получено из других знаний путём умозаключений.Знания, которые
получены не прямо, непосредственно, а опосредованно, путем выведения из других знаний, называются
опосредованными (или выводными). Логической формой их приобретения служит умозаключение. Это - форма
мышления, посредством которой из известного знания выводится новое знание.
Существование такой формы в нашем мышлении, как и понятия и суждения, обусловлено самой объективной
действительностью. Если в основе понятия лежит предметный характер действительности, а в основе суждения -
связь или отношение предметов, принадлежность им признаков, то, что же составляет объективную основу
умозаключения? Объективную основу умозаключения составляет сложная взаимосвязь предметов, их взаимные
отношения. Так, если один класс предметов С входит целиком в другой D, но не исчерпывает его объема, то это
означает необходимую обратную связь: более широкий класс предметов D включает в себя менее широкий С как
свою часть, но не сводится к нему.
"Все летчики - мужественные люди". Это означает: "Некоторые мужественные люди -
летчики". Или более сложный случай взаимосвязи предметов мысли: если один класс
предметов С входит в другой D, а этот в свою очередь входит в третий Е, то отсюда
следует, что первый С входит в третий Е. Схема:
Если Петр Николаевич Нестеров был летчиком, а все летчики - мужественные люди,
то П.Н. Нестеров был мужественным человеком.
C D E Умозаключения - распространенная форма, которая используется в научном и повседневном
мышлении. Этим определяется их роль в познании и практике общения людей.
Значение умозаключений состоит в том, что они не только связывают наши знания в достаточно сложные,
относительно сформированные комплексы - мыслительные конструкции, но и обогащают, углубляют эти
знания.Вместе с понятиями и суждениями умозаключения преодолевают ограниченность и недостатки чувственного
познания.Они оказываются незаменимыми там, где органы чувств бессильны: в постижении причин и условий
возникновения какого-либо предмета или явления, его сущности и форм существования, закономерностей развития.
Умозаключения участвуют в образовании понятий и суждений, которые нередко выступают как итог
умозаключений, чтобы стать средствами дальнейшего познания. Умозаключения используют как способ познания
прошлого, которое непосредственно наблюдать нельзя. Умозаключения важны для понимания будущего, которое
наблюдать еще нельзя. Особую роль умозаключения играют в юридической практике. В современной юридической
c
D
C
c
D
E
D
D

литературе и практике умозаключениям принадлежит исключительная роль. Так, предварительное следствие, с
точки зрения логики, есть не что иное, как построение всевозможных умозаключений: 1) о предполагаемом
преступнике, 2) о механизме образования следов преступного деяния, 3) о мотивах, побудивших к его совершению и
4) о последствиях совершенного для общества. Сам суд есть не что иное, как анализ фактов с целью получения
определенного вывода. Наконец, обвинительное заключение есть лишь одна из форм умозаключения.
Структура умозаключения обусловлена природой этой формы мышления. В структуре умозаключения различают
два основных более или менее сложных элемента: посылки (одна или несколько) и заключение, между которыми,
конечно, существует определенная связь.Посылки - это исходное, уже известное знание, служащее основанием для
умозаключения.Заключение (или вывод) - производное и притом новое знание, полученное из посылок и
выступающее их следствием. Связь между посылками и умозаключением есть необходимое отношение между ними,
делающее возможным переход от одного к другому, - отношение логического следования. Если мы признаем какие-
либо посылки, то мы вынуждены признать и заключение – именно из-за определенной связи между тем и другим, а
также между самими посылками. Это закон, в основе которого лежит объективное соотношение самих предметов
мысли, он проявляется во многих особых правилах, которые специфичны для разных видов умозаключений.
Если рассматривать процесс познания диалектически, как процесс перехода с одной ступени знания на другую,
более высокую, то станет ясным относительность деления суждений на посылки и заключение. Одно и то же
суждение, будучи выводом одного познавательного акта, становится посылкой другого. Как строительство дома -
например, один ряд бревен, положенный на уже имеющееся основание, превращается тем самым в основание для
другого - последующего ряда.Подобно всякому суждению заключение может быть истинным и ложным.
Заключение будет истинным при двух условиях:
1) если посылки истинны по содержанию;
2) если умозаключение правильно по своей форме.
Все поэты тонко чувствуют природу.
Ф.И. Тютчев - поэт.
Следовательно, Ф.И. Тютчев тонко чувствовал природу.
Здесь обе посылки истинны, а умозаключение построено правильно, что видно
из схемы: А - Ф.И. Тютчев, В - поэты, С - тонко чувствующие природу.
И наоборот заключение может быть ложным, если:
1) хотя бы одна посылка ложна;
2) строение умозаключения неправильное.
Например: Все свидетели правдивы.
Попцов - свидетель.
Следовательно, Попцов правдив.
Здесь одна из посылок ложна, поэтому определенного вывода сделать нельзя. Из ложных посылок или при
неправильном строении умозаключения истинным вывод может получиться чисто случайно.
Например: Стекло не проводит электричества.
Медь - не стекло.
Следовательно, медь проводит электричество.
При таком строении умозаключения достаточно вместо "меди" подставить "дерево", чтобы понять случайность
верного вывода. Связь между посылками и заключением должна быть не случайной, а необходимой, однозначной,
обоснованной: одно должно действительно следовать, вытекать из другого. Нельзя построить хороший дом, если,
например, в наличии лишь плохой материал - гнилые бревна, но и дом из качественного материала может
развалиться, если его строить неправильно, неумело, не соблюдать определенных законов.
Как и любая другая форма мышления, умозаключение, так или иначе воплощается в языке. Если понятие выражается
отдельным словом или словосочетанием, а суждение отдельным предложением или сочетанием предложений, то
умозаключение всегда есть связь нескольких (двух или более) предложений; хотя не всякая связь двух или более
предложений - обязательно умозаключение (вспомнить хотя бы сложные суждения).В русском языке эта связь
выражается словами "следовательно", "значит", "таким образом" и другими.Употребление тех или иных языковых
средств не произвольно, а определяется порядком расположения посылок и заключения. В живой речи, в отличие от
учебника по логике, этот порядок тоже является относительным. Умозаключение может завершаться заключением,
но может и начинаться с него; наконец, вывод может находиться в середине умозаключения - между посылками.
И это естественно, ведь новизна заключения не психологическая, а логическая. Она не носит характера какой-то
счастливой случайности или озарения, когда из произвольного сочетания каких-то суждений вдруг что-то
получилось. И новизна эта, конечно, не заложена ни в одном из элементов исходного знания, но потенциально,
скрыто содержится в структуре этого знания в целом и проявляется лишь во взаимодействии ее элементов. Общее
правило языкового выражения умозаключения таково: Если заключение стоит после посылок, то перед ним ставятся
A
З
н
а
ч
е
н
и
е
у
м
о
за
к
л
ю
ч
е
н
и
й
с
о
ст
о
и
т
в
т
о
м
,
ч
т
о
о
н
и
н
е
т
о
л
ь
к
о
с
в
яз
ы
в
а
ю
т
н
а
ш
и
з
н
а
н
и
я
в
д
о
с
та
т
о
ч
н
о
с
л
о
ж
н
ы
е,
о
т
н
о
с
и
т
е
л
ь
н
о
с
ф
о
р
м
и
р
о
в
а
н
н
ы
е
к
о
м
п
л
е
к
с
ы
-
м
ы
с
л
и
т
е
л
ь
н
ы
е
к
о
н
с
т
р
у
к
ц
и
и,
н
о
и
о
б
о
га
щ
а
ю
т,
уг
л
у
б
л
я
ю
т
эт
и
з
н
а
н
и
я.
В
м
е
с
т
е
с
п
о
н
я
т
и
я
м
и
и
с
у
ж
д
е
н
и
я
м
и
у
м
о
за
к
л
ю
ч
е
н
и
я
п
р
е
о
д
о
л
е
в
а
ю
т
о
г
р
а
н
и
ч
е
н
н
о
с
т
ь
и
н
е
д
о
с
та
т
к
и
ч
у
в
с
т
в
е
н
н
о
г
о
п
о
з
н
а
н
и
я.
c
