Шпаргалка к кандидатскому минимуму по мат.методам
Подождите немного. Документ загружается.


значение – нулю.
Современные пакеты статистического анализа для ПЭВМ позволяют
найти все
s
решений характеристического уравнения и получить тем самым
систему коэффициентов канонической корреляции.
На каждом шаге анализа помимо коэффициента канонической
корреляции и канонических коэффициентов (весов) первичных признаков –
)1()1(
2
)1(
1
,,,
s
CCC
и
)2()2(
2
)2(
1
,,,
tsss
CCC
– полезно вычислить:
а) канонические нагрузки, т . е . коэффициенты корреляции каждого из
s
признаков результатов с канонической переменкой
)1(
Z
и каждого из
t
признаков факторов с канонической переменной
)2(
Z
;
б) квадраты канонических нагрузок, как характеристики вклада
канонической переменной
)1(
Z
в общую вариацию системы
s
первичных
признаков результатов, а для канонической переменной
)2(
Z
– ее вклада в
вариацию системы
t
первичных признаков факторов;
в) перекрестные канонические нагрузки, как оценка парной корреляции
первичных признаков результатов с канонической
переменной
)2(
Z
, а для признаков факторов – их корреляции с
канонической переменной
)1(
Z
.
Для первого цикла расчетов (т. е. для максимальной канонической
корреляции) полезно получить результаты проверки исходной совокупности
факторных признаков на возможность их исключения из дальнейшего
анализа. Проверка на возможность исключения (проверка на избыточность
системы факторных признаков) выполнима, если количество факторных
признаков, включенных в исследование, больше, чем число признаков
результатов, т.е.
ts
. Суть проверки сводится к тому, что из начальной
совокупности
t
факторов исключается с последующим возвратом каждый
признак.
Для каждого варианта такого исключения сообщаются:
коэффициент канонической корреляции
s
признаков результатов с
оставшимися
)1( t
признаками факторами;
коэффициент частной корреляции исключаемого факторного признака с
системой
s
признаков результатов, при условии, что часть дисперсии
многомерного признака результата уже объяснена системой
)1( t
признаков факторов;
частное значение
F
-статистики, показывающее, насколько увеличилось
бы полное значение
F
-статистики, если бы в совокупность
)1( t
признаков
факторов был возвращен данный признак
Если число зависимых переменных равно 1, то процедура проверки
факторных признаков на исключение из системы может быть полезна как
инструмент отбора признаков регрессоров при построении регрессионной
модели. В принципе, при известных канонических множителях и
единственной переменной в совокупности признаков результатов
)1( s
не
сложно рассчитать параметры уравнения множественной линейной регрессии,
поскольку максимальный коэффициент канонической корреляции в этом
случае равен обычному коэффициенту множественной линейной корреляции.
Но гораздо удобнее с этой целью использовать стандартный модуль
регрессионного анализа.
Анализ канонической корреляции обычно весьма трудоемок и сложен
Поэтому, несмотря на исключительную важность результатов такою анализа,
даже простейшая иллюстрация расчета требует использования ПЭВМ.
Т8 2. Основные понятия устойчивых методов оценки.
Методы оценивания, учитывающие наличие "грубых ошибок" и
позволяющие при этом достаточно точно определять оценки параметров,
называются робастными или устойчивыми.
При обработке экономической информации, как правило, считают, что
экономические показатели подчиняются нормальному распределению.
Однако практика обработки такой информации показывает, что
экономические показатели не так часто подчиняются теоретическому
нормальному распределению. Наблюдаются отклонения как односторонние,
так и двухсторонние, когда "хвосты" дифференциального закона
оказываются более тяжелыми, чем можно было предположить, исходя из
данных таблиц нормального распределения. Иногда статистическая
информация по данному показателю представляет собой смесь нескольких
законов распределения с разными дисперсиями. Встречаются смеси
основного нормального распределения с распределениями других видов.
Наблюдаются случаи, когда из-за малого объема выборки не представляется
возможным достаточно точно определить вид закона, засоряющего
распределения. Кроме того, хорошо известно, что при применении метода
наименьших квадратов небольшое число грубых ошибок может существенно
исказить значение характеристик распределения. Следовательно, необходимо
остановиться на таких методах обработки экономической информации,
которые были бы менее чувствительными к виду закона распределения и
влиянию небольшого числа больших случайных отклонений.
Исключение грубых ошибок из рассмотрения приводит к уменьшению
количества точек наблюдения и не дает нужного результата. Поэтому
необходимы были методы, позволяющие анализировать "засоренные"
данные.
Основы робастных методов оценки экономической информации были
разработаны академиками А.Н.Колмогоровым, Н.В.Смирновым и
Б.С.Ястремским. Дальнейшее развитие робастные методы получили в
работах американского статистика Д.Тьюки и швейцарского математика
Хубера. В настоящее время создан целый раздел прикладной математической
статистики, включающий методы устойчивого оценивания показателей,
подчиняющихся различным законам распределения. В современной науке
используется несколько робастных методов оценки экономической
информации.
При определении структуры неоднородных совокупностей здесь
возникают две задачи. Первая задача заключается в разбиении общей
неоднородной совокупности на некоторое число однородных совокупностей,

а вторая – в оценке параметров совокупностей, которые содержат грубые
ошибки.
При решении первой задачи необходимо:
классифицировать элементы по однородным совокупностям;
оценить параметры распределения однородных составляющих, входящих
в общую неоднородную совокупность.
При решении второй задачи чаще используются методы
непосредственного выявления грубых ошибок и методы, которые сводят к
минимуму искажения, создаваемого грубыми ошибками, а также
комбинированные методы, которые выделяют грубые ошибки и дают
наиболее правдоподобную оценку параметров распределения, не
искаженную грубыми ошибками.
Пусть совокупность вместе с "обычными" значениями элементов
содержит "грубые ошибки". Таким образом, основная масса элементов
является реализациями случайной величины, закон распределения которой
известен с точностью до некоторого параметра. Вероятность появления этих
элементов в совокупности равна
1
, где
– вероятность появления другой
случайной величины –
, определяющей грубые ошибки.
Процедуры, предусмотренные теорией нормальных ошибок, не
устойчивы к "грубым" ошибкам. Более устойчивыми оказываются
процедуры, связанные с определением средней абсолютной ошибки.
Известен целый ряд методов исключения резко выделяющихся наблюдений.
Наиболее доступным и распространенным является анализ измерений с
точки зрения экономической сущности полученных наблюдений. Для
выявления резко выделяющихся наблюдений имеется ряд критериев,
которые являются несмещенными, инвариантными по отношению к
преобразованиям совокупности и требуют добавления константы или
умножения каждого члена совокупности на положительное число.
Для критериев Граббса и Смирнова-Граббса получены точные
распределения и их процентные точки. Они служат для выявления отдельных
выделяющихся наблюдений. Для обнаружения нескольких экстремальных
наблюдений используют критерий Титьена-Мура, который выявляет
"маскирующий эффект", имеющий место, когда в совокупности находятся
два и более близких экстремальных значений случайной величины.
В экономических исследованиях очень важно выявить грубые ошибки
при построении регрессионных моделей, проведении многомерного
стохастического анализа.
Т8 3. Методы обнаружения засорения (грубые ошибки)
1) Метод выявления грубых ошибок Смирнова-Граббса
Проверка максимального наблюдения
Пусть
N
xxx ,,,
21
результаты наблюдения. По полученным
наблюдениям построим вариационный ряд
)()2()1( N
xxx
.
Если известны среднее квадратическое отклонение
и
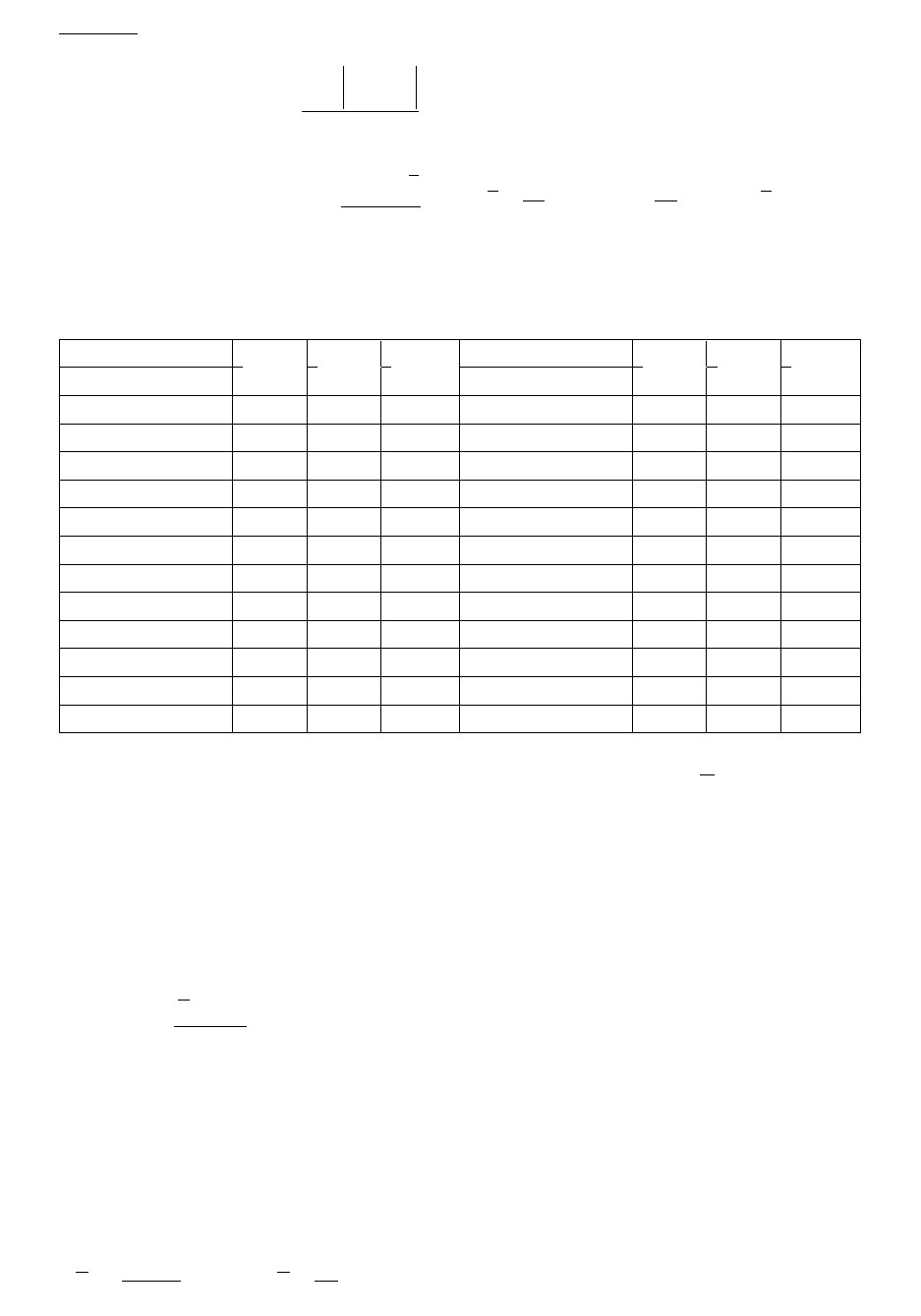
математическое ожидание
, то можно воспользоваться критерием
)(
)(
N
N
x
t
и сравнить его с данными таблицы процентных точек критерия
Смирнова-Граббса
)(
max
max
i
x
i
t
.
Если же
и
неизвестны, то необходимо воспользоваться табл. 8.1. Для
этого надо определить
s
x
N
x
N
T
)(
)(
, где
N
i
x
i
x
N
s
N
i
i
x
N
x
1
2
)(
1
2
;
1
1
.
Затем сравнить значение
)(N
T
с
C
из табл. 8.1.
Таблица 8.1
Таблица Граббса. Критические значения
C
№ наблюдения
10,0
05,0
025,0
№ наблюдения
10,0
05,0
025,0
1 - - - 14 2,297 2,461 2,602
2 - - - 15 2,326 2,493 2,638
3 1,406 1,412 1,414 16 2,354 2,523 2,670
4 1,645 1,689 1,710 17 2,380 2,551 2,701
5 1,791 1,869 1,917 18 2,404 2,577 2,728
6 1,894 1,996 2,067 19 2,426 2,600 2,754
7 1,974 2,093 2,182 20 2,447 2,623 2,778
8 2,041 2,172 2,273 21 2,467 2,644 2,801
9 2,097 2,237 2,349 22 2,486 2,664 2,823
10 2,146 2,294 2,414 23 2,504 2,683 2,843
11 2,190 2,353 2,470 24 2,520 2,701 2,862
12 2,229 2,387 2,519 25 2,537 2,717 2,880
13 2,264 2,426 2,562 26 2,553 2,734 2,897
Если
CT
N
)(
, то верна гипотеза
0
H
о том, что
)(N
x
не является грубой
ошибкой. При
CT
N
)(
,
)(N
x
значимо отклоняется от
x
, следовательно,
является грубой ошибкой. Встречаются таблицы, где используется вместо
понятие доверительной вероятности
, где
1
и, тогда критическое
значение
1
CC
;
C
соответствует величине
)(N
T
при гипотезе
0
H
,
отвечающей доверительной вероятности
)(
)(
CTP
N
.
Проверка минимального наблюдения
Проведем проверку гипотезы Н
0
с альтернативной Н, при помощи
критерия
)(1
)1(
)1(
min;
i
i
xx
s
xx
T
.
Если
0
H
верна, то
)1(
T
имеет такое же распределение, как и
)(N
T
,
поэтому для проверки гипотезы можно воспользоваться табл.9.8.
2) Критерий Граббса для обнаружения одного
экстремального
наблюдения
Пусть дан ряд наблюдений
N
xxx ,,,
21
, по которому построен
вариационный ряд
)()2()1(
,,,
N
xxx
и получены оценки
;
1
1
1
1
)(1
N
i
i
x
N
x
N
i
i
x
N
x
1
)(
1
.
Для проверки максимального значения на наличие грубой ошибки

используется критерий
N
i
i
N
i
i
N
xx
xx
G
1
2
)(
1
1
2
1)(
)(
)(
.
Если надо проверить минимальное значение, то применяется критерий
N
i
i
N
i
i
xx
xx
G
1
2
)(
1
2
1
)(
1
)(
)(
, где
N
i
i
x
N
x
2
)(
1
1
1
.
Критические значения
C
для критериев
)1(
G
, и
)(N
G
можно
определить по табл. 8.2.
Наблюдения
)1(
x
или
)(N
x
относят к грубым ошибкам, если
наблюдаемые значения статистик
1
G
или
)(N
G
окажутся больше
критического.
Таблица 8.2
Критические значения
C
при использовании критериев
)1(
G
, и
)(N
G
№ наблюдения
10,0
05,0
025,0
№ наблюдения
10,0
05,0
025,0
1 - - - 14 0,5942 0,5340 0,4792
2 - - - 15 0,6134 0,5539 0,5030
3 0,0109 0,0027 0,0007 16 0,6306 0,5755 0,5246
4 0,0975 0,0494 0,0248 17 0,6461 0,5933 0,5442
5 0,1984 0,1270 0,0808 18 0,6601 0,6095 0,5621
6 0,2826 0,2032 0,1453 19 0,6730 0,6243 0,5785
7 0,3503 0,2696 0,2066 20 0,6848 0,6379 0,5937
8 0,4050 0,3261 0,2616 21 0,6958 0,6504 0,6076
9 0,4502 0,3742 0,3101 22 0,7058 0,6621 0,6206
10 0,4881 0,4154 0,3526 23 0,7151 0,6728 0,6327
11 0,5204 0,4511 0,3901 24 0,7238 0,6829 0,6439
12 0,5483 0,4822 0,4232 25 0,7319 0,6923 0,6544
13 0,5727 0,5097 0,4528
3) Критерий исключения нескольких грубых ошибок
Подход Титьена-Мура – обобщение критерия Граббса на несколько
экстремальных наблюдений.
Пусть по выборке объемом
N
построен вариационный ряд
)()2()1( N
xxx
.
Тогда решающее правило для отношения
k
наибольших наблюдений к
грубым ошибкам основано на статистике
N
i
i
kN
i
ki
k
xx
xx
L
1
2
)(
1
2
)(
)(
)(
)(
, где
kN
x
x
kN
i
i
k
1
)(
,
где
k
x
– средняя арифметическая
)( kN
наблюдений после отбрасывания
k
наибольших наблюдений;
x
– выборочная средняя арифметическая всей
выборки.
Решающее правило для отнесения
k
наименьших наблюдений к грубым
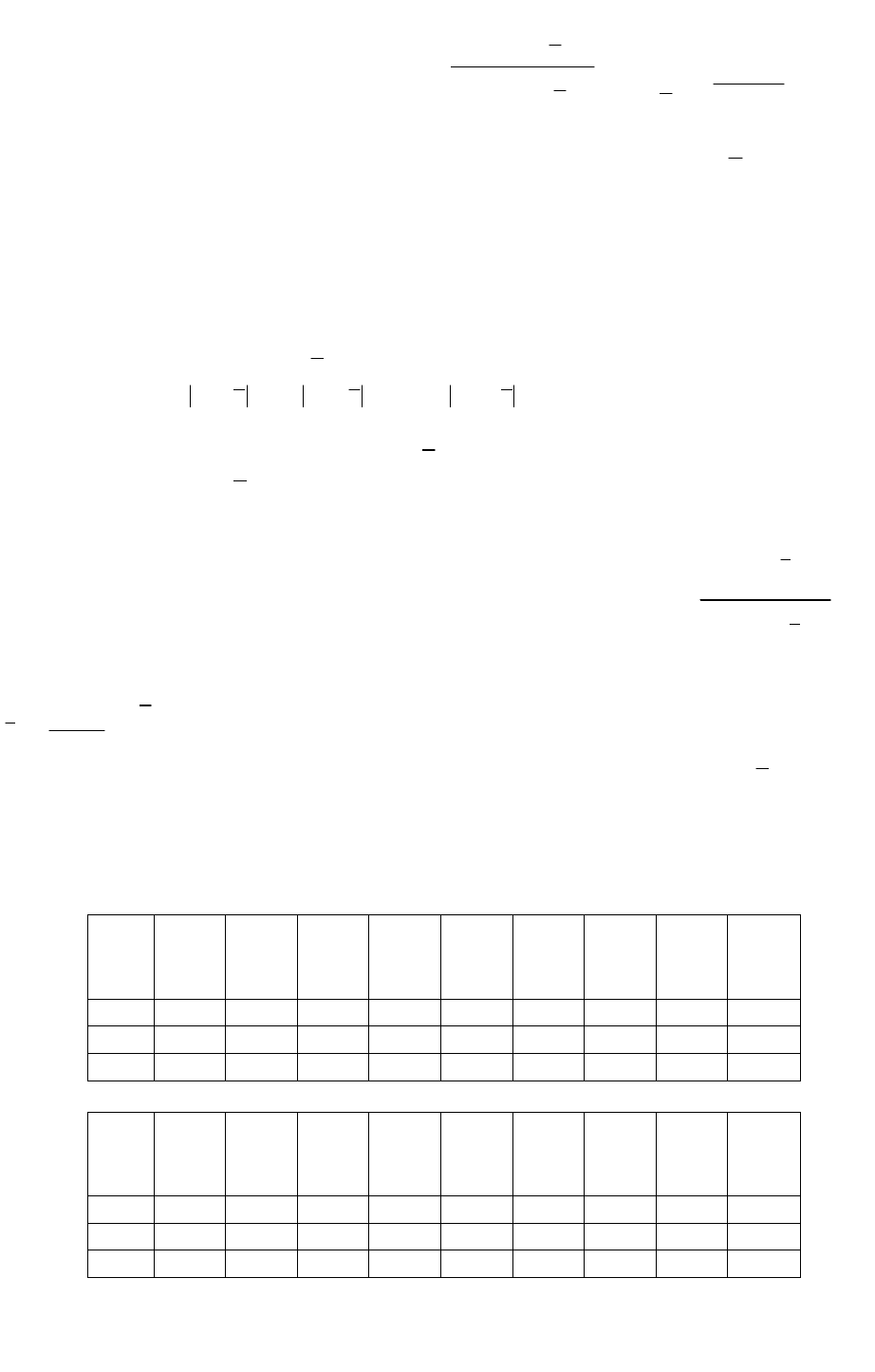
ошибкам основано на статистике
N
i
i
N
ki
k
i
k
xx
xx
L
1
2
)(
1
2
)(
)(
)(
)(
~
, где
kN
x
x
N
ki
i
k
1
)(
, где
)( kN
– число наибольших наблюдений в выборке;
k
x
– средняя
арифметическая
)( kN
наблюдений после удаления из выборки
k
наименьших наблюдений.
)1(
L
– эквивалентна
)(N
G
, а
)1(
~
L
– величине
)1(
G
.
4) Критерий обнаружения экстремальных наблюдений (наибольших и
наименьших) одновременно.
При помощи алгоритма метода по выборке вычисляется среднее
арифметическое значение
x
и производится расчет абсолютных отклонений
от среднего:
xxrxxrxxr
NN
,,,
2211
.
Строится возрастающий ряд с переиндексацией:
i
z
– наблюдение
i
r
–
i
-е по величине. Самое близкое к
x
значение обозначим
1
z
, а через
N
z
–
самое удаленное от
x
наблюдение.
Для проверки гипотезы о том, что
k
наибольших по модулю наблюдений
являются грубыми ошибками, используется величина:
N
i
i
kN
i
ki
k
zz
zz
E
1
2
1
2
)(
)(
)(
)(
, где
kN
z
z
kN
i
i
k
1
; (
)(k
z
– средняя арифметическая из
)( kN
наблюдений, оставшихся
после исключения из выборки
k
подозрительных элементов);
z
– средняя
арифметическая всей выборки.
Критические значения для
)(k
E
даны в табл. 8.3.
Таблица 8.3
Значения
C
для
)( k
E
)05,0(
n
k
3 4 5 6 7 8 9 10 11
1 0,001 0,125 0,081 0,146 0,208 0,265 0,314 0,356 0,386
2 - 0,001 0,010 0,034 0,065 0,099 0,137 0,172 0,204
3 - - - 0,04 0,016 0,034 0,057 0,083 0,107
n
k
12 13 14 15 16 17 18 19 20
1 0,424 0,455 0,484 0,509 0,526 0,544 0,562 0,581 0,597
2 0,234 0,262 0,293 0,317 0,340 0,362 0,382 0,397 0,416
3 0,133 0,165 0,179 0,206 0,227 0,248 0,267 0,287 0,302
Значение
)(k
E
сравнивается с критическим значением
C
. Если
CE
k
)(
, то
k
рассматриваемых наблюдений являются грубыми ошибками.

Содержание по темам:
Т1 1. Основные экономико-статистические показатели и соответствующие
между ними взаимосвязи.
Т1 2. Многомерное признаковое пространство. Особенности обработки
многомерных статистических данных.
Т2 1. Понятие многомерного статистического анализа.
Т2 2. История возникновения и развития МСА.
Т2 3. Предмет и метод КСА.
Т2 4. Классификация методов МСА.
Т2 5. Характеристика методов МСА.
Т2 6. Этапы проведения МСА.
Т3 1. Основные понятия корреляционного анализа.
Т3 2. Двумерная модель корреляционного анализа.
Т3 3. Основные понятия регрессионного анализа.
Т3 4. Оценка параметров регрессии. Проверка адекватности
регрессионной модели.
Т4 1.Общая характеристика методов кластерного анализа
Т4 2. Меры сходства в кластерном анализе
Т4 3. Иерархический кластерный анализ
Т4 4. Итеративные методы кластерного анализа
Т6 1. Классификация с обучением
Т6 2. Линейный дискриминантный анализ
Т6 3. Алгоритм дискриминантный анализа
Т7 1. Сущность компонентного анализа
Т7 2. Математическая модель метода главных компонент
Т7 3.Алгоритм метода главных компонент
Т8 1. Анализ канонической корреляции.
Т8 2. Основные понятия устойчивых методов оценки.
Т8 3. Методы обнаружения засорения (грубые ошибки)
