Шпаргалка к кандидатскому минимуму по мат.методам
Подождите немного. Документ загружается.


1) предполагает пересчет центра тяжести кластера после каждого изменения
его состава;
2) лишь после того, как будет завершен пересмотр всех данных.
В обоих случаях итеративный алгоритм этого метода минимизирует внутри
каждого кластера.
Т6 1. Классификация с обучением
Дискриминантный анализ как раздел многомерного статистического
анализа включает в себя статистические методы классификаций
многомерных наблюдений ситуаций, когда исследователь наблюдает так
называемыми обучающими выборками (классификация с «учителем»). В
общем случае задача различения (дискриминаций) формулируется
следующим образом. Пусть результатом наблюдения над объектом является
реализация К-мерного случайного вектора:
Х=(Х
1
, Х
2
,…Х
n
)
T
.
Требуется установить правила согласно которому по наблюдаемому
значению вектора Х объект относят к одной из возможных совокупностей П
i
I=1,2,3,…l. Для построения правила дискриминации всё выборочное
пространство R значений вектора Х разбивается на области R
i
=(1,2,..l). Так
что при попадании Х в R
i
объект относят к совокупности П
i
. Правило
дискриминации выбирается в соответствии с определенным принципом
оптимальности. На основе априорной информации о совокупности Р
i
извлечение объекта из П
i
при этом следует учитывать размер убытка от
неправильной дискриминации. Априорная информация может быть
представлена либо в виде некоторых сведений, а функции К-мерного
распределения признаков в каждой совокупности либо в виде выборов из
совокупностей.
Постановка задачи дискриминантного анализа в случае когда исходная
информация о распределении представлена выборка из них (наиболее важная
ситуация в дискриминантном анализе).
Пусть Х
1
(i)
, Х
2
(i)
,…Х
J
(i)
,…Х
ni
(i)
выборка совокупностей П
i
i=(1,l), j=(1,n
i
).
Причем каждый j объект выборки представлен К-мерным вектором
параметров:
X
J
(i)
=(X
i1
(i)
, X
i2
(i)
,…,X
iq
(i)
,….,X
ik
(i)
)
Произведено дополнительное наблюдение Х=(Х
1
,…,Х
к
)
т
над объектом,
который принадлежит одной из совокупностей П
i
. Требуется построить
правило отношения наблюдения Х к одной из этих совокупностей.
Обычно в задаче различения переходят от вектора-признака,
характеризующий объект линейной функции от них, дискриминантные
функции – гиперплоскости, наилучшим образом разделяющей совокупность
выборочных точек.
Т6 2. Линейный дискриминантный анализ(ЛДА)
Предположения линейного ДА
1) имеются различные классы объектов.
2) Каждый класс имеет нормальную функцию плотности от К
переменных X=(X
1
,X
2
,…,X
ni
)
T
.
Функция плотности:
)()(
2
1
exp()2()(
)(
1
)(
2
1
2
i
i
T
i
i
ni
xExEПxf
µ
(i)
- вектор переменных-матожиданий размерности К
Е
i
– ковариационная матрица при n-n
i
Матрица Е
i
положительно определена. Если параметры известны, то
дискриминация проводится следующим образом: имеются функции
плотности f
1
(x), f
2
(x),…, f
n
(x) в нормально распределенных классах.
Задана точка Х в пространстве К измерений. Параметры многомерного
нормального распределения
ˆ
,
ˆ
могут быть оценены по выборочным
данным. Задано l выборок: (Х
1
(1)
,Х
2
(2)
,…,Х
n
(i)
)=X
i
li ,1
из некоторых классов.
Математические ожидания µ
1
,µ
2
,…,µ
к
могут быть определены
средними значениями:
i
n
j
i
iq
i
i
X
n
q
1
)()(
1
kq ,1
несмещенные оценки ковариационной матрицы Е:
i
n
j
i
r
i
jr
i
r
i
ir
i
rs
i
xx
n
E
1
)()()()(
))(
ˆ
(
1
1
)
ˆ
(
ksr ,1,
оценки µ
i
и E
i
определяется по l выборкам в каждом классе.
Получив оценки, точки Х отнесем к классу, для которого функция f(x)
максимальна. Предположим, что все классы, среди которых должна
проводится дискриминация, имеют нормальное распределение с одной и той
же ковариационной матрицы Е.
Тогда класс, к которому должна принадлежать точка Ч, можно определить на
основе неравенства:
f
i
(x)>f
j
(x)
Если Е
J
=E
i
=E, а µ
I
– вектор мат.ожиданий класса I, то можно
представить неравенство в их квадратичных формах:
-[(X-µ
(i)
)
T
E
-1
(X-µ
(i)
)]>-[(X-µ
(J)
)
T
E
-1
(X-µ
(J)
)]
раскроем скобки:
-(X
T
E X-X
T
E
-1
µ
(i)
–µ
(i)T
E
-1
X+µ
(i)T
E
-1
µ
(i)
)>-(X
T
E
-1
X-X
T
E
-1
µ
(J)
-µ
(J)T
E
-1
X+µ
(J)T
E
-1
µ
(J)
учитывая, что скалярное произведение двух векторов Z и W можно
записать:
Z
Т
W=W
Т
Z=(Z,W) – общий вид (правило)
Исключим справа и слева выражение Х
Т
Е
-1
Х и поменяем знаки:
Х
Т
Е
-1
Х+µ
(J)T
Е
-1
Х=2(Х
Т
Е
-1
µ
(J)
)=2(ХЕ
-1
µ
(J)
);
µ
(J)T
E
-1
µ
(J)
=(µ
(J)
,E
-1
µ
(J)
анлогично преобразование по i. Сократив обе части неравенства на 2 и
используя запись квадратичных форм, получим:
(XE
-1
µ
(i)
)-1/2(µ
(i)
,E
-1
µ
(i)
)>(XE
-1
µ
(i)
)-1/2(µ
(i)
,E
-1
µ
(i)
)
обозначим:
)(
1
i
i
i=
m,1
)(
1
)(
,
2
1
ii
i
mi ,1
Тогда (*) имеет вид:
i
ii
XX
)()(
,,
3
Проверенная точка Х относится к классу I для каждой линейной функции
вида :
max),()(
)(
i
Xxh
i
i
Преимущества линейной дискриминации заключаются в линейности
дискриминантной функции и надежности оценок ковариационных матриц.
Т6 3. Алгоритм дискриминантного анализа
1. определение оценки ковариационных матриц:
i
ki
S
x
S
y
ki
S
y
S
1
1
1
n
i
ijj
X
m
X
k
X
j
X
k
X
i
X
m
k
X
ik
X
ij
X
ij
X
n
S
i
kj
1
1
1
3,2,1k
j
X
,
k
X
- средние значение
2. рассчитывается несмещенная оценка суммарной ковариационной матрицы:
yx
SnSn
nn
S
21
21
2
1
ˆ
;
3. определение обратной матрицы к несмещенной оценке:
1
ˆˆ
SS
;
4. вычисление вектора оценок коэффициентов дискриминантной функции:
yxSa
1
ˆ
;
5. рассчитывает оценок векторов значений дискриминантной функции для
матрицы исходных данных:
a
X
x
U
ˆ
,
a
Y
y
U
ˆ
;
6. вычисление средних значений оценок дискриминантной функции:
1
1
1
1
ˆ
n
i
xi
U
n
x
U
2
1
2
1
ˆ
n
i
yi
U
n
y
U
;
7. Определение константы
С
y
U
x
UС
ˆˆ
2
1
ˆ
Дискриминантная функция для
U
-го наблюдения подлежащего
дискриминации получаем решив уравнение:
303202101
0
azazazU

xCU
ˆ
ˆ
0
yCU
ˆ
ˆ
0
Если
СU
ˆ
ˆ
0
,то -ое наблюдение относится к совокупности
х
;
Если
СU
ˆ
ˆ
0
, то -ое наблюдение относится к совокупности
Т7 1. Сущность компонентного анализа
Метод главных компонент является одним из методов факторного
анализа. Длительное время метод главных компонент (компонентный анализ)
рассматривался многими авторами как одна из разновидностей факторного
анализа. При этом под факторным анализом понимался способ приведения
множества наблюдаемых непосредственно признаков к меньшему числу
неявных, но объективно существующих факторов. В настоящее время метод
главных компонент часто отделяют от факторного анализа. Впервые он был
предложен К. Пирсоном в 1901г., затем развит, доработан, описан и
обоснован в работах Г. Хотеллинга, Г. Хармана, С. Рао, П. Андруковича, С.А.
Айвазяна и др.
В нашей стране метод главных компонент стал распространяться с
появлением ЭВМ вследствие удобства математических процедур и наличия
стандартных программ, которые оказалось возможным применить для
организации математического обеспечения алгоритма расчета. Метод
главных компонент обладает определенными преимуществами перед
другими методами факторного анализа. Он не требует, например, никаких
гипотез о переменных, является линейным и аддитивным.
Несмотря на то, что при методе главных компонент надо для точного
воспроизведения коэффициентов корреляции между переменными найти все
n
компонент, большая доля изменчивости признаков (дисперсии)
объясняется небольшим числом
)(m
компонент. Кроме того, при методе
главных компонент можно по признакам описать компоненты, а по
компонентам – признаки. К тому же метод главных компонент одинаково
хорошо приближает дисперсии и ковариации.
Метод главных компонент считается статистическим методом, но есть
подход, не являющийся статистическим. Этот подход связан с получением
наилучшей проекции совокупности точек наблюдения в пространство
меньшей размерности. В этом случае надо знать матрицу вторых моментов.
При статистическом подходе задача заключается в выделении линейных
комбинаций случайных величин, имеющих максимально возможную
дисперсию. Общим между статистическим и нестатистическим подходом
является использование матрицы вторых моментов как исходной для начала
анализа. Из вышесказанного следует, что для овладения методом главных
компонент необходимо пользоваться методами теории вероятностей и
математической статистики на основе моделей линейной алгебры.
Несмотря на то, что при решении поставленной задачи вместо
n
признаков может быть получено такое же количество главных компонент,

вклад большей части главных компонент в объясняемую дисперсию
оказывается небольшим. Исключаем из рассмотрения те главные
компоненты, вклад которых мал. Оказывается, что при помощи
m
первых
(наиболее весомых) главных компонент можно объяснить часть суммарной
дисперсии.
Опыт исследования в различных областях показал, что число наиболее
весомых компонент зачастую составляет 10-25% числа признаков. В
зависимости от конкретных задач решается вопрос о том, сколько и каких
компонент следует оставить для дальнейшего исследования: одну, две, 25%
общего числа извлеченных или более. В связи с этим часто используется
понятие объясняемой групповой дисперсии, при помощи которой проводится
содержательная интерпретация полученных результатов. Для экономической
интерпретации полученных результатов самыми наглядными являются
случаи, когда
32,1 илиm
. Таким образом, можно сделать выводы.
1. Метод главных компонент позволяет описать большие наборы признаков
n
небольшим числом главных компонент
)( nmm
;
2. Различия между объектами зависят от доли изменчивости, связанной с
данной главной компонентой;
3. Каждому признаку свойственна факторная структура;
4. Связи между признаками и факторами (главными компонентами) –
линейные;
5. Для данного признака эффект воздействия факторов суммируется.
Т7 2. Математическая модель метода главных компонент
Модель метода главных компонент записывается следующим образом:
n
j
r
jr
j
f
a
y
1
, где
f
r
–
r
-я главная компонента;
a
jr
– вес
r
-й
главной компоненты на
j
-й переменной;
y
j
– центрированное
(нормированное) значение
j
-го признака.
Множество главных компонент представляет собой удобную систему
координат, а соответствующие дисперсии главных компонент характеризуют
их статистические свойства.
Главные компоненты являются характеристическими векторами
ковариационной матрицы (это покажем ниже).
Множество главных компонент представляет собой удобную систему
координат, а соответствующие дисперсии главных компонент характеризуют
их статистические свойства.
Важным в компонентном анализе является получение матрицы
весовых коэффициентов.
Теорема. Для любой симметрической положительно определенной
матрицы
R
существует ортогональная матрица
U
, такая, что

n
T
RUU
00
00
00
2
1
, а все элементы матрицы
положительны
)0(
r
, определитель матрицы
R
положителен
0R
, все главные миноры
матрицы положительны. При этом:
r
– собственное значение, или
характеристический корень матрицы
R
;
n
21
.
Воспользуемся
U
и
для получения матрицы нагрузок
A
. Составим
характеристическое уравнение
0 ER
. (6.1)
Проведем преобразования с помощью матрицы
U
и получим:
n
j
j
n
TT
EERUUUERU
1
2
1
)(
00
00
00
)(0
. (6.2)
Значит, характеристические корни матрицы
R
совпадают с
диагональными элементами преобразованной матрицы.
Воспользуемся основными уравнениями метода главных компонент
для ненормированных признаков
j
x
:
ii
Afx
, (6.3)
nijnijijji
fafafax
2211
, (6.4)
где
ji
x
– центрированное значение изучаемого признака;
ri
f
–
r
-я главная компонента у
i
-го объекта исследования;
jr
a
– весовой коэффициент
r
-й главной компоненты;
N
– число объектов;
n
– число признаков.
В матричном виде выражение (6.3) запишется
11
FAX
, (6.5)
если
X
является матрицей центрированных значений переменных.
Если взять нормированные значения переменных – матрицу
Y
, то
получим выражение
AFY
. (6.6)
Размерности матриц:
X
и
Y
)( Nn
,
A
и
1
A
)( nn
,
F
и
1
F
)( Nn
.
При извлечении всех главных компонент матрица весовых
коэффициентов будет квадратной порядка
n
.
Признаки, составляющие матрицу
X
или
Y
, подчинены нормальному
закону распределения, как и главные компоненты. Следовательно,
взаимосвязи между признаками определяются ковариационной матрицей
.
Она является симметрической матрицей, на главной диагонали которой стоят
дисперсии признаков, а внедиагональные элементы представляют собой
ковариации.

Введем ортогональную матрицу
U
и перейдем вместо переменных
x
к новым переменным
z
причем
Uzx
xUz
T
, (6.7)
где
z
z
z
z
2
1
,
nj ,1
;
x
– вектор центрированных значений параметров (6.7)
иллюстрирует связь между переменными
x
и
z
; вектор
r
u
–
r
-й столбец
ортогональной матрицы
U
;
T
r
u
– вектор-строка в матрице
T
U
.
Вектор выбирается таким образом, чтобы дисперсия была
максимальной. После получения вектора выбирается вектор
2
u
таким
образом, чтобы дисперсия
2
z
была максимальной при условии, что
2
z
не
коррелирует с
1
z
. Процедура проводится для любого
r
z
так, чтобы
дисперсия максимальной при условии отсутствия корреляции со всеми
переменными
1
,,
2
,
1 r
zzz
. Обозначим невырожденную ковариационную
матрицу через
, а дисперсию
r
z
через
r
. Тогда
x
T
r
u
r
z
, а
r
–
собственное значение, которому соответствует собственный вектор
r
u
. Тогда
запишем характеристическое уравнение
0)(
rr
uE
или
r
u
rr
u
. (6.8)
Слева умножим обе части равенства на
T
r
u
:
r
u
r
T
r
u
r
u
T
r
u
.
Так как у ортогональных матриц
1
r
u
T
r
u
, то
r
u
T
r
u
r
, а так как
r
z
не
коррелированны, то при
sr
0
s
u
T
r
u
.
Это значит, что
UU
T
(6.9)
является диагональной матрицей с элементами
n
21
.
r
является
собственным значением собственного вектора
r
u
.
Проведя нормирование
r
z
, получим
r
-ю главную компоненту
r
f
. При
нормировании
r
z
дисперсии должны равняться единицам для всех индексов
nr ,1
при переменных
r
z
.
Дисперсия исследуемых признаков в методе главных компонент.
Главные компоненты ортогональны между собой, поэтому полная
дисперсия
j
-го признака равна
1
1
22
n
r
jr
a
j
, где
2
jr
a
– доля полной
дисперсии
j
-го признака, вносимая
r
-й главной компонентой.
На практике извлекают только часть главных компонент, равную
nm
.
Оставляют наиболее весомую часть главных компонент, вкладом остальных
)( mn
компонент в этом случае пренебрегают, так как каждая из
)( mn
главных компонент вносит малую долю в общую дисперсию изучаемого
процесса.

Тогда вместо
n
r
r
f
jr
a
j
y
1
имеем
m
r
r
f
jr
a
j
y
1
.
Полный вклад всех
m
извлеченных главных компонент в общую
дисперсию всех признаков равен
m
r
r
V
1
0
, а относительный вклад
0
1
V
n
K
,
где
K
– показатель факторизации в методе главных компонент.
Т7 3. Алгоритм метода главных компонент
Одним из методов исследования зависимостей между признаками
является метод главных компонент, содержание которого состоит в
приведении множества наблюдаемых признаков к меньшему числу неявных,
но объективно существующих факторов. Процесс нахождения главных
компонент удобно представить в виде алгоритма.
Алгоритм метода главных компонент
1. Формирование матрицы исходных данных
)(
ji
xX
,
njNi ,,1;,,1
,
где
N
– число наблюдаемых объектов,
n
– число измеряемых признаков,
n
ji
x
– зарегистрированное значение измеряемого признака
j
у
i
-го
объекта.
2. Нормирование элементов матрицы исходных данных. В результате
получаем матрицу
Y
порядка
Nn
, элементами которой являются
нормированные значения
j
-го признака для
i
-го объекта –
ji
y
.
3. Определение матрицы наблюденных коэффициентов корреляции. Она
является исходной для проведения анализа и представлена в следующем
виде:
N
YYR
1
,
где
Y
– матрица нормированных значений признаков,
Y
–
транспонированная матрица.
4. Вычисление собственных значений матрицы
R
, которые располагаются в
порядке убывания
0
21
n
, и соответствующий им ортогональный
базис из собственных векторов
n
uuu ,,,
21
.
5. Из полученных векторов конструируется ортогональная матрица
),,,(
21 n
uuuU
, связывающая признаки и факторы.
6. Ранжирование факторов по убыванию дисперсий
n
zzz
21
. Более
важным считается тот фактор, у которого больше дисперсия. Если главный
фактор
f
m 1
вносит малую долю дисперсии
1m
в общую дисперсию
признаков
n
i
i
n
1
, то им и дальнейшими факторами
ff
nrm
,,
пренебрегают и считают что явление приближенно описывается факторами
fff
m
,,,
21
. При этом, конечно, теряется дисперсия
n
i
i
n
1
.
7. Определение матрицы весовых коэффициентов
A
:
2
1
UA
,
где
– диагональная матрица, элементами которой являются собственные
значения матрицы
R
.
8. Определяется вклад
r
-го фактора в дисперсию всех
n
признаков. Он
определяет ту долю общей дисперсии, которую данная главная компонента
объясняет. Этот вклад вычисляется по формуле:
V
r
=
n
j
jr
a
1
2
,
где
j
– индекс признака,
r
– индекс фактора,
a
jr
- элементы матрицы
A
.
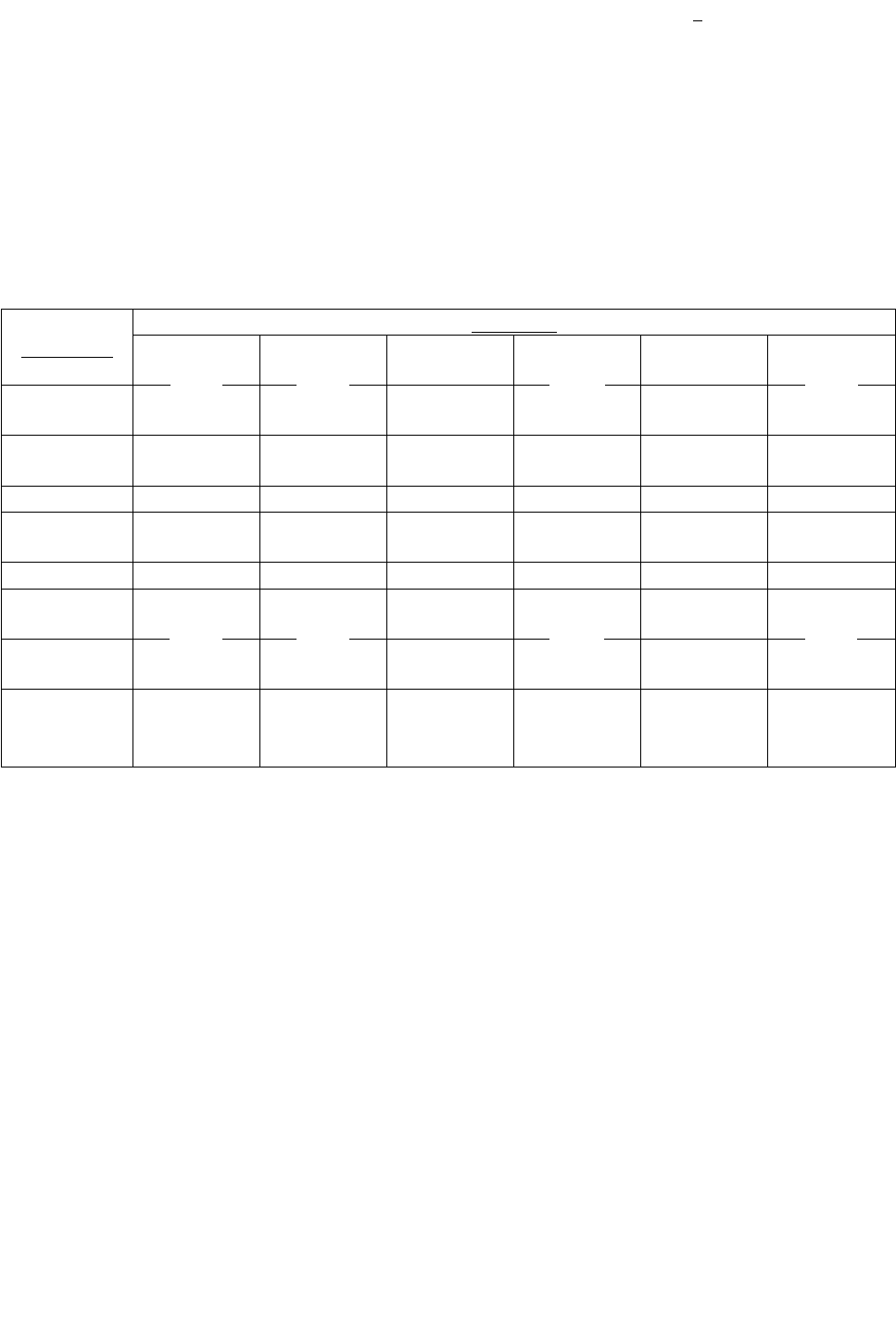
9. Строится таблица результатов, полученных методом главных компонент:
Признаки
Факторы
F
1
F
2
. . .
F
m
. . .
F
n
1
a
11
a
12
. . .
a
m1
. . .
a
n1
2
a
21
a
22
. . .
a
m2
. . .
a
n2
. . . . . . . . . . . . . . . . . . . . .
j
a
j1
a
j 2
. . .
a
jm
. . .
a
jn
. . . . . . . . . . . . . . . . . . . . .
n
a
n1
a
n2
. . .
a
nm
. . .
a
nn
V
r
Процент
Суммарной
Дисперсии
Главными компонентами считаются факторы с высоким процентом
суммарной дисперсии.
10. Интерпретация полученных результатов.
Т8 1. Анализ канонической корреляции.
Посредством анализа канонической корреляции оценивается
взаимосвязь между двумя группами первичных показателей. Первую группу
образуют зависимые признаки или признаки результаты. Вторую группу
образуют признаки независимые или признаки причинные. Иногда их
называют признаками факторами, хотя с точки зрения факторного анализа это
обычные первичные показатели. Таким образом, если общее число признаков
изучаемой системы равно
m
, то из них (например, в качестве гипотезы)
выделяют:
s
признаков результатов и
t
признаков факторов.
Для реализации процедуры канонической корреляции следует
выполнить условия:
mtsts ;
Таким образом, можно считать, что матрица
R
парной линейной

корреляции оказывается состоящей из блоков
2221
1211
RR
RR
R
Здесь
11
R
– подматрица корреляции признаков результатов, размерность этой
матрицы
ss
;
12
R
– подматрица корреляции признаков результатов с признаками
факторами, размерность этой матрицы
ts
;
21
R
– транспонированная подматрица корреляции признаков результатов с
признаками факторами, размерность этой матрицы
st
;
22
R
– подматрица корреляции признаков факторов, размерность этой
матрицы
tt
.
Максимальный корень
характеристического уравнения
0)det(
21
1
2212
1
11
2
RRRRE
является искомой оценкой канонической
корреляции двух исходных совокупностей признаков (
s
-результатов и
t
-
факторов).
Для максимального значения
составляется система линейных
однородных уравнений
0
)2(
)2(
1
)1(
)1(
2
)1(
1
2221
1211
ts
s
s
C
C
C
C
C
RR
RR
Вектор
C
решения этой системы представляет совокупность
канонических множителей для первой группы признаков (результатов)
),,,(
)1()1(
2
)1(
1 s
CCC
,
и для второй группы признаков (факторов)
),,,(
)2()2(
2
)2(
1 tsss
CCC
.
Эти коэффициенты позволяют перейти от
s
-мерной совокупности
наблюдений по признакам результатам к одномерной совокупности по
признаку
)1(
Z
ss
YCYCYCZ
)1(
2
)1(
21
)1(
1
)1(
, и от
t
-мерной совокупности
наблюдений по признакам факторам к одномерной совокупности по
признаку
)2(
Z
ttsss
XCXCXCZ
)2(
2
)2(
21
)2(
1
)2(
Парный линейный коэффициент корреляции одномерных признаков
)1(
Z
и
)2(
Z
оказывается равным
.
Так как все математические операции производятся с матрицей
R
, то
значения одномерных признаков
)1(
Z
и
)2(
Z
должны определяться, если в
этом возникает потребность, по стандартизованным первичным данным:
дисперсия каждого из
)( ts
признаков должна быть равна 1. а среднее
