Шпаргалка к кандидатскому минимуму по мат.методам

Подождите немного. Документ загружается.

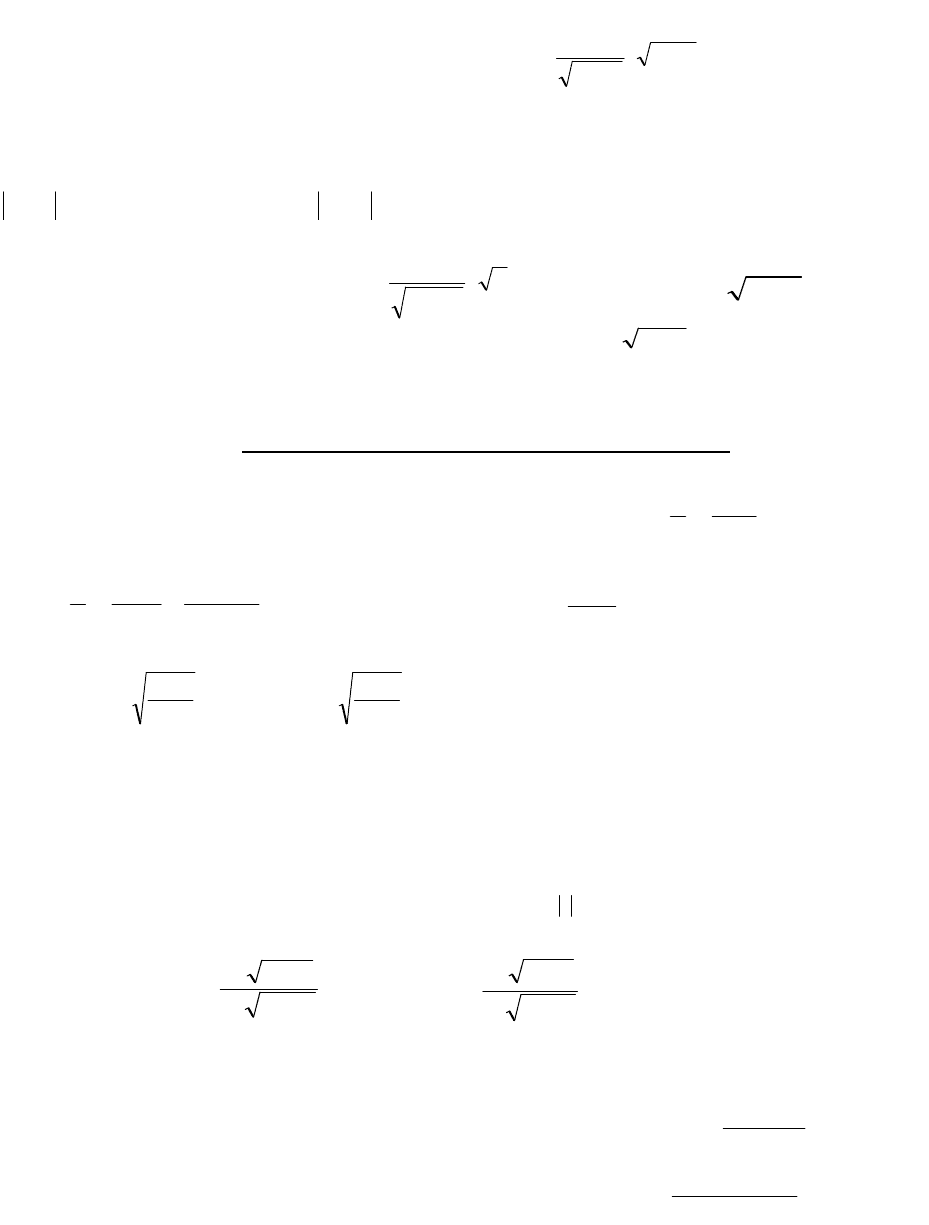
Статистика

, вычисляемая для выборки из двумерной нормально

распределенной совокупности с

0



, связана со статистикой

(Стьюдента)

2n



степенями свободы, формулой





 n

. Зная границы для

, соответствующие соответствующим уровням значимости (

%1%,2%,5%,10



), можно получить границы для

, воспользовавшись

этой формулой. Границы для

табулированы. Находим

табл

. Если

табл

набл

r 

, то

0



; если

табл

набл

r 

, то

0



При

100



пользуются нормированным нормальным законом

распределения

-статистики









1 r

или статистики

1nr

Если наблюдаемая величина (

или

1nr

) расположена в

доверительном интервале

 







, то принимается гипотеза о

0



иначе – гипотеза отвергается с уровнем значимости



Интервальные оценки параметров связи.

При нахождении доверительного интервала для коэффициента

корреляции



используют статистику Фишера:







, которая при

10n

распределена приблизительно нормально с генеральным средним

)1(21













и дисперсией





. Тогда доверительный

интервал, оценивающий

с надежностью



1

имеет вид







tzMz

rrr





– находится по таблице интеграла

Лапласа.

Для перехода от



есть таблица, составленная Фишером и Иейтсом,

после использования которой получаем интервальную оценку с надежностью



вида

maxmin

rr 



. Если коэффициент корреляции значим, то

коэффициенты регрессии также значимо отличаются от нуля. Интервальные

оценки для них получают по формулам:

),(



tt 

2n



– степени

свободы;

)(

yxbt







;

)(

xybt







где

имеет распределение Стьюдента с

2n



степенями свободы.

Для значимого коэффициента корреляции



некоторые авторы

рекомендуют более предпочтительную оценку, чем

















)4(2

Предпочтительной оценкой



является выражение

1)1(





Этими точечными оценками следует пользоваться при небольших

объемах выборки

Т3 3. Основные понятия регрессионного анализа.

После того, как с помощью корреляционного анализа выявлено

наличие статистически значимых связей между переменными и оценена

степень их тесноты, переходят обычно к математическому описанию

конкретного вида зависимостей с использованием регрессионного анализа.

С этой целью подбирают класс функций, связывающих результативный

показатель

и аргументы

xxx ,,,



, отбирают наиболее информативные

аргументы, вычисляют оценки неизвестных значений параметров уравнения

связи и анализируют точность полученного результата.

Функция

),,,(

21 n

xxxf 

, описывающая зависимость условного среднего

значения результативного признака

от заданных значений аргументов,

называется функцией (уравнением) регрессии.

С целью наилучшего восстановления по исходным статистическим

данным условного значения результирующего показателя

)(xy

неизвестной функции регрессии

)(xf

наиболее часто используют следующие

критерии адекватности (функции потерь).

1). Метод наименьших квадратов, согласно которому минимизируется

квадрат отклонения наблюдаемых значений результативного показателя

от модельных значений

),(



xfy 

, где

),,(





– коэффициенты

уравнения регрессии,

– значения вектора аргументов в

-м наблюдении.







min

)

(



)



xfy 

Решается задача отыскания оценки



вектора



. Получаемая регрессия

называется среднеквадратической.

2). Метод наименьших модулей, согласно которому минимизируется

сумма абсолютных отклонений наблюдаемых значений результативного

показателя от модельных значений



min

),( 







Получаемая регрессия называется среднеабсолютной (медианной).

3). Метод минимакса сводится к минимизации максимума модуля

наблюдаемого значения результативного показателя

от модельного

значения

),(



, т.е.



min),(

max 



xfy

Получаемая регрессия называется минимаксной.

В практических приложениях часто встречаются задачи, в которых

изучается случайная величина у, зависящая от некоторого множества

переменных

и неизвестных параметров

),0(, mj





Будем рассматривать

),,,,(

21 n

xxxy 

как

)1( m

-мерную генеральную

совокупность, из которой взята случайная выборка объемом

, где

),,,,(

21 iniii

xxxy 

результат

-го наблюдения

ni ,1

. Требуется по

результатам наблюдений оценить неизвестные параметры

),0( mj





Описанная задача относится к задачам регрессионного анализа.

Регрессионным анализом называется метод статистического анализа

зависимости случайной величины

от переменных

),1( mjx



рассматриваемых в регрессионном анализе как неслучайные величины,

независимо от истинного закона распределения

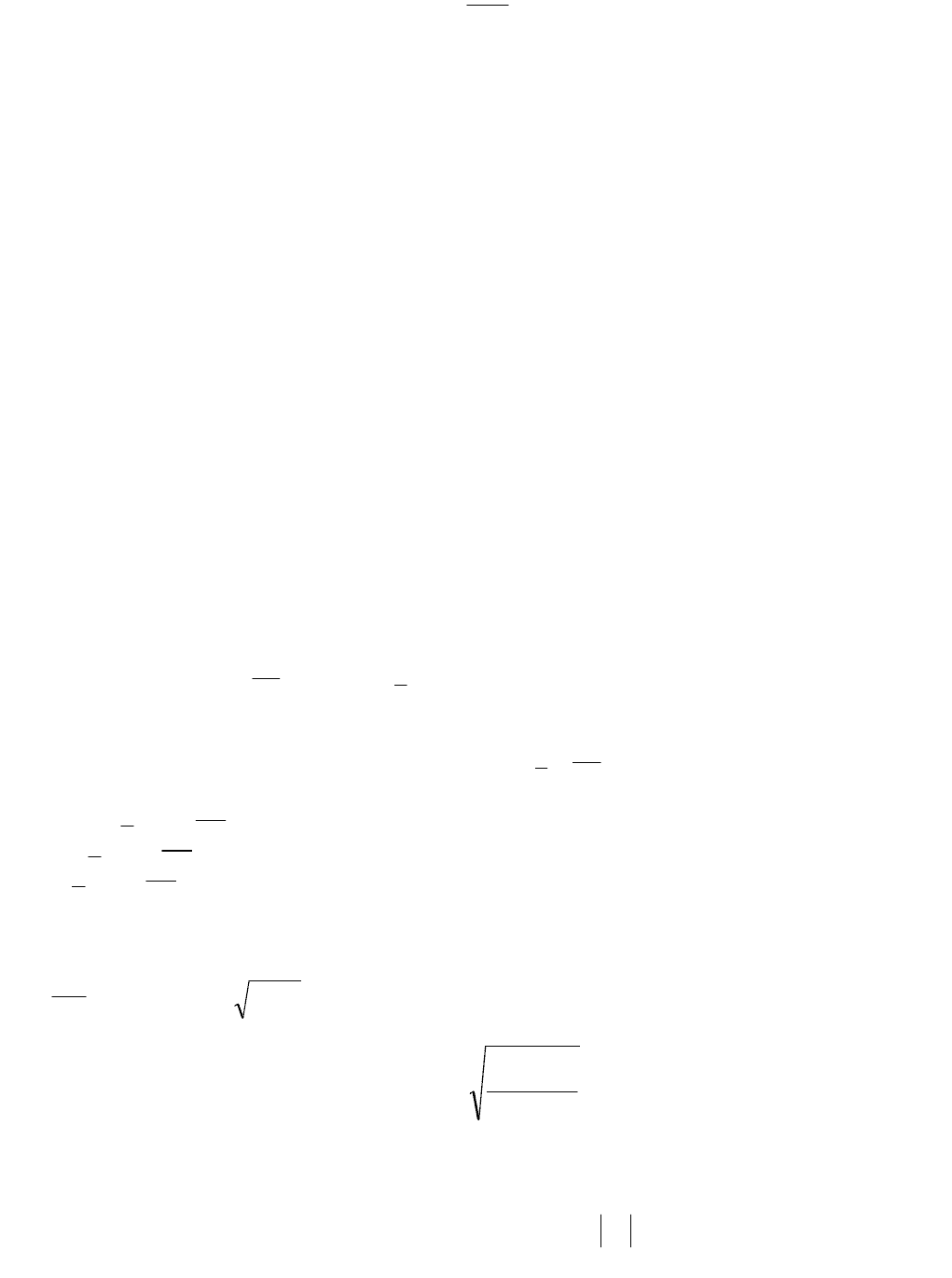
Обычно предполагается, что случайная величина

имеет нормальный

закон распределения с условным математическим ожиданием

, которое

является функцией от аргументов

),1( mjx



и постоянной, не зависящей от

аргументов дисперсией



Требование нормальности закона распределения

необходимо лишь

для проверки значимости уравнения регрессии и его параметров



, а также

интервального оценивания



. Для получения точечных оценок



это

условие не требуется.

Т3 4. Оценка параметров регрессии. Проверка адекватности

регрессионной модели.

xaxaxaay  

22110

Оценка параметров регрессии с использованием метода наименьших

квадратов.

Строится система нормальных уравнений, решив которую получают

значения параметров модели.















immmmmm

imm

yxxaxxaxxaxa

yxxxaxxaxaxa

yxaxaxana

22111

11212

1110

22110







или в матричной форме: матрица коэффициентов при



















112

mmmm

xxxxxx

xxxn







;

вектор правых частей



















;

),,,(

10 m

aaaa 

В матричной форме система имеет вид:

YXaB 

Решение с помощью обратной матрицы:

YXBa

YXBaE

YXBaBB







Существенность влияния фактора

на

проверяется с помощью

критерия Стьюдента (статистическая значимость параметров модели):

t 

, где

1



SBS

– среднеквадратическая ошибка или оценка

среднеквадратического отклонения,







– среднеквадратическое

отклонение,

iii

yye



1

– диагональный элемент матрицы

1

сравнивается с табличным значением

табл

для уровня значимости



1 mnk

степеней свободы. Если

табл

tt 

, говорят о

существенном влиянии

-го фактора на результативный признак, в

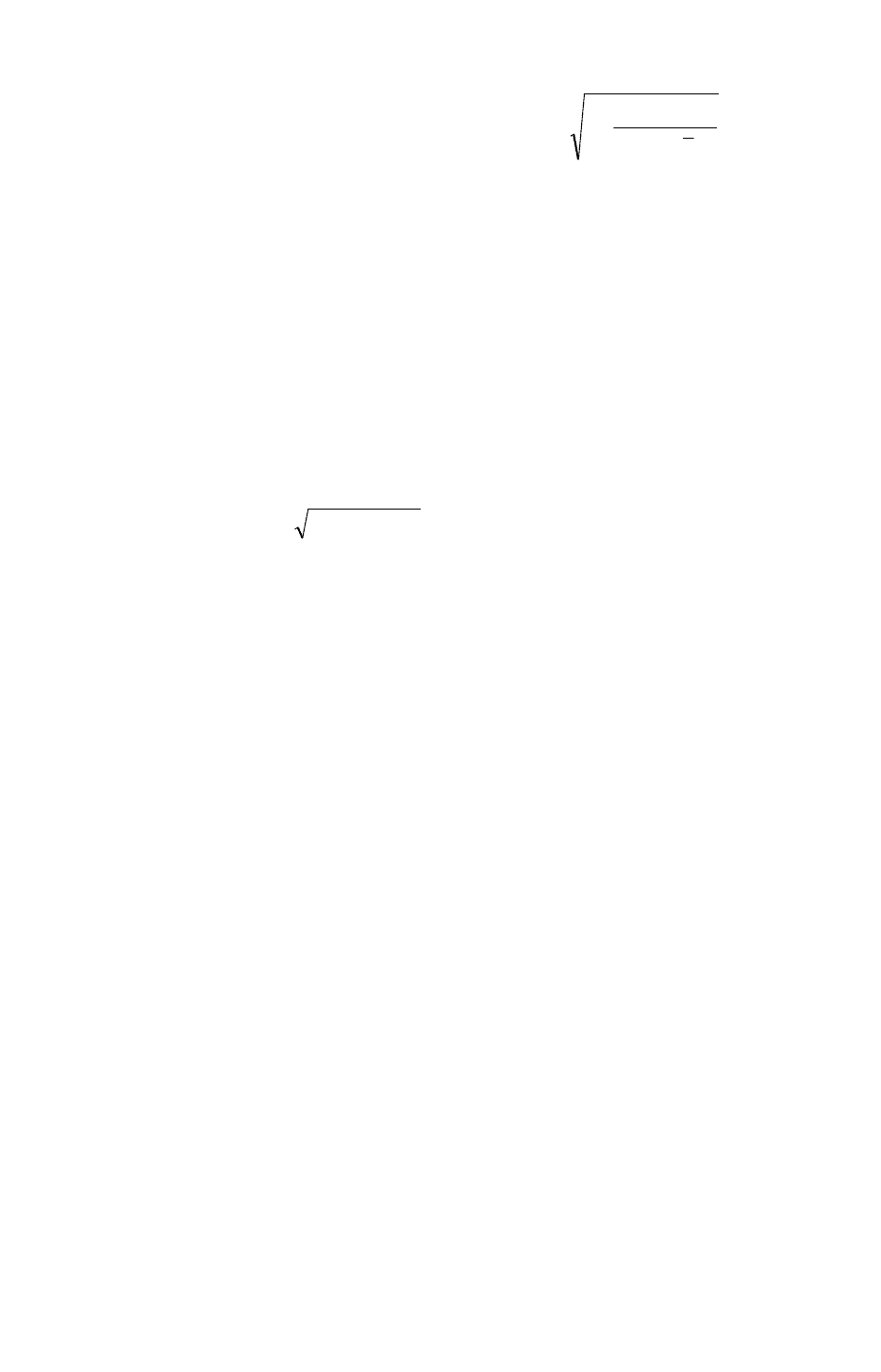
противном случае

-й фактор оказывает незначительное влияние на

результативный и его исключают из модели.

Для оценки подобранной линейной модели используют

множественный коэффициент корреляции

)(

)

(





Коэффициент детерминации

Rd 

Если

1R

, то модель адекватна; если

75,0R

, то модель можно

использовать для прогноза.

Прогнозирование экономических явлений с помощью полученной

модели.

xaxaxaay  

22110

Пусть имеются признаки

пр

xxx

пр

,,,



, которые назовем

прогнозными. Тогда

пр

xaxaxaay

прпрпр

 

Доверительные интервалы для прогнозного значения:

прпрпрпрпр

yyyyy 

табл

пр

Sty 

XBXS





),,,,1(

пр

прпр

xxxX 

Т4 1 .Общая характеристика методов кластерного анализа

Одним из направлений статистического исследования является

кластерный анализ. Особо важное место он занимает в тех отраслях науки,

которые связаны с изучением массовых явлений и процессов. Методы

кластерного анализа помогают построить научно обоснованные

классификации, выявить внутренние связи между единицами наблюдаемой

совокупности. Кроме того, методы кластерного анализа могут

использоваться с целью сжатия информации, что является важным

фактором в условиях постоянного увеличения и усложнения потоков

статистических данных.

Кластерный анализ — это совокупность методов, позволяющих

классифицировать многомерные наблюдения, каждое из которых

описывается набором исходных переменных Х

, Х

, ..., Х

Целью кластерного анализа является образование групп схожих

между собой объектов, которые принято называть кластерами. Слово

кластер английского происхождения (cluster), переводится как сгусток,

пучок, группа. Родственные понятия, используемые в литературе, — класс,

сгущение.

Кластерный анализ приводит к разбиению на группы с учетом всех

группировочных признаков одновременно участвовавших в группировке, то

есть они учитываются все сразу при отнесении наблюдения в ту или иную

группу. При этом не указаны четкие границы каждой группы, а также

неизвестно заранее, сколько групп целесообразно выделить в исследуемой

совокупности.

Можно выделить две основные причины для развития методов

многомерного анализа:

1) необходимость классификации в различных областях знаний;

2) развитие вычислительной техники.

Методы кластерного анализа позволяют решать следующие задачи:

• проведение классификации объектов с учетом признаков, отражающих

сущность, природу объектов. Решение такой задачи, как правило, приводит к

углублению знаний о совокупности классифицируемых объектов;

• проверка выдвигаемых предположений о наличии некоторой структуры в

изучаемой совокупности объектов, т.е. поиск существующей структуры;

• построение новых классификаций для слабоизученных явлений, когда

необходимо установить наличие связей внутри совокупности и попытаться

привнести в нее структуру.

Методы кластерного анализа можно разделить на две группы:

1) агломоративные (объединяющие) – последовательно объединяют

отдельные объекты в группу (кластеры).

2) дивизимные методы (разделяющие) – расчленяют группу на

отдельные объекты.

В свою очередь каждый метод может быть реализован при помощи

различных алгоритмов. Кроме того, в кластерном анализе существуют

методы, которые трудно отнести к первой или второй группе, например,

итеративные методы.

В частности метод k-средних и метод поиска сгущений. Их

особенность состоит в том, что кластеры формируются исходя из заданных

условий разбиения (параметров), которые в процессе работы алгоритма

могут быть изменены пользователем для достижения желаемого качества

разбиения.

Итеративные методы относятся к быстродействующим, что позволяет

использовать их для обработки больших массивов исходной информации.

В отличии от агломоративных и дивимных методов итеративные

алгоритмы могут привести к образованию пересекающихся кластеров, когда

один и тот же объект может одновременно принадлежать нескольким

кластерам.

Для удобства записи формализованных алгоритмов кластерного

анализа введем следующие условные обозначения:

, Х

, ..., Х

— совокупность объектов наблюдения;

=(X

i2,

… X

) — i-е многомерное наблюдение в т-мерном

пространстве признаков (i = 1, 2, ..., п);

dij — расстояние между i-м и j-м объектами;

zij — нормированные значения исходных переменных;

D — матрица расстояний между объектами.

Т4 2. Меры сходства в кластерном анализе

Для проведения классификации необходимо ввести понятие сходства

объектов по наблюдаемым переменным. В каждый кластер (класс, таксон)

должны попасть объекты, имеющие сходные характеристики.

В кластерном анализе для количественной оценки сходства вводится

понятие метрики. Сходство или различие между классифицируемыми

объектами устанавливается в зависимости от метрического расстояния

между ними. Если каждый объект описывается k признаками, то он может

быть представлен как точка в k-мерном пространстве, и сходство с другими

объектами будет определяться как соответствующее расстояние.

В кластерном анализе используются различные меры расстояния

между объектами:

1) евклидово расстояние:







)(

2) взвешенное евклидово расстояние:







)(

3) расстояние cite-blok:







2) расстояние Минковского:

)

||(







3) расстояние Махаланобиса: dij = (Xi-Xj)’S

-1

(Xi-Xj),

где dij — расстояние между i-м и j-м объектами;

xil, xjl — значения l-й переменной соответственно у i-го и j-го объектов;

Хi Xj — векторы значений переменных у i-го и j-го объектов,

— общая ковариационная матрица;

wk — вес, приписываемый k:-й переменной.

Оценка сходства между объектами сильно зависит от абсолютного

значения признака и от степени его вариации в совокупности. Чтобы

устранить подобное влияние на процедуру классификации, можно значения

исходных переменных нормировать одним из следующих способов:







max



z 

min



Выбор меры состояния и весов для классифицируемых переменных

очень важный этап кластерного анализа. От этих процедур зависят состав и

количество формируемых кластеров, а также степень сходства объектов

внутри кластера.

Если алгоритм кластеризации основан на измерении сходства между

переменными, то в качестве мер сходства могут быть использованы:

• линейные коэффициенты корреляции;

• коэффициенты ранговой корреляции;

• коэффициенты контингенции и т. д.

В зависимости от типов исходных переменных выбирается один из

видов показателей, характеризующих близость между ними.

Т4 3. Иерархический кластерный анализ

К наиболее распространенным в экономике относят иерархические и

итеративные.

Сущность иерархических агломеративных методов заключается в том,

что на первом шаге каждый объект выборки рассматривается как отдельный

кластер. Процесс объединения кластеров происходит последовательно: на

основании матрицы расстояний или матрицы сходства объединяются

наиболее близкие объекты. Если матрица сходства первоначально имеет

размерность т х т, то полностью процесс кластеризации завершается за т—

1 шагов, в итоге все объекты будут объединены в один кластер.

Последовательность объединения легко поддается геометрической

интерпретации и может быть представлена в виде графа-дерева (денд-

рограммы). На дендограмме указываются номера объединяемых объектов и

расстояние или иная мера сходства, при которой произошло объединение.

Множество методов иерархического кластерного анализа различается

не только используемыми мерами сходства (различия), но и алгоритмами

классификации. Из них наиболее распространены метод одиночной связи,

метод полных связей, метод средней связи, метод Уорда.

Алгоритм иерархического кластерного анализа

1) значения исходных переменных нормируются

2) рассчитанная матрица расстояний или мер сходства

3) находится пара самых близких кластеров. По выбранному алгоритму

объединяются эти два кластера. К новому кластеру присваивается меньший

номер объединенного кластера.

4) процедуры 2,3,4 повторяются до тех пор пока все объекты не будут

включены в один кластер до достижения заданного «порога» сходства.

Мера сходства для объединения двух кластеров определяется двумя

методами:

Метод «ближайшего соседа» — степень сходства оценивается по

степени сходства между наиболее схожими (ближайшими) объектами этих

кластеров (рис. 1.1).

Пусть d

и d

— евклидовы расстояния, тогда, если d

, то S войдет в

кластер U по d

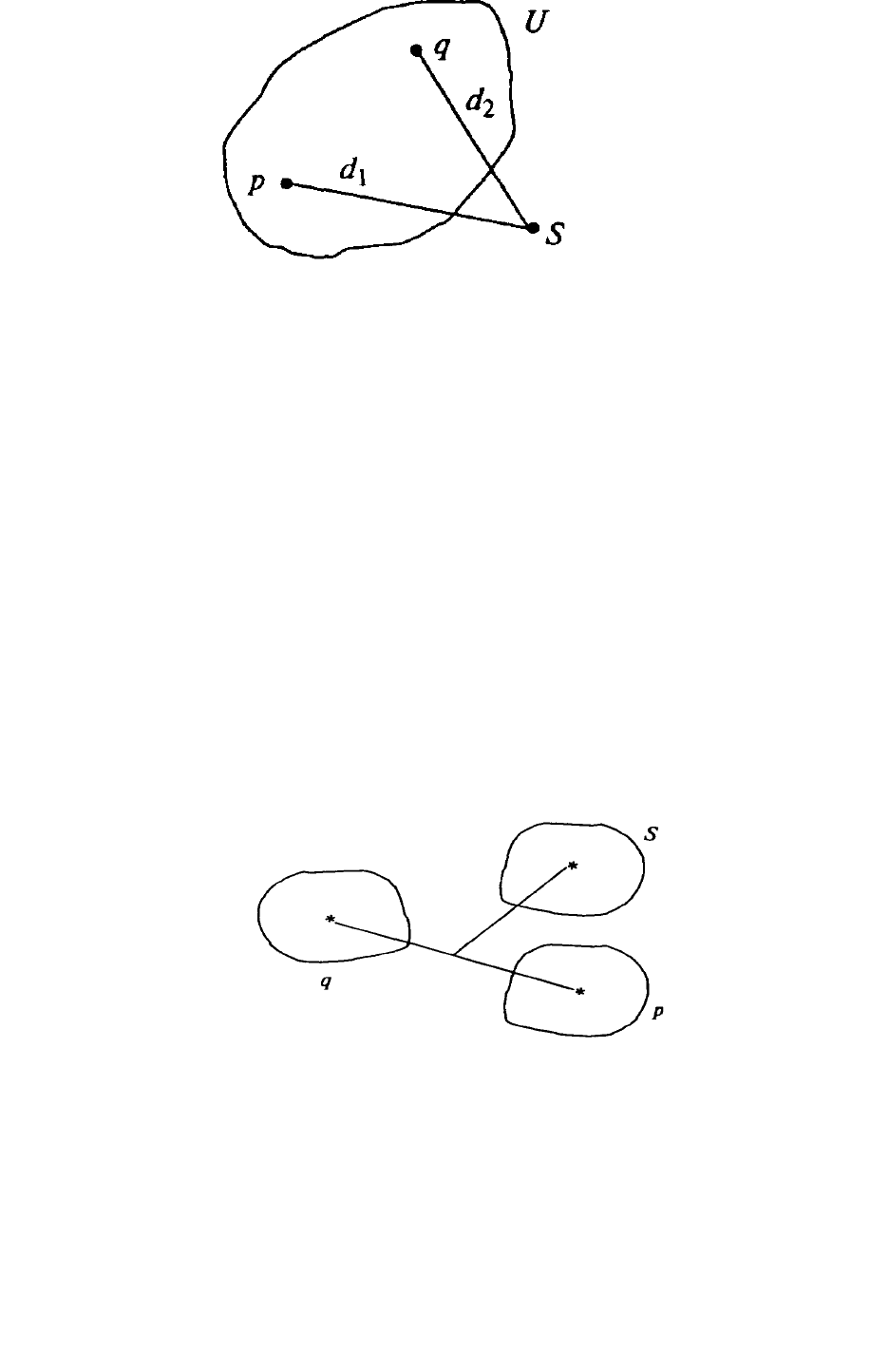
Метод «дальнего соседа» — степень сходства оценивается по степени

сходства между наиболее отдаленными (несхожими) объектами кластеров,

тогда S войдет в кластер U по d

Метод средней связи — степень сходства оценивается как средняя

величина степеней сходства между объектами кластеров. В этом случае S

войдет в кластер U по d=0,5(d

Метод медианной связи — расстояние между любым кластером S и

новым кластером, который получился в результате объединения кластеров р

и q, определяется как расстояние от центра кластера S до середины отрезка,

соединяющего центры кластеров р и q (рис.2.6).

Рис. 2.6. Определение расстояний между кластерами методом

медианной связи

Использование различных алгоритмов объединения в иерархических

агломеративных методах приводит к различным кластерным структурам и

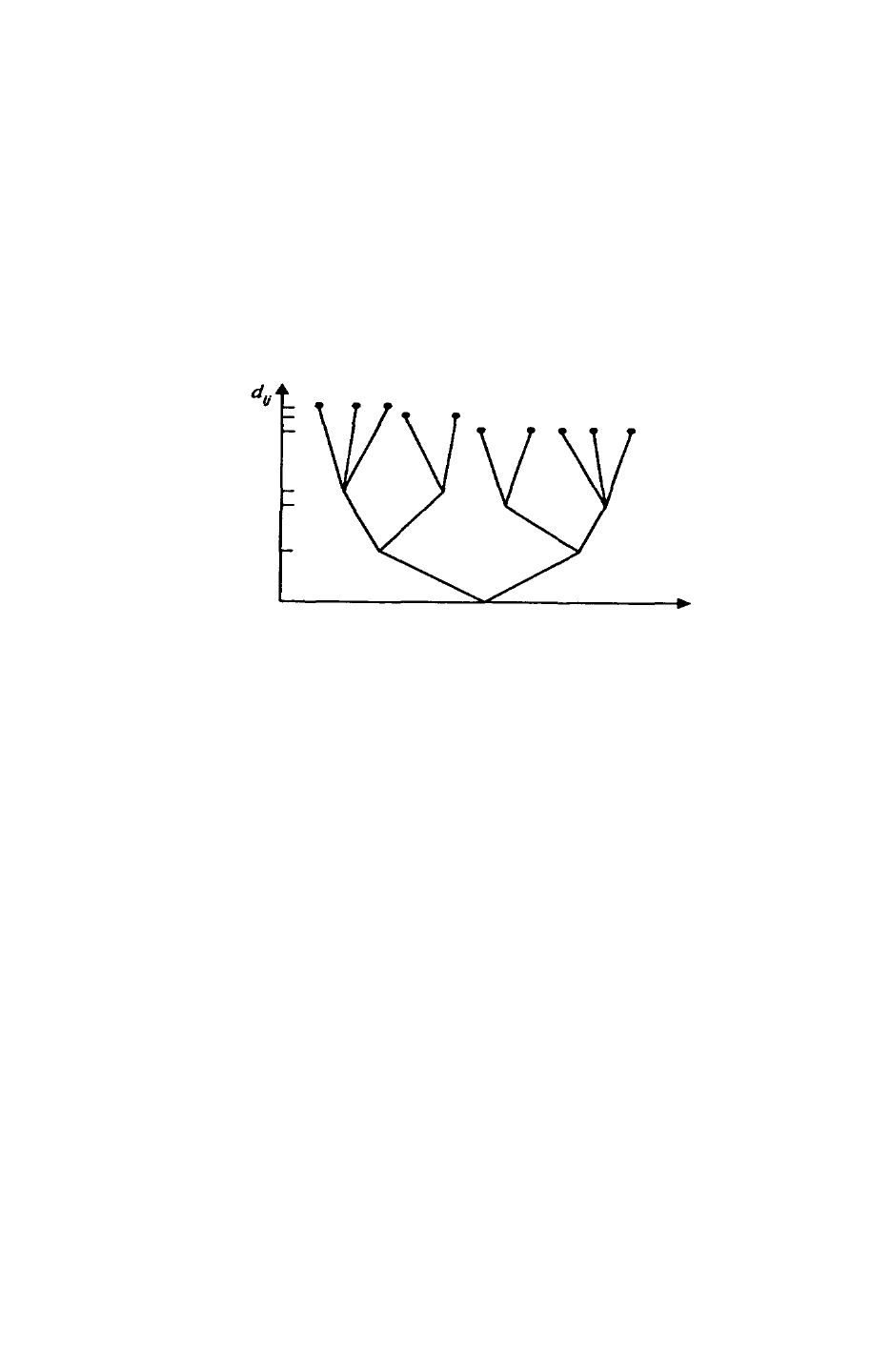
сильно влияет на качество проведения кластеризации. Поэтому алгоритм

должен выбираться с учетом имеющихся сведений о существующей

структуре совокупности наблюдаемых объектов или с учетом требований

оптимизации математических критериев.

Кроме рассмотренных агломеративных методов иерархического

кластерного анализа существуют методы, противоположные им по

логическому построению процедур классификации. Они называются

иерархические дивизимные методы. Основной исходной посылкой

дивизимных методов является то, что первоначально все объекты

принадлежат одному кластеру (классу). В процессе классификации по

определенным правилам постепенно от этого кластера отделяются группы

схожих между собой объектов.

Рис.2.5. Дендрограмма иерархического дивизимного алгоритма

Таким образом, на каждом шаге количество кластеров возрастает, а мера

расстояния между кластерами уменьшается. Дендрограмма для дивизимных

иерархических методов изображена на рис. 2.5.

Т4 4. Итеративные методы кластерного анализа

Наряду с иерархическими методами классификации существует

многочисленная группа так называемых итеративных методов кластерного

анализа. Сущность их заключается в том, что процесс классификации

начинается с задания некоторых начальных условий (количество образуемых

кластеров, порог завершения процесса классификации и т. д.). Итеративные

методы в большей степени, чем иерархические, требуют от пользователя

интуиции при выборе типа классификационных процедур и задания

начальных условий разбиения, так как большинство этих методов очень

чувствительны к изменению задаваемых параметров. Целесообразно сначала

провести классификацию по одному из иерархических методов или на

основании экспертных оценок, а затем уже подбирать начальное разбиение и

статистический критерий для работы итерационного алгоритма. Как и в

иерархическом кластерном анализе, в итерационных методах существует

проблема определения числа кластеров. В общем случае их число может

быть неизвестно. Не все итеративные методы требуют первоначального

задания числа кластеров. Но для окончательного решения вопроса о

структуре изучаемой совокупности можно испробовать несколько

алгоритмов, меняя либо число образуемых кластеров, либо установленный

порог близости для объединения объектов в кластеры. Тогда появляется

возможность выбрать наилучшее разбиение по задаваемому критерию

качества.

Метод k-средних принадлежит к группе итеративных методов

эталонного типа. Само название метода было предложено Дж. Мак-Куином в

1967 г.

В отличие от иерархических процедур метод k-средних не требует

вычисления и хранения матрицы расстояний или сходств между объектами.

Алгоритм этого метода предполагает использование только исходных

значений переменных.

Пусть имеется п наблюдений, каждое из которых характеризуется р

признаками Х1, Х2,..., Х

. Эти наблюдения необходимо разбить на k

кластеров.

Шаг 1. Из п точек исследуемой совокупности отбираются случайным

образом или задаются исследователем исходя из каких-либо априорных

соображений k точек (объектов). Эти точки принимаются за эталоны.

Шаг 2. Каждому эталону присваивается порядковый номер, который

одновременно является и номером кластера.

Шаг 3. Из оставшихся (n-k) объектов извлекается точка Xi с

координатами (xi2,…,xip) и проверяется, к какому из эталонов (центров) она

находится ближе всего. Для этого используется одна из метрик, например,

евклидово расстояние:







)(

Шаг 4. Проверяемый объект присоединяется к тому центру (эталону),

которому соответствует dil (l=1,…,k)

Шаг 5. Эталон заменяется новым, пересчитанным с учетом

присоединенной точки, и вес его (количество объектов, входящих в данный

кластер) увеличивается на единицу. Если встречаются два или более

минимальных расстояния, то i-и объект присоединяют к центру с

наименьшим порядковым номером.

Шаг 6. Выбираем точку Xi+1 и для нее повторяются все процедуры.

Таким образом, через (n-k) шагов все точки (объекты) совокупности

окажутся отнесенными к одному из k кластеров, но на этом процесс

разбиения не заканчивается. Для того чтобы добиться устойчивости

разбиения по тому же правилу, все точки Х1, Х2,..., Х

опять подсоединяются

к полученным кластерам, при этом веса продолжают накапливаться. Новое

разбиение сравнивается с предыдущим. Если они совпадают, то работа

алгоритма завершается. В противном случае цикл повторяется.

Окончательное разбиение имеет центры тяжести, которые не совпадают с

эталонами, их можно обозначить С1, С2,..., С

. При этом каждая точка Xi,( i =

1, 2, ..., n) будет относиться к такому кластеру (классу) l, для которого

D(xj,cl)=min d(xj,cj)

Возможны два варианта модификации метода k-средних: