Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.


411
Приклад 3. Дослідити збіжність ряду
...
)1nln(
1
...
4ln
1
3ln
1
2ln
1
+
+
++++
Розв
’язування. Знаходимо
.
)2nln(
)1nln(
lim
)1nln(
1
:
)2nln(
1
liml
nn
+
+
=
+
+
==
∞→∞→
Одержану невизначеність типу
∞
∞
розкриємо за правилом
Лопіталя:
[]
[]
.1
n
1
1
n
2
1
lim
1n
2n
lim
2n
1
1n
1
lim
)2nln(
)1nln(
lim
nnnn
=
+
+
=
+
+
=
+
+
=
′
+
′
+
∞→∞→∞→∞→
Тому за ознакою Даламбера збіжність вихідного ряду встано-
вити неможливо. Якщо ознака Даламбера не дає відповіді на питан-
ня про збіжність ряду (при
l=1), потрібно використати інші ознаки
дослідження збіжності даного ряду.
4.3. Інтегральна ознака Коші
ТЕОРЕМА. Нехай y=f(x) - неперервна, монотонно спадна і
додатна в інтервалі [1,∞) функція, значення якої f(1),f(2), f(3) ,
…,f(n),…
співпадають з відповідними додатними членами ряду
u
1
+u
2
+u
3
+…+u
n
+… (8.15)
Тоді
для збіжності ряду необхідно і достатньо, щоб невласний
інтеграл
∫
∞
1
dx)x(f мав скінчену величину.
Доведення
. Розглянемо криволінійну трапецію , обмежену
лінією
y=f(x), з основою від x=1 до x=n, де n- довільне ціле додатне
число (мал. 1)
Площа фігури, обмежена даними лініями обчислюється за
формулою
∫
=
n
1
n
dx)x(fI (8.16)
Позначимо цілі точки основи
.nx,1nx,...,2x,1x =−===
Розглянемо дві ступінчаті фігури: одна з них (внутрішня) має пло-
щу, яка дорівнює
1n
uS)n(f....)3(f)2(f −=+++
, а друга
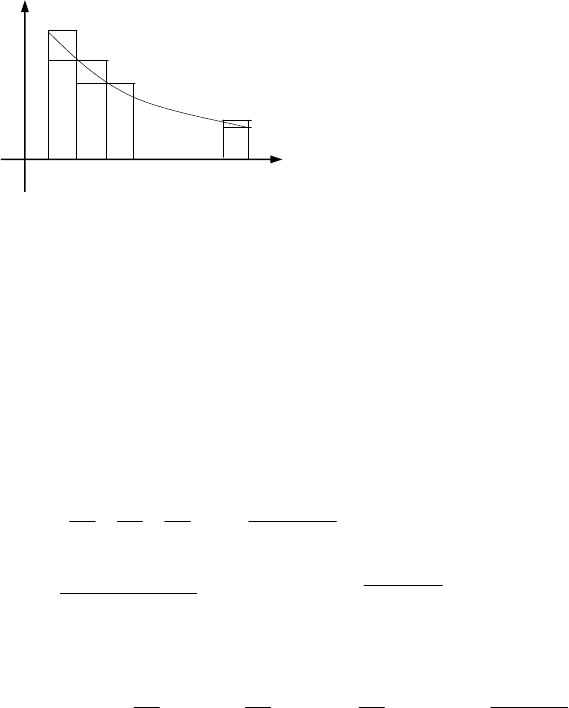
412
(зовнішня) - площу, що дорівнює
nn
uS)1n(f...)2(f)1(f −=−+++
, де .u...uuS
n21n
+++=
Площа першої фігури менша за площу криволінійної трапеції,
а площа другої більша за неї. Отже, маємо:
nnn1n
uSIuS −<<−
. (8.17)
Звідси одержимо дві нерівності :
1nn
uIS +<
, (8.18)
nnn
uIS +> . (8.19)
Оскільки функція
)x(f
додатна, то
інтеграл
n
I зростає разом з
n
.
Можливі два випадки:
1)Невласний інтеграл збігається, тобто
n
n
IlimI
∞→
=
існує. Тоді
II
n
< і з нерівності (8.18) при довільному
n
знаходимо
.IuS
1n
+≤ Оскільки, частинні суми
n
S , обмежені і зростають з
ростом
n
, то згідно з відомою теоремою аналізу, існує границя
IuSSlim
1n
n
+<=
∞→
, тобто ряд збіжний.
2)Інтеграл розбігається. Тоді
∞→
n
I
, при ∞→
n
і із
нерівності (8.19) випливає, що
n
S
також необмежено зростає, а це
означає, що ряд розбігається.
Приклад
1. Дослідити збіжність ряду
...
)1n(
n
...
4
3
3
2
2
1
3333
+
+
++++
.
Розв
’язування. Функція
3
)1x(
x
)x(f
+
=
( вигляд її
встановлюємо із загального члена заміною
n
на
x
) набуває лише
додатних значень, монотонно спадає на інтервалі
[
)
∞,1 . Значення
3
2
1
)1(f =
, ,
3
2
)2(f
3
=
33
)1n(
n
)n(f,...,
4
3
)3(f
+
==
співпадають з членами заданого ряду. Отже функція
)x(f
задовольняє умовам ознаки Коші.
Питання про збіжність даного ряду зводиться до питання про
0 1 2 3 4 n-1 n
y=f(x)
y
x
Мал.1
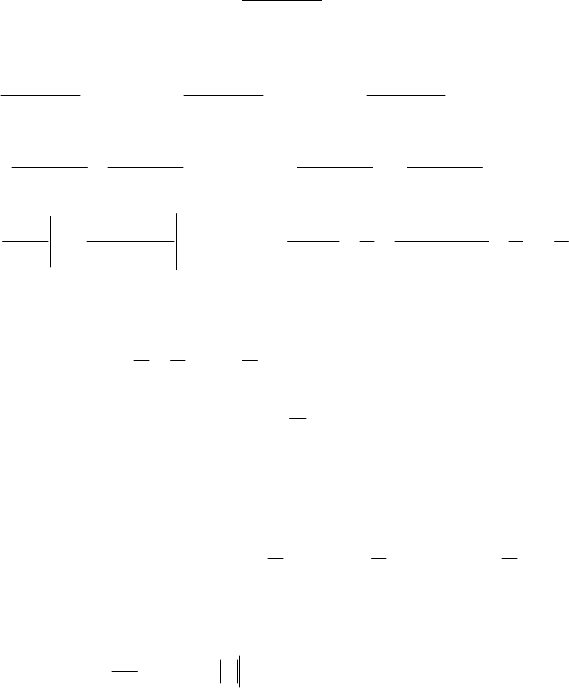
413
збіжність невласного інтеграла .dx
)1x(
x
1
3
∫
∞
+
Обчислимо даний інтеграл:
=
+
=
+
∫∫
∞→
∞
dx
)1x(
x
limdx
)1x(
x
N
1
3
N
1
3
=
+
−+
∫
∞→
dx
)1x(
11x
lim
N
1
3
N
.
8
3
8
1
)1N(2
1
2
1
1N
1
lim
)1x(2
1
1x
1
lim
)1x(
dx
)1x(
dx
limdx
)1x(
1
)1x(
1
lim
2
N
N
1
2
N
1
N
N
1
3
N
1
2
N
N
1
32
N
=
⎥
⎦
⎤
⎢
⎣
⎡
−
+
++
+
−=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
+
+
−=
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
=
∞→∞→
∞→∞→
∫∫∫
Невласний інтеграл збігається, а тому збігається і вихідний ряд.
Приклад
2. Дослідити збіжність гармонічного ряду
...
n
1
...
3
1
2
1
1 +++++ .
Розв
’язування. Функція
x
1
)x(f =
задовольняє умовам ознаки
Коші:
а) набуває додатних значень і монотонно спадає на інтервалі
[
)
∞,1 ;
б) значення
,1)1(f = ,
2
1
)2(f = ,
3
1
)3(f =
…, ...
n
1
)n(f =
співпадають з відповідними членами гармонічного ряду.
Обчислюємо невласний інтеграл
.)1lnN(lnlimxlnlim
x
dx
N
N
1
N
1
∞=−==
∞→∞→
∞
∫
Даний
невласний інтеграл розбігається, отже гармонічний
ряд теж розбігається.
§5. Знакопереміжні ряди. Ознака збіжності Лейбніца
Згадані ознаки збіжності числових рядів відносились до рядів
з додатними членами. Розглянемо тепер ряди, частина членів яких
додатна, а частина – від’ємна або рівна нулю.
Якщо члени числового ряду мають різні знаки, то ряд
називається знакозмінним.
414
Якщо два підряд члени ряду мають різні знаки, то знакозмін-
ний ряд називають знакопереміжним. Він має вигляд
...u)1(...uuuu
n
1n
4321
+−++−+−
−
Числа
u
1
, u
2
, u
3
,…,u
n
,… - додатні. На питання про збіжність
або розбіжність такого ряду дає відповідь ознака Лейбніца, яка фор-
мулюється у вигляді теореми.
ТЕОРЕМА
. Якщо із зростанням номера n члени ряду
...u)1(...uuuu
n
1n
4321
+−++−+−
−
(8.20)
за
абсолютною величиною спадають, а загальний член u
n
прямує до нуля при n
→
∞, тобто
n
n
ulim
∞→
=0,то ряд (8.20) збігається.
Доведення. Просумуємо парне число членів ряду (8.20):
.uu...uuuuS
n21n24321n2
−++−+−=
−
Тоді
).uu(SS
2
n21n2n2
2
n2
+
+
+
−+=
Оскільки за умовою теореми
2
n21n2
uu
+
+
≥ , то
n2
2
n2
SS ≥
+
,
тобто із зростанням
n суми з парними індексами також зростають.
Запишемо тепер часткову суму
n2
S в іншому вигляді:
.u)uu(...)uu()uu(uS
n2`1n22n254321n2
−−−−−−−−=
−−
Оскільки згідно з умовою теореми
1nn
uu
+
≥
при будь-якому
n
, то із останньої рівності випливає, що .uS
1n2
≤
Таким чином, послідовність
,...)2,1n(S
n2
= зростає із зро-
станням
n, і залишається обмеженою, а тому прямує до визначеної
границі, тобто
1n2
n
uSSlim ≤=
∞→
.
Тепер просумуємо непарне число членів ряду (8.20)
1n2n21n2n21n243211n2
uSuuu...uuuuS
++−+
+=+−++−+−=
.
Але тому що за умовою теореми
0ulim
1n2
n
=
+
∞→
то
.SSlimulimSlim)uS(limSlim
n2
n
1n2
n
n2
n
1n2n2
n
1n2
n
==+=+=
∞→
+
∞→∞→
+
∞→
+
∞→
Таким чином, доведено, що при даних умовах, ряд (8.20)
збігається і
1
uS0 ≤≤
.
Наслідок
. Якщо ряд (8.20) збігається, то залишок ряду також
представляє собою збіжний ряд і його сума дорівнює
nn
SSR −=
.
Залишок ряду, який задовольняє умовам тільки що доведеної
теореми, рівний
...u)1(u)1(R
2n
1n
1n
n
n
+−+−=
+
+
+
415
Звідси ...uuuR)1(
3n2n1nn
n
++−=−
+++
і ряд в правій частині
задовольняє умовам теореми. Тому
1nn
n
uR)1(0
+
≤−≤ , тобто
1nn
uR
+
≤ .
Ця формула дає оцінку величини похибки в тому випадку,
якщо замість суми ряду (8.20) береться сума
n
перших його членів.
Як видно, що для знакозмінних рядів із спадними членами ця по-
хибка не перевищує абсолютної величини першого із відкинутих
членів.
Приклад
1. Дослідити збіжність ряду
...
n
)1(
...
4
1
3
1
2
1
1
1n
+
−
++−+−
−
.
Розв
’язування. Абсолютні величини членів знакопереміжного
ряду спадають:
...
3
1
2
1
1 >>>
і границя загального члена рівна
нулю, тобто
.0
n
1
limulim
n
n
n
==
∞→∞→
Обидві умови ознаки Лейбніца виконуються, тому заданий
ряд збігається.
Якщо хоч одна із умов ознаки Лейбніца не виконується, то
знакопереміжний ряд буде розбіжним.
Приклад
2. Дослідити збіжність ряду
...
n
1n
)1(...
4
5
3
4
2
3
1
2
1n
+
+
−++−+−
−
.
Розв
’язування. Оскільки
,01)
n
1
1(lim
n
1n
limulim
nn
n
n
≠=+=
+
=
∞→∞→∞→
то даний ряд розбіжний.
Тут не виконується одна з умов ознаки Лейбніца збіжності
знакопереміжного ряду:
.0ulim
n
n
=
∞→
§ 6.
Абсолютна та умовна збіжність ряду
Розглянемо знакозмінний ряд, у якому члени з додатними і
від’ємними знаками не обов’язково чергуються. Позначимо такий
ряд
...u...uuuu
n4321
++++++
, де
)n,...,3,2,1i(u
i
=
- числа як
додатні, так і від’ємні.
416
Складаємо ряд з абсолютних величин його членів:
...u...uuu
n321
+++++ .
Якщо ряд з абсолютних величин збігається, то знакозмінний
ряд називається абсолютно збіжним. Якщо знакозмінний ряд збіга-
ється, а ряд, складений з абсолютних величин, розбігається, то зна-
козмінний ряд називається неабсолютно збіжним (або умовно збіж-
ним).
ТЕОРЕМА
. Якщо ряд, складений із абсолютних величин
членів даного ряду, збігається, то збігається і даний ряд.
Доведення. Позначимо через
n
S
суму
n
перших членів ряду
...u...uuu
n321
+++++ (8.21)
через
+
n
S - суму всіх додатних членів, а через
−
n
S - суму абсолютних
величин всіх від’ємних членів серед перших
n
членів ряду.
Тоді
−+
−=
nnn
SSS і =σ
n
−+
+
nn
SS , (8.22)
де
=σ
n
n321
u...uuu ++++ .
Оскільки згідно з умовою
n
σ має границю, тобто
σ=σ
∞→
n
n
lim
,
a
+
n
S
і
−
n
S
- додатні і зростаючі функції від
n
, причому
σ≤σ≤
+
nn
S
і
σ≤σ≤
−
nn
S
, то і вони мають границі. А отже і
−+
−=
nnn
SSS
при ∞→
n
прямує до границі, що і потрібно було до-
вести.
Це достатня ознака, але не є необхідною, тобто ряд
∑
∞
=1n
n
u мо-
же збігатися і тоді, коли ряд
∑
∞
=1n
n
u розбігається.
Приклад
1. Дослідити збіжність ряду
...
n
1
)1(...
4
1
3
1
2
1
1
1n
+−++−+−
−
.
Розв
’язування. Даний ряд називають рядом Лейбніца.
Оскільки
...,
n
1
...
4
1
3
1
2
1
1 >>>>>>
0
n
1
lim
n
=
∞→
, то даний ряд
збігається (згідно з ознакою Лейбніца). Ряд, складений із абсолют-
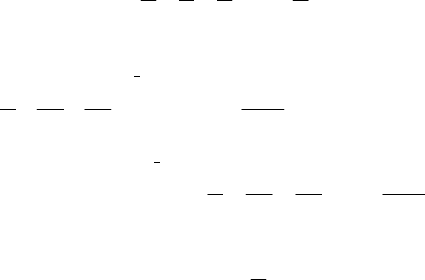
417
них величин ...,
n
1
...
4
1
3
1
2
1
1 ++++++
є гармонічним, який, як
відомо, розбіжний. Отже, даний ряд Лейбніца умовно збіжний.
Приклад
2. Дослідити збіжність ряду
...
2
1
)1(...
2
1
2
1
2
1
1
1n
1n
32
+−++−+−
−
−
.
Розв
’язування. Складемо ряд з абсолютних величин
...
2
1
...
2
1
2
1
2
1
1
1n32
++++++
−
Він збігається як ряд нескінченно спадної геометричної
прогресії із знаменником
.
2
1
q =
Отже заданий ряд збігається абсо-
лютно.
§ 7.
Поняття про степеневий ряд та його збіжність
Ряд, членами якого є функції змінної
x
, називається
функціональним.
Це ряд вигляду
...)x(f...)x(f)x(f)x(f
n321
+++++ (8.23)
Якщо
x
набуває будь-якого числового значення, то ряд (8.23)
стає числовим.
Сукупність всіх значень змінної
x
, при яких функціональний
ряд збігається, називається областю збіжності цього ряду. Будемо
розглядати ряди, областями збіжності яких служать різні інтервали
осі
Ox.
Якщо для всякого значення
x
із інтервалу
()
b,a
функціональний ряд збігається, то його сума є функція
...)x(f...)x(f)x(f)x(f)x(f
n321
+++++= (8.24)
Інакше кажучи, функція
)x(f
в інтервалі
()
b,a
розкладається в ряд.
Степеневим
рядом називається функціональний ряд виг-
ляду ...xa...xaxaa
n
n
2
210
+++++ , (8.25)
де
n210
a,...a,a,a - постійні числа.
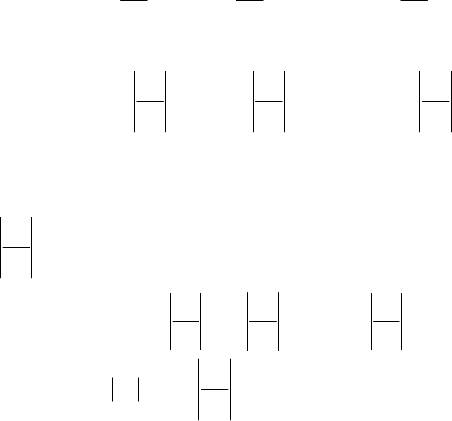
418
Іноді розглядають степеневий ряд більш загального вигляду:
...)ax(a...)ax(a)ax(aa
n
n
2
210
+−++−+−+ , (8.26)
де
a
- деяке постійне число. Останній ряд легко приводиться до по-
переднього степеневого ряду, якщо перепозначити
xax
′
=− .
Доведемо досить важливу теорему на якій буде базуватися
вивчення степеневих рядів.
ТЕОРЕМА
Абеля. Якщо степеневий ряд (8.25) збігається в
точці 0x
0
≠ , то він збігається абсолютно в інтервалі
()
|x|,|x|
00
−
, тобто при всякому
x
, що задовольняє умові
.|x||x|
0
<
Доведення. Із збіжності ряду (8.25) в точці
0
x випливає, що
його загальний член
0xa
n
0n
→
при
.
n
∞→ А тому всі члени цього
ряду є обмежені, тобто існує таке постійне додатне число
M
, що
для всякого
n
має місце нерівність
M|xa|
n
0n
<
. (8.27)
Запишемо ряд (8.25) так:
...
x
x
xa...
x
x
xa
x
x
xaa
n
0
n
0n
2
0
2
00
0
010
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
(8.28)
і складемо ряд із абсолютних величин членів цього ряду:
...
x
x
|xa|...
x
x
|xa|
x
x
|xa||a|
n
0
n
0n
2
0
2
02
0
010
++++⋅+
(8.29)
В силу установленої нерівності (8.27) кожний член ряду (8.29)
менший відповідного члена геометричної прогресії із знаменни-
ком
0
x
x
:
...
x
x
M...
x
x
M
x
x
MM
n
0
2
0
0
+++++ (8.30)
Якщо
0
x|x| < , то 1
x
x
0
< і ряд (8.30) збігається; а тому
збігається і ряд абсолютних величин (8.29), а значить, абсолютно
збігається сам ряд (8.25). Теорема доведена.
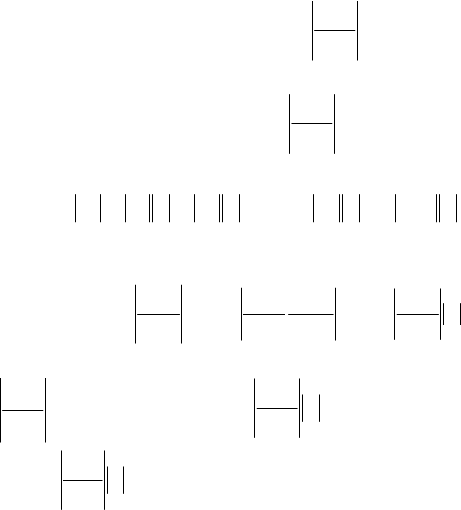
419
Наслідок. Якщо степеневий ряд (8.25) розбігається при
0
xx = , то він розбігається і при всякому
,
x
більшому за абсолют-
ною величиною, ніж
0
x
, тобто при
.x|x|
0
>
Таким чином можна стверджувати, що для будь-якого степе-
невого ряду, який має як точки збіжності так і точки розбіжності,
існує таке додатне число
R
, що для всіх
x
, по модулю менших
),R|x(|R <
ряд абсолютно збігається, а для всіх
x
, по модулю
більших
R|x(|R >
ряд розбігається. Число
R
називається радіусом
збіжності степеневого ряду (8.25). Інтервал
)R,R( −
називається
інтервалом збіжності. Якщо
,0R =
то інтервал збіжності
вироджується в точку, а при
∞=
R
- у всю числову вісь.
Для степеневих рядів (8.26) все сказане вище залишається в
силі, лише з тією різницею, що тепер центр інтервалу збіжності буде
лежати не в точці
0x =
, а в точці
0
xx =
. А отже, інтервалом
збіжності буде
).Rx,Rx(
00
+−
В наступній теоремі буде дано спосіб відшукання радіуса
збіжності степеневого ряду.
ТЕОРЕМА
. Якщо існує
1n
n
n
a
a
lim
+
∞→
, то радіус збіжності сте-
пеневого ряду знаходиться за формулою
.
a
a
limR
1n
n
n
+
→∞
=
(8.31)
Доведення
. Складемо ряд із абсолютних величин членів ряду
(8.25):
...xaxa...xaxaa
1n
1n
n
n
2
210
++++++
+
+
(8.32)
З попереднього параграфа відомо, що якщо збігається ряд
(8.32), то збігається ряд (8.25) абсолютно. Припустивши, що
∞→
n
,
одержимо
x
a
a
lim
x
x
a
a
lim
u
u
lim
n
1n
n
n
1n
n
1n
n
n
1n
n
+
∞→
+
+
∞→
+
∞→
==
.
Згідно з ознакою Даламбера, ряд (8.32) збігається, якщо
1
u
u
lim
n
1n
n
<
+
∞→
, тобто , якщо
1x
a
a
lim
n
1n
n
<
+
→∞
, і розбігається, якщо
.1x
a
a
lim
n
1n
n
>
+
→∞
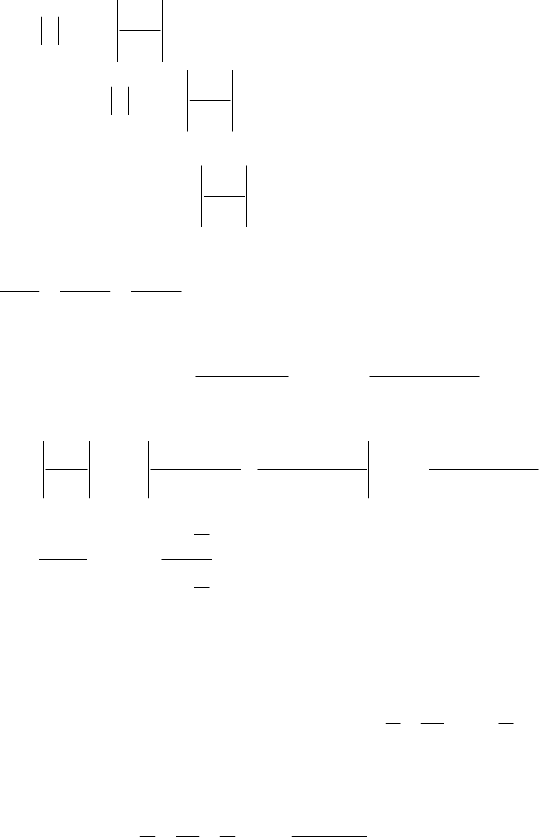
420
Отже, степеневий ряд (8.25) збігається, для всіх тих значень
x
, для яких
1n
n
n
a
a
limx
+
∞→
< , і розбігається для тих значень
x
, для
яких
1n
n
n
a
a
limx
+
→∞
>
.
Таким чином, для ряду (8.25), радіус збіжності знаходиться за
формулою .
a
a
limR
1n
n
n
+
→∞
=
Приклад
1. Знайти інтервал збіжності степеневого ряду
...
42
x
32
x
22
x
1
3
3
2
2
+
⋅
+
⋅
+
⋅
+
і дослідити його збіжність на кін-
цях інтервалу.
Розв
’язування. Тут
)1n(2
1
a
n
n
+
=
,
)2n(2
1
a
1n
1n
+
=
+
+
.
Знаходимо радіус збіжності ряду
.2
n
1
1
n
2
1
lim2
1n
2n
lim2
)1n(2
)2n(2
lim
)2n(2
1
:
)1n(2
1
lim
a
a
limR
nn
n
1n
n
1nn
n
1n
n
n
=
+
+
=
+
+
=
=
+
+
=
++
==
∞→∞→
+
∞→
+
∞→
+
∞→
Отже, ряд збігається в інтервалі
()
2,2−
. Щоб вирішити пи-
тання про збіжність степеневого ряду на кінцях інтервалу, покладе-
мо спочатку х
=2. Отримаємо гармонічний ряд
...,
n
1
...
3
1
2
1
1 +++++
який, як відомо, розбігається. При
2x −= одержимо знакозмінний
ряд Лейбніца:
...
n
)1(
...
4
1
3
1
2
1
1
1n
+
−
++−+−
−
.
Цей ряд збігається умовно. Таким чином, степеневий ряд
збігається для
[
)
2,2x −∈ .
