Шемякин Е.И., Смирнов Н.Н., Нигматулин Р.И., Натяганов В.Л. (редакторы) Газовая и волновая динамика
Подождите немного. Документ загружается.

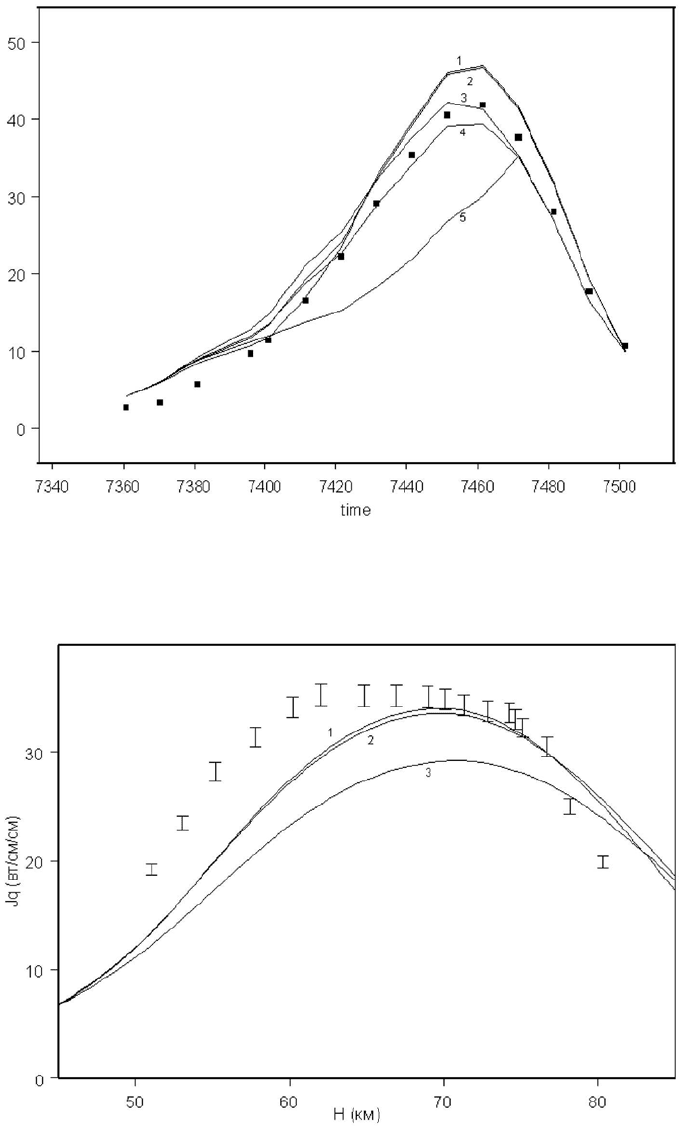
Рис. 1: Рассчитанные и измеренные тепловые потоки на траектории «OREX»
Рис. 2: Рассчитанные и измеренные тепловые потоки в точке торможения ап-
парата «Space Shuttle»
174
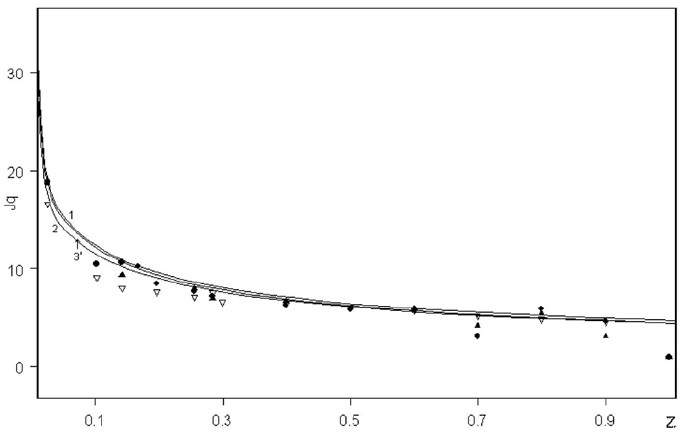
Рис. 3: Рассчитанные и измеренные тепловые потоки на боковой поверхности
«Space Shuttle»
образование NO на поверхности не учитывается. Использование в этой модели дру-
гих величин параметров вполне логично, так как рассматривается покрытие SiC, а
не RCG, для которого была первоначально построена эта модель.
На рис. 2 приведено сравнение данных по тепловым потокам, полученных во вре-
мя пятого полета корабля «Спейс Шаттл» в критической точке покрытой материалом
RCC носовой капсулы (вертикальные отрезки)[18] . Видно, что модели 1 (кривая 2)и
3’ (кривая 1) достаточно хорошо предсказывают уровень тепловых потоков в окрест-
ности критической точки этого аппарата при больших и средних высотах (включая
теплонапряженную точку траектории). Более низкие уровни тепловых потоков пред-
сказывает модель 2 (кривая 3). Отличие рассчитанных тепловых потоков от экспери-
ментальных, при высотах ниже 60 км наблюдается для всех моделей. Возможно оно
связано с выбором газодинамической модели течения при численном моделировании
или с трудностями измерения тепловых потоков в летных условиях.
На рис. 3 приведено сравнение рассчитанных тепловых потоков к боковой по-
верхности «Спейс Шаттл» в теплонапряженной точке траектории (высота полета
H 70.2 км) с экспериментально измеренными во время второго (светлые треуголь-
ники), третьего (точки) и пятого полетов (темные треугольники) [19]. Видно, что
модели катализа 1, 2 и 3’, разработанные для покрытий SiC и RCC, дают несколь-
ко завышенные величины тепловых потоков к боковой поверхности, так как на ней
используется покрытие RCG, свойства которого ближе к некаталитической поверх-
ности. При удалении от критической точки влияние образования NO на поверхности
не сказывается.
175
Заключение.
1. Исследована возможность предсказания с помощью имеющихся в литерату-
ре моделей гетерогенного катализа, учитывающим образование NO на поверхности,
уровня тепловых потоков на силиконизированных теплозащитных покрытиях при
входе в атмосферу Земли космических аппаратов «Спейс Шаттл» и «OREX». Пока-
зано, что эти модели еще не позволяют достаточно точно предсказать теплообмен в
широком диапазоне изменения условий в набегающем потоке.
2. Установлено, что определение параметров модели катализа с помощью под-
гонки под экспериментальные данные неоднозначно и существенно зависит от вы-
бранного механизма реакций на поверхности. В частности, одинаковые величины
тепловых потоков могут быть получены для различных наборов параметров моделей,
в том числе и для различных механизмов протекания гетерогенных каталитических
процессов.
Работа выполнена при поддержке Российского фонда фундаментальных исследо-
ваний (проект № 02–01–00759).
Литература
[1] Ковалев В. Л. Гетерогенные каталитические процессы в аэротермодинамике.
— М.: Физматлит, 2002.
[2] Goulard R. On catalytic recombination rates in hypersonic stagnation heat
transfer. — Jet Propuls, 1958, V. 28, № 11.
[3] Ковалев В. Л., Крупнов А. А. Особенности моделирования теплообмена с
каталитическими поверхностями при входе тел в атмосферу Земли. — Вест.
Моск. ун–та, Сер. 1, Мат. Мех., 1998, № 5.
[4] Bruno C., Guarino L. Re-entry problems. — In: Capitelli M, Beardsley J. M.,
ed. Nonequilibrium processes in ionized gases, NATO–ASI Series B, ESTEC,
ESA–SP–367, 1994.
[5] Copelend R. A. Pallix J. B., Stewart D. A. Surface-catalysed NO from
recombination of N and O atoms. — J. Thermoph. and Heat Transfer, 1998,
V.12,№4.
[6] Nasuti F., Barbato M., Bruno C. Material-dependent catalytic recombination
modeling for hypersonic flows. — J. Thermophysics and Heat Transfer, 1996,
V.10,№1.
[7] Kurotaki T. Construction of Catalytic Model on SiO
2
-Based Surface and
Application to Real Trajectory. — AIAA Paper 2000 – 2366.
[8] Ковалев В. Л., Суслов О. Н. Модель взаимодействия частично ионизованно-
го воздуха с каталитической поверхностью. В кн.: Исследования по гипер-
звуковой аэродинамике и теплообмену с учетом неравновесных химических
реакций. — М.: Изд-во Моск. ун-та, 1987.
176
[9] Ковалев В. Л., Суслов О. Н. Моделирование взаимодействия частично иони-
зованного воздуха с каталитической поверхностью высокотемпературной теп-
лоизоляции. — Изв. РАН: МЖГ, 1996, № 5.
[10] Kovalev V. L., Suslov O. N., Tirskiy G. A. Phemenologic theory for
heterogeneous recombination of partially dissosiated air on high temperature
surfaces. Proc. NATO Advanced Study Institute on Molecular Physics and
Hypersonic Flows, NATO–ASI Series C: Mathematical and Physical Sciencies,
V. 482. — Dordrecht, NL: Kluwer Acad Publ, 1996.
[11] Kolodziej P., Stewart D. A. Nitrogen recombination on high–temperature
reusable surface insulation and the analysis of its effects on surface catalysis.
— AIAA Paper 87–1637.
[12] Scott C. D. Catalytic recombination of nitrogen and oxygen on high temperature.
— AIAA Paper 80–1477.
[13] Агафонов В. П., Кузнецов М. М. Моделирование неравновесных тепловых
потоков к каталитической поверхности. — Ученые записки ЦАГИ,1979, Т.
10, № 4.
[14] Ковалев В. Л., Крупнов А. А. Численный метод решения уравнений многоком-
понентного турбулентного вязкого ударного слоя у каталитической поверхно-
сти. — Вестник Московского ун-та. Сер. Математика. Механика., N 3, 1994,
с. 66-74, Transfer, 1998, V. 12, № 4.
[15] Ковалев В. Л., Крупнов А. А., Тирский Г. А. Решение уравнений вязкого
ударного слоя методом простых глобальных итераций по градиенту давления
и форме ударной волны. — Докл. РАН, 1994, Т. 338, № 3.
[16] Gubta R. N., Moss J. N., Simmonds J. L. at al. Space Shuttle Heating Analysis
with Variation in Angle of Attack and Surface Condition. — AIAA Paper 83–
0486.
[17] High Enthalpy Flow Organized Session and Workshop. Proc. of 13th NAL Symp.
on Aircraft Computational Aerodynamics. — Japan, NAL SP–29, 1995.
[18] Curry D. M., Rochelle W. C., Chao D. C., Ting P. C. Space Shuttle Orbiter Nose
Cap Thermal Analysis. — AIAA Paper 86–0388.
[19] Scott C. D. Effect of nonequilibrium and wall catalysis on shuttle heat transfer.
— J. Spacecraft and Rockets, 1985, V. 22, № 5.
177

Вынужденные продольные колебания музыкальных
струн, обусловленные их поперечными колебаниями
Демьянов Ю. А., Малашин А. А.
Решения задач распространения поперечно-продольных волн в гибких деформиру-
емых нитях базируются на пионерской работе Х.Рахматулина [1] и его школы [2, 3]
и обстоятельно изложены в [4]. В частности, в работах [1, 4] выводится система
уравнений, описывающих процесс распространения поперечно-продольных волн при
поперечном ударе, а также условия в окрестности точки излома частей нити (усло-
вия на поперечной волне). В работе [1] указано, что «при ударе по струне вдоль
нее побежит волна продольного растяжения, которая в обычной теории колебания
струны во внимание не принимается».
В работе [5] на основе нелинейных уравнений распространения поперечно-
продольных волн, приведенных в [1, 4], получены линеаризированные уравнения
поперечно-продольных колебаний гибкой натянутой струны. Установлено, что хотя
поперечные смещения на порядок больше продольных, вклад поперечных и продоль-
ных деформаций в динамическое нагружение оказывается одного порядка. В рамках
линеаризированного подхода выведены соотношения для разрывов скоростей и де-
формаций продольных волн на поперечной волне.
В данной работе исследуются причины возникновения вынужденных продольных
колебаний, обусловленных поперечными колебаниями, возникающими в период воз-
действия на струну. Для пояснения сущности процесса анализ проводится для наи-
более простого случая «точечного удара» с постоянной скоростью на струну, жестко
закрепленную в точках заделки. При этом, как для нелинейного, так и для линей-
ного случаев будут существовать лишь области постоянных значений продольных и
поперечных составляющих скоростей
∂x
∂t
,
∂y
∂t
и деформаций
∂x
∂s
,
∂y
∂s
. Как будет видно
из дальнейшего, уравнения продольных колебаний при этом оказываются однород-
ными, и с первого взгляда не понятна причина появления вынужденных продольных
колебаний, которые, тем не менее, легко можно получить, если решать эту задачу
методом разделения переменных. В данной статье анализируется причина возник-
новения вынужденных продольных колебаний с использованием решений волновых
уравнений. Дело в том, что в этом случае на поперечных волнах всегда возника-
ют разрывы продольных составляющих скоростей и деформаций. В силу этого, как
показано ниже, имеет место суперпозиция двух процессов: а) распространения про-
дольных волн между точками крепления без какого-либо разрыва величин на попе-
речных волнах, б) распространения поперечных волн, несущих неизменный разрыв
продольных составляющих скоростей и деформаций вплоть до прихода этих волн в
места закрепления, что является определяющим для понимания проблемы, так как
фронт поперечных волн является источником возбуждения продольных колебаний.
Ниже представлены теоретические результаты, подтверждающие этот вывод. Указа-
ны более общие случаи воздействий, на которые также распространяется сделанный
вывод.
178
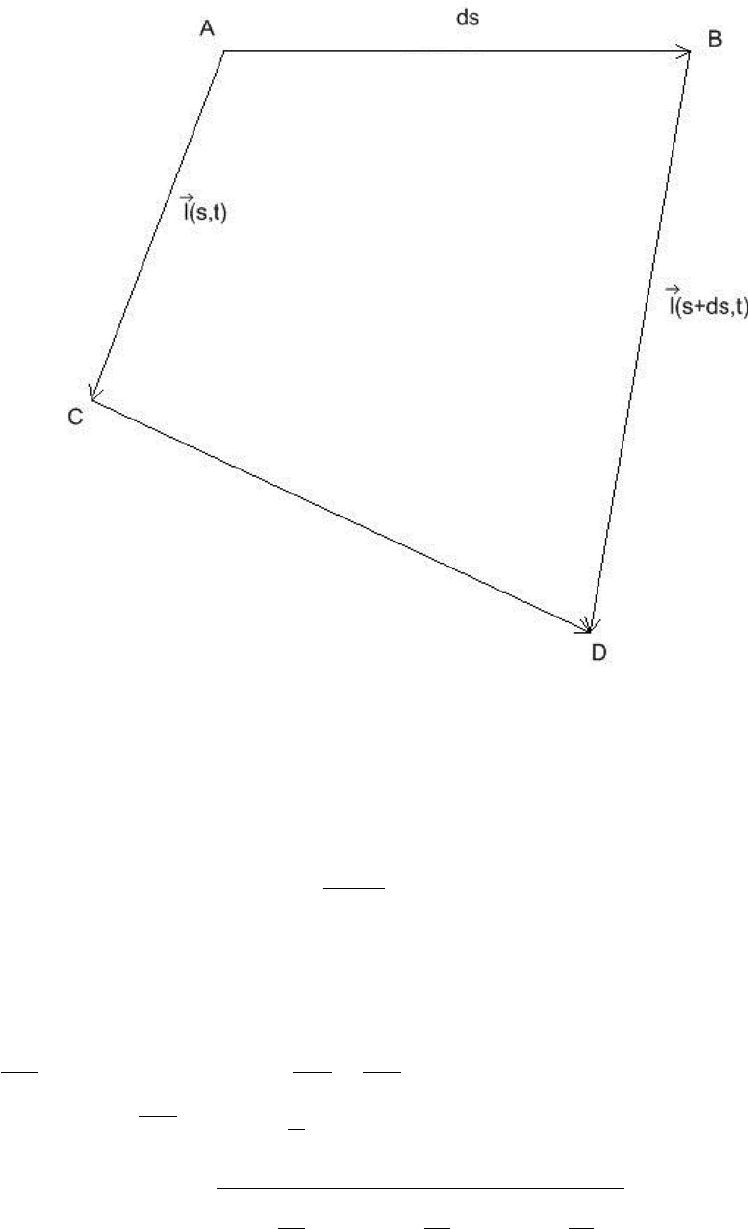
Рис. 1.
1.Вывод линеаризированных уравнений поперечно-продольных колебаний гибкой
натянутой струны начнем, следуя [5], с вывода уравнений сохранения массы и из-
менения количества движения элемента ∆s струны, где s — лагранжева координата
частиц струны, совпадающая с декартовой координатой x ненатянутой струны. Де-
формация элемента ∆s равна e =
CD−∆s
∆s
. Закон сохранения массы имеет вид:
ρ
0
∆s = ρ(1 + e)∆s, ρ
0
= ρ(1 + e)
где ρ
0
, ρ -начальная и текущая плотности струны. Из рис. 1
видно, что
AD =∆s ·
¯
i +
¯
l(s +∆s, t), CD = AD −
¯
l(s, t)=∆s ·
¯
i +[
¯
l(s +∆s, t) −
¯
l(s, t)]
при ∆s → 0,
CD =∆s(
¯
i +
∂
¯
l
∂s
),где
¯
l(s, t) -вектор смещения точки s.
Отсюда следует, что
e =
1+
∂x
∂s
2
+
1+
∂y
∂s
2
+
1+
∂z
∂s
2
− 1 (1)
179

где x(s, t), y(s, t), z(s, t) - проекции вектора
¯
l(s, t) на оси координат.
Если предположить, что в струне на элемент ∆s действуют лишь касательные
напряжения
¯
T (s +∆s, t),
¯
T (s, t), то из закона Ньютона следует, что
ρ
0
ds
∂
2
¯
l
∂t
2
=
¯
T (s +∆s, t) −
¯
T (s, t)=
∂
¯
T
∂s
ds, ρ
0
∂
2
¯
l
∂t
2
=
∂
¯
T
∂s
(2)
Проекции данного уравнения на оси координат имеют вид:
ρ
0
∂
2
x
∂t
2
=
∂
∂s
[T cos(
¯
i
¯
T )], cos(
¯
i
¯
T )=
1+
∂x
∂s
(1 + e)
−1
ρ
0
∂
2
y
∂t
2
=
∂
∂s
[T cos(
¯
j
¯
T )], cos(
¯
j
¯
T )=
1+
∂y
∂s
(1 + e)
−1
(3)
ρ
0
∂
2
z
∂t
2
=
∂
∂s
[T cos(
¯
k
¯
T )], cos(
¯
k
¯
T )=
1+
∂z
∂s
(1 + e)
−1
Для дальнейшего рассмотрения существенным оказывается то, что струна имеет
начальное натяжение T
0
= Ee
0
(E- модуль Юнга), и в данном случае продольное
смещение целесообразно представить в виде x = e
0
s +¯x. Тогда возмущение дефор-
мации ˆe = e − e
0
будет:
ˆe =
1+e
0
+
∂¯x
∂s
2
+
∂y
∂s
2
+
∂z
∂s
2
− 1 − e
0
(4)
Если учитывать, что ˆe<<1,аследовательно
∂¯x
∂s
,
∂ ¯y
∂s
,
∂¯z
∂s
малы, можно получить
линеаризированное выражение:
ˆe =
∂ˆx
∂s
+
1
2(1 + e
0
)
∂y
∂s
2
+
∂y
∂s
2
(4
)
Отсюда следует, что вклад как поперечных, так и продольных составляющих
деформации в динамическое нагружение оказывается одного порядка. несмотря на
то, что поперечные смещения на порядок больше продольных (они входят в (4’)
квадратами производных ).
Уравнения поперечных и продольных колебаний (2) в первом приближении с
учетом того, что в этом случае
T cos(
¯
j
¯
T ) ≈
Ee
0
1+e
0
∂y
∂s
,Tcos(
¯
k
¯
T ) ≈
Ee
0
1+e
0
∂z
∂s
,
T cos(
¯
i
¯
T )=Ee
0
+ E
∂¯x
∂s
+
1
2(1 + e
0
)
2
∂y
∂s
2
+
∂z
∂s
2
,
принимают следующий вид:
∂
2
y
∂t
2
= b
2
0
∂
2
y
∂s
2
,
∂
2
z
∂t
2
= b
2
0
∂
2
z
∂s
2
(5)
180
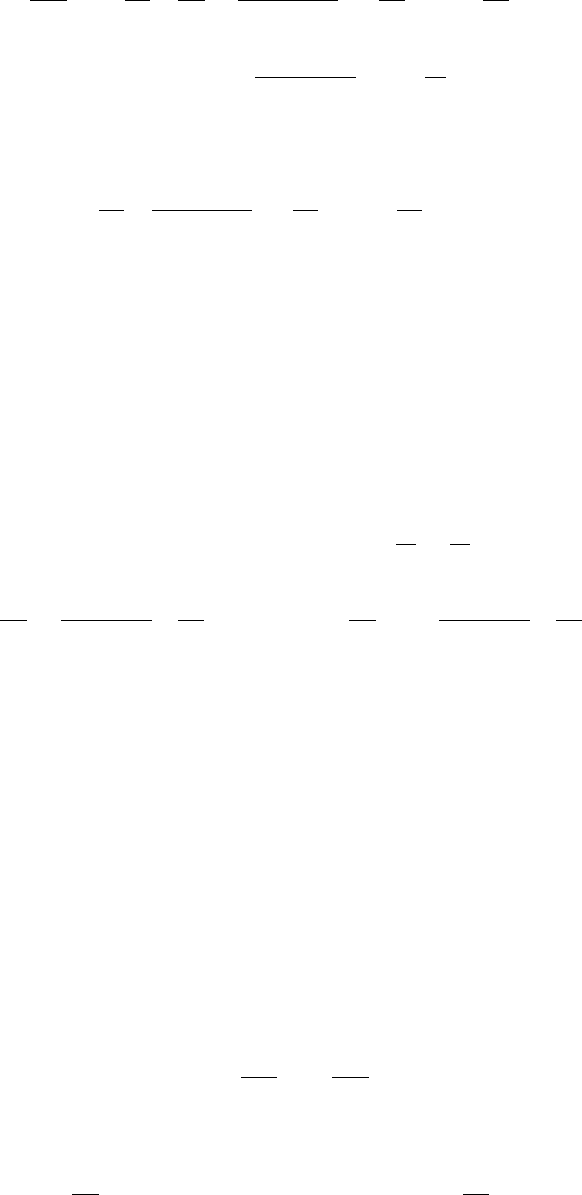
∂
2
¯x
∂t
2
= a
2
0
∂
∂s
∂¯x
∂s
+
1
2(1 + e
0
)
2
∂y
∂s
2
+
∂z
∂s
2
, (6)
где b
2
0
=
Ee
0
ρ
0
(1 + e
0
)
,a
2
0
=
E
ρ
0
Данные результаты можно получить [5], если воспользоваться методами теории воз-
мущений, приняв за малый параметр возмущение деформации ˆe = e−e
0
. Из-за нали-
чия неоднородности a
2
0
∂
∂s
1
2(1 + e
0
)
2
∂y
∂s
2
+
∂z
∂s
2
в уравнении (6) процесс
распространения продольных колебаний представляет собой суперпозицию собствен-
ных колебаний и вынужденных продольных колебаний на частотах поперечных.
Необходимо отметить, что постановка задач продольных колебаний принципи-
ально отличается от постановки задач поперечных колебаний тем, что скорости и
деформации продольных колебаний терпят разрывы на поперечных волнах. В самом
деле, исходя из соотношений на поперечной волне, полученных в работе [1]:
ρ
0
(b + u
1
)(V
1
cos β − u
1
)=T (cos γ − 1)(1 + e
1
) (7)
ρ
0
(b + u
1
)V
1
sin β = T sin γ(1 + e
1
) (8)
можно получить следующие соотношения [6] для
∂¯x
∂t
и
∂¯x
∂s
:
∂¯x
∂s
+
b
2
0
2(1 + e
0
)
∂y
∂s
2
=0,
∂¯x
∂t
=
b
2
0
2(1 + e
0
)
∂y
∂s
2
(9)
которые выражают, соответственно, в первом приближении непрерывность полной
деформации и применение закона количества движения в направлении оси Ox.Здесь
квадратные скобки выражают разрывы соответствующих параметров справа и слева
от поперечных волн.
2.Пусть на струну, жестко закрепленную в точках x =0, x = L, воздействует
вточкеx = c бесконечно тонкая палочка, имеющая проекции скорости V
0
и V
τ
в
направлениях соответственно нормальных к ее длине и вдоль длины (V
τ
-скорость
скольжения палочки по струне).
Для упрощения анализа примем, что V
0
= const, V
τ
= const. Направляя ось Ox
по длине палочки, Oy по направлению проекции скорости V
0
, будем иметь движе-
ние частиц струны в плоскости z =0, описывающееся для рассматриваемой задачи
уравнением поперечных колебаний:
∂
2
y
∂t
2
= b
2
0
∂
2
y
∂x
2
(10)
при следующих начальных и граничных условиях:
y(x, 0) =
∂y
∂x
(x, 0) = 0,y(0,t)=y(L, t)=0,
∂y
∂t
(x = c, t)=V
0
(11)
181
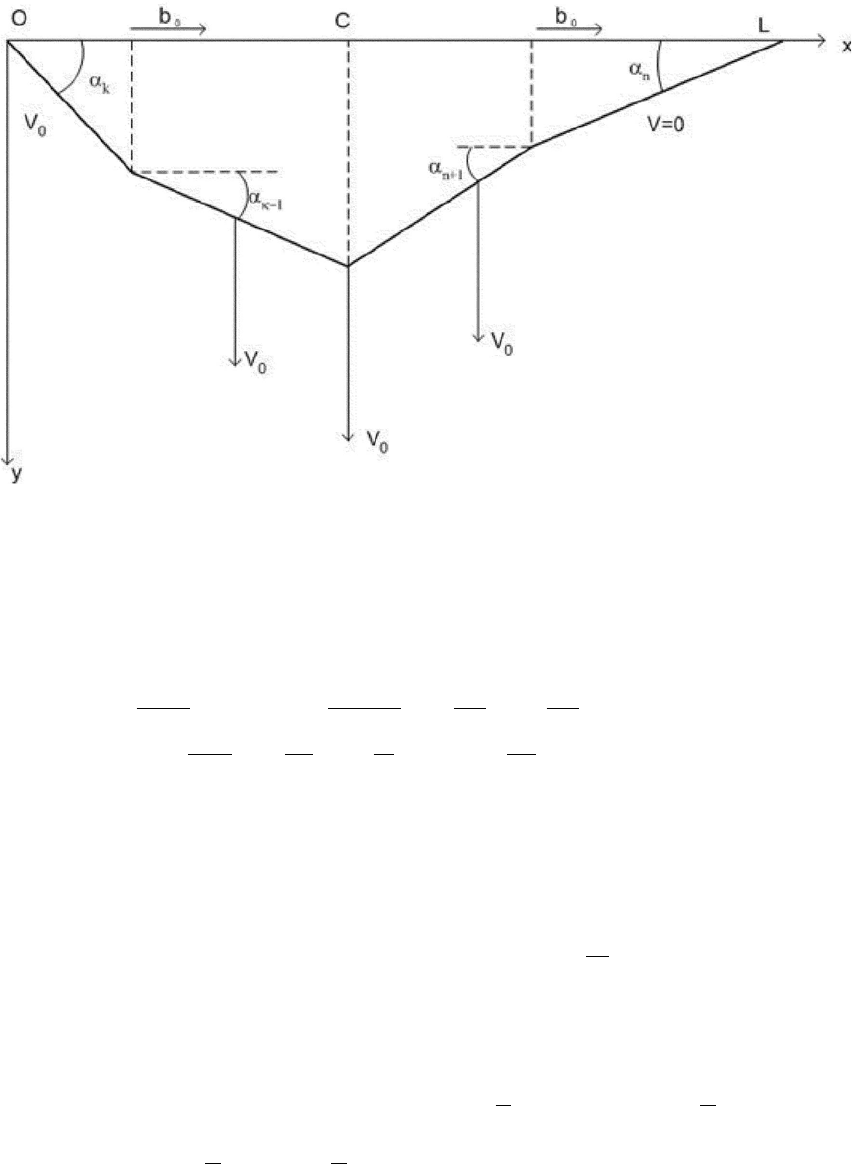
Рис. 2.
(b
0
- скорость распространения поперечных волн).
Решение этой задачи можно получить, если воспользоваться методом разделения
переменных:
y
0
(s, t)=
L−c−s
L−c
Vt−
∞
n=1
2V (L−C)
L−c
sin
bπn
L−c
t
sin
πn
L−c
(s − L + c); c ≤ s ≤ L
∞
n=1
2Vc
bπ
2
n
2
sin
bπn
c
t
sin
πn
c
(s − c)+
c−s
c
Vt; c ≤ s ≤ c.
(12)
Вместе с этим, данное решение может быть получено как методом распространя-
ющихся волн, так и методом характеристик и представляет собой волновой процесс,
схематично изображенный на рис. 2. Начальный угол α
0
наклона струны к оси X
определяется из условия:
tgα
0
=
¯
V
0
или α
0
≈
¯
V
0
, где
¯
V
0
=
V
0
b
0
<< 1.
После отражений поперечных волн от креплений x =0, x = L углы наклона
струны в этих точках равны 2α
0
. После достижения отраженной от крепления волной
точки x = c и отражения от нее, углы наклона струны в этих точках становятся
равными 3α
0
и т. д. Поэтому при времени 2k
c
b
0
<t<(2k +1)
c
b
0
углы наклона
струны соответственно в точках x =0,x = c суть θ
0
=2kα
0
, θ
1
=(2k +1)α
0
,
при времени (2k − 1)
c
b
0
<t<2k
c
b
0
соответствующие углы наклона суть θ
0
=2kα
0
,
θ
1
=(2k − 1)α
0
. Как показано выше, продольные смещения частиц струны x(s, t) в
первом приближении удовлетворяют уравнению (6), которое в нашем случае, когда
182
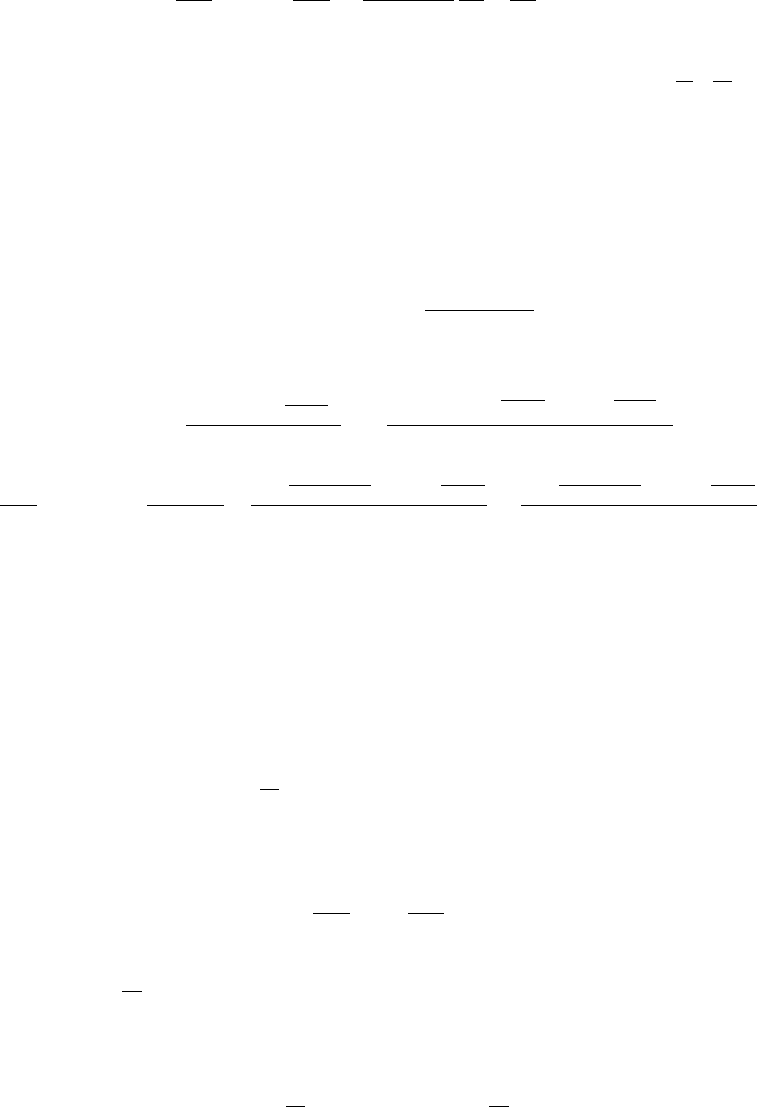
движение происходит в плоскости z =0, принимает вид:
∂
2
¯x
∂t
2
=¯a
2
0
∂
2
¯x
∂s
2
+
1
2(1 + e
0
)
∂
∂s
∂y
∂s
2
(13)
¯a
0
= a
0
(1 − e
0
)
−1
, a
0
- скорость продольных волн, выражение для
∂
∂s
∂y
∂s
2
может
быть найдено из (12). Решение данного уравнения может быть найдено методом
разделения переменных с учетом следующих граничных и начальных условий:
x(s, 0) = x
t
(s, 0) = 0 x(0,t)=x(c, t)=x(L, t)=0
и имеет следующий вид:
X(s, t)=
T
n
sin
πn(s − L
i
)
L
i
(14)
где
T
n
(t)=−
4V
2
0
t sin
πnb
0
t
L
i
π
2
n
2
b
0
(a
2
0
− b
2
0
)
− 8
V
2
0
b
0
c
cos
πna
0
t
Li
− cos
πnb
0
t
L
i
π
2
n
2
b
0
(a
2
0
− b
2
0
)
2
−
L
i
n
4
π
k + m = n
|k − m| = n
4V
0
π
2
b
2
0
km
cos
π(k+m)b
0
t
L
i
− cos
πna
0
t
L
i
n
2
a
2
0
−
(
k
+
m
)
2
b
2
−
cos
π(k−m)b
0
t
L
i
− cos
πna
0
t
L
i
n
2
a
2
0
−
(
k
−
m
)
2
b
2
0
где L
i
=
c, 0 <s<c
L − c, c<s<L
Анализируя полученное решение можно заметить, что в спектре продольных ко-
лебаний наряду с собственными частотами присутствует спектр вынужденных про-
дольных колебаний на частотах поперечных.
Наряду с этим волновое решение дает наиболее простое объяснение возникнове-
нию продольных колебаний на частотах поперечных.
В рассматриваемом случае
∂y
∂s
= const в каждой из приведенных на рис. 2 обла-
стей. Поэтому уравнение (13) в этих областях становится однородным и принимает
традиционный вид уравнения продольных колебаний:
∂
2
¯x
∂t
2
= a
2
0
∂
2
¯x
∂s
2
(15)
При формулировке задачи для уравнения (15), как показано в [6], кроме началь-
ных условий ¯x =
∂¯x
∂t
=0и граничных условий в точках s =0и s = L необходимо
ставить условия (9) на поперечных волнах и в точке воздействия палочки. Для рас-
сматриваемой задачи величины разрывов оказываются постоянными, не зависящими
от времени. Поэтому, решениями уравнения (15) являются области постоянных зна-
чений составляющих скоростей
∂¯x
∂t
и деформаций
∂¯x
∂s
, испытывающих разрывы на
поперечных волнах в соответствии с соотношениями (9). Источником данных волн
183
