Шапкин А.С., Шапкин В.А. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями
Подождите немного. Документ загружается.

101
õ
1
= 0,
,3,0
2
−=x
3,0
3
=x
ÿâëÿþòñÿ êðèòè÷åñêèìè òî÷êàìè
2-ãî ðîäà, êîòîðûå äåëÿò âñþ ÷èñëîâóþ îñü íà èíòåðâàëû:
,)3,0;( −−∞
),0;3,0(−
),3,0;0(
.);3,0( ∞
Âûÿñíèì çíàê âòîðîé
ïðîèçâîäíîé â óêàçàííûõ èíòåðâàëàõ. Íà èíòåðâàëå
)3,0;( −∞
âîçüìåì, íàïðèìåð, òî÷êó õ = 1; y″(1) = 14 < 0, çíà÷èò, êðèâàÿ
â ýòîì èíòåðâàëå âûïóêëà.
Íà èíòåðâàëå (0,3; 0) ðàññìîòðèì òî÷êó
:
2
1
−=x
,0
2
1
2
1
6
2
1
20
2
1
3
>=
−−
−⋅=
−
′′
y
çíà÷èò, êðèâàÿ íà ýòîì èíòåðâàëå âîãíóòà, âòîðàÿ ïðîèçâîäíàÿ
ïðè ïåðåõîäå ÷åðåç
3,0
2
−=x
ìåíÿåò çíàê ñ íà +, ñëåäîâàòåëüíî,
çíà÷åíèå
3,0−=x
ÿâëÿåòñÿ àáñöèññîé òî÷êè ïåðåãèáà. Àíàëîãè÷-
íî îïðåäåëÿåì, ÷òî íà èíòåðâàëå
)3,0;0(
êðèâàÿ âûïóêëà, à íà
èíòåðâàëå
);3,0( ∞
âîãíóòà; çíà÷åíèÿ õ = 0 è
3,0=x
ÿâëÿþòñÿ
àáñöèññàìè òî÷åê ïåðåãèáà êðèâîé.
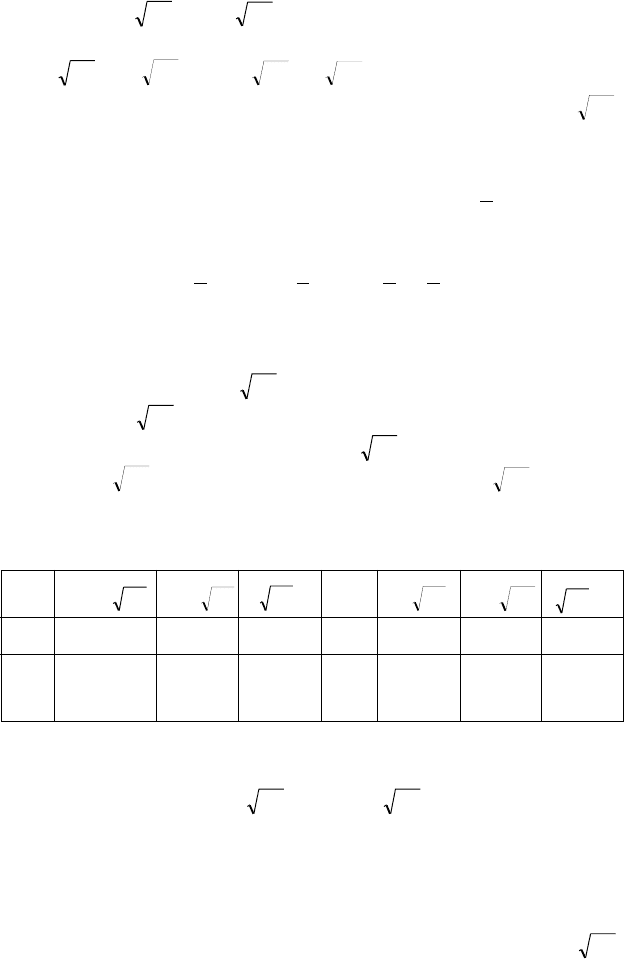
Ñîñòàâèì òàáëèöó èçìåíåíèÿ çíàêîâ y″(õ).
õ
)3,0;( −−∞
3,0−=x
)0;3,0(−
õ = 0
)3,0;0(
3,0
=x
);3,0( ∞
y″(õ) 0 + 0 0 +
y(õ)∩ ò.ï. ∪ ò.ï. ∩ ò.ï. ∪
ó ≈ 1,2 ó = 0 ó ≈ 1,2
Îïðåäåëèì çíà÷åíèÿ ôóíêöèè â òî÷êàõ ïåðåãèáà:
.22,1)3,0(;22,1)3,0(;0)0( −≈≈−= yyy
×òîáû òî÷íåå íàðèñîâàòü êðèâóþ ãðàôèêà, ìîæíî íàéòè
óãëû íàêëîíà êàñàòåëüíûõ, ïðîâåäåííûõ ê êðèâîé â òî÷êàõ
ïåðåãèáà. Òàê, ïðè õ = 0, ó′(0) = 2, ò.å. tg
α
= 2, ãäå
α
óãîë
íàêëîíà êàñàòåëüíîé ê êðèâîé â òî÷êå õ = 0, à ïðè
,3,0=x
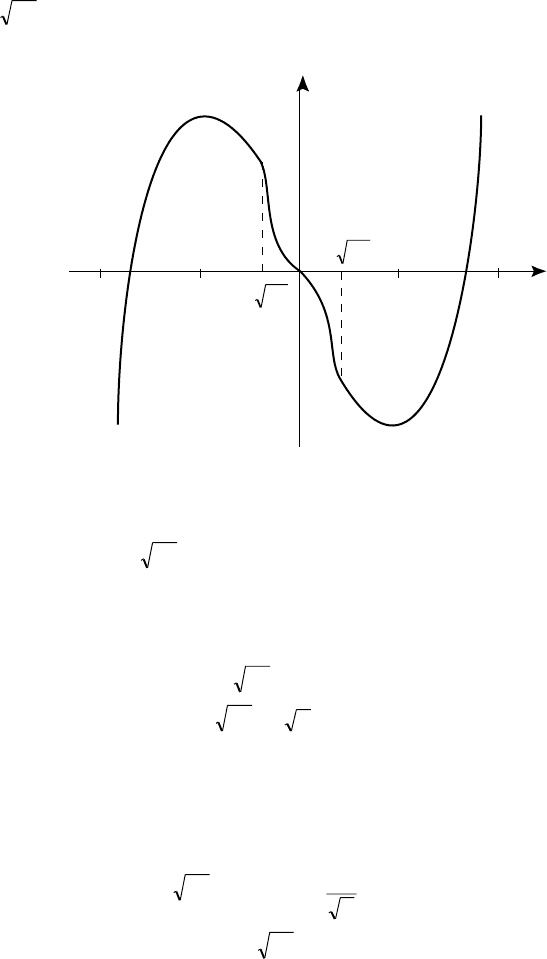
102
.45,2)3,0( −≈
′
y
Îêîí÷àòåëüíûé ãðàôèê ôóíêöèè y = õ
5
õ
3
2õ
èçîáðàæåí íà ðèñ. 24.
Ïðèìåð 2.31. Ïðîâåñòè ïîëíîå èññëåäîâàíèå è ïîñòðîèòü ãðà-
ôèê ôóíêöèè
.
3
2
xxy −=
1. Ôóíêöèÿ îïðåäåëåíà âñþäó íà èíòåðâàëå (∞; ∞).
2. Ôóíêöèÿ îáùåãî âèäà.
3. Íàéäåì òî÷êè ïåðåñå÷åíèÿ ñ îñÿìè êîîðäèíàò:
;0)1(
;0
3
3
2
3
2
=−
=−
xx
xx
õ
1
= 0; õ
2
= 1;
y(0) = 0; y(1) = 0.
Îïðåäåëèì çíà÷åíèÿ ôóíêöèè íà ãðàíèöàõ îáëàñòè ñóùåñòâî-
âàíèÿ:
.)(limlim
;)1(1
1
lim)(limlim
3
3
3
3
2
∞=∞+∞=−=
−∞=∞=
−=−=
−∞→−∞→
∞→∞→∞→
xxy
x
xxxy
xx
xxx
Ðèñ. 24
y
x
2 1
3,0
−
0
12
3,0
103
Âåðòèêàëüíûõ àñèìïòîò íåò, òàê êàê ôóíêöèÿ íå èìååò òî÷åê
ðàçðûâà. Îïðåäåëèì íàêëîííûå àñèìïòîòû:
.)(lim)(lim
;1
1
1
limlimlim
3
2
3
3
2
∞=+−=−=
−=
−
=
−
==
±∞→±∞→
±∞→±∞→±∞→
xxxkxyb
x
x
x
x
xx
x
y
k
xx
xxx
Òàê êàê b → ∞ ïðè õ → ∞, òî íàêëîííûõ àñèìïòîò êðèâàÿ íå
èìååò.
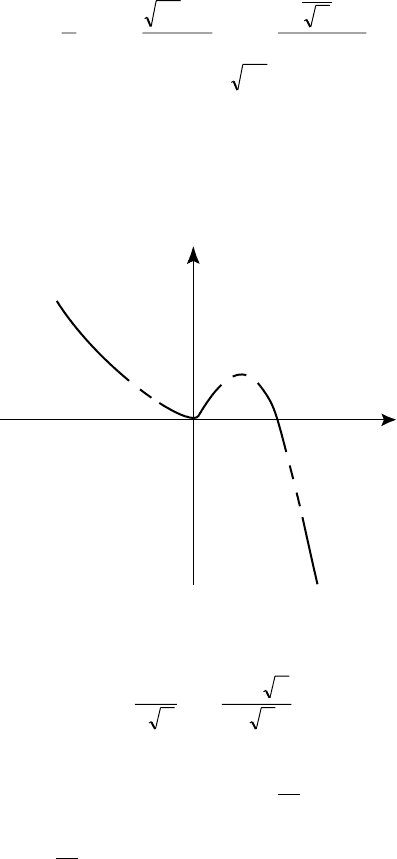
Íà ðèñ. 25 èçîáðàæåíà ïðîñòåéøàÿ êðèâàÿ, óäîâëåòâîðÿþùàÿ
ïðîâåäåííîìó èññëåäîâàíèþ.
4. Äàëåå ïðîäîëæèì èññëåäîâàíèå ïî ïåðâîé ïðîèçâîäíîé
;
3
32
1
3
2
3
3
3
x
x
x
y
−
=−=
′
ó′ = ∞ ïðè õ
1
= 0;
ó′ = 0 ïðè
;
27
8
2
=x
õ
1
= 0,
27
8
2
=x
êðèòè÷åñêèå òî÷êè.
Ðèñ. 25
0
y
x
1
104
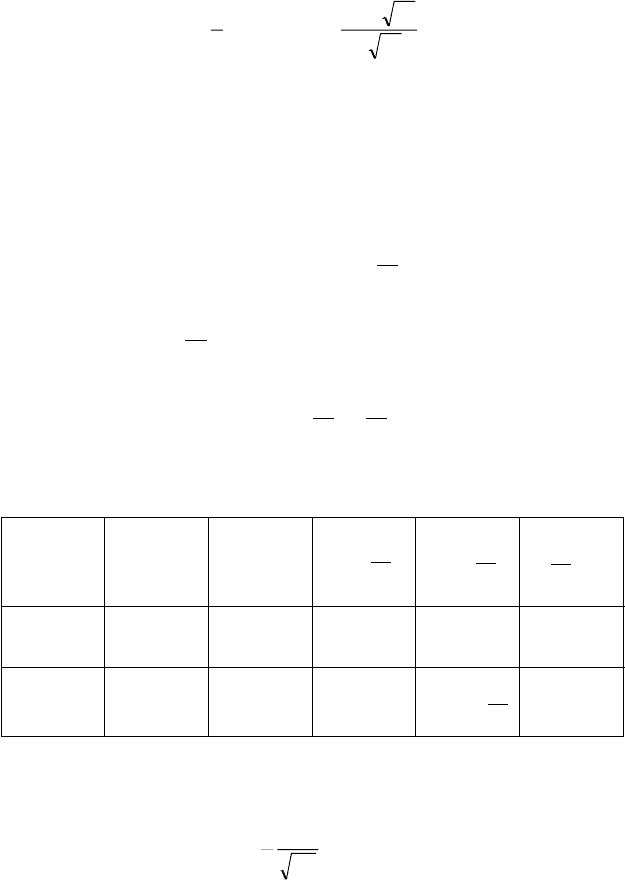
×òîáû âûÿñíèòü, ÿâëÿþòñÿ ëè îíè òî÷êàìè ýêñòðåìóìîâ, èñ-
ïîëüçóåì ïåðâîå äîñòàòî÷íîå óñëîâèå ýêñòðåìóìà
.04,0
1,03
1,032
)1,0(,0
3
5
)1(
3
3
>≈
−
=
′
<−=
′
yy
Ïðè ïðîõîæäåíèè ÷åðåç òî÷êó õ
1
= 0, ó′ ìåíÿåò çíàê ñ « »
íà «+»; çíà÷èò, òî÷êà õ = 0 ÿâëÿåòñÿ òî÷êîé ìèíèìóìà ôóíê-
öèè, ïðè÷åì ôóíêöèÿ èìååò â ýòîé òî÷êå òàê íàçûâàåìûé îñòðûé
ýñòðåìóì:
min = y(0) = 0.
Ïðè ïðîõîæäåíèè ÷åðåç òî÷êó
27
8
2
=x
ìû àíàëîãè÷íî ìîæåì
ïðîâåðèòü, ÷òî ïåðâàÿ ïðîèçâîäíàÿ ìåíÿåò çíàê ñ «+» íà «».
Çíà÷èò, òî÷êà
27
8
2
=x
ÿâëÿåòñÿ òî÷êîé ìàêñèìóìà:
.
27
4
27
8
max =
= y
Ñîñòàâèì òàáëèöó èçìåíåíèÿ çíàêîâ ïåðâîé ïðîèçâîäíîé.
x (∞; 0) x
1
= 0
27
8
;0
27
8
=x
∞
;
27
8
ó′(x) ∞ +0
y(x)
Tmin = 0 R
27
2
max =
T
5. Íàéäåì âòîðóþ ïðîèçâîäíóþ.
0
1
9
2
3
4
<−=
′′
x
y
âñåãäà.

105
Âòîðàÿ ïðîèçâîäíàÿ âñåãäà îòðèöàòåëüíà, çíà÷èò, òî÷åê ïåðå-
ãèáà íåò, êðèâàÿ âñåãäà âûïóêëà. Îêîí÷àòåëüíûé ãðàôèê ôóíê-
öèè
xxy −=
3
2
èçîáðàæåí íà ðèñ. 26.
Ïðèìåð 2.32. Ïðîâåñòè ïîëíîå èññëåäîâàíèå è ïîñòðîèòü ãðà-
ôèê ôóíêöèè
x
x
y
ln
=
.
Îáëàñòüþ îïðåäåëåíèÿ ôóíêöèè ÿâëÿþòñÿ èíòåðâàëû
(0; 1) ∪ (1; ∞).
Ôóíêöèÿ
x
x
y
ln
=
ÿâëÿåòñÿ ôóíêöèåé îáùåãî âèäà. Ïðè 0 < x < 1
y < 0, ïðè 1 < x < ∞ y > 0.
Âû÷èñëèì ïðåäåëüíûå çíà÷åíèÿ ôóíêöèè íà ãðàíèöàõ îáëàñ-
òè ñóùåñòâîâàíèÿ:
.
1
1
lim
ln
limlim
;
0
1
ln
limlim
;
0
1
ln
limlim
;0
0
ln
limlim
01
0101
0000
∞===
∞=
+
==
−∞=
−
==
=
∞−
==
∞→∞→∞→
+→
−→−→
+→+→
x
x
x
y
x
x
y
x
x
y
x
x
y
xxx
x
xx
xx
Ðèñ. 26
y
0 1
x
1 --
106
 ïîñëåäíåì ñëó÷àå ïðèìåíåíî ïðàâèëî Ëîïèòàëÿ.
Èç íàéäåííûõ ïðåäåëîâ ÿñíî, ÷òî ïðÿìàÿ õ = 1 ÿâëÿåòñÿ âåðòè-
êàëüíîé àñèìïòîòîé.
Îïðåäåëèì íàêëîííûå àñèìïòîòû:
.
1
1
lim
)(ln
)(
lim
ln
lim][lim
;0
ln
1
lim
ln
limlim
∞==
′
′
==−=
==
⋅
==
∞→∞→∞→∞→
∞→∞→∞→
x
x
x
x
x
kxyb
xxx
x
x
y
k
xxxx
xxx
Íàêëîííûõ àñèìïòîò ôóíêöèÿ íå èìååò, ãîðèçîíòàëüíûõ àñèìï-
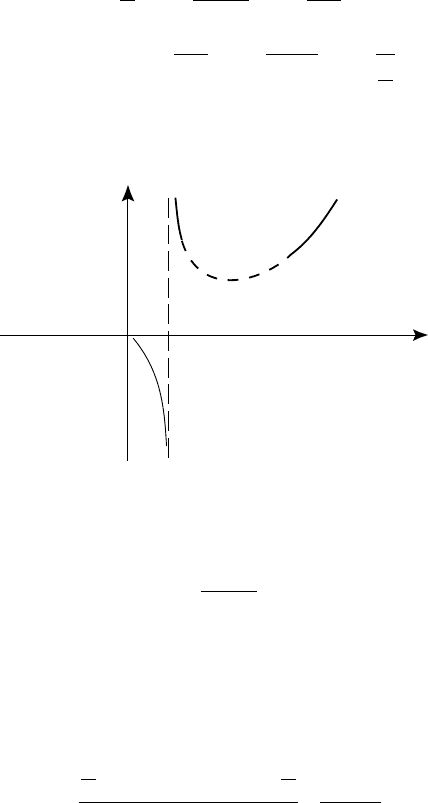
òîò íå èìååò òàêæå. Ïðèìåðíûé õîä ãðàôèêà èçîáðàæåí íà ðèñ. 27.
Èùåì ýêñòðåìóì ôóíêöèè. Åå ïðîèçâîäíàÿ:
x
x
y
2
ln
1ln
−
=
′
.
ó′= 0 ïðè x = e êðèòè÷åñêàÿ òî÷êà.
ó′ = ∞ ïðè x = 1 ãðàíè÷íàÿ òî÷êà, îíà íå ìîæåò áûòü ýêñòðå-
ìàëüíîé.
Èòàê, èìååì îäíó êðèòè÷åñêóþ òî÷êó x = e.
.
ln
ln2
ln
1
ln2)1(lnln
1
34
2
xx
x
x
x
xxx
x
y
−
=
⋅−−
=
′′
Ðèñ. 27
01
y
x
<
107
×òîáû ïðîâåðèòü, ÿâëÿåòñÿ ëè òî÷êà x = e ýêñòðåìàëüíîé,
íàéäåì çíàê y″ â òî÷êå x = e
.0
1
ln
ln2
)(
3
>=
−
=
′′
e
ee
e
ey
Çíà÷èò, òî÷êà x = e ÿâëÿåòñÿ òî÷êîé ìèíèìóìà ôóíêöèè. Çäåñü
ìû èñïîëüçîâàëè âòîðîå äîñòàòî÷íîå óñëîâèå ýêñòðåìóìà.
Îïðåäåëèì òî÷êè ïåðåãèáà ôóíêöèè:
y″ = 0 ïðè x = e
2
êðèòè÷åñêàÿ òî÷êà 2-ãî ðîäà;
y″ = ∞ ïðè x = 1, íî ýòà òî÷êà íå ÿâëÿåòñÿ êðèòè÷åñêîé òî÷êîé
2-ãî ðîäà, òàê êàê îíà ÿâëÿåòñÿ ãðàíè÷íîé òî÷êîé.
Ïðè ïðîõîæäåíèè ÷åðåç x = e
2
y″ ìåíÿåò çíàê ñ + íà , òàê êàê
,0
1
)( >=
′′
e
ey
à
;0
1
)(
3
3
<−=
′′
e
ey
çíà÷èò, çíà÷åíèå x = e
2
ÿâëÿåòñÿ
àáñöèññîé òî÷êè ïåðåãèáà,
.
2
)(
2
2
e
ey
=
Ñîñòàâèì òàáëèöó èçìåíåíèÿ çíàêîâ ïåðâîé è âòîðîé ïðîèç-
âîäíûõ.
x (0; 1) x = 1 (1; e) x = e (e; e
2
) x = e
2
(e
2
; ∞)
ó″(x) í.ñ. + + + 0
ó′(x) í.ñ. 0 + +
ó(x)
T ∩ í.ñ. T ∪ min = e R ∪ ò.ï. R ∩
2
2
e
y =
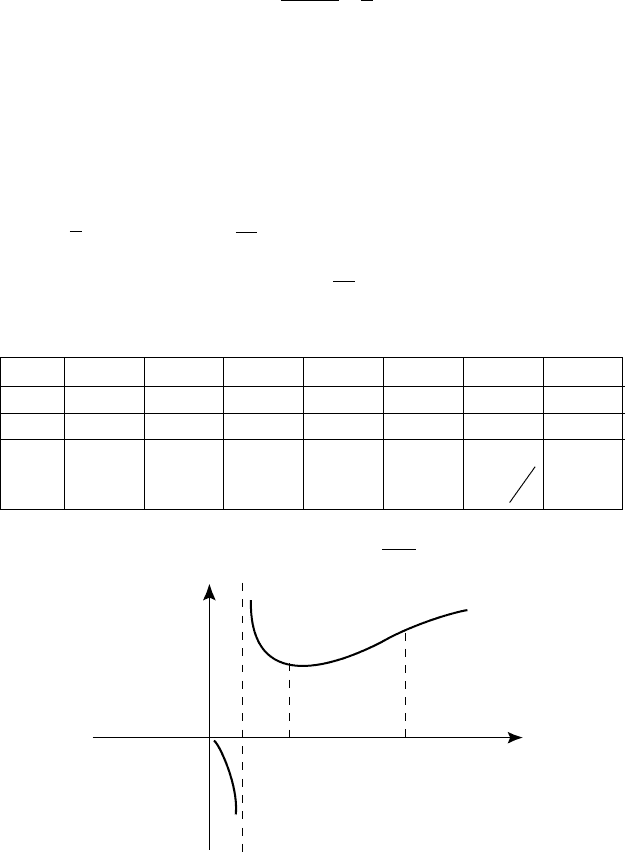
Îêîí÷àòåëüíûé ãðàôèê ôóíêöèè
x
x
y
ln
=
èçîáðàæåí íà ðèñ. 28.
Ðèñ. 28
01å å
2
y
x
<

108
Ïðèìåð 2.33. Èññëåäîâàòü è ïîñòðîèòü ãðàôèê ôóíêöèè
.
)
1
(
2
2
3
+
=
x
x
y
Ôóíêöèÿ ñóùåñòâóåò âñþäó, êðîìå õ = 1, ò.å. åå îáëàñòüþ îï-
ðåäåëåíèÿ ÿâëÿþòñÿ èíòåðâàëû (∞; 1), (1; ∞).
Íàéäåì òî÷êè ïåðåñå÷åíèÿ êðèâîé ñ îñÿìè êîîðäèíàò:
0
)1(2
2
3
=
+x
x
, ïðè õ = 0.
Îïðåäåëèì çíà÷åíèÿ ôóíêöèè íà ãðàíèöàõ îáëàñòè ñóùåñòâî-
âàíèÿ:
.
)1(2
limlim
;
02
1
)1(2
limlim
;
02
1
)1(2
limlim
;
)1(2
limlim
2
3
2
3
0101
2
3
0101
2
3
+∞=
+
=
−∞=
⋅
−
=
+
=
−∞=
⋅
−
=
+
=
−∞=
+
=
∞→∞→
+−→+−→
−−→−−→
−∞→
x
x
y
x
x
y
x
x
y
x
x
y
xx
xx
xx
x
Î÷åâèäíî, ïðÿìàÿ õ = 1 ÿâëÿåòñÿ âåðòèêàëüíîé àñèìïòîòîé
ôóíêöèè. Îïðåäåëèì íàêëîííûå àñèìïòîòû:
.1
242
2
lim
2
1
)1(2
lim)(lim
;
2
1
12
12
lim
)1(2
limlim
2
233
2
3
2
3
3
2
3
−=
++
−−−
=
−
+
=−=
=
++
=
+⋅
==
±∞→±∞→±∞→
±∞→±∞→±∞→
xx
xxxx
x
x
x
kxyb
x
x
x
x
xx
x
x
y
k
xxx
xxx
Èòàê, ïðÿìàÿ
1
2
1
−= xy
ÿâëÿåòñÿ íàêëîííîé àñèìïòîòîé êðè-
âîé, ïðè÷åì òî÷êè êðèâîé
2
3
)1(2
+
=
x
x
y
áóäóò íåîãðàíè÷åííî ïðè-
áëèæàòüñÿ ê ïðÿìîé
1
2
1
−=
xy
êàê ïðè õ → ∞, òàê è ïðè õ → ∞.
109
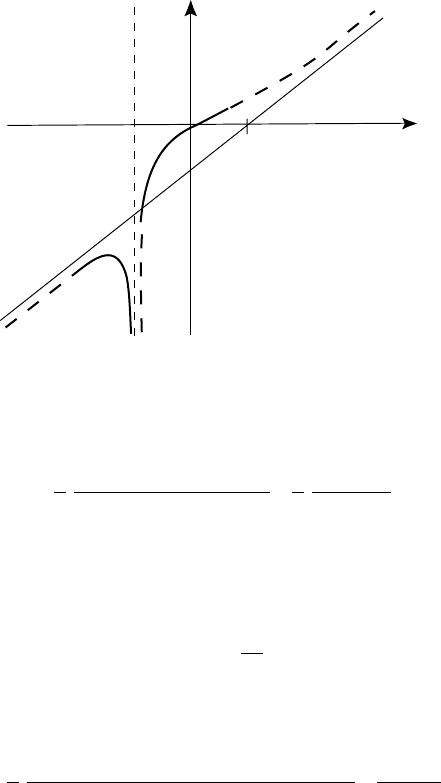
Íà ðèñ. 29 ïîñòðîåíà ïðîñòåéøàÿ êðèâàÿ, óäîâëåòâîðÿþùàÿ
ïðîâåäåííîìó èññëåäîâàíèþ.
Íàõîäèì ïðîèçâîäíûå:
.
)1(
)3(
2
1
)1(
)1(2)1(3
2
1
3
2
4
322
+
+
=
+
+−+
=
′
x
xx
x
xxxx
y
ó′ = 0 ïðè õ
1
= 3 è õ
1
= 0 êðèòè÷åñêèå òî÷êè 1-ãî ðîäà.
ó′ = ∞ ïðè õ = 1 ãðàíè÷íàÿ òî÷êà.
Ïðîâîäÿ îáû÷íîå èññëåäîâàíèå, íàõîäèì, ÷òî ïðè õ = 3 ôóí-
êöèÿ äîñòèãàåò ìàêñèìóìà
,
8
27
)3( −=−y
à â òî÷êå õ = 0 ýêñòðåìó-
ìà íåò, òàê êàê ïåðâàÿ ïðîèçâîäíàÿ ïðè ïðîõîæäåíèè ÷åðåç õ = 0
çíàê íå ìåíÿåò.
.
)1(
3
)1(
)1(3)3()1)(63(
2
1
46
22332
+
=
+
++−++
=
′′
x
x
x
xxxxxx
y
ó″ = 0 ïðè õ = 0 êðèòè÷åñêàÿ òî÷êà 2-ãî ðîäà.
ó″ = ∞ ïðè õ = 1 ãðàíè÷íàÿ òî÷êà.
Ðèñ. 29
0
1
x
y
1 1
110
Ñîñòàâèì òàáëèöó èçìåíåíèÿ çíàêîâ ïåðâîé è âòîðîé ïðîèç-
âîäíûõ.
x (∞; 3) x = 3 (3; 1) x = 1 (1; 0) õ = 0 (0; ∞)
ó″(x) í.ñ. 0 +
ó′(x) + 0 í.ñ. + 0 +
ó(x)
R ∩
8
27
max
−=
T ∩ í.ñ. R ∩ T ∪
Íàõîäèì, ÷òî õ = 0 ÿâëÿåòñÿ àáñöèññîé òî÷êè ïåðåãèáà ôóíê-
öèè, ïðè÷åì ó(0) = 0.
Ãðàôèê ÿâëÿåòñÿ âûïóêëûì íà èíòåðâàëàõ (∞; 1) è (1; 0)
è âîãíóòûì íà èíòåðâàëå (0; ∞).
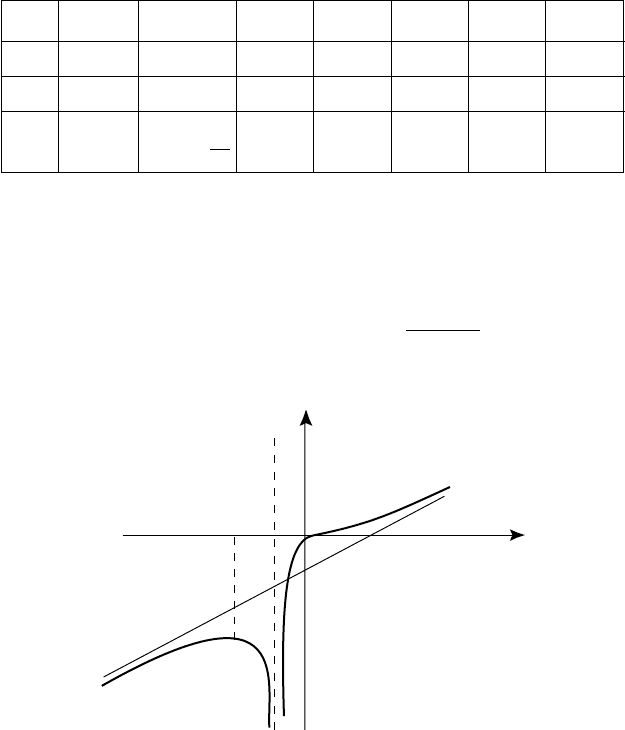
Îêîí÷àòåëüíûé ãðàôèê ôóíêöèè
2
3
)1(2
+
=
x
x
y
èçîáðàæåí íà
ðèñ. 30.
ò.ï.
y = 0
Ðèñ. 30
x
y
0
1
3 1 1
