Семенкин Е.С. Методы оптимизации. Практикум
Подождите немного. Документ загружается.


10. J(y
1
,y
2
)=
∫
−
+−
1
1
1
'
1
'
2
)2
2
1
(
23
dxxyyy
, y
1
(-1)=2, y
2
(-1)=-1, y
1
(1)=0, y
2
(1)=1
Отв.
=
−+−
=
x
xy
xx
xy
1
)(
6
)65(
)(
*
2
3
*
1
.
2.3. Функционалы, зависящие от производных высшего порядка
одной функции
Рассмотрим множество M допустимых функций y(x), m раз непрерывно
дифференцируемых на отрезке [ x
0
,x
1
], удовлетворяющих граничным
условиям
y(x
0
) = y
0
, y
(i)
(x
0
) = y
0
(i)
, i = 1,2,…,m-1,
y(x
1
) = y
1
, y
(i)
(x
1
) = y
1
(i)
, i = 1,2,…,m-1.
На множестве M задан функционал
∫
′
=
1
0
))(),...,(),(,())((
)(
x
x
m
dxxyxyxyxFxyJ ,
где функция F(x,y,y
′
,…,y
(m)
) дифференцируема ( m + 2) раза по всем
аргументам.
Среди допустимых кривых y(x), принадлежащих множеству M,
требуется найти кривую y
*
(x), на которой функционал достигает экстремума,
то есть
∫
′
=
∈
1
0
.))(),...,(),(,())((
)(
)(
*
x
x
m
Mxy
dxxyxyxyxFxyJ
extr
Искомая кривая является решением дифференциального уравнения
Эйлера – Пуассона
.0)1(...
)(
2
2
=−+++−
′′′
m
y
m
m
m
yyy
F
dx
d
F
dx
d
F
dx
d
F
Итак, для того чтобы применить необходимые условия экстремума в
поставленной задаче надо выполнить следующие действия.
1. Записать уравнение Эйлера-Пуассона.
2. Найти общее решение уравнения y = y(x,C
1
,…,C
2m
).
3. Определить постоянные С
1
, С
2
,…, С
2m
из граничных условий и
записать выражение для экстремали y
*
(x).
Пример 1. Найти экстремаль функционала
,)48())((
1
0
2
∫
−
′′
= dxyyxyJ
удовлетворяющую граничным условиям y(0) = 1, y
′
(0) = -4, y(1) = y
′
(1) = 0.
Составим уравнение Эйлера-Пуассона
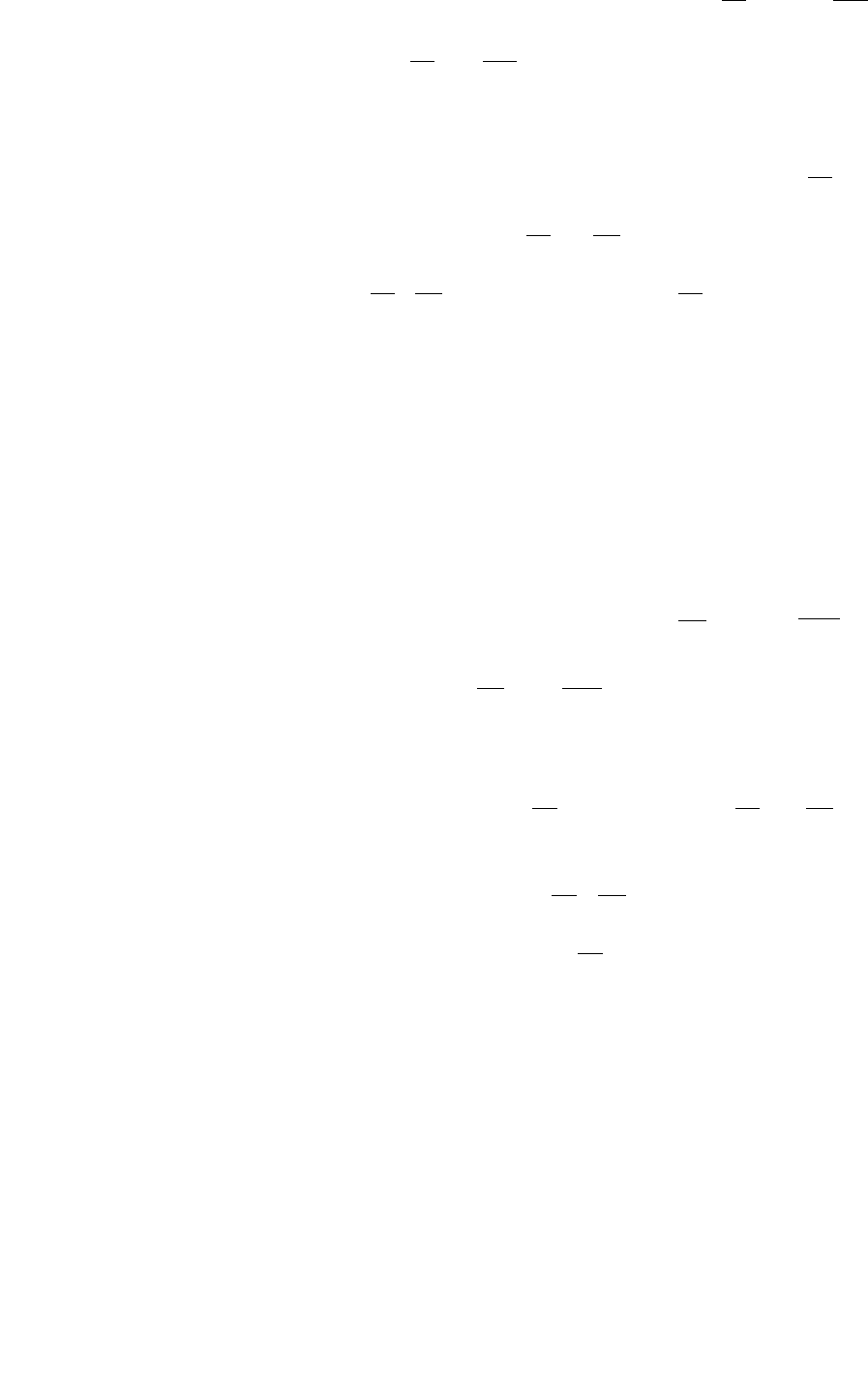
.24,0248
,2,0,2,0,48,48
)4()4(
2
2
)4(
2
2
2
==+−=+−
==
′′
==−=−
′′
=
′′′
′′′′′′
yyF
dx
d
F
dx
d
F
yF
dx
d
F
dx
d
yFFFyyF
yyy
yyyyy
Решим дифференциальное уравнение, определим константы и запишем
уравнение экстремали.
.1464)(
,1,4,12,24
,4)0(,1)0(
0
2
4)1(,0
26
1)1(
,
26
)(
,
2
4)(,12)(,24)(
234*
4321
34
32
1
43
21
43
2
2
3
1
4
32
2
1
3
21
2
1
+−+−=
=−==−=
−==
′
==
=+++=
′
=++++=
++++=
+++=
′
++=
′′
+=
′′′
xxxxxy
CCCC
CyCy
CC
C
yCC
CC
y
CxCx
C
x
C
xxy
CxCx
C
xxyCxCxxyCxxy
y
*
(x)=e
x
.
Пример 2. Найти экстремаль функционала J(y(x))=
∫
1
0
''
)( dxxy
,
удовлетворяющую граничным условиям y(0)=y
’
(0)=y
’
(1)=0, y(1)=1.
Составим уравнение Эйлера-Пуассона:
2
''
yF =
, F
y
=0,
0
'
=
y
F
,
''
2
''
yF
y
=
,
0
'
=
y
F
dx
d
,
)4(
2
2
2
''
yF
dx
d
y
=
,
02
)4(
2
2
'''
==+− yF
dx
d
F
dx
d
F
yy
y
Решим дифференциальное уравнение, определим константы и запишем
уравнение экстремали
y
’’’
=C
1
, y
’’
=C
1
x+C
2
, y
’
=
32
2
1
2
CxCx
C
++
,
43
2
2
3
1
2
6
CxCx
C
x
C
y +++=
,
y(0)=C
4
=0, y
’
(0)=C
3
=0,
1
2
6
)1(
43
21
=+++= CC
CC
y
,
0
2
)1(
32
1
'
=++= CC
C
y
,
C
1
=-12, C
2
=6, C
3
=0, C
4
=0,
y
*
(x)=-2x
3
+3x
2
.
Пример 3.
Найти экстремаль функционала J(y(x))=
∫
−
1
0
''
)(
2
dxxye
x
,
Удовлетворяющую граничным условиям y(0)=y
’
(0)=1, y(1)=y
’
(1)=e
cоставим уравнение Эйлера-Пуассона:
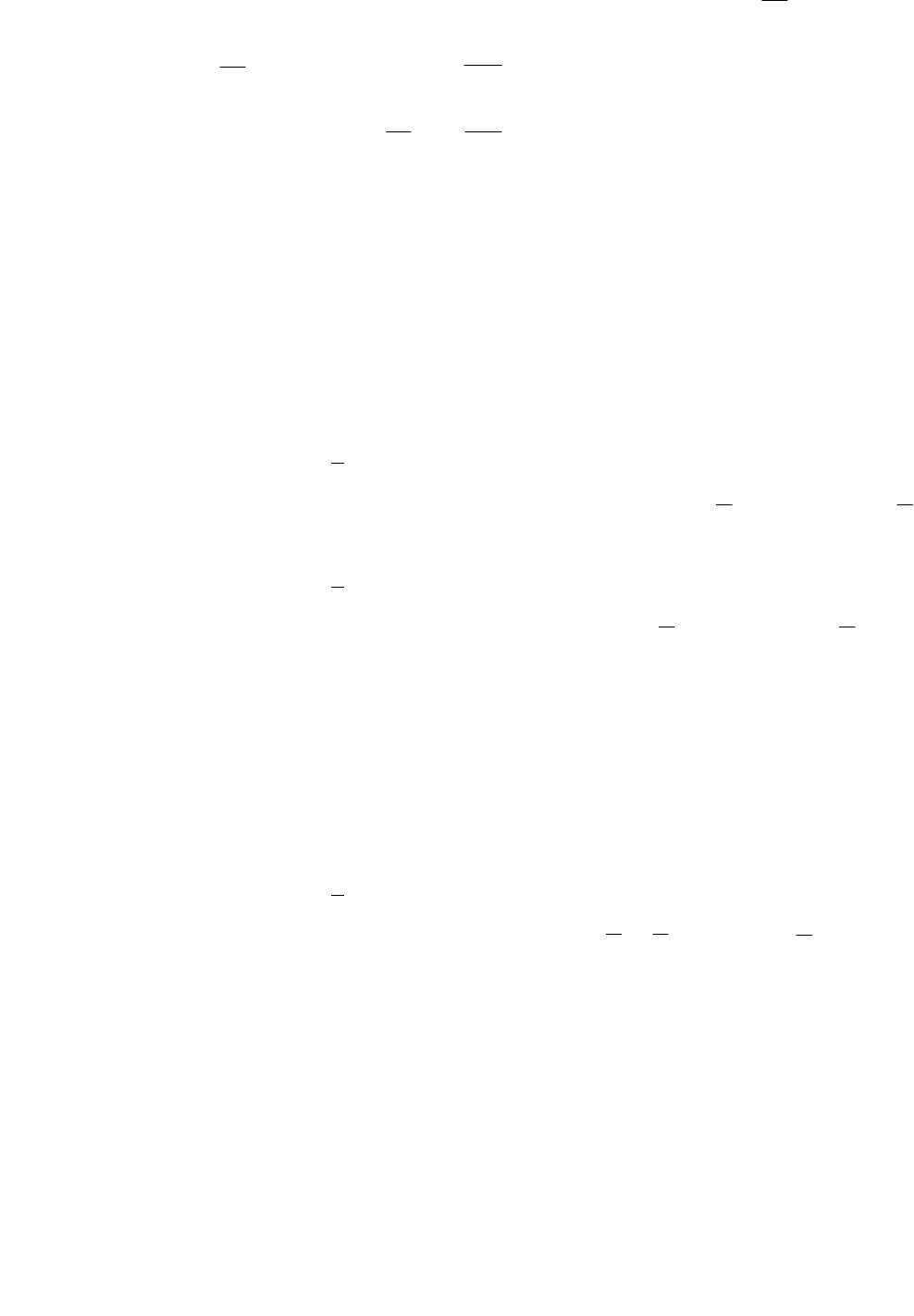
2
''
yeF
x−
=
, F
y
=0,
0
'
=
y
F
,
x
y
eyF
−
=
''
2
''
,
0
'
=
y
F
dx
d
,
xx
y
eyeyF
dx
d
−−
−=
'''''
22
'' ,
xxxx
y
eyeyeyeyF
dx
d
−−−−
+−−=
'''''''')4(
2
2
2222
''
,
0)2(2
''''')4(
2
2
'''
=+−=+−
−
yyyeF
dx
d
F
dx
d
F
x
yy
y
y
(4)
-2y
’’’
+y
’’
=0
Решим дифференциальное уравнение, определим константы и запишем
уравнение экстремали
y(x)=C
1
+C
2
x+C
3
e
x
+C
4
xe
x
.
y(0)=C
1
+C
3
=1, y
’
(0)=C
2
+C
3
+C
4
=1
y(1)=C
1
+C
2
+C
3
e+C
4
e=e
y
’
(1)=C
2
+C
3
e+2C
4
e=e
Отсюда получаем C
1
=C
2
=C
4
=0, C
3
=1.
Найти экстремали функционалов, зависящих от производных высшего
порядка одной функции.
1. J(y(x))=
∫
−
+−
4
0
2''
)16(
2
π
dxxeyy
x
, y(0)=1, y(
4
π
)=0, y
’
(0)=0, y
’
(
4
π
)=-2.
Отв. y
*
=cos(2x).
3. J(y(x))=
∫
+−
2
0
22''
)(
2
π
dxxyy
, y(0)=1, y(
2
π
)=0, y
’
(0)=0, y
’
(
2
π
)=-1. Отв.
y
*
=cos(x).
4. J(y(x))=
∫
+
1
0
'''
)3(
2
dxyyy
, y(0)=0, y(1)=2, y
’
(0)=0, y
’
(1)=5. Отв.
y
*
=x
3
+x
2
.
5. J(y(x))=
∫
−
1
0
''
)48(
2
dxyy
, y(0)=0, y(1)=1, y
’
(0)=0, y
’
(1)=4. Отв. y
*
=x
4
.
6. J(y(x))=
∫
−
2
0
'''
)(
22
π
dxyy
, y(0)=1, y(
2
π
)=
2
π
, y
’
(0)=1, y
’
(
2
π
)=0. Отв.
y
*
=x+cos(x).
7. J(y(x))=
∫
−
1
0
''
2
dxye
x
, y(0)=0, y(1)=e, y
’
(0)=1, y
’
(1)=2e. Отв. y
*
=xe
x
.
8. J(y(x))=
∫
1
0
'''
2
dxy
, y(0)= y
’
(0)=y
’’
(0)=1, y(1)=1, , y
’
(1)=4, y
’’
(1)=12.
Отв. y
*
=x
4
.

9. J(y(x))=
∫
++
1
0
'''2
)21(
2
dxyx
, y(0)=1, y
’
(0)=0, y
’’
(0)=-2, y(1)=2,
y
’
(1)=6, y
’’
(1)=22. Отв. y
*
=2x
4
-x
2
+1.
10. J(y(x))=
∫
+
1
0
'''
)(
22
dxyy
, y(0)=0, y(1)=e-2, y
’
(0)=0, y
’
(1)=e-1. Отв.
y
*
=e
x
-x-1.
11. J(y(x))=
∫
+
1
0
'''
)4(
22
dxyy
, y(0)=0, y(1)= )3(
4
1
2
−e , y
’
(0)=0, y
’
(1)=
)1(
2
1
2
−e . Отв. y
*
= )12(
4
1
2
−− xe
x
.
12. J(y(x))=
∫
+−
2
0
2'''
)2(
22
π
dxyyy
, y(0)=0, y(
2
π
)=
2
π
, y
’
(0)=0, y
’
(
2
π
)=1.
2.4. Метод вариаций с подвижными границами
Рассмотрим множество M допустимых функций y(x), удовлетворяющих
следующим условиям:
а) функции y(x) непрерывно дифференцируемые на некотором
конечном отрезке, внутренними точками которого являются значения x
0
x
1
,
которые заранее не заданы,
б) значения x
0
, y
0
= y(x
0
) и x
1
, y
1
= y(x
1
), определяющие концы
допустимых кривых, удовлетворяют граничным условиям
ψ(x
0
, y
0
) = 0, φ(x
1
, y
1
) = 0,
где ψ(x, y), φ(x, y) заданные непрерывно дифференцируемые функции.
На множестве M задан функционал
,))(),(,())((
1
0
∫
′
=
x
x
dxxyxyxFxyJ
где функция F( x, y, y
′
) имеет непрерывные частные производные до второго
порядка включительно по всем переменным.
Среди допустимых кривых y(x), принадлежащих множеству M,
требуется найти кривую y
*
(x), на которой функционал достигает экстремума
.))(),(,())((
1
0
)(
*
∫
′
=
∈
x
x
Mxy
dxxyxyxFxyJ
extr
(1)
В такой постановке задачи экстремум функционала ищется в классе
гладких кривых, концы которых скользят по двум заданным линиям. Можно
выделить частные случаи общей постановки задачи: 1) концы допустимых
кривых скользят по двум заданным вертикальным прямым, описываемым
уравнениями x = x
0
, x = x
1
, 2) концы допустимых кривых скользят по двум
заданным кривым, описываемым уравнениями y = ψ(x), y = φ(x).

В поставленной задаче наряду с поиском кривой y
*
(x) производится
выбор значений x
0
*
, x
1
*
, то есть ищется тройка (y
*
(x), x
0
*
,x
1
*
). Функционал
достигает на тройке (y
*
(x), x
0
*
,x
1
*
) минимума, если J((y(x), x
0
,x
1
) ≥ J((y
*
(x),
x
0
*
,x
1
*
) в ε-окрестности.
В силу наличия граничных условий вариации δy(x
1
) δx
1
, δy(x
0
), δx
0
связаны соотношениями
,0)()(
11
*
1
*
1
=
′
−+
=
′
=
′
xFyFxyF
xx
y
xx
y
δδ
,0)()(
00
*
0
*
0
=
′
−+
=
′
=
′
xFyFxyF
xx
y
xx
y
δδ
которые называются условиями трансверсальности.
Если на функции y
*
(x), удовлетворяющей граничным условиям:
ψ(x
0
, y
0
) = 0, φ(x
1
, y
1
) = 0,
функционал достигает экстремума, то она удовлетворяет уравнению Эйлера
и условиям трансверсальности.
Для решения задачи (1) надо выполнить следующие действия.
1. Записать уравнение Эйлера и найти общее решение этого уравнения
y = y(x,C
1
,C
2
).
2. Записать условия трансверсальности в зависимости от вида
граничных условий.
3. Из условий трансверсальности и граничных условий определить C
1
,
C
2
, x
0
*
, x
1
*
и получить уравнение экстремали y
*
(x).
Пример 1. Найти кривую, на которой функционал
∫
′
+
′
+=
2
0
2
)2())(( dxyyyxyxyJ
может достигать экстремума, если ее левый конец фиксирован в точке А(0,0),
а правый лежит на прямой x = x
1
= 2.
Составим уравнение Эйлера
.0
,2,2,2,2
2
=−
′′
=−
′′
+
′
=
′
+=
′
+=
′
+
′
+=
′
′′
xyF
dx
d
F
yyF
dx
d
yyFyxFyyyxyF
yy
yyy
Найдем общее решение дифференциального уравнения
.
6
)(,
2
)(
21
3
1
2
CxC
x
xyC
x
xy ++=+=
′
Запишем условия трансверсальности на правом конце и граничные
условия на левом конце
.0)0(,0)2(2)2(2
2121
==
′
+=
′
+=
==
′
yyyyyF
xxy
Из этих условий определим константы C
1
и C
2
и запишем экстремаль
.
3
4
6
)(,0,
3
4
3
*
21
x
x
xyCC −==−=
Пример 2. Найти кривую на которой функционал
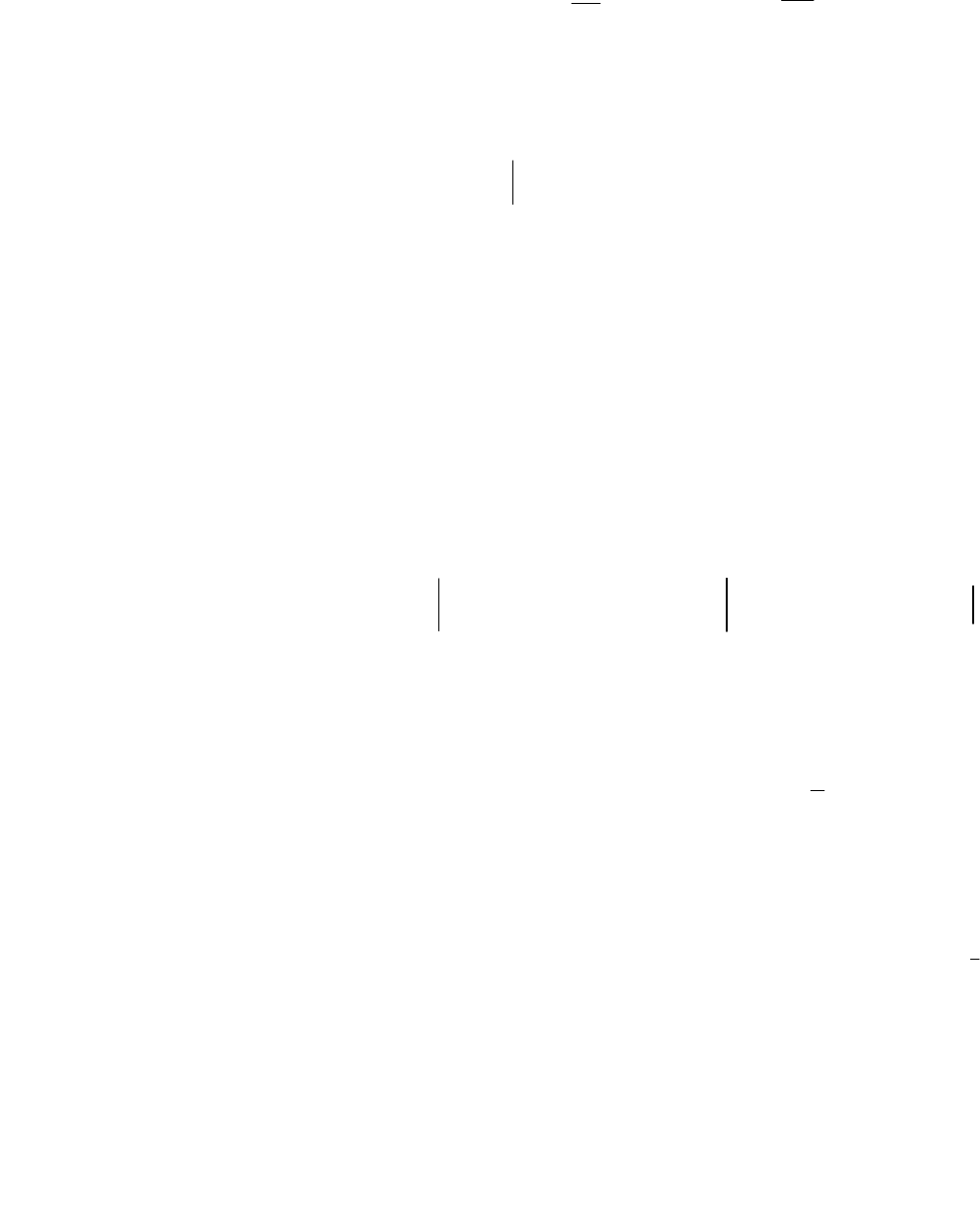
J(y(x))=
∫
+
1
0
'
)(
2
dxyy
может достичь экстремума, если правый ее конец фиксирован в точке В(1,0),
а левый лежит на прямой х=0.
Составим уравнение Эйлера:
yyF +=
2
'
, F
y
=1,
'
2
'
yF
y
=
,
''
2
'
yF
dx
d
y
=
,
021
''
'
=−=− yF
dx
d
F
y
y
Найдем общее решение уравнения Эйлера
y
’’
=½, y
’
=½x+C
1
, y=¼x
2
+C
1
x+C
2
.
Запишем условие трансверсальности на левом конце и граничное
условие на правом конце
0)0(2
'
0
0
'
==
=
yF
x
y
, y(1)=0.
Из этих условий определим константы C
1
и C
2
.
y
’
(0)=C
1
=0
y(1)=¼+C
1
+C
2
=0
C
1
=0, C
2
=-¼, y
*
(x)=¼(x
2
-1).
Пример 3. Найти кривую, на который функционал J(y(x))=
∫
1
3
0
'
x
dxy
может достигать экстремума, если её левый конец фиксирован в точке А(0,0),
а правый находится на прямой y(x
1
)=1-x
1
.
Так как подынтегральная функция не зависти от x и y, то уравнение
Эйлера имеет общее решение y(x)=C
1
x+C
2
.
Запишем условие трансверсальности
0)32(3)1()(
1
2
1
23
1
'
'''''''
=+−=+−=−+
=
=
=
xx
xx
xx
y
yyyyyFyF ϕ
И граничное условия y(0)=0, y(x
1
)=1-x
1
Из этих условий найдем C
1
, C
2
, x
1
*
.
y(0)=C
2
=0 y(0)=C
2
=0
y
’
(0)=C
1
=0 y
’
(0)=C
1
=
2
3
−
y(x
1
)=C
1
x
1
+C
2
=1-x
1
y(x
1
)=C
1
x
1
+C
2
=1-x
1
Из первой системы находим C
1
=C
2
=0, x
1
*
=1, а из второй C
1
=-3/2, C
2
=0,
x
1
*
=-2.
В результате получим две экстремали y
1
*
(x)=0, y
2
*
=-3/2 x.
Пример 4. Найти кривую, на которой функционал J(y(x))=
∫
+
1
0
2
2
1
'
)1(
x
x
dxy
может достичь экстремума, если ее левый конец лежит на кривой:
y(x)= ψ(x)=x
2
+2,
а правый конец – на кривой y(x)=φ(x)=x.
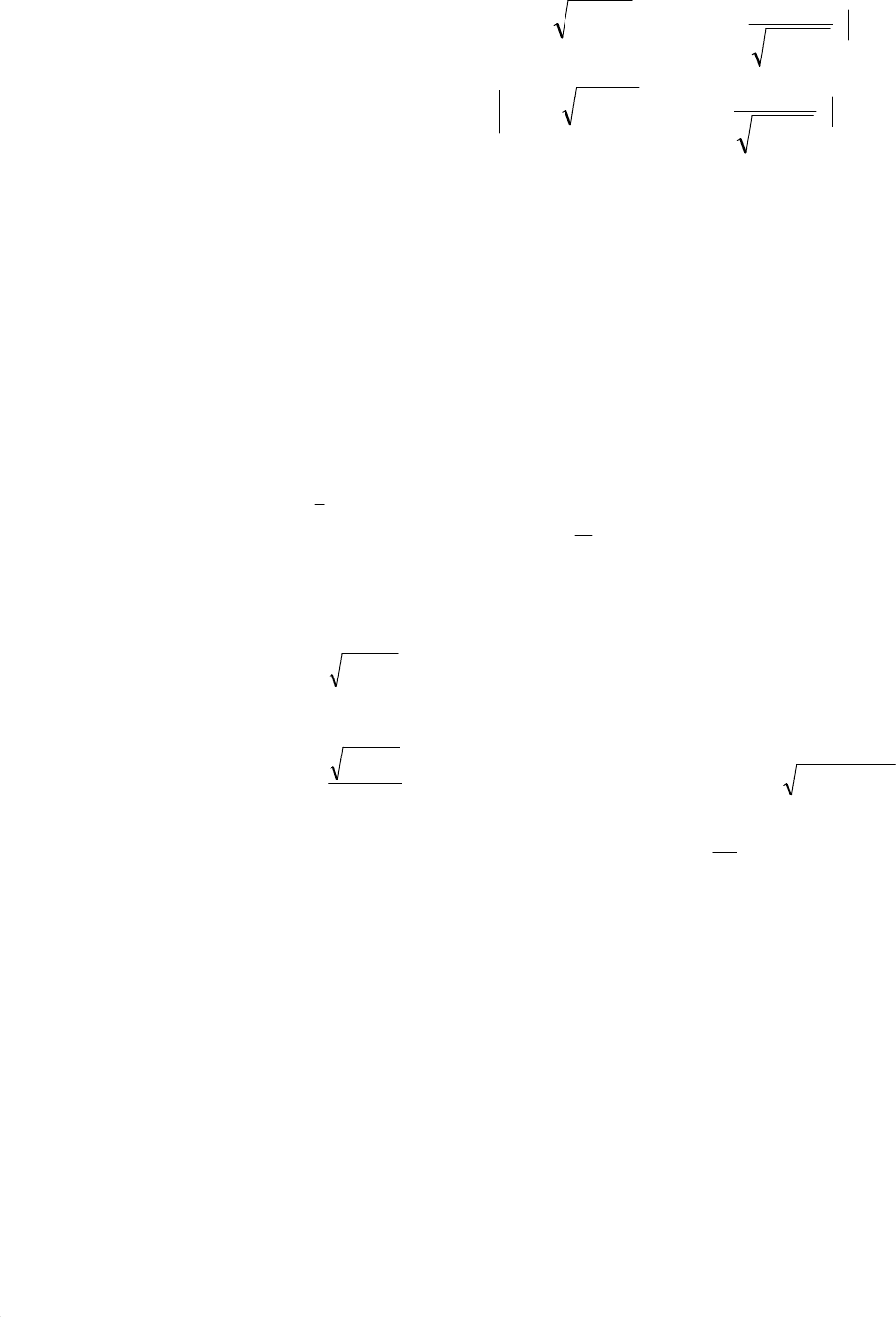
Так как подынтегральная функция не зависит явно от x и y , то
уравнение Эйлера имеет общее решение y(x)=C
1
x+C
2
.
Запишем условия трансверсальности и граничные условия
0
1
)2(1)(
0
2
2
0
'
'
'
''''
=
+
−++=−+
=
=
xx
xx
y
y
y
yxyFyF ψ
,
0
1
)1(1)(
1
2
2
1
'
'
'
''''
=
+
−++=−+
=
=
xx
xx
y
y
y
yyFyF ϕ
.
y(x
0
)=C
1
x
0
+C
2
= ψ(x
0
)=x
0
2
+2,
y(x
1
)=C
1
x
1
+C
2
= φ(x
1
)=x
1.
Из этих условий найдем C
1
, C
2
, x
1
*
, x
0
*
.
1+2x
0
y
’
(x
0
)=1+2x
0
C
1
=0,
1+y
’
(x
1
)=1+C
1
=0,
C
1
x
0
+C
2
=x
0
2
+2,
C
1
x
1
+C
2
=x
1.
C
1
=-1, x
0
*
=1/2, C
2
=11/4, x
1
*
=11/8.
В результате получим экстремаль y
*
(x)=-x+11/4.
Найти экстремали функционалов с подвижными границами
1. J(y(x))=
∫
−
4
0
2'
)(
2
π
dxyy , y(0)=1, x
1
=
4
π
. Отв. y
*
(x)=cos(x)+sin(x).
2. J(y(x))=
∫
1
2
0
'
x
dxy
, y(0)=0,y( x
1
)=-x
1
-1. Отв. y
*
(x)=-2x
1
, x
1
*
=1.
3. J(y(x))=
∫
+
1
0
2
'
1
x
x
dxy , y(x
0
)=t
0
2
,y( x
1
)=x
1
-5. Отв. y
*
(x)=-x
1
+3/4, x
1
*
=23/8,
x
0
*
=1/2.
4. J(y(x))=
∫
+
1
2
0
'
1
x
dx
y
y
, y(0)=1, y( x
1
)=x
1
-1. Отв. y
*
(x)=
2
)1(2 −− x , x
1
*
=2.
5. J(y(x))=
∫
−
1
0
''
)( dxxyy
, x
0
=0 , x
1
=1. Отв. y
*
(x)=
C
x
+
4
2
6. J(y(x))=
∫
1
0
'
2
dxy
, y(0)=0, y(1)=1. (отв. y
*
(x)=x )
7. J(y(x))=
∫
−
1
0
''
)(
2
dxyxy
, y(0)=1, y(1)=1/4. (отв. y
*
(x)=x
2
/4-x+1 )
8. J(y(x))=
∫
+
2
1
2'2
)12(
2
dxyyx
, y(1)=1, y(2)=8. (отв. y
*
(x)=x
3
)
9. J(y(x))=
∫
−
8
4
2
)4( dxyx , y(4)=1, y(8)=2. (отв. y
*
(x)=x/4 )

10. J(y(x))=
∫
−
4
2
''
)2(
34
dxyyxy
, y(2)=1, y(4)=5. (отв. y
*
(x)=2x-3 )
11. J(y(x))=
∫
−
2
0
''
)3(
23
dxyyxy
, y(0)=4, y(2)=6. (отв. y
*
(x)=x+4 )
12. J(y(x))=
∫
++
1
0
2''
)243(
2
dxyxyyy
, y(0)=1, y(1)=0. (отв. y
*
(x)=x
4
-2x+1 )
13. J(y(x))=
∫
++
1
0
''
)1(
2
dxyy , y(0)=1, y(1)=2. (отв. y
*
(x)=x+1 )
14. J(y(x))=
∫
−
e
dxyxy
1
''
)2(
2
, y(1)=1, y(e)=2. (отв. y
*
(x)=ln(x)+1 )
16. J(y(x))=
∫
+
2
1
2'
)( dxyxy
, y(1)=1, y(2)=1/2. (отв. y
*
(x)=1/x )
17. J(y(x))=
∫
++
2
1
2
'
)
)ln(2
(
2
dx
x
xy
x
y
xy , y(1)=0, y(2)=1-ln(2). (отв. y
*
(x)=
)ln()
1
(
3
2
x
x
x −− )
18. J(y(x))=
∫
++
2
1
'
3
2
)8
3
(
2
dxy
x
y
x
y
, y(1)=0, y(2)=8ln(2). (отв. y
*
(x)=x
3
ln(x) )
19. J(y(x))=
∫
+
2
1
''
)2(
2
dxyyxy
, y(1)=0, y(2)=ln(2). (отв. y
*
(x)=ln(x) )
20. J(y(x))=
∫
−
−
+
1
2
2'3
)3(
2
dxxyyx
, y(-2)=15/8, y(-1)=0. (отв. y
*
(x)= x
x
−
3
1
)
21. J(y(x))=
∫
+++
2
1
'22'
))1()(( dxyxyxy
, y(1)=-1/2, y(2)=1. (отв. y
*
(x)=
x
x
2
1
2
1
−+ )
3. Вариационные задачи поиска условного экстремума
3.1. Задачи на условный экстремум с конечными связями
Рассмотрим множество M допустимых функций y
1
(x), y
2
(x),…,y
n
(x),
непрерывно дифференцируемых на отрезке [ x
0
, x
1
], удовлетворяющих
граничным условиям y
i
(x
0
) = y
i0
, y
i
(x
1
) = y
i1,
i = 1,2,…,n и конечным связям
φ
j
(x, y
1
(x), y
2
(x),…,y
n
(x)) = 0, j = 1,2,…,m,
где функции φ
j
(x, y
1
(x), y
2
(x),…,y
n
(x)) непрерывно дифференцируемы по всем
переменным.
На множестве M задан функционал
∫
′′
=
1
0
))(),...,(),(),...,(,())(),...(),((
1121
x
x
nnn
dxxyxyxyxyxFxyxyxyJ ,

где подынтегральная функция имеет непрерывные частные производные до
второго порядка включительно по всем переменным.
Среди допустимых функций требуется найти функции
)(),...,(),(
**
2
*
1
xyxyxy
n
,
на которых функционал достигает экстремума.
Поставленная задача относится к задачам поиска условного
экстремума, так как кроме граничных условий на искомые функции
наложены дополнительные условия.
Искомые экстремали в этом случае удовлетворяют системе уравнений
Эйлера, niL
dx
d
L
ii
yy
,...2,1,0 ==−
′
, составленной для функционала
∫
′′
=
1
0
))(),...,(,,...,,,...,,(),...,,(
11121
x
x
mnnn
dxxxyyyyxLyyyJ λλ
где
∑
=
+
′′
=
′′
m
j
njjnnmnn
yyxxyyyyxFxxyyyyxL
1
111111
),...,,()(),...,,,...,,())(),...,(,,...,,,...,,( ϕλλλ .
Функция L(x,y
1
,y
2
,…,y
n
,y
1
′
,…,y
n
′
,λ
1
(x),…,λ
m
(x)) называется функцией
Лагранжа, а λ
j
(x) множителями Лагранжа.
Для того чтобы применить необходимые условия экстремума в
поставленной задаче надо выполнить следующие действия.
1. Составить функцию Лагранжа.
2. Записать систему уравнений Эйлера для функции Лагранжа и
условия связи
niL
dx
d
L
ii
yy
,...2,1,0 ==−
′
,
φ
j
(x, y
1
(x), y
2
(x),…,y
n
(x)) = 0, j = 1,2,…,m.
3. Найти общее решение системы уравнений Эйлера.
4. Определить постоянные C
1
,…,C
2n
из граничных условий, решая
систему
y
i
(x
0
, C
1
,…, C
2n
) = y
i0
, i = 1,2,…,n,
y
i
(x
1
, C
1
,…, C
2n
) = y
i0
, i = 1,2,…,n,
и выражения для множителей Лагранжа λ
j
(x), j = 1,2,…,m.
В результате получить экстремали )(),...,(),(
**
2
*
1
xyxyxy
n
, на которых может
достигаться экстремум функционала.
Пример 1. Найти экстремаль функционала
1)
2
(,1)
2
(,1)0(,1)0(
,)(),(
2121
2
0
2
2
2
1
2
2
2
121
==−==
′
−
′
−+=
∫
ππ
π
yyyy
dxyyyyyyJ
удовлетворяющую уравнению связи y
1
– y
2
– cosx = 0.
Cоставим функцию Лагранжа
).cos2)(())(,,,(
21
2
2
2
1
2
2
2
121
xyyxyyyyxyyxL −−+
′
−
′
−+= λλ

Запишем систему уравнений Эйлера и уравнение связи
.0cos2
,02)(2
,02)(2
21
22
11
22
11
=−−
=
′′
+−=−
=
′′
++=−
′
′
xyy
yxyL
dx
d
L
yxyL
dx
d
L
yy
yy
λ
λ
Найдем общее решение системы и определим произвольные
постоянные из граничных условий
.2,0,1
2
)
2
(,11
2
)0(
).(2)(2)(
,cos2)()(
,cossin
2
cos
2
)(
21
2
1
1
1
22
12
21
1
=====+=
′′
+=
−=
++=
CC
C
y
C
y
xyxyx
xxyxy
xx
C
x
C
xy
π
λ
Граничные условия и уравнение связи согласованы. Запишем
полученные экстремали
.cossin)(,cossin)(
*
2
*
1
xxxyxxxy −=+=
3.2. Задачи на условный экстремум с дифференциальными связями
Рассмотрим множество M допустимых функций y
1
(x), y
2
(x),…,y
n
(x),
непрерывно дифференцируемых на отрезке [ x
0
, x
1
], удовлетворяющих
граничным условиям y
i
(x
0
) = y
i0
, y
i
(x
1
) = y
i1
, i = 1,2,…,n и дифференциальным
связям
,,...,2,1,0))(),...,(),(),...,(,(
11
mjxyxyxyxyx
nnj
==
′
′
ϕ
где функции
))(),...,(),(),...,(,(
11
xyxyxyxyx
nnj
′
′
ϕ
непрерывно дифференцируемы по
всем переменным.
На множестве M задан функционал
∫
′′
=
1
0
))(),...,(),(),...,(,())(),...(),((
1121
x
x
nnn
dxxyxyxyxyxFxyxyxyJ ,
где подынтегральная функция имеет непрерывные частные производные до
второго порядка включительно по всем переменным.
Среди допустимых функций требуется найти функции
)(),...,(),(
**
2
*
1
xyxyxy
n
, на которых функционал достигает экстремума.
Поставленная задача относится к задачам поиска условного
экстремума, так как кроме граничных условий на искомые функции
наложены дополнительные условия.
Искомые экстремали в этом случае удовлетворяют системе уравнений
Эйлера, niL
dx
d
L
ii
yy
,...2,1,0 ==−
′
,
составленной для функционала
∫
′′
=
1
0
))(),...,(,,...,,,...,,(),...,,(
11121
x
x
mnnn
dxxxyyyyxLyyyJ λλ
