Семенкин Е.С. Методы оптимизации. Практикум
Подождите немного. Документ загружается.


x
0
= (0, 10) f(x
0
) = 100
Исследующий поиск
x
1
= (0, 9.5) f(x
1
) = 90,25
Поиск по образцу
x
3
= (0, 8) f(x
3
) = 64
Поиск по образцу
x
4
= (0, 4.5) f(x
4
) = 20,25
Поиск по образцу
x
5
= (0, -2) f(x
5
) = 4
Исследующий поиск
x
6
= (0, -1.5) f(x
6
) = 2,25
Исследующий поиск с уменьшением шага
x
7
= (0, 0) f(x
7
) = 0
Наименьшее значение функции достигается а точке (0, 0) с точностью ε
= 0,1.

Глава 4. Вариационное исчисление
1. Постановка задачи
На практике существуют задачи оптимизации, в которых не удается
описать качество выбранного решения с помощью целевой функции. В этих
задачах критерий качества зависит от функции, определить которую
необходимо так, чтобы критерий принял минимальное или максимальное
значение.
Вариационными задачами называются задачи о поиске экстремума
функционалов, то есть величин, численное значение которых определяется
выбором одной или нескольких функций.
Переменная J(y(x)) называется функционалом, зависящим от функции
y(x), если каждой кривой из заданного класса функций M соответствует
вполне определенное действительное значение J.
Пример 1. Найти значение функционала
∫
=
1
0
)())(( dxxyxyJ
на следующих
кривых y
1
(x) = x, y
2
(x) = x
2
, y
3
(x) = - (x – 1)
2
+1.
Найдем значения функционала, соответствующие приведенным
функциям J(y
1
(x) = ½, J(y
2
(x) = 1/3, J(y
3
(x) = 2/3.
В данном примере функционал имеет простой смысл – площадь под
кривой y(x). Каждой кривой поставлено в соответствие число, равное
площади. Очевидно, можно поставить задачу о нахождении такой кривой,
площадь под которой была бы минимальна (максимальна). В рассмотренном
примере такой кривой является y
3
(x).
Приведем основные понятия, которые будут использоваться в этой
главе.
Функции, на которых сравниваются значения функционалов,
называются допустимыми функциями.
Вариацией δy(x) аргумента y(x) функционала J(y(x)) называется
разность допустимых функций функционала δy(x) = y
1
(x) – y(x).
Приращением ∆J функционала называется разность:
∆J = ∆J(δy) = J(y +δy) – J(y).
Главную часть приращения функционала, линейную относительно
вариации аргумента, называют вариацией функционала и обозначают δJ.
Пример 2. Найти вариацию функционала J(y(x))=
∫
1
0
'
x
x
dxyy .
По определению приращения функционала имеем
∆J=J(y(x)+δy(x))-J(y(x))=
∫ ∫
−++
1
0
1
0
'''
))((
x
x
x
x
dxyydxyyyy δδ =
∫ ∫
++
1
0
1
0
'''
)(
x
x
x
x
dxyydxyyyy δδδδ ,
Откуда искомая вариация равна:

δJ(y(x))=
∫
+
1
0
)(
''
x
x
dxyyyy δδ
Пример 3. Найти вариацию функционала J(y(x))=
∫
b
a
dxxy )(
2
.
Запишем приращение функционала
∆J=
∫
+
b
a
dxxyxy
2
))()(( δ -
∫
b
a
dxxy )(
2
=
∫
b
a
dxxyxy )()(2 δ +
∫
b
a
dxxy
2
))((δ
Откуда искомая вариация равна
δJ(y(x))=
∫
b
a
dxxyxy )()(2 δ .
Функционал J(y(x)), определенный на классе M кривых y(x), достигает
на кривой y
*
(x) глобального минимума (максимума), если
J(y
*
(x)) ≤ J(y(x)) (J(y
*
(x)) ≥ J(y(x)))
для любой кривой y(x) принадлежащей M.
Теорема 1.(Необходимые условия экстремума). Если функционал
J(y(x)), имеющий вариацию, достигает минимума или максимума на кривой
y
*
(x), где y
*
(x) есть внутренняя точка области определения функционала, то
при y(x) = y
*
(x) первая вариация функционала равна нулю δJ = 0.
Найти вариацию функционала
1. J(y(x))=
∫
+
e
i
dxxyyy
1
'
)(
2
, если y=ln(x), δy=
1
)1(
−
−
e
x
α
Ответ: δJ=3α.
2. J(y(x))=
∫
+
1
0
'2
)(
2
dxyy
Ответ: δJ=
∫
−
1
0
''
)22( ydxyy δ
3. J(y(x))=
∫
−
−
0
1
'
)12(
2
dxyxy
Ответ: δJ=
∫
−
+
0
1
''
)212( ydxyx δ
4. J(y(x))=
∫
−
2
0
2'
)(
2
π
dxyy
Ответ: δJ=
∫
−−
2
0
''
)22(
π
δydxyy
2. Вариационные задачи поиска безусловного экстремума

2.1. Функционалы, зависящие от одной функции
На множестве M задан функционал
∫
′
=
1
0
,))(),(,())((
x
x
dxxyxyxFxyJ
где подынтегральная функция F(x,y,y
′
) имеет непрерывные частные
производные до второго порядка включительно по всем переменным.
Среди допустимых кривых y(x), принадлежащих множеству M,
требуется найти кривую y
*
(x), на которой функционал достигает экстремума,
то есть
.))(),(,())((
1
0
)(
*
∫
′
=
∈
x
x
Mxy
dxxyxyxFxyJ
extr
(1)
Так как на кривые y(x), образующие множество M , не наложено
дополнительных условий, кроме граничных, то поставленная задача
называется задачей поиска безусловного экстремума.
Стратегия поиска решения задачи (1) состоит в определении первой
вариации δJ функционала J(y(x)) и приравнивании ее к нулю согласно
теореме о необходимом условии экстремума функционала. В результате
получаются соотношения, позволяющие найти кривые, “подозрительные” на
наличие экстремума функционала. С помощью анализа второй вариации
функционала выводятся достаточные условия экстремума, позволяющие
сделать вывод о достижении минимума или максимума.
Теорема 2. Если на кривой y
*
(x), удовлетворяющей граничным
условиям y
*
(x
0
) = y
0
, y
*
(x
1
) = y
1
, достигается экстремум функционала в задаче
(1), то она удовлетворяет уравнению Эйлера
.0=−
′
yy
F
dx
d
F
В развернутой форме уравнение Эйлера имеет вид
.0=−+
′
+
′
′
′′′′
yyxyyyy
FFFyFy
Уравнение Эйлера представляет собой дифференциальное уравнение
второго порядка относительно неизвестной функции y(x). Общее решение
этого уравнения содержит две произвольные постоянные C
1
и C
2
, которые
должны определиться из граничных условий.
Интегральные кривые уравнения Эйлера называются экстремалями.
Только на удовлетворяющих граничным условиям экстремалях может
реализовываться экстремум.
Итак, для того чтобы применить необходимые условия экстремума в
задаче (1) надо выполнить следующие действия.
1. Найти
yyy
F
dx
d
FF
′′
,, и записать уравнение Эйлера.
2. Найти общее решение уравнения Эйлера y = y(x,C
1
,C
2
).
3. Определить постоянные C
1
и C
2
из граничных условий, решая
систему
y(x
0
, C
1
, C
2
) = y
0
,

y(x
1
, C
1
, C
2
) = y
1
.
В результате получить экстремаль y
*
(x), на которой может достигаться
экстремум функционала.
Пример 1. Найти экстремаль функционала
,)())((
1
0
22
∫
′
+= dxyyxyJ
удовлетворяющую, граничным условиям y(0) = 0, y(1) = 1.
Так как yF
dx
d
yFyFyyF
yyy
′′
=
′
==
′
+=
′′
2,2,2,
22
, то уравнение Эйлера
будет иметь вид y
′′
- y = 0. Найдем общее решение этого уравнения,
определим константы C
1
и C
2
и получим экстремаль y
*
(x).
.
1
1
)(
,
1
,
1
,1)1(
,0)0(
,)(
22
*
2
2
2
1
1
21
21
2121
21
xx
xxxx
e
e
e
e
e
e
xy
e
e
C
e
e
C
eCeCy
CCy
eCeCeCeCxy
−
−
−
−
+
−
=
−
=
−
=
=+=
=+=
+=+=
λλ
Пример 2. Найти экстремаль функционала
∫
−
′
−=
0
1
2
)12())(( dxyyxyJ
,
удовлетворяющую граничным условиям y(-1) = 1, y(0) = 0.
Так как yF
dx
d
yFxFyyF
yyy
′′
−=
′
−==
′
−=
′′
2,2,12,12
2
, то уравнение
Эйлера будет имеет вид y
′′
= -6x. Найдем общее решение этого уравнения,
определим константы C
1
и C
2
и получим экстремаль y
*
(x).
y
′
= -3x
2
+ C
1
, y = -x
3
+ C
1
x + C
2
,
y(-1) = 1 – C
1
+ C
2
= 1,
y(0) = C
2
= 0,
y
*
(x) = - x
3
.
Пример 3. Найти экстремаль функционала J(y(x))=
∫
−
2
0
2'
)(
2
π
dxyy
Удовлетворяющую граничным условиям y(0)=1, y(
2
π
)=0.
Составим уравнение Эйлера:
2'
2
yyF −=
, yF
y
2−= ,
'
2
'
yF
y
=
,
''
2
'
yF
dx
d
y
=
,
0,0
''
'
=+=− yyF
dx
d
F
y
y
Найдем общее решение уравнения Эйлера, определим константы C
1
и
C
2
0
''
=+ yy
, однородное уравнение:

y(x)=C
1·
cos(x)+C
2
·sin(x), y(0)=C
1
=1, y(
2
π
)=C
2
=0.
Получим экстремаль y
*
(x)=cos(x).
Пример 4. Найти экстремаль функционала J(y(x))=
∫
++
1
0
'2
)2(
2
dxyeyy
x
,
удовлетворяющую граничным условиям y(0)=0, y(1)=0.
Составим уравнение Эйлера
x
yeyyF 2
2
'2
++=
,
x
y
eyF 22 +=
,
'
2
'
yF
y
=
,
''
2
'
yF
dx
d
y
=
,
0222,0
''
'
=−+=− yeyF
dx
d
F
x
y
y
,
x
eyy =−
''
.
Найдем общее решение неоднородного дифференциального уравнения,
определим константы
y(x)=C
1
e
x
+C
2
e
-x
+
2
x
e
x
, y(0)=C
1
+C
2
=0, y(1)=C
1
e+C
2
e
-1
+
2
e
=0
C
1
=
)1(2
2
2
−
−
e
e
, C
2
=
)1(2
2
2
−e
e
.
Получим экстремаль
xxx
e
x
e
e
e
e
e
e
xy
2
)1(2)1(2
)(
2
2
2
2
*
+
−
+
−
−=
−
.
Найти экстремали функционалов
1. J(y(x))=
∫
1
0
'
2
dxy
, y(0)=0, y(1)=1. (отв. y
*
(x)=x )
2. J(y(x))=
∫
−
1
0
''
)(
2
dxyxy , y(0)=1, y(1)=1/4. (отв. y
*
(x)=x
2
/4-x+1 )
3. J(y(x))=
∫
+
2
1
2'2
)12(
2
dxyyx
, y(1)=1, y(2)=8. (отв. y
*
(x)=x
3
)
4. J(y(x))=
∫
−
8
4
2
)4( dxyx
, y(4)=1, y(8)=2. (отв. y
*
(x)=x/4 )
5. J(y(x))=
∫
−
4
2
''
)2(
34
dxyyxy
, y(2)=1, y(4)=5. (отв. y
*
(x)=2x-3 )
6. J(y(x))=
∫
−
2
0
''
)3(
23
dxyyxy
, y(0)=4, y(2)=6. (отв. y
*
(x)=x+4 )
7. J(y(x))=
∫
++
1
0
2''
)243(
2
dxyxyyy
, y(0)=1, y(1)=0. (отв. y
*
(x)=x
4
-2x+1 )
8. J(y(x))=
∫
++
1
0
''
)1(
2
dxyy
, y(0)=1, y(1)=2. (отв. y
*
(x)=x+1 )

9. J(y(x))=
∫
−
e
dxyxy
1
''
)2(
2
, y(1)=1, y(e)=2. (отв. y
*
(x)=ln(x)+1 )
10. J(y(x))=
∫
+
2
1
2'
)( dxyxy
, y(1)=1, y(2)=1/2. (отв. y
*
(x)=1/x )
11. J(y(x))=
∫
++
2
1
2
'
)
)ln(2
(
2
dx
x
xy
x
y
xy
, y(1)=0, y(2)=1-ln(2). (отв. y
*
(x)=
)ln()
1
(
3
2
x
x
x −− )
12. J(y(x))=
∫
++
2
1
'
3
2
)8
3
(
2
dxy
x
y
x
y
, y(1)=0, y(2)=8ln(2). (отв. y
*
(x)=x
3
ln(x) )
13. J(y(x))=
∫
+
2
1
''
)2(
2
dxyyxy
, y(1)=0, y(2)=ln(2). (отв. y
*
(x)=ln(x) )
14. J(y(x))=
∫
−
−
+
1
2
2'3
)3(
2
dxxyyx
, y(-2)=15/8, y(-1)=0. (отв. y
*
(x)= x
x
−
3
1
)
15. J(y(x))=
∫
+++
2
1
'22'
))1()(( dxyxyxy , y(1)=-1/2, y(2)=1. (отв. y
*
(x)=
x
x
2
1
2
1
−+ )
2.2. Функционалы, зависящие от нескольких функций
Рассмотрим множество M допустимых функций y
1
(x), y
2
(x),…,y
n
(x),
непрерывно дифференцируемых на отрезке [ x
0
, x
1
], удовлетворяющих
граничным условиям y
i
(x
0
) = y
i0
, y
i
(x
1
) = y
i1
.
На множестве M задан функционал
∫
′′
=
1
0
))(),...,(),(),...,(,())(),...(),((
1121
x
x
nnn
dxxyxyxyxyxFxyxyxyJ ,
где подынтегральная функция имеет непрерывные частные производные до
второго порядка включительно по всем переменным.
Среди допустимых функций требуется найти функции
)(),...,(),(
**
2
*
1
xyxyxy
n
, на которых функционал достигает экстремума.
Искомые экстремали являются решением системы дифференциальных
уравнений второго порядка, называемой системой Эйлера
.,...,2,1,0 niF
dx
d
F
ii
yy
==−
′
Эта система уравнений относительно искомых функций играет в
поставленной задаче ту же роль, что и уравнение Эйлера для одной
неизвестной функции y(x).
Итак, для того чтобы применить необходимые условия экстремума в
поставленной задаче надо выполнить следующие действия.
1. Найти niF
dx
d
FF
iii
yyy
,...,2,1,,, =
′′
и записать систему уравнений Эйлера

.,...,2,1,0 niF
dx
d
F
ii
yy
==−
′
2. Найти общее решение системы уравнений Эйлера.
3. Определить постоянные C
1
,…,C
2n
из граничных условий, решая
систему
y
i
(x
0
, C
1
,…, C
2n
) = y
i0
, i = 1,2,…,n,
y
i
(x
1
, C
1
,…, C
2n
) = y
i0
, i = 1,2,…,n.
В результате получить экстремали
)(),...,(),(
**
2
*
1
xyxyxy
n
, на которых может
достигаться экстремум функционала.
Пример 1. Найти экстремали функционала
,)126())(),((
1
0
2
2
12121
∫
++
′′
= dxyxxyyyxyxyJ
удовлетворяющие граничным условиям: y
1
(0) = y
2
(0) = 0, y
1
(1) = y
2
(1) = 2.
.,,,,12,6,126
1212
2
2
2
121
212121
yF
dx
d
yF
dx
d
yFyFxFxFyxxyyyF
yyyyyy
′′
=
′′
=
′
=
′
===++
′′
=
′′′′
Запишем систему уравнений Эйлера
012
,06
1
2
2
22
11
=
′′
−=−
=
′′
−=−
′
′
yxF
dx
d
F
yxF
dx
d
F
yy
yy
Найдем общее решение системы y
1
(x) = x
4
+C
1
x +C
2
, y
2
(x) = x
3
+C
3
x +C
4
.
Определим константы из граничных условий С
1
= С
3
= 1, С
2
= С
4
= 0,
запишем экстремали функционала y
1
*
(x) = x
4
+x, y
2
*
(x) = x
3
+x.
Пример 2. Найти экстремали функционала
∫
+
′
+
′
=
2
0
21
2
2
2
121
)2())(),((
π
dxyyyyxyxyJ ,
удовлетворяющие граничным условиям:
y
1
(0) = y
2
(0) = 0, y
1
(π/2) = 1, y
2
(π/2) = -1.
21211221
2
2
2
1
2,2,2,2,2,2,2
212121
yF
dx
d
yF
dx
d
yFyFyFyFyyyyF
yyyyyy
′′
=
′′
=
′
=
′
===+
′
+
′
=
′′′′
Запишем систему уравнений Эйлера
022
,022
21
12
22
11
=
′′
−=−
=
′′
−=−
′
′
yyF
dx
d
F
yyF
dx
d
F
yy
yy
Решаем систему, сводя ее к одному уравнению относительно
переменной y
1
, y
1
′′′
= y
2
′
, y
1
(4)
= y
2
′′
, y
1
(4)
– y
1
= 0. Общее решение полученного
однородного уравнения записывается в форме y
1
(x) = C
1
e
x
+ C
2
e
-x
+C
3
cosx +
C
4
sinx, тогда y
2
(x) = C
1
e
x
+ C
2
e
-x
- C
3
cosx - C
4
sinx.
Определяем постоянные С
1
, С
2
, С
3
, С
4
из граничных условий
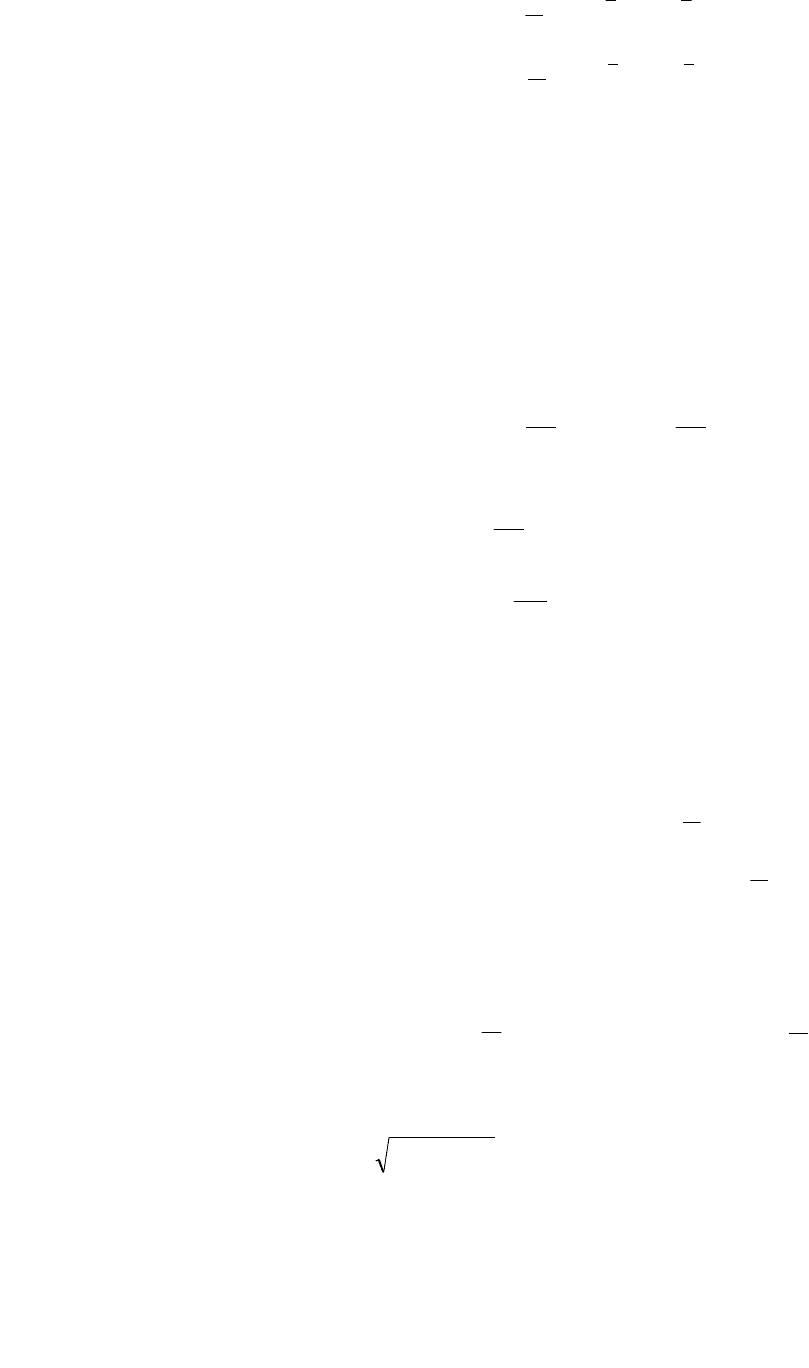
.1)
2
(
,1)
2
(
,0)0(
,0)0(
4
2
2
2
12
4
2
2
2
11
3212
3211
−=−+=
=++=
=−+=
=
+
+
=
−
−
CeCeCy
CeCeCy
CCCy
CCCy
ππ
ππ
π
π
Имеем: С
1
=С
2
=С
3
=0, С
4
= 1. Записываем экстремали:
y
1
*
(x) = sinx, y
2
*
(x) = -sinx.
Пример 3. Найти экстремали функционалов
J(y
1
(x),y
2
(x))=
∫
−+−
π
0
'
221
2
1
'
1
)22(
22
dxyyyyy
Удовлетворяющие граничным условиям y
1
(0)=y
2
(0)=0, y
1
(π)=y
2
(π)=1.
22
'
221
2
1
'
1
22 yyyyyF −+−=
,
21
24
1
yyF
y
+−=
,
1
2
2
yF
y
=
,
'
1
2
'
1
yF
y
=
,
'
2
2
'
2
yF
y
−=
,
''
1
2
'
1
yF
dx
d
y
=
,
''
2
2
'
2
yF
dx
d
y
−=
.
Запишем систему уравнений Эйлера
02,0
21
''
1
'
1
1
=−+=− yyyF
dx
d
F
y
y
0,0
1
''
2
'
2
2
=+=− yyF
dx
d
F
y
y
.
Решаем систему, сводя ее к одному уравнению относительно
переменной y
1
, 02
1
''
1
)4(
1
=++ yyy .
Общее решение полученного однородного уравнения записывается в
виде:
y
1
(x)=C
1
·cos(x)+C
2
·sin(x)+x(C
3
·cos(x)+C
4
·sin(x))
В силу граничных условий C
1
=0, C
3
=
π
1
− тогда
y
2
(x)=C
2
·sin(x)+C
4
·(2cos(x)+x·sin(x))+
π
1
(2·sin(x)-x·cos(x))
Постоянные С
2
и С
4
находим, используя граничные условия для y
2
(x) ,
то есть C4=0, C2 –произвольно.
Запишем экстремали
)cos()()sin()(
2
*
1
x
x
xCxy
π
−=
,
))cos()sin(2(
1
)sin()(
2
*
2
xxxxCxy −+=
π
.
Найти экстремали функционалов, зависящих от нескольких функций.
1. J(y
1
,y
2
)=
∫
++
3
0
'
2
'
1
22
1 dxyy , y
1
(0)=1, y
2
(0)=-2, y
1
(3)=7, y
2
(3)=1
Отв.
−=
+=
2)(
12)(
*
2
*
1
xxy
xxy
.
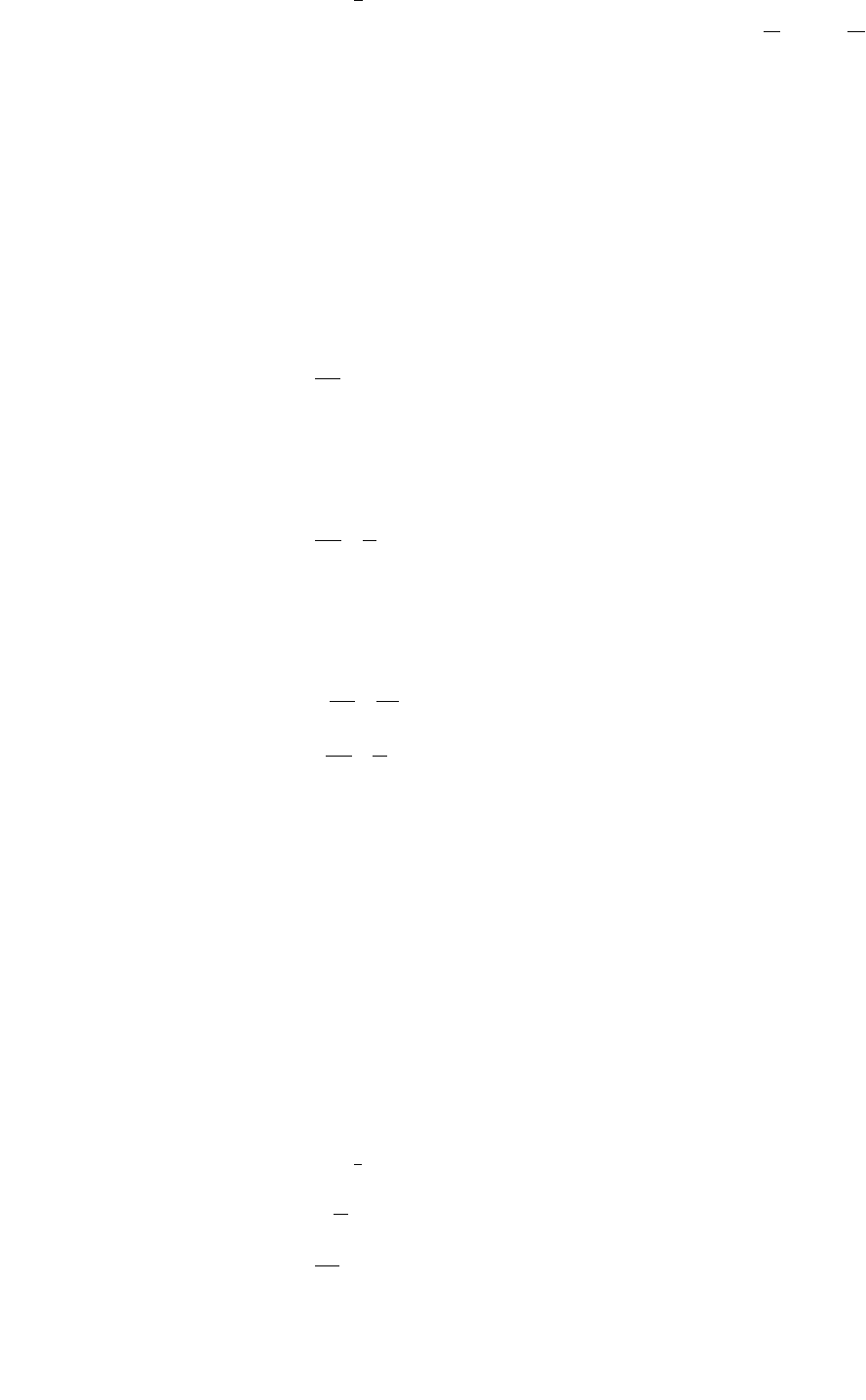
2. J(y
1
,y
2
)=
∫
−+
2
0
21
'
2
'
1
)2(
22
π
dxyyyy , y
1
(0)= y
2
(0)=0, y
1
(
2
π
)= y
2
(
2
π
)=1
Отв.
=
=
)sin()(
)sin()(
*
2
*
1
xxy
xxy
.
3. J(y
1
,y
2
)=
∫
++
1
0
2
2
1
'
2
'
1
)126( dxyxxyyy
, y
1
(0)= y
2
(0)=0, y
1
(1)= y
2
(1)=1
Отв.
=
=
3*
2
4*
1
)(
)(
xxy
xxy
.
4. J(y
1
,y
2
)=
∫
++
1
0
1
'
2
'
1
)2(
22
dxyyy , y
1
(0)= y
2
(0)=1, y
1
(1)=3/2, y
2
(1)=1
Отв.
=
+=
1)(
1
2
)(
*
2
2
*
1
xy
x
xy
.
5. J(y
1
,y
2
)=
∫
−++
1
0
21
'
2
'
1
)422(
22
dxyyyy , y
1
(0)= y
2
(0)=0, y
1
(1)=1, y
2
(1)=2
Отв.
+−=
+=
xxxy
x
x
xy
3)(
4
3
4
)(
2*
2
2
*
1
.
6. J(y
1
,y
2
)=
∫
+−
1
0
1
2
2
'
2
'
1
)3( dxyxxyyy , y
1
(0)= y
2
(0)=0, y
1
(1)=2, y
2
(1)=-1
Отв.
−=
+−=
x
x
xy
x
x
xy
4
5
4
)(
6
13
6
)(
4
*
2
3
*
1
.
7. J(y
1
,y
2
)=
∫
+++
2
1
'
12
'
21
'
2
'
1
)22(
22
dxyyyyyy
, y
1
(1)=2, y
2
(1)=4, y
1
(2)=5, y
2
(2)=10
Отв.
−=
−=
26)(
13)(
*
2
*
1
xxy
xxy
.
8. J(y
1
,y
2
,y
3
)=
dxyyyyyyyxy
∫
+++++
2
1
'
23
'
3
'
32
'
2
'
11
)2212(
222
, y
1
(1)=0, y
2
(1)=2,
y
3
(1)=0, y
1
(2)=6, y
2
(2)=3, y
3
(2)=2. Отв.
−=
+=
−=
22
1
1
*
3
*
2
3*
1
xy
xy
xy
.
9. J(y
1
,y
2
)=
∫
−
1
2
1
'
21
'
1
)2(
2
dxyxyy , y
1
(1/2)=2, y
2
(1/2)=15, y
1
(1)=y
2
(1)=1
Отв.
−=
=
1
2
)(
1
)(
3
*
2
*
1
x
xy
x
xy
.
