Семенкин Е.С. Методы оптимизации. Практикум
Подождите немного. Документ загружается.

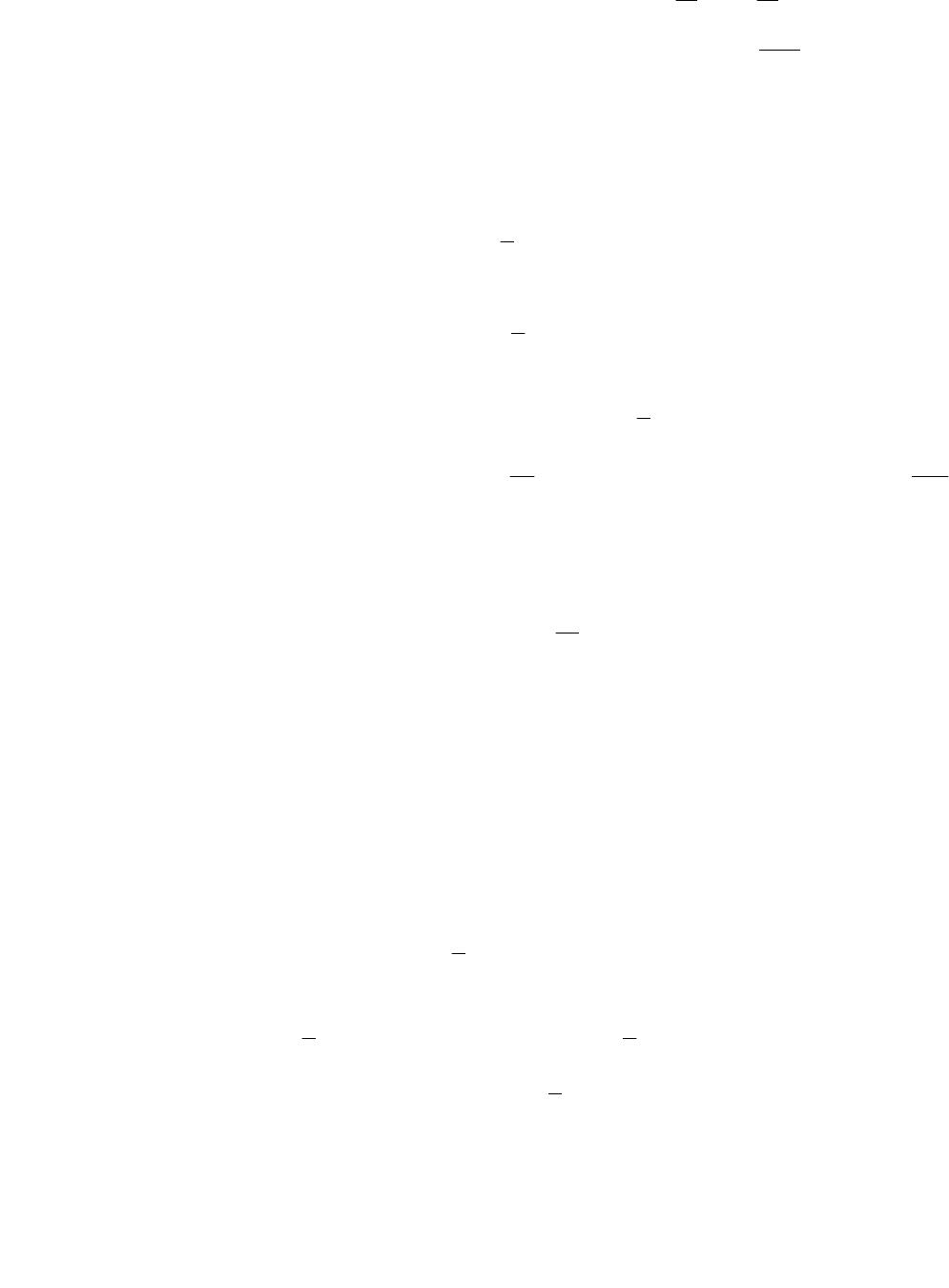
6. )(tux =
•
, x(0)=2, -1
≤
u
≤
0, J=
min)2(
2
0
2
→+
∫
dtxu
,
ответ
[
]
−=
∈+−=
1
3,0,2
*
*
u
ttx
и
[ ]
−
=
∈+−=
2
2
4,3,
2
13
4
2
*
2
*
t
u
tt
t
x
2.3. Задачи с подвижными концами
Пример 1. Даны модель объекта управления )()( tutx =
•
, x(0)=1, x∈R,
u∈R, t∈[0, t
1
] и функционал J=
min)(4
2
1
1
0
2
1
→+
∫
txdtu
t
. Задано конечное условие
x(t
1
)=t
1
-1. Найти оптимальную тройку t
1
, x
*
(t), u
*
(t).
В этом примере f
0
(t, x, u)=
2
2
1
u , f(t, x, u)=u, F(t
1
, x)=4x и задано
граничное условие Г(t
1
, x(t
1
))=t
1
-x(t
1
)-1=0. Решается задача Больца.
Составляем гамильтониан H (t, Ψ, x, u)=Ψu-
2
2
1
u
. Находим максимум
гамильтониана по управлению:
u
∂
∂
H (t, Ψ, x, u)=Ψ(t)-u=0, u
*
(t)=Ψ(t),
2
2
du
∂
H
(t, Ψ, x, u)=-1<0. Необходимое и достаточное условия максимума выполнены.
Выписываем канонические уравнения принципа максимума:
),()()(
*
ttutx ψ==
•
x(0)=1,
x
t
∂
∂
−=
•
)(ψ H (t, Ψ, x, u)=0.
Для нахождения еще одного краевого условия и определения t
1
*
,
рассмотрим условие трансверсальности и заданное граничное условие
Г(t
1
, x(t
1
))=t
1
-x(t
1
)-1=0.
Условие трансверсальности
δF(t
1
*
)-H(t
1
*
)δt
1
+
∑
=
=
n
j
jj
xt
1
*
1
0)( δψ
выполняется для любых δt
1
, δx
j
, удолетворяющих системе δГ(t
1
*
, x
*
(t
1
*
))=0,
Г(t
1
*
, x
*
(t
1
*
))=0. Имеем δF=4δx, δГ(t
1
, x(t
1
))=δt
1
-δx=0. Тогда
4δx-H(t
1
)δt
1
+Ψ(t
1
)δx=0, δt
1
- δx=0, t
1
-x(t
1
)-1=0,
где H (t
1
, Ψ(t
1
), x(t
1
), u
*
(t
1
))
2
1
=Ψ
2
(t
1
). Поскольку t
1
не фиксировано, то 0
1
≠tδ ,
из вариации граничных условий получим δt
1
=δx. Итак для любых δx,
получим: (4- )()(
2
1
11
2
tt ψψ + )δx=0, отсюда 4- )()(
2
1
11
2
tt ψψ + =0. Решаем краевую
задачу )()( ttx ψ=
•
, x(0)=1, 0)( =
•
tψ , 4- )()(
2
1
11
2
tt ψψ + =0, t
1
-x(t
1
)-1=0.
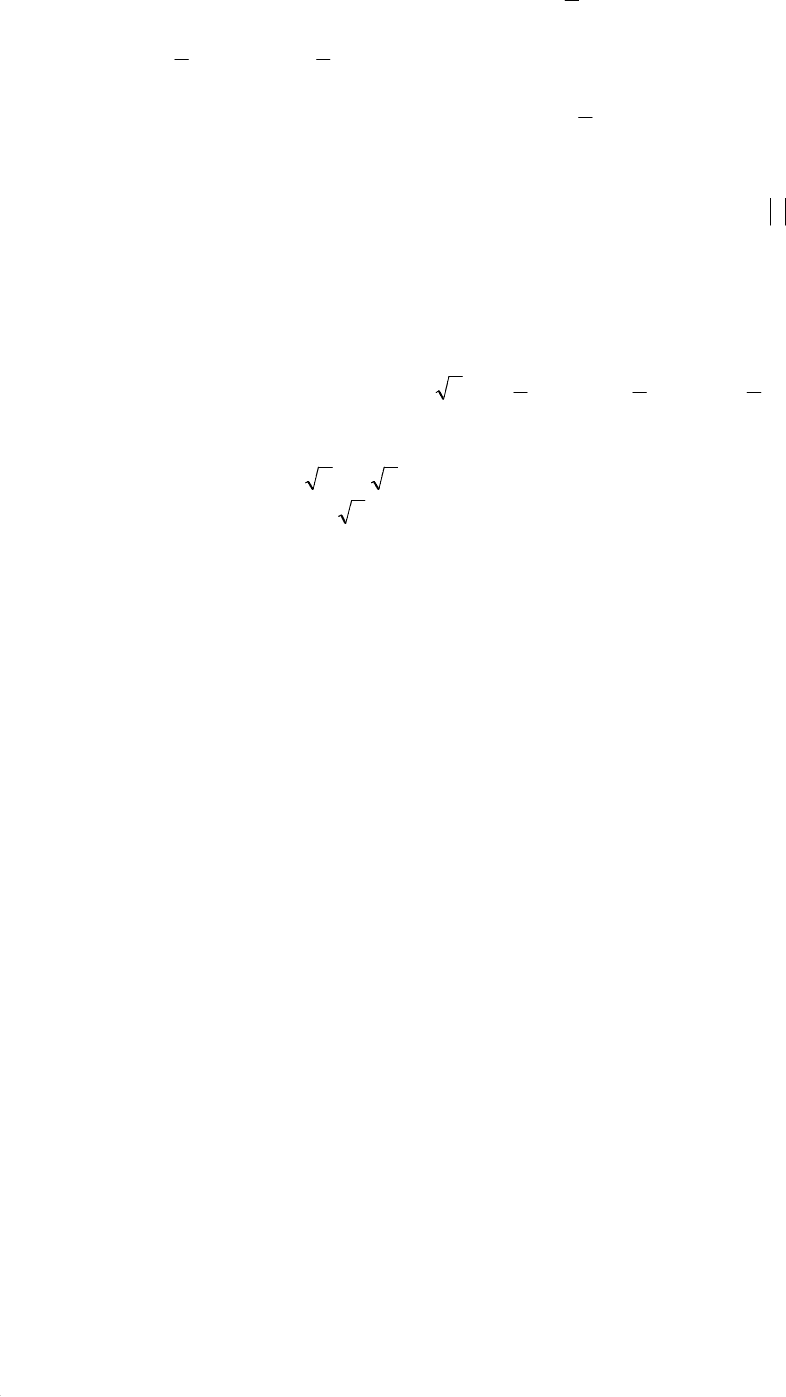
Получим Ψ(t)=const=C, x(t)=Ct+1. Для определения постоянной C при
t=t
1
решаем систему уравнений: 4- CC +
2
2
1
=0, t
1
-Ct
1
-2=0. Получим C=-2, t
1
=
3
2
; C=4, t
1
=-
3
2
. Второе решение не подходит, так как при t
1
должно быть
положительным. Окончательно t
1
*
=
3
2
, x
*
(t)=-2t+1, u
*
(t)=-2.
Найти оптимальное управление.
1.
2
1
xx =
•
, 4
2
=
•
x , x
1
(0)+x
1
(1)=0, x
2
(0)+x
2
(1)=0, 2≤u , J= min)(
1
0
1
→
∫
dttx ,
ответ
−=
−=
=
12
1
2
*
2
2*
1
*
tx
tx
u
.
2. )(tux =
•
, x(0)= 23 , J= min)(
2
1
)2(
2
1
)(
2
1
1
22
1
0
2
1
→+−+
∫
txtdttu
t
,
ответ
−=
+−=
=
2
232
2
*
*
*
1
u
tx
t
.

Глава 6. Применение принципа Беллмана
Рассмотрим некоторую динамическую систему S.
Пусть на k-м шаге (k = 1, 2,..., n) состояние системы
определяется совокупностью чисел X
k
=(
x x x
k
k
m
k
1
2
, ,...,
), которые
получены в результате реализации управления _U
k
,
обеспечивающего переход системы S из состояния X
1−k
в состояние
X
k
. Будем полагать, что X
k
зависит от X
1−k
и U
k,
и не зависит от
того, как система пришла в состояние X
1−k
(свойство отсутствия
последействия).
Пусть W
k
(X
1−k
, U
k
) есть доход (выигрыш), полученный в
результате реализации k-го шага. Тогда общий выигрыш полагаем
равным F =
∑
=
n
k 1
W
k
(X
1−k
, U
k
) (свойство аддитивности целевой
функции).
Совокупность управлений U
*
= (
*
1
u,
*
2
u ,...,
*
n
u ), в результате
реализации которых система S переходит за n шагов из начального
состояния X
0
в конечное X
n
и при этом функция F принимает
наибольшее значение, будем называть оптимальной стратегией
управления.
Принцип оптимальности Белмана.
Каково бы ни было состояние системы перед очередным
шагом, надо выбрать управление на этом шаге так, чтобы выигрыш
на данном шаге плюс оптимальный выигрыш на всех последующих
шагах был бы максимальным.
Оптимальную стратегию можно получить, если сначала найти
оптимальную стратегию управления на последнем n-м шаге, затем
на двух последних шагах и т.д. вплоть до первого шага. Таким
образом, решение задачи динамического программирования
целесообразно начинать с определения оптимального решения на
последнем n-м шаге. Для того, чтобы найти это решение, нужно
сделать всевозможные предположения о том, как мог закончиться
предпоследний шаг и с учетом этого выбрать управление
0
n
u ,
обеспечивающее максимальное значение функции W
n
(X
1−n
, U
n
).
Такое управление
0
n
u
, выбранное при определенных
предположениях о том, как окончился предыдущий этап,
называется условно оптимальным.
Принцип оптимальности Беллмана требует находить на
каждом шаге условно оптимальные управления для любого из
возможных исходов предыдущего шага.
Обозначим через F
n
(X
0
) максимальный доход, получаемый за
n шагов при переходе системы S из начального состояния X
0
в

конечное состояние X
n
, а через F
n-k
(X
k
) - то же при переходе из
X
k
в X
n
и оптимальном управлении на последних n-k шагах.
Тогда
F
n
(X
0
) =
k
max
u
[W
1
(X
0
, U
1
) + W
2
(X
1
, U
2
) +... + W
n
(X
1−n
, U
n
)],
F
n-k
(X
0
) =
1+k
max
u
[W
k+1
(X
k
, U
k+1
) + F
n-k-1
(X
1+k
)],
.1,0 −= nk
Последнее соотношение называется основным
функциональным уравнением Беллмана и представляет собой
математическую формулировку принципа оптимальности.
Положим k = n - 1, тогда
F
1
(X
1−n
) =
n
max
u
[W
n
(X
1−n
, U
n
) + F
0
(X
n
)], (*)
где F
0
(X
n
) считаем известным.
Используя (*) и рассматривая всевозможные допустимые
состояния X
1
1
−n
, X
1
2
−n
,..., X
1−n
l
,..., системы на (n-1)-м шаге находим
условно-оптимальные управления
0
n
u
(X
1
1
−n
),
0
n
u
(X
1
2
−n
),...,
0
n
u
(X
1−n
l
),... и
соответствующие значения функции (*):
0
1
F
(X
1
1
−n
),
0
1
F
(X
1
2
−n
),...,
0
1
F
(X
1−n
l
),....
Таким образом, на n-м шаге находим условно-оптимальное
управление при любом допустимом состоянии системы после (n-
1)-го шага. То есть, в каком бы состоянии система не оказалась
после (n+1)-го шага, нам уже известно, какое следует принять
решение на n-м шаге. Известно и соответствующее значение
функции. (*)
Переходим к рассмотрению функционального уравнения при
k=n-2.
F
2
(X
2−n
) =
max
u
n-1
[W
n-1
(X
2−n
, U
n-1
) + F
1
(X
1−n
)]. (**)
Для того, чтобы найти значение F
2
для всех допустимых
значений X
2−n
, очевидно, необходимо знать W
n-1
(X
2−n
, U
n-1
) и
F
1
(X
1−n
). Но F
1
(X
1−n
) мы уже определили на предыдущем шаге.
Поэтому нужно произвести вычисления для W
n-1
(X
2−n
, U
n-1
) при
некотором наборе допустимых значений X
2−n
и соответствующих
управлений U
n-2
. Эти вычисления позволят определить условно
оптимальное управление U
n
-
1
0
для каждого X
2−n
. Каждое из таких
управлений совместно с уже выбранным управлением на
последнем шаге обеспечивает максимальное значение дохода на
двух последних шагах.
Последовательно осуществляя этот итерационный процесс,
дойдем, наконец, до первого шага. На этом шаге нам известно, в
каком состоянии может находиться система. Поэтому уже не
требуется делать предположения о допустимых состояниях

системы, а остается лишь только выбрать управление, которое
является наилучшим с учетом условно оптимальных управлений,
уже принятых на всех последующих шагах.
Таким образом, в результате последовательного прохождения
всех этапов от конца к началу определяем максимальное значение
выигрыша за n шагов и для каждого из них находим условно
оптимальное управление.
Чтобы найти оптимальную стратегию управления, то есть
определить искомое решение задачи, нужно теперь пройти всю
последовательность шагов, только на этот раз от начала к концу, а
именно: на первом шаге в качестве оптимального управления
*
1
u
возьмем найденное условно оптимальное управление U
1
0
. На
втором шаге найдем состояние X
1
*
, в которое переводит систему
управление
*
1
u
. Это состояние определяет условно оптимальное
управление U
2
0
(X
1
*
), которое теперь будем считать оптимальным (
*
2
u
). Зная
*
2
u
, находим X
3
*
=
*
2
u
(X
2
*
), а значит - определяем
*
3
u
= U
3
0
(X
3
*
), и т.д. В результате находим решение задачи - максимально
возможный доход и оптимальную стратегию управления U
*
,
включающую оптимальные управления на отдельных шагах (
*
1
u ,
*
2
u
,...,
*
n
u
).
Таким образом, мы рассмотрели нахождение решения задачи
динамического программирования в общем виде. Этот процесс
является довольно громоздким, поэтому он используется обычно с
применением ЭВМ. Отметим также, что изложена только идея,
которая должна быть реализована в том или ином виде для
каждого частного случая и далеко не всегда очевидно, как это
сделать.
Существуют реализации идей динамического
программирования для задач распределения ограниченных
ресурсов, оптимизации путей на сетях, упаковки ранца и др.,
которые могут быть использованы, если математическая
постановка решаемой задачи будет сведена к одной указанных
формулировок.
1. Задача о ранце
Задача получила такое название по аналогии с задачей
туриста, решающего, что именно взять с собой в дорогу с учетом
ограничения по весу ранца. Задача формализуется в виде задачи
целочисленного линейного программирования, где
коэффициентами целевой функции будут оценки важности

выбираемых предметов, коэффициентами ограничения - веса
предметов, свободным членом ограничения - вместительность
ранца (то есть “грузоподъемность” туриста). Переменные - это
количество предметов одного типа, укладываемых в ранец.
Например, частным случаем задачи о ранце является так
называемая одномерная задача о ранце, которая обычно
формулируется в виде
j
n
=
∑
1
c
j
x
j
→ max,
j
n
=
∑
1
a
j
x
j
≤ b,
x
i
∈ {0,1}, j = 1,..., n.
Примером реальной задачи такого типа является следующая
задача: Имеется n проектов, стоимость j-го проекта есть a
j
, его
ценность равна c
j
, j = 1,..., n. Имеется также бюджет b для
финансирования этих проектов. Задача состоит в выборе
подмножества проектов так, чтобы максимизировать суммарную
ценность, но при этом не превысить бюджет.
Главная идея динамического программирования состоит в
сведении решения сложной задачи к последовательности более
простых задач, например задачи с многими переменными к
последовательности одномерных задач.
В связи с этим мы должны выполнить две операции:
1. Погрузить данную задачу в семейство задач того же типа.
Для задачи о ранце рассматривают, например, семейство из
n(b+1) задач вида
F
i
(E) = max
j
n
=
∑
1
c
j
x
j
,
j
n
=
∑
1
a
j
x
j
≤ b - E,
x
j
∈{1,0}, j = 1,..., n,
где i изменяется от 1 до n, а Е - это целое число, изменяющееся от
0 до b.
Число Е, с помощью которого параметризуется данное
семейство задач, обычно называется переменной состояния.
Отметим, что это число приписывается ограничениям задачи.
Множество Г = {0, 1,..., b} возможных значений числа Е
называется пространством состояний задачи.
Исходная задача о ранце является членом построенного
семейства задач при i=1 и Е=0. Таким образом, мы имеет
F*=F
1
(0).

Кроме того, договоримся полагать F
i
(E) = - ∞ при Е < 0 или
когда при некотором i задача не имеет решения (например, когда Е
> b).
2. Найти рекуррентное соотношение, соединяющее
оптимальные решения различных задач семейства. В нашем случае
мы можем легко получить рекуррентное соотношение в виде
F
i
(E) =
max
x
i
=∨01
{c
i
x
i
+ F
i+1
(E+a
i
x
i
)} = max {F
i+1
(E);
c
i
+F
i+1
(E+a
i
)}.
Таким образом, для всех значений Е (0 ≤ Е ≤ b) задача
получения решения F
i
(E) из решения F
i+1
(E) упрощается до
элементарной оптимизационной задачи. Полученное рекуррентное
соотношение позволяет решить исходную задачу с помощью
алгоритма, состоящего из n шагов.
Алгоритм (динамического программирования для задачи о
ранце).
(а) Старт (шаг n)
∀ E (0 ≤ E ≤ b) вычислить F
n
(E) по формуле
F
n
(E) =
≤≤
≥≤
≥
.0– Џ - для ,0
,0 Џ - для ,
, - для ,0
nn
nnn
n
abE
cabEc
abE
(б) Шаг i.
Для i = n-1, n-2,..., 2 последовательно вычислять
∀ E (0 ≤ E ≤ b):
F
i
(E) = max {F
i+1
(E); c
i
+F
i+1
(E+a
i
)}.
(в) Шаг 1. Вычислить F* по формуле
F
*
= F
1
(0) = max {F
2
(0); c
1
+F
2
(a
1
)}.
Приведенный алгоритм, при небольших дополнительных
затратах, дает не только решение исходной задачи, но и всех
задач, отличающихся от исходной значениями свободного члена
ограничений.
Относительно этого алгоритма существует следующее общее
заключение: сложность вычислительного процесса и требуемая
память компьютера самым существенным образом зависит от b.
Это сильно ограничивает применимость метода динамического
программирования в практических задачах.
2. Простейшие задачи решаемые методом динамического
программирования
2.1. Задача о минимизации расхода горючего самолетом при наборе
высоты и скорости. Постановка задачи
Пусть самолет, находящийся на высоте Н
0
и имеющий скорость V
0
должен подняться на высоту Н
k
н иметь скорость V
k
.
Известен расход горючего при подъеме самолета с любой высоты H
1
на
любую высоту Н
2
>Н
1
при постоянной скорости, а также расход горючего при
увеличении скорости от любого значения V
1
до любого значения V
2
>V
1
при
неизменной высоте [14].
Найти оптимальное управление набором высоты и скорости, при
котором общий расход горючего минимален.
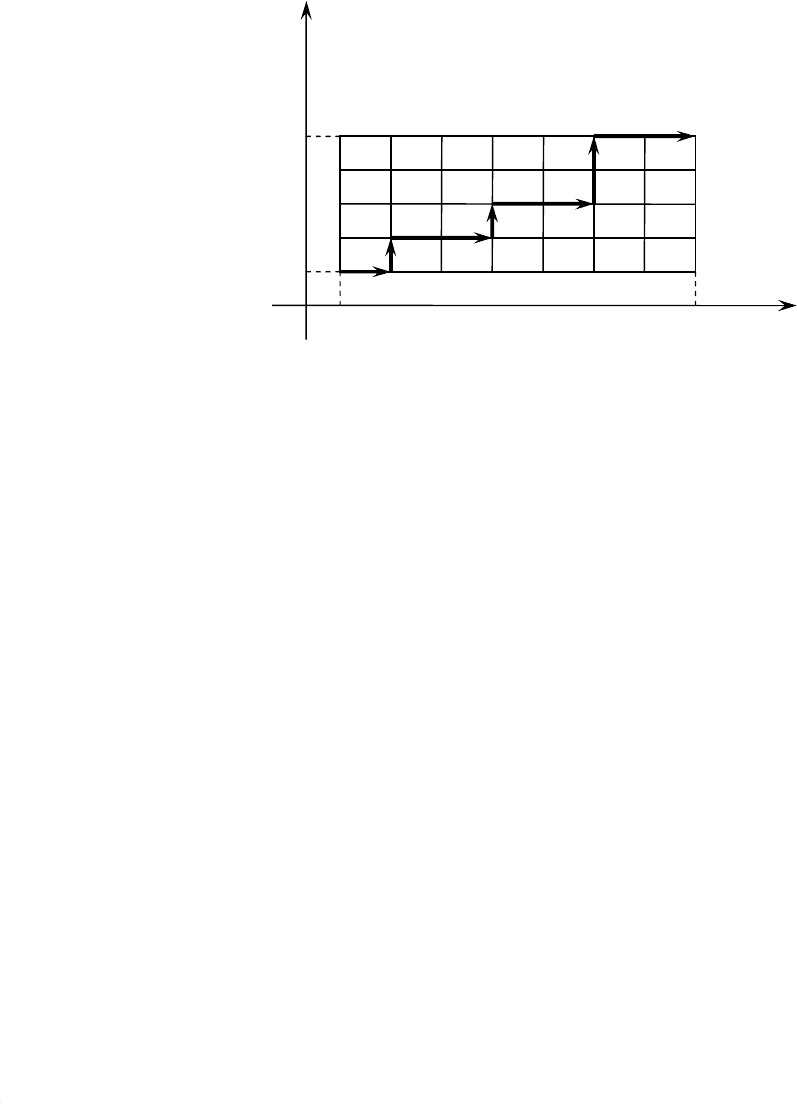
Решение. Прямоугольник ограниченный прямыми V=V
0
, V=V
k
и
Н=Н
0
, Н=H
k
является областью допустимых состояний. Начальное S
0
(V
0
, Н
0
)
и конечное S
k
(V
k
, H
k
) состояния вполне определены, как две точки S
0
и S
k
на
плоскости.
Чтобы построить решение методом динамического программирования,
разобьем отрезок (H
k
-Н
0
) на n
1
, а отрезок (V
k
-V
0
) - на п
2
равных частей
(этапов).
Пусть за один шаг самолет может увеличить либо высоту на величину
∆H=(H
k
-Н
0
)/n
1
, либо скорость на величину ∆V=(V
k
-V
0
)/n
2.
Очевидно,
существует множество траекторий (управлений), представляющих собой
ломаные линии, по которым точка S может переместиться из S
0
в S
k
.
Решение задачи состоит в том, чтобы из множества управлений
выбрать такое, которое позволит минимизировать расход горючего W,
равный сумме расходов горючего на каждом этапе соответствующей
ломаной линии.
0
H
K
H
0
S
K
V
V
0
H
K
S

Расчеты начинаем из верхней правой точки. Точки пересечения линий
разбиения изображают кружками, в которые записывают расход горючего.
Оптимизацию начинаем с последнего шага. Рассмотрим отдельно
правый верхний угол прямоугольной сетки с конечной точкой S
k
. В точку S
k
можно прийти либо из точки A
1
, либо из A
2
Условно оптимальные управления, отмечаем стрелкой, выходящей из
кружка и указывающей, как управлять самолетом на последнем шаге, если в
результате предыдущего шага он окажется в одном из рассмотренных
состояний. Таким образом, последний шаг спланирован, поскольку найдены
условно оптимальные управления для предполагаемых состояний системы на
(п-1)-м шаге и известны значения функции W для каждого из этих состояний.
Переходим к планированию предыдущего (n-1) шага. Чтобы выбрать
условно оптимальные управления на этом шаге, нужно рассмотреть
возможные состояния, в которые может прийти система на (n-2) шаге.
На (n-2) шаге состоянию самолета может соответствовать одна из трех
точек: B
1
, B
2
или В
3
. Найдем условно оптимальное управление для этих
состояний и соответствующий этому управлению минимальный расход
горючего. Продолжая процесс для оставшихся шагов, приходим в точку S
0
.
Выбирая для этого состояния уже не условно оптимальное, а оптимальное
управление, получаем оптимальное управление для всего процесса.
2. 2. Задача определения кратчайших расстояний по заданной сети
Анализируя окончательные решения предыдущей задачи, можно
сделать вывод, что найдены оптимальные управления не только для случая,
когда состояние системы характеризуется точкой S
0
, но и для случая, когда
оно определяется любой другой узловой точкой.
Полученное свойство можно использовать для решения задачи, по
отысканию кратчайших расстояний от каждой точки до любой другой по
некоторой сети.
Эта задача нашла широкое применение для определения значений
стоимости С
ij
(i - номер поставщика, j - номер потребителя), которые входят в
критерий оптимальности при решении транспортной задачи линейного
программирования.
Решение задачи по определению кратчайших расстояний между
поставщиками и потребителями по существующей транспортной сети
является исходным этапом при решении таких экономических задач:
- оптимальное закрепление потребителей за поставщиками,
- повышение производительности транспорта за счет сокращения
непроизводительного пробега и др.

Пусть на некоторой поверхности взято конечное число точек P
1
, P
2
,...,
P
i
,..., P
j
,..., P
n
, соединенных всевозможными непересекающимися отрезками
линий (P
i
,P
j
), называемых звеньями или связями. Тогда совокупность точек и
их связей называется сетью.
Сеть называется достаточно связанной, если существует путь,
состоящий из звеньев и соединяющий любые две точки сети из точек P
1
,
P
2
,..., P
n
.
Постановка задачи. Пусть задана достаточно связанная сеть, на
которой каждому звену (P
i
,P
j
) поставлено в соответствие некоторое
действительное неотрицательное число l
ij
- его длина.
Необходимо определить кратчайшие расстояния по сети от каждой
точки до всех остальных и соответствующие пути, по которым они проходят.
Пронумеруем точки сети в любом
порядке (слева направо, сверху вниз) и
укажем длину каждого звена.
Две точки назовем соседними, если
они непосредственно соединены связью.
Положим, что l
ij
=l
ji
,
Необходимо найти кратчайшие
расстояния по сети от каждой точки до всех
остальных.
Разобьем процесс на п этапов, а каждый этап - на п-1 шагов.
Этап заключается в отыскании кратчайших расстояний и маршрутов,
по которым они проходят, от какой-нибудь одной точки, заранее
зафиксированной, до всех остальных.
Шаг состоит в отыскании кратчайшего расстояния от фиксированной
точки до каждой из остальных через соседние, кратчайшие расстояния до
которых уже определены.
Для решения задачи используем метод динамического
программирования и отыскиваем кратчайшие расстояния не от
фиксированной точки до всех остальных, а расстояние от всех остальных
точек до фиксированной через соседние точки. Связь, через которую
проходит кратчайшее расстояние, после каждого шага отмечаем стрелкой.
Для удобства точки сети обозначим кружками.
Алгоритм решения задачи.
1. Фиксируем точку Р
i
, до которой необходимо рассчитать кратчайшее
расстояние от всех остальных.
В кружке, обозначающем эту точку, записываем нуль, так как
расстояние от точки P
i
до нее самой равно нулю.
