Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

934 Appendix B Trigonometry

B.2.5 Integration



sin udu=−cos u + C



cos udu= sin u + C



tan udu= ln

sec u

+ C



cot udu=−ln

sin u

+ C



sec udu= ln

sec u + tan u

+ C

= ln



tan



π +





+ C



csc udu= ln

csc u − cot u

+ C

= ln



tan



+ C

B.3 Trigonometric Identities and Laws

Consider Figure B.4, and apply the Pythagorean Theorem. The following relationship

holds:

+ y

= r

If we apply a little arithmetic manipulation and the deﬁnitions of the sin and cos

functions, we get

+ y

= r

+ y

= 1 Dividing both sides by r

sin

θ + cos

θ = 1 Using the deﬁnition of sin and cos

B.3 Trigonometric Identities and Laws 935

The next set of fundamental identities involves the negation of an angle. Consider

an angle θ and the deﬁnitions found in Section B.2.1. If we consider an angle −θ,we

can see that the terminal side of such an angle intercepts the unit circle at the same

x-coordinate as does the terminal side of θ , but the y-coordinate is negated (observe

Figure B.5). We can then, using the deﬁnitions given in Section B.2.1, deﬁne

sin (−θ) =

−y

=−

=−sin θ

and

cos (−θ) =

= cos θ

and

tan(−θ) =

−y

=−

=−tan(θ)

B.3.1 Periodicity

The graphs of the trigonometric functions shown in Figure B.7 make it appear that

the trigonometric functions are periodic, and inspection of the deﬁnitions given in

Section B.2.1 reveals that the trigonometric function values for all angles sharing a

common terminal side are the same. Thus, it is true by deﬁnition and the observation

that a circle comprises 2π radians that

sin θ = sin(θ ± 2nπ)

cos θ = cos(θ ± 2nπ)

csc θ = csc(θ ± 2nπ)

sec θ = sec(θ ± 2nπ)

936 Appendix B Trigonometry

for all n = ..., −2, −1, 0, 1, 2, .... However, the tangent and cotangent functions

haveaperiodofπ :

tan θ = tan(θ ± nπ)

cot θ = cot(θ ± nπ)

for all n = ..., −2, −1, 0, 1, 2, ....

B.3.2 Laws

This section discusses three laws that deﬁne relationships between general triangles’

edges, angles, and trigonometric functions.

Law of Sines

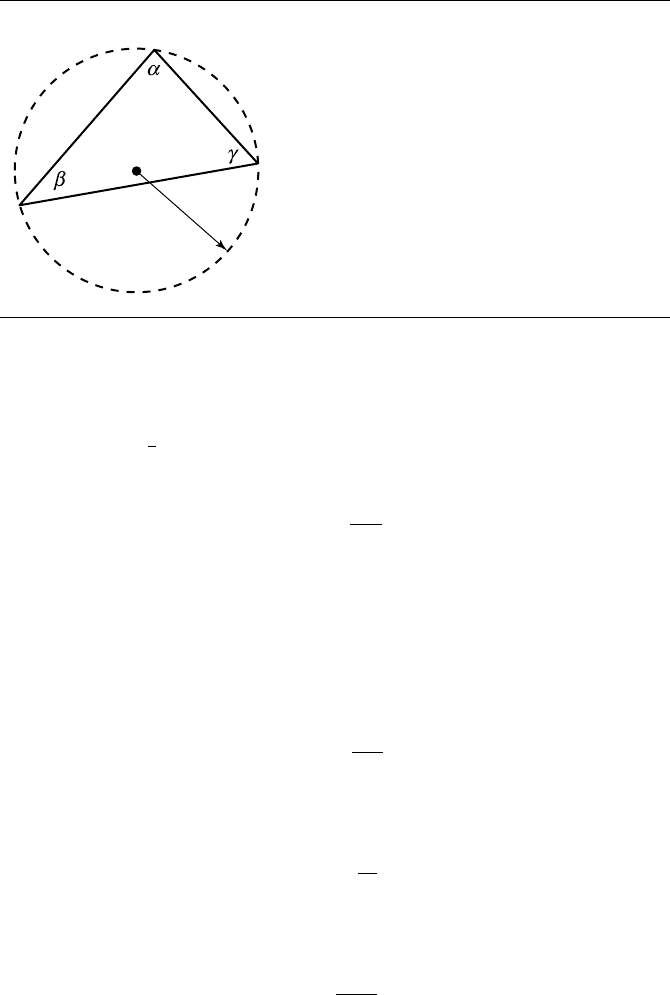
The law of sines is one of the fundamental trigonometric relationships, and it relates

to general triangles, not only right triangles (see Figure B.8). Informally put, the law

of sines states that for any triangle, the ratios of each side to the angle opposite are all

equal

sin α

sin β

sin γ

= 2r

where r is the circumradius (the radius of the circle passing through the triangle’s

vertices).

The following proof is due to Ronald Goldman (1987):

2Area(ABC) =(A − B) × (C − B)=ca sin β

2Area(BCA) =(B − C) × (A − C)=ab sin γ

2Area(CAB) =(C − A) × (B − A)=bc sin α

∴ ca sin β = ab sin γ = bc sin α

∴

sin α

sin β

sin γ

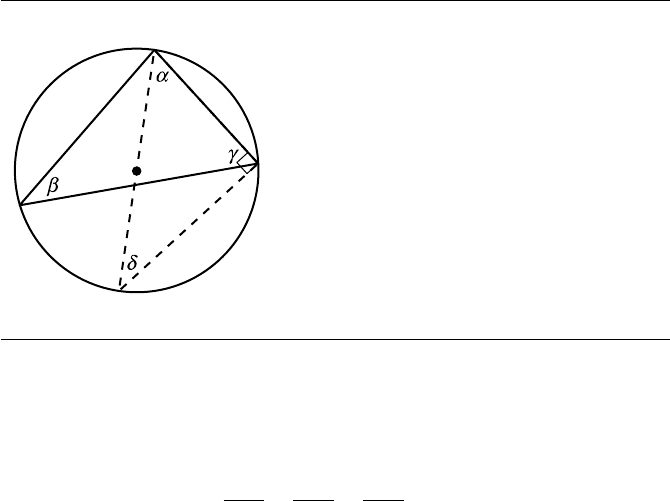
The relationship to the circumradius can also be easily proved. Consider again

our triangle ABC; choose any vertex, and draw a line from it, through the circum-

center (the center of the circle that passes through a triangle’s vertices), and intersect-

ing the circle at a point D (Figure B.9).

B.3 Trigonometric Identities and Laws 937

Figure B.8

The law of sines.

We know that



ADC is a right angle because it subtends a semicircle. By deﬁni-

tion of the sine function, we then have

sin δ =

But of course δ = β because they both subtend the same arc



AC. Thus,

sin δ = sin β

Substituting, we get

sin β =

But since AD passes through the circumcenter, AD =2r, and so we have

sin β =

Rearranging, we have

2r =

sin β

938 Appendix B Trigonometry

Figure B.9 Proof of the law of sines.

Combined with the previous proof, we can then conclude

sin α

sin β

sin γ

= 2r

The Law of Cosines

The law of cosines is another frequently useful relationship and may be viewed as a

generalization of the Pythagorean Theorem to all triangles.

For any triangle with sides a, b, and c,ifθ is the angle opposite side c, then

= a

+ b

− 2ab cos θ

The proof is again due to Goldman (1987):

=B −A

= (B − A) · (B − A)

= [(B − C) +(C −A)]· [(B − C) +(C −A)]

= (B − C) ·(B − C) + (C − A) · (C − A) − 2(A − C)(B − C)

=B −C

+C −A

− 2A − CB − C cos C

= a

+ b

− 2ab cos C

B.3 Trigonometric Identities and Laws 939

Law of Tangents

The law of tangents states that in any triangle, the ratio of the difference between two

sides to their sum is the same as the ratio of the tangent of half the difference of the

opposite angles to the tangent of half their sum. Again, referring to Figure B.8, we

have

a +b

a −b

tan

α+β

tan

α−β

The proof, due to the “Math Forum” Web site (http://forum.swarthmore.edu/

dr.math), is as follows. Consider the addition and subtraction formulas for the sine

function:

sin(t + u) = sin(t) cos(u) + cos(t ) sin(u)

sin(t − u) = sin(t) cos(u) − cos(t ) sin(u)

Adding and subtracting, respectively, each of these with themselves gives

sin(t + u) + sin(t − u) = 2 sin(t) cos(u)

sin(t − u) + sin(t − u) = 2cos(t) sin(u)

If we let t = (α +β)/2 and u = (α −β)/2, then t + u = α and t − u = β, giving us

sin(α) + sin(β) = 2 sin((α + β)/2) cos((α −β)/2)

sin(α) + sin(β) = 2cos((α + β)/2) sin((α −β)/2)

We can then take the ratio of these two equations, giving us

tan((α +β)/2)

tan((α −β)/2)

sin((α +β)/2) cos((α − β)/2)

cos((α + β)/2) sin((α − β)/2)

2 sin((α + β)/2) cos((α − β)/2)

2cos((α +β)/2) sin((α −β)/2)

sin(α) + sin(β)

sin(α) − sin(β)

which, by the law of sines, is equal to

a +b

a −b

940 Appendix B Trigonometry

B.3.3 Formulas

This section presents a number of fundamental formulas that are occasionally useful

in solving geometric problems.

Mollweide’s Formula

If you are solving a problem consisting of computing vertices and/or edges of a

triangle, given (sufﬁcient) other information about the triangle, relationships such as

the laws of sines, cosines, and tangents can be used to ﬁnd the solution. Mollweide’s

and Newton’s formulas can be used to verify such solutions because they both involve

all three vertices and all three edges of the triangle.

b − c

sin

B−C

cos

Newton’s Formula

b + c

cos

B−C

sin

Area Formula

For right triangles, the area formula A = 1/2 base × height is easy to compute;

however, for a general triangle it is not so convenient. A more general formula may

be used instead:

A =

bc sin α

ac sin β

ab sin γ

Addition and Subtraction Formulas

You frequently run into problems that require the use of trigonometric functions of

the sum or difference of two angles, where you already have values for the trigono-

metric functions for each angle individually. These are given below:

sin(α +β) = sin α cos β + cos α sin β

sin(α −β) = sin α cos β − cos α sin β

cos(α + β) = cos α cos β − sin α sin β

cos(α − β) = cos α cos β + sin α sin β

B.3 Trigonometric Identities and Laws 941

tan(α +β) =

tan α + tan β

1 − tan α tan β

tan(α −β) =

tan α − tan β

1 + tan α tan β

cot(α +β) =

cot α cot β −1

cot α + cot β

cot(α −β) =

cot α cot β +1

cot α − cot β

You also run into problems that require the use of sums of trigonometric func-

tions of two angles:

sin α + sin β = 2 sin

α + β

cos

α − β

sin α − sin β = 2cos

α + β

sin

α − β

cos α +cos β = 2cos

α + β

cos

α − β

cos α −cos β =−2 sin

α + β

sin

α − β

tan α + tan β =

sin (α + β)

cos α cos β

tan α − tan β =

sin (α − β)

cos α cos β

Product Formulas

sin α sin β = cos

α − β

− cos

α + β

sin α cos β = sin

α + β

+ sin

α − β

cos α cos β = cos

α − β

+ cos

α + β

cos α cos β = cos

α + β

− cos

α − β

942 Appendix B Trigonometry

Double-Angle Formulas

sin 2α = 2 sin α cos α

2 tan α

1 + tan

cos 2α =cos

α − sin

= 2cos

α − 1

= 1 − 2 sin

1 − tan

1 + tan

tan 2α =

2 tan α

1 − tan

cot 2α =

cot

α − 1

2cotα

Triple-Angle Formulas

sin 3α =3 sin α −4 sin

cos 3α = 4cos

α − 3cosα

tan 3α =

3 tan α −tan

1 − 3 tan

Quadruple-Angle Formulas

sin 4α = 4 sin α cos α −8 sin

α cos α

cos 4α =8cos

α − 8cos

α + 1

tan 4α =

4 tan α − 4 tan

1 − 6 tan

α + tan

B.3 Trigonometric Identities and Laws 943

General Multiple-Angle Formulas

There are two different approaches to deﬁning these. The ﬁrst is based on a series

involving powers of the functions

sin nα = n sin α cos

n−1

α −





sin

α cos

n−3

α +





sin

α cos

n−5

α − ...

cos nα =cos

α −





sin

α cos

n−2

α +





sin

α cos

n−4

α − ...

and the second is deﬁned in terms of combinations of lesser multiples:

sin nα = 2 sin (n − 1)α cos α − sin (n − 2)α

cos nα =2cos(n − 1)α cos α − cos (n − 2)α

tan nα =

tan (n − 1)α + tan α

1 − tan (n − 1)α tan α

Selected Exponential Formulas

sin

α =

1 − cos 2α

sin

α =

3 sin α −sin 3α

sin

α =

3 − 4 cos 2α +cos 4α

cos

α =

1 + cos 2α

cos

α =

3cosα +cos 3α

cos

α =

3 + 4 cos 2α +cos 4α

tan

α =

1 − cos 2α

1 + cos 2α