Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

924 Appendix B Trigonometry
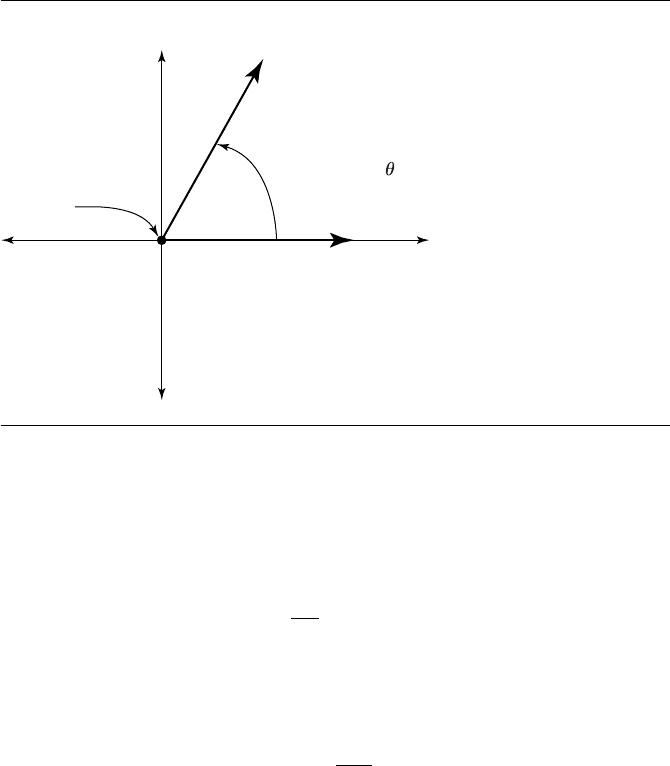
Vertex Initial side
Positive angle
Terminal side
x
y
Figure B.1 Standard terminology for angles.
of the ray describes a complete circle. The angle corresponding to this circle is defined
as being either 360 degrees or 2π radians:
1
◦
=
π
180
radians
≈ 0.017453 radians
and
1 radian =
180
◦
π
≈ 57.2958
◦
≈ 57
◦
17
44.8
Generally, if no units are given, an angle measure is considered to be in radians.
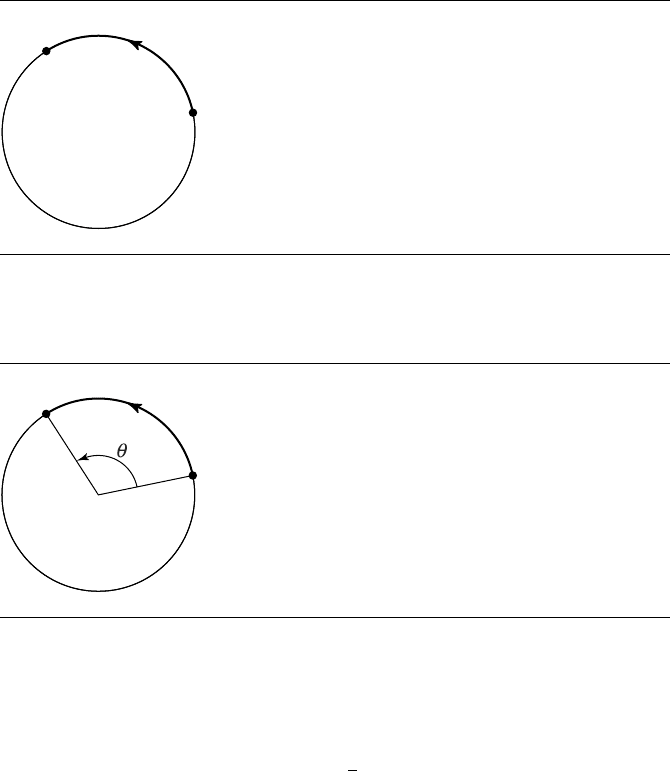
The definition of radians is not arbitrary—there is a reason why a full circle is
equivalent to 2π radians. First, we must define arc length: if we trace the path of a
point moving from A to B on a circle, then the distance traveled by that point is
some arc of the circle, and its length is the arc length, conventionally notated as s (see
Figure B.2).
B.1 Introduction 925
B
A
s
Figure B.2 Definition of arc length.
B
A
s
r
Figure B.3 Definition of radians.
Define
θ =
s
r
to be the radian measure of angle θ (Figure B.3), and consider the unit circle (where
r =1). Recall that the definition of π is the ratio of the circumference of a circle to its
diameter (i.e., 2r); the result is that there must be 2π radians in a full circle.
B.1.3 Conversion Examples
Problem: Convert 129
◦
to radians.
Solution: By definition

926 Appendix B Trigonometry
1
◦
=
π
180
radians
We can simply do a little arithmetic:
129
◦
=
π
180
· 129 radians
=
129
180
π radians
≈ 2.2514728 radians
Problem: Convert 5 radians to degrees.
Solution: By definition
1 radian =
180
π
◦
We can again simply do some arithmetic:
5 radians =
5 ·
180
π
◦
=
900
π
◦
≈ 286.47914
◦
B.2 Trigonometric Functions
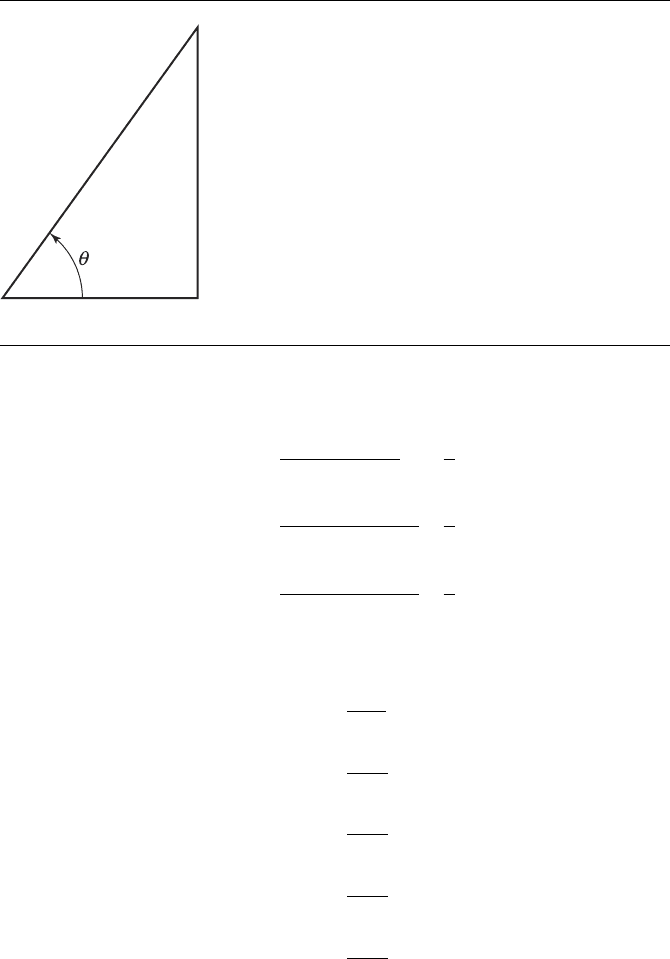
The standard trigonometric functions sine, cosine, tangent, cosecant, secant, and
cotangent may for (positive, acute) angle θ be defined in terms of ratios of the lengths
of the sides of a right triangle (see Figure B.4):
sin θ =
side opposite θ
hypotenuse
=
y
r
cos θ =
side adjacent to θ
hypotenuse
=
x
r
tan θ =
side opposite θ
side adjacent to θ
=
y
x
B.2 Trigonometric Functions 927
x
y
r
Figure B.4 The ratios of sides of a right triangle can be used to define trig functions.
csc θ =
hypotenuse
side opposite θ
=
r
y
sec θ =
hypotenuse
side adjacent to θ
=
r
x
cot θ =
side adjacent to θ
side opposite θ
=
x
y
Inspection of the above definitions reveals the following:
csc θ =
1
sin θ
sec θ =
1
cos θ
cot θ =
1
tan θ
tan θ =
sin θ
cos θ
cot θ =
cos θ
sin θ
A convenient mnemonic for remembering these is the phrase soh cah toa, for “sine
equals opposite over hypotenuse, cosine equals adjacent over hypotenuse, tangent
928 Appendix B Trigonometry
x
y
(x, y)
Figure B.5 Generalized definition for trigonometric functions.
equals opposite over adjacent”; csc, sec, and cot can be recalled simply as “1 over” the
appropriate one of the three basic functions.
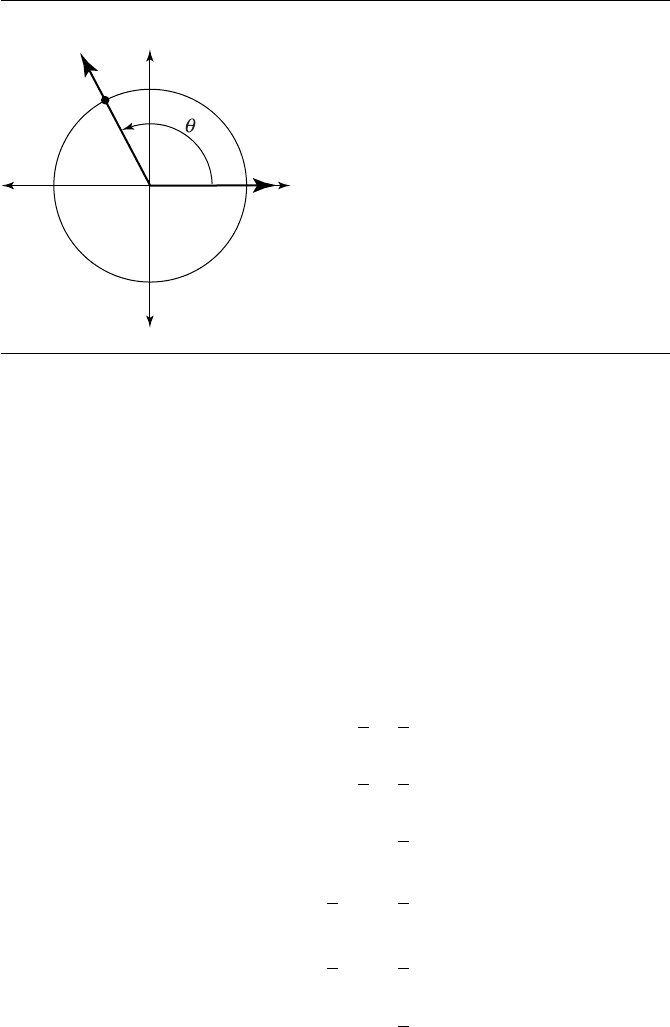
Note, however, that the above definitions only are valid for acute angles in stan-
dard position. A more complete and formal set of definitions can be created by con-
sidering the following: for an arbitrary pair of rays sharing a common vertex, define
a coordinate system transform such that the angle is in standard position; then con-
struct a unit circle, centered at the origin, and mark the point at which the terminal
side intersects the circle (Figure B.5).
With this, we have the following definitions:
sin θ = y =
y
1
=
y
r
cos θ = x =
x
1
=
x
r
tan θ =
y
x
csc θ =
1
y
=
r
y
sec θ =
1
x
=
r
x
cot θ =
x
y
B.2 Trigonometric Functions 929
Ta b l e B . 1
Trigonometric function values for some commonly used angles.
sin θ cos θ tan θ csc θ sec θ cot θ
0 = 0
◦
010—1—
π/12 = 15
◦
1
4
(
√
6 −
√
2)
1
4
(
√
6 +
√
2) 2 −
√
3
4
√
6−
√
2
4
√
6+
√
2
2 +
√
3
π/6 = 30
◦
1/2
√
3/21/
√
322/
√
3
√
3
π/4 = 45
◦
1/
√
21/
√
21
√
2
√
21
π/3 = 60
◦
√
3/21/2
√
32/
√
32 1
√
3
5π/12 = 75
◦
1
4
(
√
6 +
√
2)
1
4
(
√
6 −
√
2) 2 +
√
3
4
√
6+
√
2
4
√
6−
√
2
2 −
√
3
π/2 = 90
◦
10—1—0
7π/12 = 105
◦
1
4
(
√
6 +
√
2) −
1
4
(
√
6 −
√
2) −2 −
√
3
4
√
6+
√
2
−
4
√
6−
√
2
−2 +
√
3
2π/3 = 120
◦
√
3/2 −1/2 −
√
32/
√
3 −2 −1/
√
3
3π/4 = 135
◦
1/
√
2 −1/
√
2 −1
√
2 −
√
2 −1
5π/6 = 150
◦
1/2 −
√
3/2 −1/
√
32−2/
√
3 −
√
3
11π/12 = 165
◦
1
4
(
√
6 −
√
2) −
1
4
(
√
6 +
√
2) −2 −
√
3
4
√
6−
√
2
−
4
√
6+
√
2
−2 −
√
3
π = 180
◦
0 −10—−1—
3π/2 = 270
◦
−10—−1— 0
2π = 360
◦
010—1—
Note that the radius, which equals 1, corresponds to a hypotenuse of length 1 for
acute angles, and thus the final column can be observed to be equivalent to the ear-
lier definition. Note also that for angles that cause x or y to be zero, trigonometric
functions that divide by x or y, respectively, become undefined (see Table B.1).
An interesting and useful observation can be deduced from the equations above:
if we have an angle in standard position, then its terminal side intersects the unit circle
at the point (x, y) = (cos θ , sin θ). Further, all of the fundamental trigonometric
functions have a geometrical interpretation, as shown in Figure B.6.
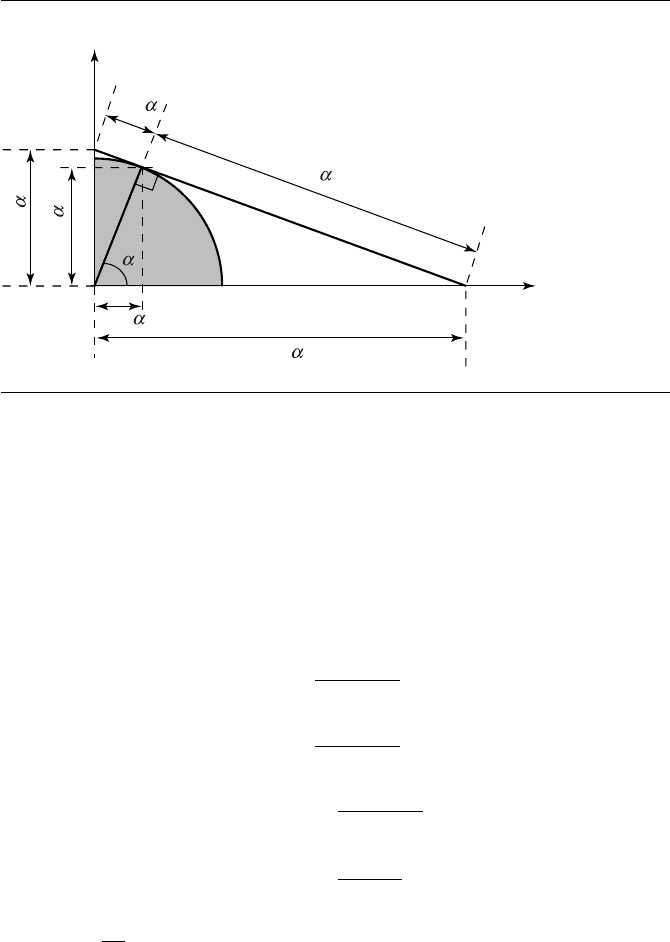
930 Appendix B Trigonometry
(1, 0)
y
x
tan
sec
cot
cos
csc
sin
Figure B.6 Geometrical interpretation of trigonometric functions.
B.2.1 Definitions in Terms of Exponentials
Interestingly, the basic trigonometric functions can be defined exactly in terms of e
sin α =
e
iα
− e
−iα
2i
cos α =
e
iα
+ e
−iα
2
tan α =−i
e
iα
− e
−iα
e
iα
+ e
−iα
=−i
e
2iα
− 1
e
2iα
+ 1
where i =
√
−1.
The value of e itself can be defined in terms of trigonometric functions:
e
iα
= cos α +i sin α

B.2 Trigonometric Functions 931
Ta b l e B . 2
Domains and ranges of trigonometric functions.
Domain Range
sin −∞ <x<∞−1 ≤ y ≤ 1
cos −∞<x<∞−1 ≤ y ≤ 1
tan −∞ <x<∞, x =
π
2
+ nπ −∞ <y<∞
sec −∞ <x<∞, x =
π
2
+ nπ |y|≥1
csc −∞<x<∞, x = nπ |y|≥1
cot −∞ <x<∞, x = nπ −∞ <y<∞
B.2.2 Domains and Ranges
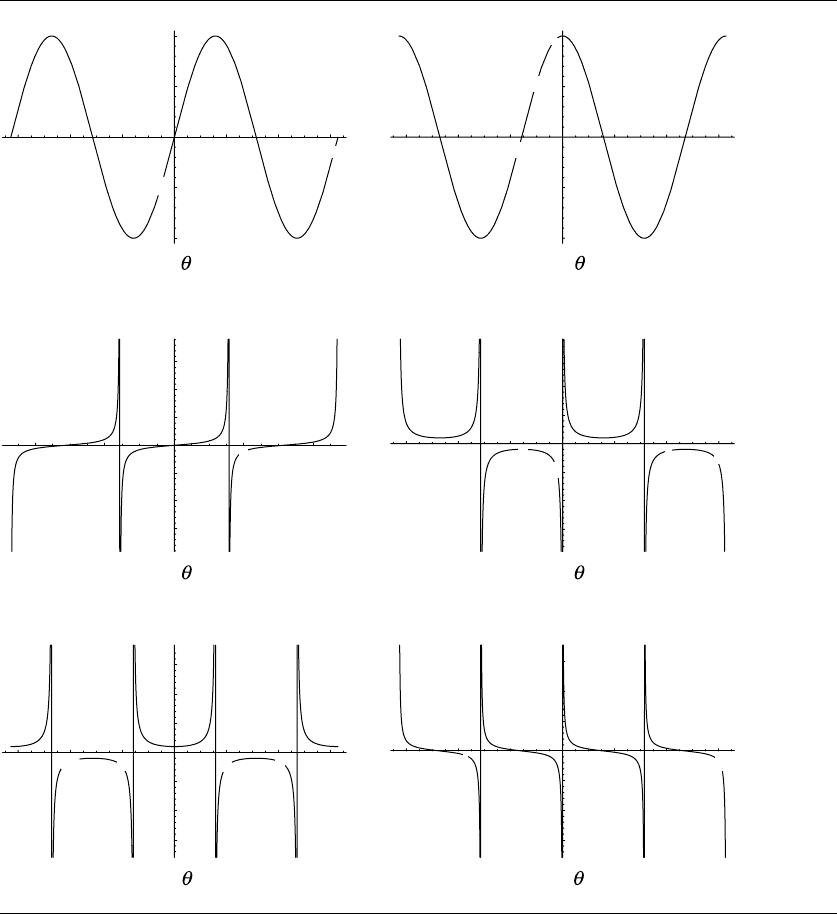
Table B.2 shows the ranges and domains of the fundamental trigonometric functions.
As can be observed in Figure B.7, generally the domains are infinite, with only some
discrete special values excluded in all but the sin and cos functions.
B.2.3 Graphs of Trigonometric Functions
Figure B.7 shows a portion of the graphs of each of the fundamental trigonometric
functions.
B.2.4 Derivatives of Trigonometric Functions
The derivative of a function f , notated as f
,isdefinedas
f
(x) = lim
n→0
f(x + h) − f(x)
h
We can find the derivative of the trigonometric functions by substituting each
function into this definition and using the trigonometric addition formulas along
with some simple manipulations to simplify them. For example,
d
dx
(sin x) = lim
n→0
sin(x + h) − sin x
h
= lim
n→0
sin x cos h + cos x sin h − sin x
h
= lim
n→0
sin x
cos h − 1
h
+ cos x
sin h
h
932 Appendix B Trigonometry
– 0.5
– 6 – 4 –2 2 4 6
–30
–20
–10
10
20
30
– 6 – 4 –2 2 4 6246
–1
– 0.5
0.5
1
– 4 –2
–30
–20
–10
10
20
30
– 6 –2 6
–15
–10
–5
5
10
15
–15
–10
5
10
15
–1
0.5
– 4–6
4
–2246– 4–62
–5
– 4 2 4
–2
cos
sin
tan
csc
cot
sec
Figure B.7 Graphs of the fundamental trigonometric functions.
B.2 Trigonometric Functions 933
The sin x and cos x terms are constants with respect to h,so
lim
n→0
sin x =sin x
lim
n→0
cos x = cos x
and thus
d
dx
(sin x) = sin x · lim
n→0
cos h − 1
h
+ cos x · lim
n→0
sin h
h
It can be shown that
lim
n→0
cos h − 1
h
= 0
lim
n→0
sin h
h
= 1
and so
d
dx
[
sin x
]
= cos x
The derivative for cos x can be computed similarly, resulting in
d
dx
[
cos x
]
=−sin x
The remaining trigonometric functions can be defined as simple fractions in-
volving sin and cos (see Section B.2.1).We can simply invoke the quotient rule from
calculus and compute
d
dx
[
tan x
]
= sec
2
x
d
dx
[
cot x
]
=−csc
2
x
d
dx
[
sec x
]
= sec x tan x
d
dx
[
csc x
]
=−csc x cot x
