Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.


944 Appendix B Trigonometry
General Exponential Formulas
sin
2n
α =
2n
n
1
2
2n
+
1
2
2n−1
n
k=1
(−1)
k
2n
n − k
cos 2kα
sin
2n−1
α =
1
2
2n−2
n
k=1
(−1)
k
2n − 1
n − k
sin (2k − 1)α
cos
2n
α =
2n
n
1
2
2n
+
1
2
2n−1
n
k=1
2n
n − k
cos 2kα
cos
2n−1
α =
1
2
2n−2
n
k=1
2n − 1
n − k
sin (2k − 1)α
Half-Angle Formulas
sin
α
2
=±
1 − cos α
2
cos
α
2
=±
1 + cos α
2
tan
α
2
=
sin α
1 + cos α
=
1 − cos α
sin α
=±
1 − cos α
1 + cos α
cot
α
2
=
sin α
1 − cos α
=±
1 + cos α
1 − cos α

B.4 Inverse Trigonometric Functions 945
B.4 Inverse Trigonometric Functions
You may intuit that, since the trigonometric functions are functions, they of course
have inverses. Computation of values of inverse trigonometric functions are fre-
quently useful in computer graphics; for example, you may come upon a problem
in which the expression
a =tan b
appears. Of course, if we have a but need b, we need to instead take the inverse of the
tangent function:
b = tan
−1
a
The inverses of the fundamental trigonometric functions have names consisting
of the fundamental name with the prefix arc: arcsine, arccosine, and so on. There are
two common sets of mathematical notations for this:
arcsin, arccos, arctan, etc.
sin
−1
,cos
−1
, tan
−1
,etc.
B.4.1 Defining arcsin and arccos in Terms of arctan
Interestingly, arcsin and arccos may be defined with formulas involving only inverse
tangents:
arcsin x =arctan
x
√
1 − x
2
arccos x =
π
2
− arctan
x
√
1 − x
2
B.4.2 Domains and Ranges
The domains of the inverse trigonometric functions are generally more restricted
than their counterparts. The graphs of these functions show this; see Table B.3 for
the exact values.

946 Appendix B Trigonometry
Ta b l e B . 3 Domains and ranges of inverse trigonometric functions.
Domain Range
sin
−1
−1 ≤ x ≤ 1 −
π
2
≤ y ≤
π
2
cos
−1
−1 ≤ x ≤ 10≤ y ≤ π
tan
−1
−∞ <x<∞−
π
2
≤ y ≤
π
2
sec
−1
|x|≥10≤ y ≤ π, y =
π
2
csc
−1
|x|≥1 −
π
2
≤ y ≤
π
2
, y = 0
cot
−1
−∞ <x<∞ 0 <y<π
B.4.3 Graphs
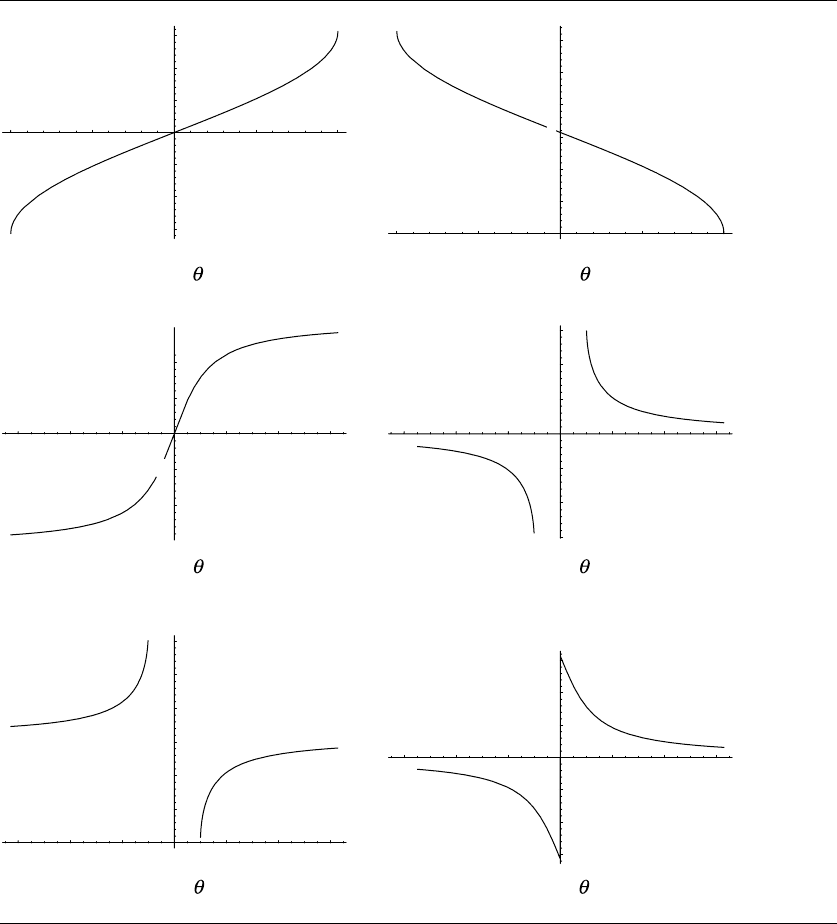
Figure B.10 shows a portion of the graphs of each of the fundamental inverse trigono-
metric functions.
B.4.4 Derivatives
d
dx
sin
−1
x
=
1
√
1 − x
2
d
dx
cos
−1
x
=−
1
√
1 − x
2
d
dx
tan
−1
x
=
1
1 + x
2
d
dx
cot
−1
x
=−
1
1 + x
2
d
dx
sec
−1
x
=
1
|x|
√
x
2
− 1
d
dx
csc
−1
x
=−
1
|x|
√
x
2
− 1
B.4 Inverse Trigonometric Functions 947
–2 2 4 6
–1.5
–1
– 0.5
0.5
1
1.5
–1 –0.5 0.5 1
0.5
1
2
2.5
3
–2 2 4 6
–1.5
–1
– 0.5
0.5
1
1.5
–1 – 0.5 0.5 1
–1.5
–1
– 0.5
0.5
1
1.5
– 6 – 4 –2 2 4 6
–1
0.5
1
– 6 – 4 –2 2 4 6
0.5
1
1.5
2
2.5
3
1.5
– 6 – 4
– 6 – 4
– 0.5
cos
–1
sin
–1
tan
–1
csc
–1
cot
–1
sec
–1
Figure B.10 Graphs of the fundamental inverse trigonometric functions.
948 Appendix B Trigonometry
B.4.5 Integration
sin
−1
udu= u sin
−1
u +
1 − u
2
+ C
cos
−1
udu= u cos
−1
u +
1 − u
2
+ C
tan
−1
udu= u tan
−1
u − ln
1 + u
2
+ C
cot
−1
udu= u cot
−1
u + ln
1 + u
2
+ C
sec
−1
udu= u sec
−1
u − ln
u +
u
2
− 1
+ C
csc
−1
udu= u csc
−1
u + ln
u +
u
2
− 1
+ C
B.5 Further Reading
The Web site of Wolfram Research, Inc. (http://functions.wolfram.com/Elementary
Functions) contains literally hundreds of pages of information regarding trigonomet-
ric functions. Textbooks on trigonometry abound: a recent search on www.amazon
.com for books whose subject contained the word “trigonometry” yielded 682 entries.

Appendix
CBasic Formulas
for Geometric
Primitives
C.1 Introduction
This appendix contains some useful formulas for various properties of common
geometric objects.
C.2 Triangles
C.2.1 Symbols
a, b, c: sides
α, β, γ : angles
h: altitude
m: median
s: bisector
2p = a +b + c: perimeter
A:area
R: circumradius (radius of circle passing through all three vertices)
C
R
: circumcenter (center of circle passing through all three vertices)
949
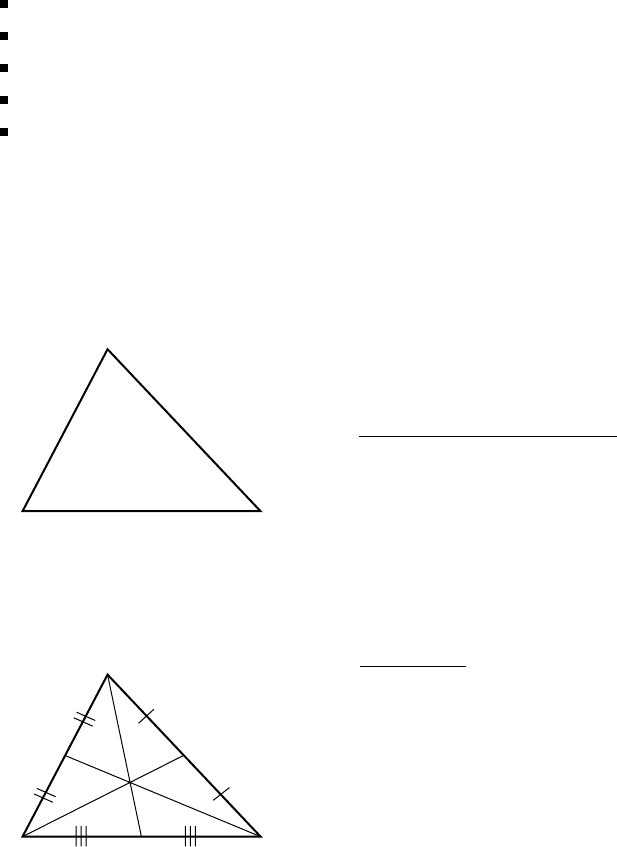
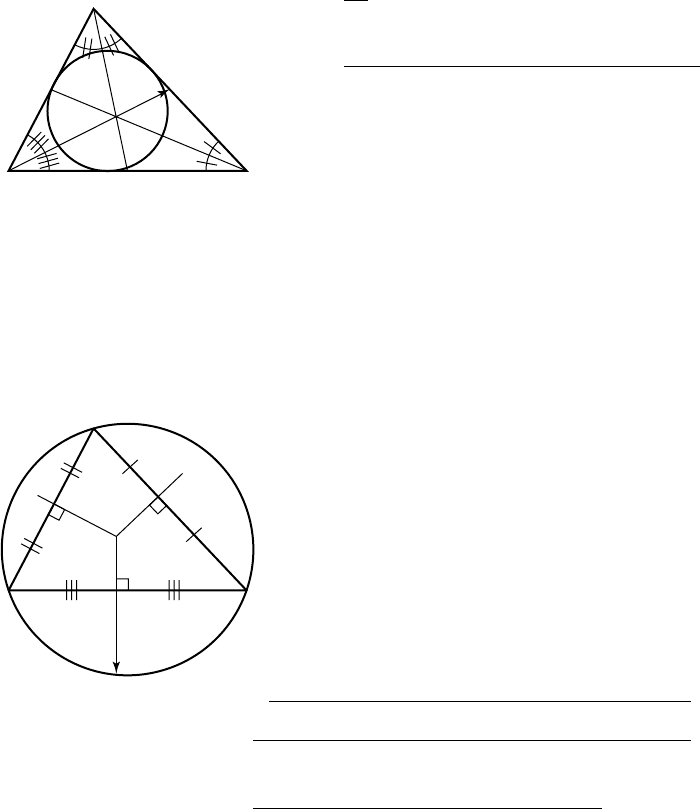
950 Appendix C Basic Formulas for Geometric Primitives
r: inradius (radius of circle tangent to all three sides)
C
r
: incenter (center of circle tangent to all three sides)
C
g
: center of gravity (intersection of the medians)
C
alt
: intersection of the altitudes
V
1
, V
2
, V
3
:vertices
C.2.2 Definitions
Perimeter and Area
V
3
V
1
V
2
a
b
c
2p = a +b + c
=V
1
− V
2
+V
2
− V
3
+V
3
− V
1
A =
V
1
× V
2
+ V
2
× V
3
+ V
3
× V
1
2
Intersection of Medians: Center of Gravity
V
3
V
1
V
2
C
g
1
2
C
g
=
V
1
+ V
2
+ V
3
3
C.2 Triangles 951
Intersection of Angle Bisectors: Inradius and Incenter
V
3
V
1
V
2
C
r
r
r =
2A
2p
C
r
=
V
2
− V
3
V
1
+V
3
− V
1
V
2
+V
1
− V
2
V
3
2p
Intersection of Perpendicular Bisectors: Circumradius
and Circumcenter
V
3
V
1
V
2
C
R
R
d
ca
=
V
3
− V
1
·
V
2
− V
1
d
ba
=
V
3
− V
2
·
V
1
− V
2
d
cb
=
V
1
− V
3
·
V
2
− V
3
n
1
= d
ba
d
cb
n
2
= d
cb
d
ca
n
3
= d
ca
d
ba
R =
d
ca
+ d
ba
d
ba
+ d
cb
d
cb
+ d
ca
/
n
1
+ n
2
+ n
3
2
C
R
=
n
2
+ n
3
V
1
+
n
3
+ n
1
V
2
+
n
1
+ n
2
V
3
2
n
1
+ n
2
+ n
3
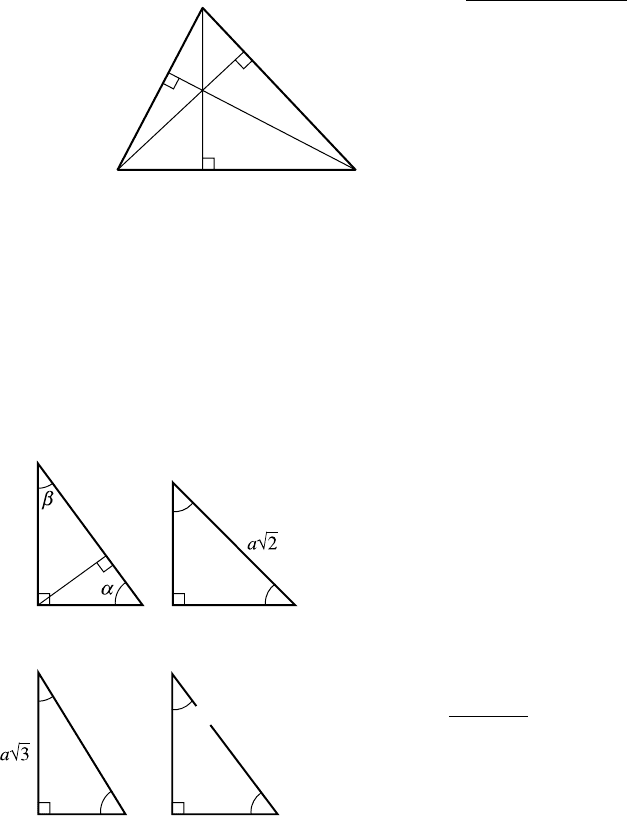
952 Appendix C Basic Formulas for Geometric Primitives
Intersection of Altitudes
V
3
V
1
V
2
C
alt
C
alt
=
n
1
V
1
+ n
2
V
2
+ n
3
V
3
n
1
+ n
2
+ n
3
C.2.3 Right Triangles
Here are some frequently useful right triangles:
b
c
e
d
h
aa
2a
60°
30°
45°
45°
~53.1301°
~36.8699°
a
4a 5a
a
3a
c
2
= a
2
+ b
2
A = ab/2
h = ab/c
d = a
2
/c
e = b
2
/c
R = c/2
r =
a +b − c
2
C.2 Triangles 953
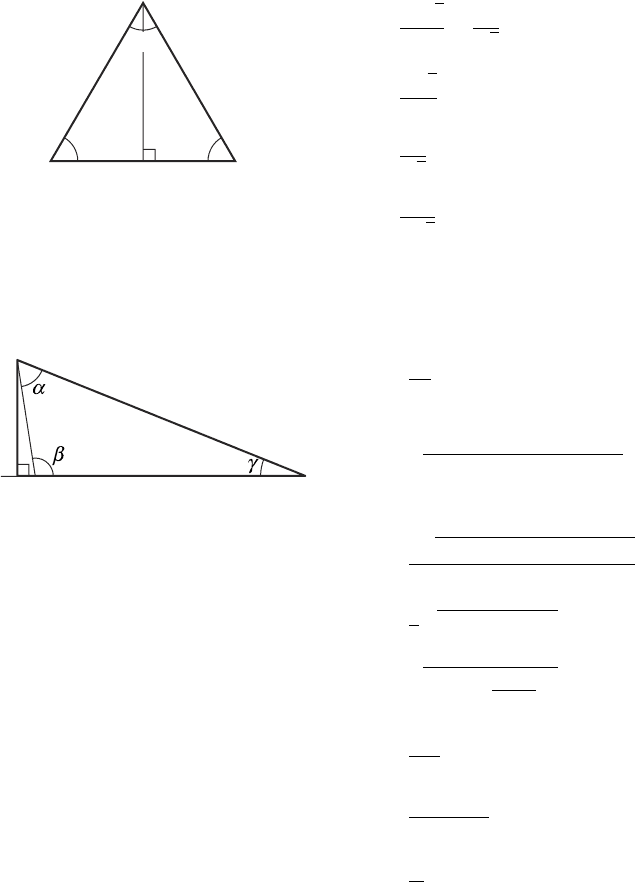
C.2.4 Equilateral Triangle
60° 60°
60°
h
aa
a
A =
a
2
√
3
4
=
h
2
√
3
h =
a
√
3
2
R =
a
√
3
r =
a
2
√
3
C.2.5 General Triangle
c
h
a
b
A =
ah
2
= bc sin α
=
p(p − a)(p −b)(p −c)
h
a
= c sin β
=
2
p(p − a)(p −b)(p −c)
a
m
a
=
1
2
2b
2
+ 2c
2
− a
2
s
a
=
bc[1 − (
a
b + c
)
2
]
R =
abc
4A
r =
2A
a +b + c
=
A
p
