Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

24 Chapter 2 Matrices and Linear Systems
[
ab
]
cd
ef
=
[
ac + be ad +bf
]
ce
df
a
b
=
ca + eb
da + fb
We’ll see later that computation of a function of a tuple is conveniently imple-
mented as a multiplication of the tuple by a matrix. Given the preceding discussion,
it should be clear that we could represent tuples as row or column matrices, and sim-
ply use the matrix or its transpose, respectively. In computer graphics literature, you
see both conventions being used, and this book also uses both conventions. When
reading any book or article, take care to notice which convention an author is using.
Fortunately, converting between conventions is trivial: simply reverse the order of the
matrices and vectors, and use instead the transpose of each. For example:
uM =
[
u
1
u
2
u
3
]
m
1,1
m
1,2
m
1,3
m
2,1
m
2,2
m
2,3
m
3,1
m
3,2
m
3,3
≡
m
1,1
m
2,1
m
3,1
m
1,2
m
2,2
m
3,2
m
1,3
m
2,3
m
3,3
u
1
u
2
u
3
= M
T
u
T
2.4 Linear Systems
Linear systems are an important part of linear algebra because many important prob-
lems in linear algebra can be dealt with as problems of operating on linear systems.
Linear systems can be thought of rather abstractly, with equations over real num-
bers, complex numbers, or indeed any arbitrary field. For the purposes of this book,
however, we’ll restrict ourselves to the real field R.
2.4.1 Linear Equations
Linear equations are those whose terms are each linear (the product of a real number
and the first power of a variable) or constant (just a real number). For example:
5x + 3 = 7
2x
1
+ 4 = 12 +17x
2
− 5x
3
6 −12x
1
+ 3x
2
= 42x
3
+ 9 −7x
1
2.4 Linear Systems 25
The mathematical notation convention is to collect all terms involving like vari-
ables (unknowns) and to refer to the equations in terms of the number of unknowns.
The preceding equations would thus be rewritten as
5x = 4
2x
1
− 12x
2
= 8
− 5x
1
+ 3x
2
− 42x
3
= 3
and referred to, respectively, as linear equations of one, two, and three unknowns.
The standard forms for linear equations in one, two, and n unknowns, respectively,
are
ax = c
a
1
x
1
+ a
2
x
2
= c
a
1
x
1
+ a
2
x
2
+···+a
n
x
n
= c
where the as are (given) real number coefficients and the xs are the unknowns.
Solving linear equations in one unknown is trivial. If we have an equation ax =c,
we can solve for x by dividing each side by a: x = c/a (provided a = 0).
Linear equations with two unknowns are a bit different: a solution consists of a
pair of numbers
x
1
, x
2
that satisfies the equation
a
1
x
1
+ a
2
x
2
= c
We can find a solution by assigning any arbitrary value for x
1
or x
2
(thus reducing it
to an equation of one unknown) and solve it as we did for the one-unknown case.
For example, if we have the equation
3x
1
+ 2x
2
= 6
we could substitute x
1
= 2 in the equation, giving us
3(2) + 2x
2
= 6
6 +2x
2
= 6
2x
2
= 0
x
2
= 0
So,
(
2, 0
)
is a solution. But, if we substitute x
1
= 6, we get
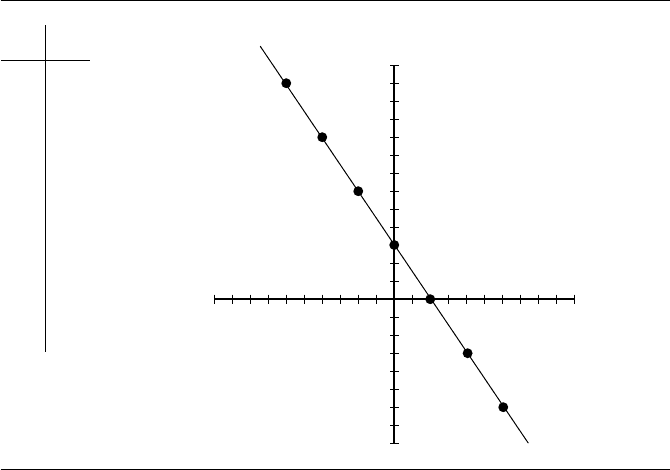
26 Chapter 2 Matrices and Linear Systems
(–6, 12)
(– 4, 9)
(–2, 6)
(0, 3)
(2, 0)
(4, –3)
(6, –6)
x
1
x
2
x
1
x
2
–6
–4
–2
0
2
4
6
12
9
6
3
0
–3
–6
Figure 2.2 The solutions of the linear equation 3x
1
+ 2x
2
= 6.
3(6) + 2x
2
= 6
18 + 2x
2
= 6
2x
2
=−12
x
2
=−6
yielding another solution u =
(
6, −6
)
. Indeed, there are an infinite number of solu-
tions. At this point, we can introduce some geometric intuition: if we consider the
variables x
1
and x
2
to correspond to the x-axis and y-axis of a 2D Cartesian coor-
dinate system, the individual solutions consist of points in the plane. Let’s list a few
solutions and plot them (Figure 2.2).
The set of all solutions to a linear equation of two unknowns consists of a line;
hence the name “linear equation.”
2.4.2 Linear Systems in Two Unknowns
Much more interesting and useful are linear systems—a set of two or more linear
equations. We’ll start off with systems of two equations with two unknowns, which
have the form
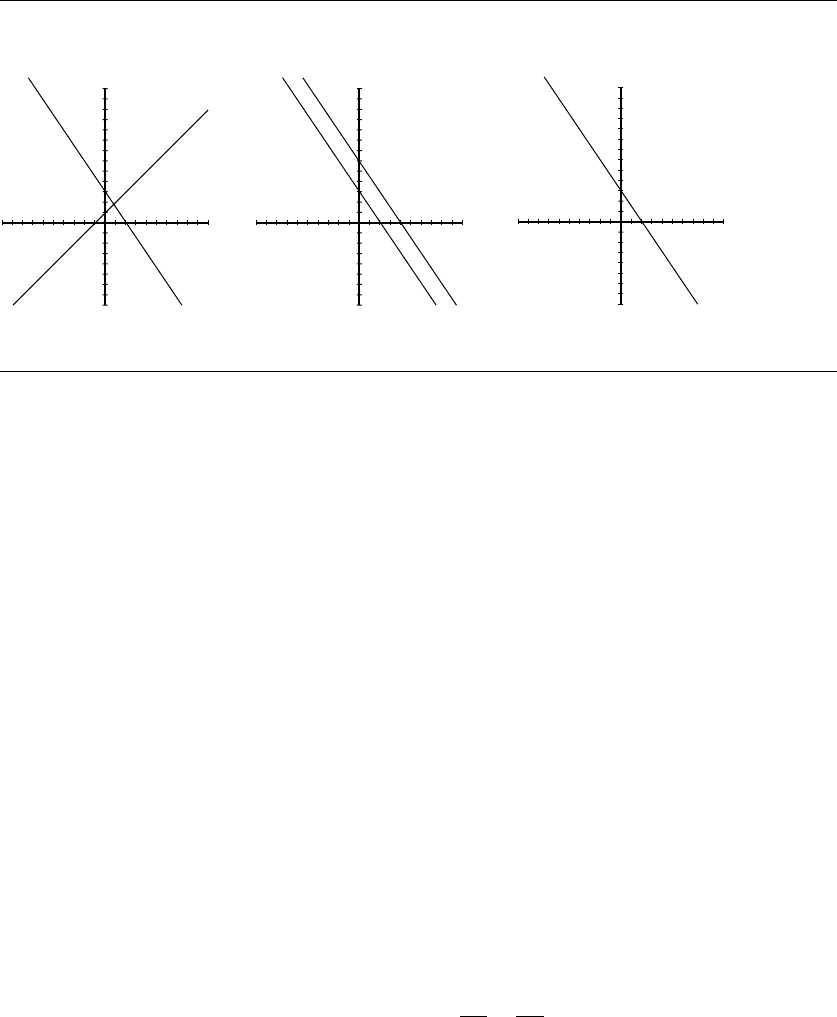
2.4 Linear Systems 27
3x + 2y = 6
x
y
x – y = 1
Unique solution
3x + 2y = 6
x
y
6x + 4y = 24
No solution
3x + 2y = 6
x
y
x + 2/3y = 2
Infinite number of solutions
Figure 2.3 Three possible two-equation linear system solutions.
a
1,1
x +a
1,2
y =c
1
a
2,1
x +a
2,2
y =c
2
Recall from our previous discussion that a two-unknown linear equation’s solu-
tion can be viewed as representing a line in 2D space, and thus a two-equation linear
system in two unknowns represents two lines. Even before going on, it’s easy to see
that there are three cases to consider:
i. The lines intersect at one point.
ii. The lines do not intersect—they’re parallel.
iii. The lines coincide.
Recalling that a solution to a single linear equation in two unknowns represents
a point on a line, the first case means that there is one u =
k
1
, k
2
point that is a
solution for both equations. In the second case, there are no points that are on both
lines; there is no solution to the system. In the third case, there are an infinite number
of solutions because any point on the line described by the first equation also satisfies
the second equation (see Figure 2.3). The second and third cases occur when the
coefficients in the two linear equations are proportional:
a
1,1
a
2,1
=
a
1,2
a
2,2

28 Chapter 2 Matrices and Linear Systems
What distinguishes the two cases is whether or not the constant terms are pro-
portional to the coefficients. The system has an infinite number of solutions (the two
lines are the same) if the coefficients and the constant terms are all proportional:
a
1,1
a
2,1
=
a
1,2
a
2,2
=
c
1
c
2
but no solutions (the lines are parallel) if the coefficients are proportional, but the
constants are not:
a
1,1
a
2,1
=
a
1,2
a
2,2
=
c
1
c
2
If there is a solution, it may be found by a process known as elimination:
Step 1. Multiply the two equations by two numbers so that the coefficients of one of
the variables are negatives of one another.
Step 2. Add the resulting equations. This eliminates one unknown, leaving a single
linear equation in one unknown.
Step 3. Solve this single linear equation for the one unknown.
Step 4. Substitute the solution back into one of the original equations, resulting in a
new single-unknown equation.
Step 5. Solve for the (other) unknown.
Example Given
(1) 3x +2y = 6
(2) x − y = 1
we can multiply (1) by 1 and (2) by −3 and then add them:
1 × (1): 3x +2y = 6
−3 × (2): −3x + 3y =−3
Sum: 5y = 3
which we solve trivially: y = 3/5. If we substitute this back into (1) we get
2.4 Linear Systems 29
3x + 2
3
5
= 6
3x +
6
5
= 6
3x =
24
5
x =
8
5
Thus (8/5, 3/5) is the solution, which corresponds to the point of intersection.
2.4.3 General Linear Systems
The general form of an m × n system of linear equations is
a
1,1
x
1
+ a
1,2
x
2
+···+a
1,n
x
n
= c
1
a
2,1
x
1
+ a
2,2
x
2
+···+a
2,n
x
n
= c
2
.
.
.
a
m,1
x
1
+ a
m,2
x
2
+···+a
m,n
x
n
= c
m
Asysteminwhichc
1
= c
2
=···=c
m
= 0 is known as a homogeneous system.
Frequently, linear systems are written in matrix form:
AX = C
a
1,1
a
1,2
··· a
1,n
a
2,1
a
2,2
··· a
2,n
.
.
.
a
m,1
a
m,2
··· a
m,n
x
1
x
2
.
.
.
x
n
=
c
1
c
2
.
.
.
c
m
The matrix A isreferredtoasthecoefficient matrix, and the matrix
a
1,1
a
1,2
··· a
1,n
c
1
a
2,1
a
2,2
··· a
2,n
c
2
.
.
.
a
m,1
a
m,2
··· a
m,n
c
m
is known as the augmented matrix.

30 Chapter 2 Matrices and Linear Systems
Methods for solving general linear systems abound, varying in generality, com-
plexity, efficiency, and stability. One of the most commonly used is called Gaussian
elimination—it’s the generalization of the elimination scheme described in the pre-
vious section. Full details of the Gaussian elimination algorithm can be found in
Section A.1 in Appendix A.
2.4.4 Row Reductions, Echelon Form, and Rank
We can look back at the example of the use of the technique of elimination for solving
a linear system and represent it in augmented matrix form:
326
1 −11
We then multiplied the second row by −3, yielding an equivalent pair of equations,
whose matrix representation is
326
−33−3
The next step was to add the two equations together and replace one of the equations
with their sum:
326
01
3
5
We then took a “shortcut” by substituting
3
5
into the first row and solving directly.
Note that the lower left-hand corner element of the matrix is 0, which of course
resulted from our choosing the multiplier for the second row in a way that the sum
of the first row and the “scaled” second row eliminated that element.
So, it’s clear we can apply these operations—multiplying a row by a scalar and
replacing a row by the sum of it and another row—without affecting the solution(s).
Another operation we can do on a system of linear equations (and hence the
matrices representing them) is to interchange rows, without affecting the solution(s)
to the system; clearly, from a mathematical standpoint, the order is not significant.
If we take these two ideas together, we essentially have described one of the
basic ideas of Gaussian elimination (see Section A.1): by successively eliminating
the leading elements of the rows, we end up with a system we can solve via back
substitution. What is important for the discussion here, though, is the form of the
system we end up with (just prior to the back-substitution phase); our system of
equations that starts out like this:

2.4 Linear Systems 31
a
1,1
x
1
+ a
1,2
x
2
+ a
1,3
x
3
+···+a
1,n
x
n
= c
1
a
2,1
x
1
+ a
2,2
x
2
+ a
2,3
x
3
+···+a
2,n
x
n
= c
2
.
.
.
a
m,1
x
1
+ a
m,2
x
2
+ a
m,3
x
3
+···+a
m,n
x
n
= c
m
ends up in upper triangular form, like this:
b
1,1
x
1
+ b
1,2
x
2
+ b
1,3
x
3
+···+b
1,n
x
n
= d
1
b
2,k
2
x
k
2
+ b
2,k
3
x
3
+···+b
2,n
x
n
= d
2
.
.
.
b
r,k
r
x
k
r
+···+b
r,n
x
n
= d
r
Notice that the subscripts of the last equation no longer involve m, but rather r<=m,
because this process may eliminate some equations: the process might sometimes
produce equations of the form
0x
1
+ 0x
2
+···+0x
n
= c
i
If c
i
= 0, then the equation can be eliminated entirely, without affecting the results;
if c
i
= 0, then the system is inconsistent (has no solution), and we can stop at that
point. The result is that successive applications of these operations on rows will tend
to make the system smaller.
Several other important statements can be made about the number r:
If r = n, then the system has a unique solution.
If r<n, then there are more unknowns than equations, which implies that there
are many solutions to the system.
In general, we call these operations elementary row operations—these are opera-
tions that can be applied to a linear system (and its matrix representation) that do
not change the solution set, and they may be codified as follows:
Exchanging two rows.
Multiplying a row by a (nonzero) constant.
Replacing a row by the sum of it and another row.
Combinations of operations that result in the elimination of at least one nonzero row
element are called row reductions.
32 Chapter 2 Matrices and Linear Systems
As the operations are applied to the various equations, we can represent this as
a series of transformations on the matrix representation of the system; a system of
equations, and the matrix representation of it, is in echelon form as a result of this
process (that is, once row reduction is complete, and the matrix cannot be further
reduced). The number of equations r of such a “completely reduced” matrix is known
as the rank of the matrix; thus, it may be said that the rank is an inherent property of
the matrix that’s only apparent once row reduction is complete.
The rank of a matrix is related to the concepts of basis, dimension, and linear
independence in the following way: the rank is the number of linearly independent
row (or column) vectors of the matrix, and if the rank is equal to the dimension, then
the rows of the matrix can be seen as a basis for a space defined by the matrix.
The preceding claim equating the rank with the number of linearly independent
rows of an echelon-form matrix follows from the fact that if two row vectors were not
linearly independent, that is,
a
1
v
i
+ a
2
v
j
= 0
for some a
1
, a
2
∈ R, then we could have properly applied a row reduction operation
to them, which would mean that the matrix was, contrary to our assumption, not in
echelon form.
2.5
Square Matrices
Within the general realm of linear algebra, square matrices are particularly signifi-
cant; this is in great part due to their role in representing, manipulating, and solving
linear systems. We’ll see in the next chapters that this significance extends to their role
in representing geometric information and their involvement in geometric transfor-
mations. We’ll start by going over some specific types of square matrices.
2.5.1 Diagonal Matrices
Diagonal matrices are those with 0 elements everywhere but along the diagonal:
M =
a
1,1
0 ··· 0
0 a
2,2
··· 0
.
.
.
.
.
.
.
.
.
.
.
.
00··· a
n,n
Diagonal matrices have some properties that can be usefully exploited:
2.5 Square Matrices 33
i. If A and B are diagonal, then C =AB is diagonal. Further, C can be computed
more efficiently than naively doing a full matrix multiplication: c
ii
= a
ii
b
ii
, and
all other entries are 0.
ii. Multiplication of diagonal matrices is commutative: if A and B are diagonal, then
C = AB =BA.
iii. If A is diagonal, and B is a general matrix, and C = AB, then the ith row of C is
a
ii
times the ith row of B;ifC =BA, then the ith column of C is a
ii
times the ith
column of B.
Scalar Matrices
Scalar matrices are a special class of diagonal matrices whose elements along the
diagonal are all the same:
M =
α 0 ··· 0
0 α ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
00··· α
Identity Matrices
Just as the zero matrix is the additive identity, there is a type of matrix that is the
multiplicative identity, and it is normally simply called I. So, for any matrix M,we
have IM = MI = M. Note that unlike the zero matrix, the identity matrix cannot be
of arbitrary dimension; it must be square, and thus is sometimes notated I
n
.For
an m × n matrix M,wehaveI
m
M = MI
n
= M. The identity matrix is one whose
elements are all 0s, except the top-left to bottom-right diagonal, which is all 1s; for
example:
I
2
=
10
01
I
3
=
100
010
001
In general, the form of an identity matrix is
I
n
=
10··· 0
01··· 0
.
.
.
.
.
.
.
.
.
.
.
.
00··· 1
A scalar matrix can be viewed as a scalar multiple of an identity matrix, that is, αI.
Note that multiplication by the identity matrix is equivalent to (scalar) multiplication
