Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

54 Chapter 2 Matrices and Linear Systems
which gives us v = [
11
] as an eigenvector for eigenvalue λ = 8. Similarly, if we
substitute λ = 2, we get
−4v
1
− 2v
2
= 0
−4v
1
− 2v
2
= 0
which gives us v = [
1 −2
] as an eigenvector for eigenvalue λ = 2. Note that any
scalar multiples of these eigenvectors are also eigenvectors for their associated eigen-
values.
This naturally extends to n × n arrays, whose characteristic equations are nth-
degree polynomials. Just as with any polynomial, there may be no, one, or up to n
real roots, and you should be aware that for n>4, no general closed-form solutions
exist. Fortunately, we most often deal with matrices of 4 × 4 and smaller in computer
graphics.
2.9 Euclidean Space
From the standpoint of computer graphics, the particular subclass of linear spaces
called Euclidean space is the most important. Our earlier discussions of linear spaces
didn’t include mention of “length” or “orthogonality,” instead focusing on vector
spaces in general.
2.9.1 Inner Product Spaces
We begin with a definition: Let V beavectorspaceoverR
n
.LetV
2
denote the set of
all pairs (u, v) where u, v ∈V .Aninner product is a function from V
2
to R, denoted
u, v, that satisfies the following conditions:
i. Distributivity: a
1
u
1
+ a
2
u
2
, v=a
1
u
1
, v+a
2
u
2
, v.
ii. Commutativity: u, v=v, u.
iii. Positive definiteness: u, u≥0, and u, u=0 ⇐⇒ u =
0.
Then, the space V is an inner product space. As suggested earlier, a vector space in
general may have elements of arbitrary type, but as we’re concerned with tuples of
real numbers, the remainder of this discussion makes this assumption.
Norm, Length, and Distance
There are infinitely many inner products of R
n
—that is, you can specify any arbitrary
function on such tuples that satisfy the conditions just described. The dot product

2.9 Euclidean Space 55
we first introduced in Section 2.3.4 is one particular choice of inner product; it has
properties that make it particularly useful. The third condition for the inner product
is involved with the definition of length; from it, we know that any nonzero vector has
a positive value as the inner product with itself. The square root of this inner product
is called the norm and is notated as
u=
u, u
As we’ll see later, the geometric “interpretation” of Euclidean space allows us to view
the norm as the length ofavector.
If the norm of a vector is 1, that is, u=1, then we say that the vector is normal-
ized. Any (nonzero) vector u ∈ V can be normalized by multiplying it by 1/u.The
distance between two vectors u, v ∈ V is defined as v −u. An inner product space
over R
n
whose inner product is the dot product is defined as a Euclidean space.
2.9.2 Orthogonality and Orthonormal Sets
Given a Euclidean space V , an inner product equal to 0 has particular significance:
if u, v=0, then they are called orthogonal.
Orthogonality has a particularly important role, relative to the concept of basis
vectors. Let V ={v
1
, v
2
, ..., v
n
} be a set of basis vectors for a vector space v.Ifwe
have v
i
, v
k
=0, ∀v
i
, v
k
∈ V, i = k, then the set V is itself called an orthogonal set.
If V is an orthogonal set of basis vectors, and v
i
=1, ∀v
i
∈V, then V is further
definedtobeorthonormal. A Euclidean space with a standard orthonormal frame is
known as Cartesian space.
Any Euclidean space has an infinite number of sets of basis vectors that define the
space. Any set of basis vectors may be orthogonal, orthonormal, or neither of these.
However, any set of basis vectors may be converted into an orthonormal set by means
of the Gram-Schmidt orthogonalization process.
Before we go into the orthogonalization process itself, we must understand a
property of orthonormal sets of basis vectors: an orthonormal set of vectors V
=
{v
1
, v
2
, ..., v
k
}, with k<n(the dimension of V ) because it is a subset of some set
of basis vectors, must be linearly independent; further, for any u ∈ V , the vector
w =u −u, v
1
v
1
−u, v
2
v
2
−···−u, v
k
v
k
(2.6)
is orthogonal to each v
i
∈ V
.
Let V be an inner product space, and V ={v
1
, v
2
, ..., v
n
} be a basis for it. We
can construct an orthonormal basis U ={u
1
, u
2
, ..., u
n
} using the Gram-Schmidt
orthogonalization process:
56 Chapter 2 Matrices and Linear Systems
Step 1. Set u
1
=
v
1
v
1
. Note that this makes u
1
unit length.
Step 2. Set u
2
=
v
2
−v
2
,u
1
u
1
v
2
−v
2
,u
1
u
1
. Note that u
2
is of unit length and (by Equation 2.6) is
orthogonal to u
1
. This makes the set {u
1
, u
2
} orthonormal.
Step 3. Set u
3
=
v
3
−v
3
,u
1
u
1
−v
3
,u
2
u
2
v
3
−v
3
,u
1
u
1
−v
3
,u
2
u
2
. Again, u
3
is unit length and (by Equation 2.6)
is orthogonal to u
1
and u
2
. Hence, the set {u
1
, u
2
, u
3
} is orthonormal.
Step 4. Repeat the previous step for the rest of the u
i
.
At the end of this process, we have an orthonormal basis for V .
2.10 Least Squares
The clever reader may have noted that all our linear systems so far have conveniently
had exactly as many equations as unknowns. So, as long as there exists a unique
solution, we can use one of several techniques to solve it. However, often situations
arise in which there are more equations than unknowns.
Consider a simple example: if we have two points and wish to determine the
equation of a line that passes through the points, we can set up a linear system to
solve; this system will have two equations and two unknowns, and so long as the
points are not coincident, a solution can be computed. For example, suppose we have
two points:
P
1
=
p
1,1
p
1,2
P
2
=
p
2,1
p
2,2
Of course, these define a line, which may be expressed as x
2
= mx
1
+ b.Wecan
solve for the coefficients m and b by representing the points as a linear system and
applying, say, Cramer’s rule. Our points must be on the line, and therefore satisfy the
line equation, and so we can write the linear system as
p
1,1
m + b = p
1,2
p
2,1
m + b = p
2,2
which in matrix form is
p
1,1
1
p
2,1
1
m
b
=
p
1,2
p
2,2
2.10 Least Squares 57
(x
1
, y
1
)
(x
2
, y
2
)
(x
3
, y
3
)
(x
1
, mx
1
+ b)
(x
2
, mx
2
+ b)
(x
3
, mx
3
+ b)
x
y
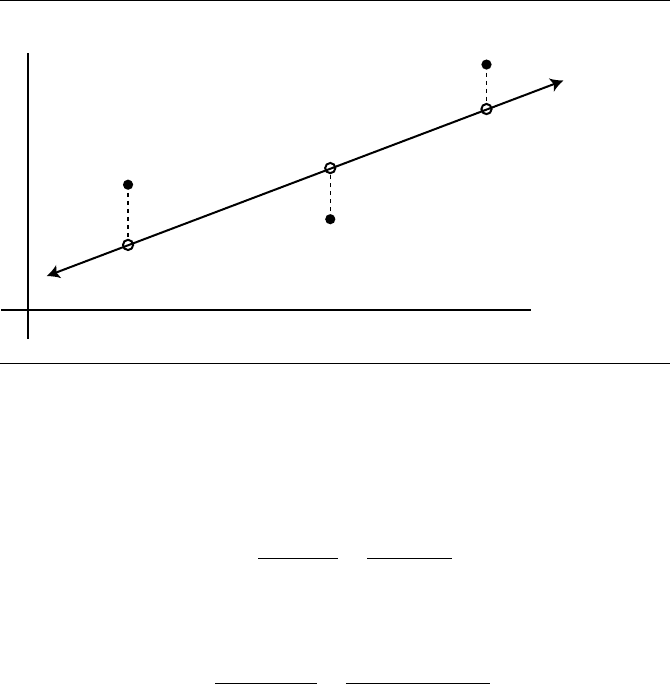
Figure 2.9
Least squares example.
Cramer’s rule has the solution as
m =
p
1,2
1
p
2,2
1
p
1,1
1
p
2,1
1
=
p
1,2
− p
2,2
p
1,1
− p
2,1
b =
p
1,1
p
1,2
p
2,1
p
2,2
p
1,1
1
p
2,1
1
=
p
1,1
p
2,2
− p
2,1
p
1,2
p
1,1
− p
2,1
However, consider if we have more than two points we wish to fit a line to; in
general, any three points in the plane will not be all on a line. In this case, we’d
like to have a line that minimizes the (vertical) distance between it and each of the
points. The line can be considered as a function f returning the y-value for a given
x-value (specifically, f(x)=mx +b). See Figure 2.9. We can represent this particular
example as a linear system:
p
1,1
m + b = p
1,2
p
2,1
m + b = p
2,2
p
3,1
m + b = p
3,2
58 Chapter 2 Matrices and Linear Systems
which in matrix form is
p
1,1
1
p
2,1
1
p
3,1
1
m
b
=
p
1,2
p
2,2
p
3,2
Note that we now have three equations, but only two unknowns; this is what’s called
an overdetermined system, and for these sorts of systems, the best we can generally
hope for is some sort of approximate solution, which satisfies some objective criteria.
The vertical distance D
1
, then, between a point
x
1
, y
1
and the line is
f(x
1
) − y
1
. For various reasons, we want to actually look at the sum of the squares
of the distances between the points and the line:
D
2
=
f(x
1
) − y
1
2
+
f(x
2
) − y
2
2
+···+
f(x
n
) − y
n
2
So, we want to choose the function (line) f so that D
2
is minimized. That is, we need
to choose m and b in an approximate way so that our objective criterion is met (the
minimization of D
2
). This is the reason this is called a least squares solution.
To understand how we go about solving this, you have to kind of stand on your
head for a while. Imagine a space R
n
of n dimensions, where n is the number of
points to fit (equations in the system). We can view the components of the coordi-
nates of a location y in this n-dimensional space as consisting of the y-values of the
points we’re trying to fit (that is, y =
y
1
, y
2
, ···, y
n
). Another location T(f)in this
n-dimensional space can be considered to have coordinates consisting of the y-values
of the points on the fitted line corresponding to each point we’re trying to fit; that is,
T(f)=
f(x
1
), f(x
2
), ···, f(x
n
)
. The total distance D
2
between the points and the
fitted line is thus the square of the distance (in the n-dimensional space R
n
)ofthe
vector T(f)− y.
In the case of our example of fitting a line to three points, the transformation T
corresponds to a matrix
M =
1 x
1
1 x
2
1 x
3
We need to find f (that is, m and b) such that we minimize D
2
(that is, T(f)−y).
If we represent this in matrix form, we get
2.10 Least Squares 59
M
[
f
]
−
[
y
]
= M
b
m
−
[
y
]
=
1 x
1
1 x
2
1 x
3
b
m
−
[
y
]
=
b + mx
1
− y
1
b + mx
2
− y
2
b + mx
3
− y
3
Recall that we need to minimize D
2
, which we wrote earlier as
D
2
=
f(x
1
) − y
1
2
+
f(x
2
) − y
2
2
+···+
f(x
n
) − y
n
2
in general, or specifically for our case
D
2
=
b + mx
1
− y
1
2
+
b + mx
2
− y
2
2
+
b + mx
3
− y
n
2
Since this is just a function, we know that the minimum occurs exactly when the
partial derivatives of D
2
with respect to b and m, respectively, are zero. This leads to
the system we need to solve:
b + mx
1
− y
1
+
b + mx
2
− y
2
+
b + mx
3
− y
3
= 0
x
1
b + mx
1
− y
1
+ x
2
b + mx
2
− y
2
+ x
3
b + mx
3
− y
3
= 0
If we rewrite this in matrix form we get
111
x
1
x
2
x
3
b + mx
1
− y
1
b + mx
2
− y
2
b + mx
3
− y
3
We can, for clarity, rewrite this as
111
x
1
x
2
x
3
1 x
1
1 x
2
1 x
3
b
m
−
y
1
y
2
y
3
=
0
0
60 Chapter 2 Matrices and Linear Systems
In this form, we can see that it incorporates our matrix M in various forms:
M
T
M
b
m
−
y
1
y
2
y
3
=
0
0
M
T
(
M
[
f
]
−
[
y
]
)
= 0
M
T
M
[
f
]
− M
T
[
y
]
= 0
Rearranging,
M
T
M
[
f
]
= M
T
[
y
]
[
f
]
=
M
T
M
−1
M
T
[
y
]
The astute reader may have noticed that the final manipulation to isolate [f ]
involved an operation that may not necessarily be justifiable—specifically, we’ve as-
sumed that we can invert the matrix M
T
M. Certainly it’s square, and it can be shown
that if the values x
1
, x
2
, and x
3
are distinct, the matrix can be inverted.
Recommended Reading
There are an enormous number of books on linear algebra; a recent search for the
string “linear algebra” on an Internet bookseller’s site yielded 465 entries. Particularly
appropriate are undergraduate texts in linear algebra, such as
Jeanne Agnew and Robert C. Knapp, Linear Algebra with Applications, Brooks/
Cole, Monterey, CA, 1978.
Howard Anton, Elementary Linear Algebra, John Wiley and Sons, New York, 2000.
Also quite useful and accessible is
Seymour Lipschutz, Schaum’s Outline of Theory and Problems of Linear Algebra,
McGraw-Hill, New York, 1968.
In the area of computer graphics, the following contain much of interest related
to linear algebra:
M. E. Mortenson, Mathematics for Computer Graphics Applications, Industrial
Press, New York, 1999 (Chapters 1–3).
Recommended Reading 61
James D. Foley, Andries van Dam, Steven K. Feiner, and John F. Hughes, Com-
puter Graphics: Principles and Practice, 2nd ed., Addison-Wesley, Reading, MA,
1996 (Appendix: Mathematics for Computer Graphics).
Gerald Farin and Dianne Hansford, The Geometry Toolbox for Graphics and Mod-
eling, A. K. Peters, Natick, MA, 1998.
Chapter
3Vector Algebra
3.1 Vector Basics
Before talking about vector spaces, let’s go back to basic principles. To keep things
concrete, we’ll talk physics. One fundamental class of physical properties and phe-
nomena can be described by a single value; for example, mass, volume, distance,
or temperature. However, a second class of properties or phenomena cannot be so
described; rather, they are by nature multiple-valued. One example of this class is
motion of an object, which has two components—speed and direction (as, say, kilo-
meters per hour and compass heading). The first class of properties can be called
scalar-valued, and the second class of properties can be called vector-valued.Vector-
valued entities may also be referred to as multidimensional, and the individual values
making up the entity are known as its components.
Later on, we’ll discuss some of the mathematics underlying these vector-valued
numbers, but for now let’s stick to a particular subclass defined by distance and
direction, which we’ll simply call vectors. To visualize this class of entities—these
vectors—we’ll draw them as arrows (directed line segments), as shown in Figure 3.1.
The direction is indicated by the orientation of these arrows, while distance is indi-
cated by their relative lengths.
3.1.1 Vector Equivalence
One of the most important characteristics of vectors is that of equivalence—what
does it mean to say that two vectors are equal or not? Recall that the components
of a vector are its direction and length; “position” is not part of the definition. In
Figure 3.1, vectors u and
t have different directions and lengths, and are thus different
63
