Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

44 Chapter 2 Matrices and Linear Systems

2.6.5 Linear Independence, Dimension, and Basis

The concept of linear combination arises frequently in linear algebra and is particu-

larly important in understanding linear independence and basis—two critical points

to an intuitive understanding of linear algebra.

Linear Independence

Suppose we have a vector space V . Given any set of vectors {v

, v

, ..., v

}, we can

classify them as either (linearly) independent or dependent. By deﬁnition, a set of

vectors is linearly dependent if there exist constants c

, c

, ..., c

, not all 0, such that

v

+ c

v

+···+c

v



and linearly independent if

v

+ c

v

+···+c

v



only when all the constants are 0.

An example of a linearly dependent set of vectors would be v

= (2, 5, 3), v

(1, 4, 0), and v

= (7, 22, 6) because the set of constants {2, 3, −1} leads to

2v

+ 3v

+−1v

= 2(2, 5, 3) + 3(1, 4, 0) +−1(7, 22, 6)

= (4, 10, 6) + (3, 12, 0) + (−7, −22, −6)



The preceding deﬁnition of linear dependence is fairly standard, but perhaps is

not the most intuitive, particularly for our purposes (which will become apparent

in a subsequent chapter). (Nonzero) vectors in a set {v

, v

, ..., v

} are linearly

independent if and only if none of the vectors is a linear combination of the others.

In the preceding example v

was a linear combination of v

and v

, with coefﬁcients 2

and 3, respectively. In fact, a somewhat stronger deﬁnition may be made: (Nonzero)

vectorsinaset{v

, v

, ..., v

} are linearly dependent if and only if one of them, say,

v

, is a linear combination of the preceding vectors:

v

+ c

v

+···+c

i−1

v

i−1

=v

Basis and Dimension

The concept of linear independence is important in deﬁning the dimension of a space.

By deﬁnition, if we have a set of vectors {v

, v

, ..., v

}, they are said to form a basis

2.7 Linear Mappings 45

for a linear space V if and only if they are both linearly independent and span the

space. The dimension of V is n, the number of such linearly independent vectors.

Several facts follow from this deﬁnition:

Any set of linearly independent vectors in V with fewer than n vectors fails to

span V .

Any set of vectors in V with greater than n vectors must be linearly dependent.

There is no unique basis for a space V of dimension n; there are an inﬁnite

number of such sets of basis vectors having n elements.

The concepts of subspace, span, linear combinations, and dimension are related

in the following way: let V be a vector space of dimension n spanned by, and deﬁned

as all linear combinations of, basis vectors V ={v

, v

, ..., v

}; then, if we select a set

of linearly independent vectors W ={w

, w

, ..., w

}∈V ,wherem<n, then the

set of all vectors that are linear combinations of W form a subspace W of V , having

dimension m.

2.7 Linear Mappings

In this section, we begin by reviewing the concept of mapping in general as a way of

leading into linear mappings, which are functions from one linear space to another.

We then show how matrices are used to represent linear mappings.

2.7.1 Mappings in General

The basic idea of a function is a rule that associates members of one set with members

in another set. The terms mapping, function, and transformation are all synonyms for

a particular type of such pairing of elements.

Deﬁnition

Let A and B be two sets with elements {a

, a

, ..., a

} and {b

, b

, ..., b

}, respec-

tively. A function T from A to B, written

T : A −→ B

is a set of pairs (a, b) such that a ∈ A and b ∈ B. Every pair in the set is unique, and

every element a ∈ A appears in exactly one pair in the set. The set A is called the

domain of the function, and the set B is called the range or co-domain. A function

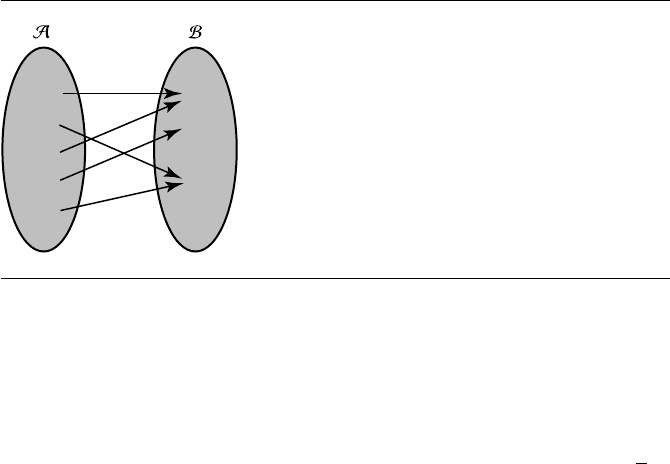
can be displayed schematically as in Figure 2.4.

For any element a ∈ A, the value in B that the function associates with a is

denoted T(a) or aT and called the image of a.Ifanelementb ∈ B is the image of

some a ∈ A, then that a is called the preimage of b. It is important to understand

that while every element a ∈A appears in the set of pairs, it is not necessarily true

46 Chapter 2 Matrices and Linear Systems

Figure 2.4 Schematic diagram of a function.

that every element b ∈ B appears. Indeed, a trivial function may map every element

in A to just a single element in B.

The domain and range of a function may be any sets of objects, whose elements

may be of the same type, or not. We can map real numbers to real numbers: for

example, T may be deﬁned as mapping a real number to its square root: x →

√

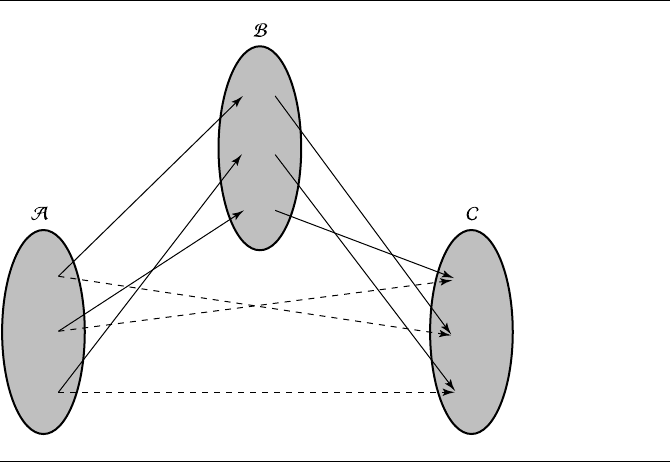
Composition of Mappings

Suppose we have two functions: T : A −→ B and U : B −→ C. By deﬁnition, for

every a ∈ A, there is some b ∈ B such that T(a)= b. Of course, the function U

maps that element b (the image of a)tosomeelementc ∈ C. The application of the

two functions T and U to a is called the composition of T and U and is denoted as

(U ◦ T )(a) = U(T(a))

(or a(T ◦ U) = aT U using the other convention), and we say

a → U(T(a))

Composition of mappings is associative. Suppose we have three functions: T :

A −→ B, U : B −→ C, and V : C −→ D. Then (V ◦ U) ◦ T = V ◦ (U ◦ T).A

schematic of a composition of two functions is shown in Figure 2.5.

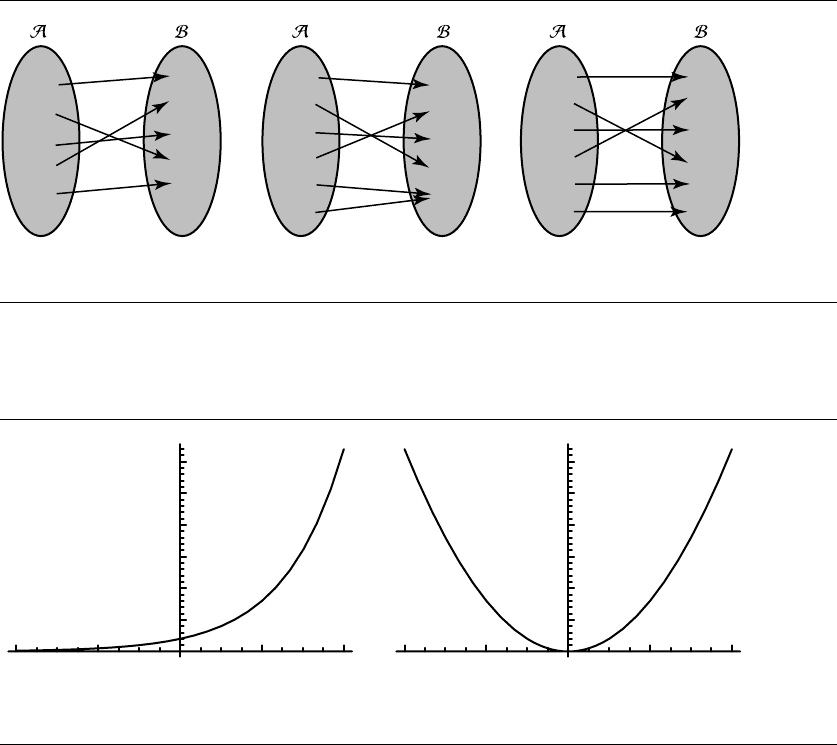
Special Types of Mappings

Three important classes of mappings are one-to-one, onto, and isomorphic (both

one-to-one and onto). These are shown schematically in Figure 2.6. A one-to-one

mapping T : A −→ B isoneinwhicheverya ∈A is associated with a unique b ∈B.

2.7 Linear Mappings 47

Figure 2.5 Composition of two functions.

An onto mapping T : A −→ B isoneinwhicheveryb ∈ B is the image of some

a ∈ A (or several). Examples of these functions are T(x)= 2

and T(x)= x

for

A being the set of real numbers and B being the set of positive real numbers in the

ﬁrst case, and B being the set of nonnegative real numbers in the second case (see

Figure 2.7).

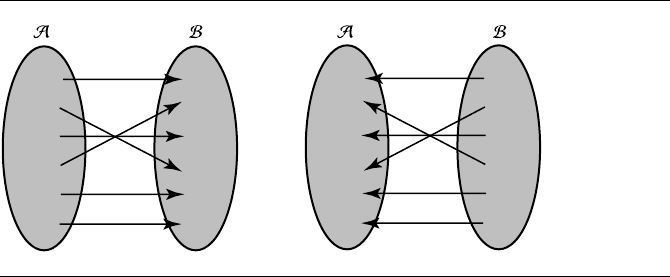
Inverse Mappings

Given a mapping T : A −→ B, it’s natural to consider the mapping that inverts

(reverses) T . Formally, a linear mapping T is invertible if there exists a mapping

−1

: B −→ A such that TT

−1

= I ,whereI is the identity mapping. As T

−1

is a

mapping, it must by deﬁnition have the entirety of B as its domain; further, every

element a ∈A must be in T

−1

’s range. These two facts show that a mapping must be

both one-to-one and onto for it to be invertible. See Figure 2.8.

2.7.2 Linear Mappings

Of course what we’re really interested in here are linear mappings; that is, mappings

relating linear spaces. Given two linear spaces A and B, a linear mapping T : A −→

B is a function that preserves vector addition and scalar multiplication:

48 Chapter 2 Matrices and Linear Systems

One-to-one Onto

One-to-one and onto

Figure 2.6 One-to-one, onto, and isomorphic maps.

–4 –224–4 –224

One-to-one: T(x) = 2

Onto: T(x) = x

2.5

7.5

12.5

2.5

7.5

12.5

Figure 2.7 One-to-one and onto functions.

i. ∀u, v ∈A, T(u +v) = T(u) + T(v).

ii. ∀α ∈R and ∀v ∈A, T(αv) = αT (v).

An important implication of this is that a linear mapping preserves linear combina-

tions: that is, T(αu + β v) = αT (u) + βT (v).

We discussed in the previous section that a mapping may be one-to-one or onto.

A linear function T : A −→ B is said to be an isomorphism if it is one-to-one and

maps A onto B.

2.7 Linear Mappings 49

–1

Figure 2.8 An invertible mapping.

An important aspect of linear mappings is that they are completely determined

by how they transform the basis vectors; this can be understood by recalling that any

vector v ∈V can be represented as a linear combination of the basis vectors, and that

linear mappings preserve linear combinations.

2.7.3 Matrix Representation of Linear Mappings

Linear mappings from R

to R

may be represented by matrices; that is, we can use

a matrix to specify how a vector in A ismappedtoavectorinB. We saw earlier that

a linear mapping is completely determined by its effects on the basis vectors, and it

is this fact that shows us how a matrix can be used to deﬁne (or implement) a linear

mapping.

Suppose we have linear spaces A and B with basis vectors u

, u

, ..., u

and

v

, v

, ..., v

and a linear mapping T : A −→ B. The transformed basis vectors

T(u

), T(u

), ..., T(u

) are elements in B, and therefore can be represented as some

linear combination of B’s basis vectors v

, v

, ..., v

T(u

) = a

1,1

v

+ a

1,2

v

+···+a

1,n

v

T(u

) = a

2,1

v

+ a

2,2

v

+···+a

2,n

v

T(u

) = a

m,1

v

+ a

m,2

v

+···+a

m,n

v

We can form the matrix T of coefﬁcients for the above; this is the matrix repre-

sentation of T relative to the bases of A and B:

50 Chapter 2 Matrices and Linear Systems

T =







1,1

1,2

··· a

1,n

2,1

2,2

··· a

2,n

m,1

m,2

··· a

m,n







This result leads to two important facts:

1. The (row) matrix representation of any vector in A can be transformed into the

space B by multiplying it by T:

T(x) =

[

··· x

]







1,1

1,2

··· a

1,n

2,1

2,2

··· a

2,n

m,1

m,2

··· a

m,n







2. The matrix representation of a composition of two linear mappings is the con-

catenation of the matrices representing each of the mappings: let a

, a

, ..., a

, b

, ..., b

, and c

, c

, ..., c

be the bases for linear spaces A, B, and C,re-

spectively, and let T : A −→ B and S : B −→ C be linear mappings with matrix

representations T and S, respectively. Then, R : A −→ C, the composition of T

and S, is represented by

S(T (v)) =v TS.

2.7.4 Cramer’s Rule

Cramer’s rule is a method for directly computing the solution to a system of linear

equations, provided one exists. To motivate this, let’s consider the case of a linear

system in two variables:

1,1

+ a

1,2

= c

2,1

+ a

2,2

= c

If we take the approach of using elimination, we multiply the ﬁrst equation by a

2,1

and the second equation by a

1,1

and subtract, and we get

2,1

1,1

+ a

2,1

1,2

= a

2,1

1,1

2,1

+ a

1,1

2,2

= a

1,1

2,1

1,2

− a

1,1

2,2

= a

2,1

− a

1,1

giving us

2.7 Linear Mappings 51

1,1

− a

2,1

1,1

2,2

− a

2,1

1,2

provided a

1,1

2,2

−a

2,1

1,2

=0. Substituting this value for x

back in the ﬁrst equation

yields

1,1

+ a

1,2

= c

1,1

+ x



1,1

− a

2,1

1,1

2,2

− a

2,1

1,2



= c

1,1

= c

−

1,2

1,1

− a

1,2

2,1

1,1

2,2

− a

1,2

2,1

1,1

2,2

− a

1,2

1,1

2,2

− a

1,2

2,1

2,2

− c

1,2

1,1

2,2

− a

1,2

2,1

provided a

1,1

2,2

−a

2,1

1,2

=0. The numerators and denominators of both x

and x

can be expressed as determinants:



1,2

2,2



1,1

1,2

2,1

2,2



, x



1,1

2,1



1,1

1,2

2,1

2,2



We can solve the example of Section 2.4.2 using Cramer’s rule. We have

3x + 2y =6

x −y =1

for which Cramer’s rule has



1 −1



1 −1



1 −1



52 Chapter 2 Matrices and Linear Systems

In its general form, Cramer’s rule is as follows: Let A denote the matrix of coefﬁ-

cients

A =

[

i,j

]

and let B

be the matrix formed by taking A and replacing column i by the column

of constants c

, c

, ···, c

. Then, if

= 0, there is a unique solution

u =





, ···,





It should be noted that Cramer’s rule can be unstable if the determinant of the

matrix is nearly zero, just as with other methods. There are two issues with respect

to Cramer’s rule for larger systems: ﬁrst, efﬁciency—for an n × n system, Cramer’s

rule is O(n!), while Gaussian elimination is O(n

); second, subtractive cancellation,

which in Gaussian elimination is handled with full pivoting.

2.8 Eigenvalues and Eigenvectors

Recall that we call n × 1 and 1 × n matrices vectors; without too much elaboration at

this point (we’ll discuss the geometric implications of linear algebra and vectors in a

subsequent chapter), you can think of a vector as specifying a direction and distance

in some “space” (such as Cartesian 2D space). Multiplying a vector by a matrix then

can be considered as transforming the direction and/or length of a vector. (Note that

we’re restricting our discussion to square matrices again).

We can represent this multiplication of vector v by the matrix M in the usual

fashion:

v



=vM

For some special vector v, we can ﬁnd a constant λ such that

v



= λv

and thus

vM = λv

Avectorv for which we can ﬁnd such a value λ is known as an eigenvector of M, and

the value λ is called an eigenvalue. Notice that since λ is a scalar, the value λv is simply

a scaled version of v, and thus whatever the multiplication by M does to an arbitrary

vector, it simply scales its eigenvectors.

2.8 Eigenvalues and Eigenvectors 53

The question now arises: how do we ﬁnd the eigenvalues for a particular matrix

M? Let’s do a little manipulation of the deﬁnition:

vM = λv (2.2)

v

(

λI −M

)



0 (2.3)

So long as v isn’t the



0 vector, it must be the case that

λI −M

= 0

which is known as the characteristic polynomial.

Here’s an example: let

M =





We’re looking for scalar λ such that vM = λv:

[

]





= λ

[

]

This corresponds to the linear system

+ 2v

= λv

(2.4)

+ 4v

= λv

(2.5)

which can be rewritten as the homogeneous system

(λ − 6)v

− 2v

= 0

−4v

+ (λ − 4)v

= 0

The determinant of the matrix of coefﬁcients for this system is zero if and only if the

linear system has a nonzero solution, so



λ − 6 −2

−4 λ − 4



= λ

− 10λ + 16 = (λ − 8)(λ − 2) = 0

and so the eigenvalues for M are λ

= 8 and λ

= 2.

If we substitute λ = 8 into Equation 2.4, we get

− 2v

= 0

−4v

+ 4v

= 0