Schinazi R.B. From Calculus to Analysis
Подождите немного. Документ загружается.

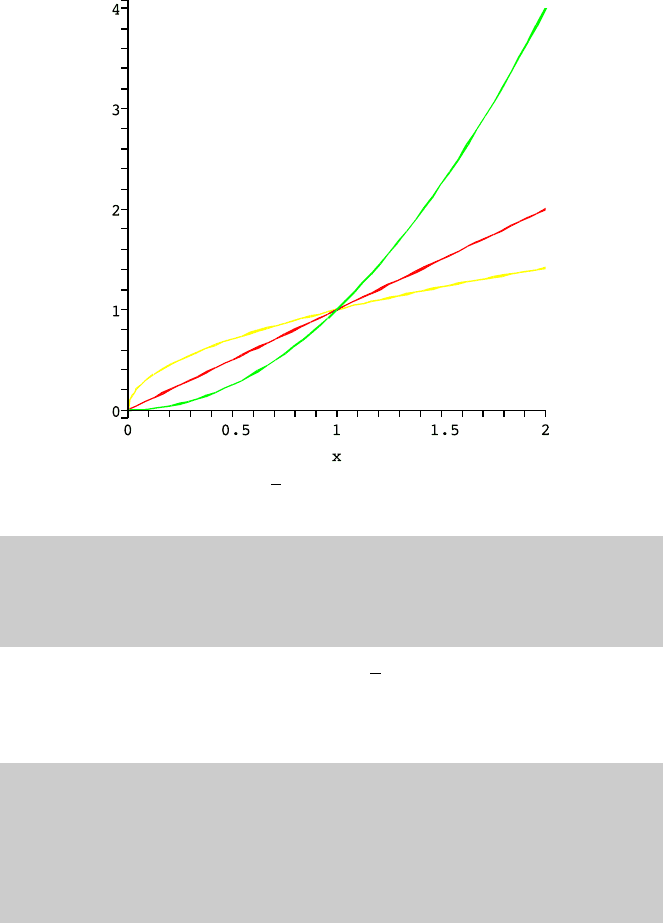
30 1 Number Systems
Fig. 1.1 These are the graphs of y =
√
x, y =x and y =x
2
Power functions
Let r =0 be a rational number. The function x →x
r
is defined on the positive
real numbers. It has an inverse function x →x
1/r
.
Figure 1.1 represents the graphs of y =
√
x, y = x, and y = x
2
. A number of
interesting facts are contained in this picture. In particular, if r<1, then x
r
>xfor
x<1 and x
r
<xfor x>1. If r>1, then x
r
<xfor x<1 and x
r
>xfor x>1.
Increasing power functions
Let r>0 be a rational number. The function x →x
r
is strictly increasing on
the positive real numbers. That is, for any real numbers 0 ≤a<b,
a
r
<b
r
.
This is in fact an easy consequence of the same property for natural powers I1.
We first prove the property in the particular case r =1/n. Assume that 0 <a<b,
and let n be a natural number. If a
1/n
≥b
1/n
, then we would have, by I1,
a
1/n
n
≥
b
1/n
n
,
and so a ≥b. This is a contradiction. Therefore, a
1/n
<b
1/n
.

1.4 Power Functions 31
We are now ready for the general case. Let r =m/n where m and n are natural
numbers. Assume that 0 <a<b. Then a
1/n
<b
1/n
and (a
1/n
)
m
<(b
1/n
)
m
.This
shows that a
r
<b
r
and concludes the proof that the function x → x
r
is increasing
on the positive reals when r>0.
We now give two more useful inequalities.
More Inequalities
I4 Let 0 <r<1 be a rational number, and 0 <a<1 be real number. Then
a
r
>a.
I5 Let 0 <r<1 be a rational number, and a>1 be real number. Then
a
r
<a.
We start by proving I4. Let r =p/q where p<qwith p and q natural numbers.
Since a<1, by I2,
a
q−p
<a<1.
Hence,
a
q−p
a
p
<a
p
,
and so a
q
<a
p
. Using that x →x
1/q
is strictly increasing, we get
a
q
1/q
<
a
p
1/q
.
That is,
a<a
r
.
This proves I4. The proof of I5 is similar and is left as an exercise.
We now have a mathematical definition for rational powers. But what does 3
√
2
mean? When we will introduce the exponential and logarithmic function in Chap. 3,
we will define, for a>0 and any real x,
a
x
=exp(x lna).
In particular,
3
√
2
=exp
√
2ln3
.
Exercises
1. Solve the inequality x
2
<x.
2. Solve the inequality x
3
>x
2
.
3. Show that for any real a,
√
a
2
=|a|. (Use that
√
b is the unique positive solution
of the equation x
2
=b.)
4. Show that if x and y are positive reals and x
r
=y
r
for some rational r =0, then
x =y.

32 1 Number Systems
5. (a) Prove P3 for natural powers.
(b) Prove P2 for rational numbers.
(c) Prove P3 for rational numbers.
6. Assume that a>1. Show that for natural numbers n and m, a
n
>a
m
if and
only if n>m.
7. Assume that a>1 is real and that the rationals s and t are such that s<t.
Prove that a
s
<a
t
. (Raise both quantities to the appropriate power and use
Exercise 6.)
8. Show that if the rational number r is negative, then the function x → x
r
is
decreasing on the positive reals. That is, show that if 0 ≤a<b, then a
r
>b
r
.
9. Prove I5.
10. Assume that the rational number r>1.
(a) Show that if a>1, then a
r
>a.
(b) Show that if a<1, then a
r
<a.
11. (a) Prove that 1 <
√
2 < 2.
(b) Find two rationals r
1
and r
2
such that r
1
<
√
2 <r
2
and r
2
−r
1
< 1/100.
12. Show that x →
1
√
1+x
2
is a decreasing function on the positive reals.

Chapter 2
Sequences and Series
2.1 Sequences
A sequence is a function from the positive integers (possibly including 0) to the
reals. A typical example is a
n
=1/n defined for all integers n ≥ 1. The notation a
n
is different from the standard notation for functions a(n) but means the same thing.
We now define convergence for sequences.
Convergent sequence
The sequence a
n
is said to converge to a real number a if for every >0,
there is a natural number N (that usually depends on ) such that if n ≥ N,
then
|a
n
−a|<.
a
n
converges to a is denoted by lim
n→∞
a
n
=a. The number a is called the
limit of the sequence a
n
.
Note that for sequences, one looks only at the limit as n goes to infinity. A se-
quence that does not converge is said to diverge. We will now study several exam-
ples.
Example 2.1 Consider a constant sequence a
n
= c for all n ≥ 1, where c is a con-
stant. Then, of course, a
n
converges to c:takeany>0, take N =1; then for every
n ≥N,wehave|a
n
−c|=0 <. Therefore, by definition, a
n
converges to c.
Example 2.2 Let a
n
= 1/n. Intuitively, it is clear that a
n
converges to 0. We now
prove this. Let >0. By the Archimedean property there is a natural N>1/.For
n ≥N,wehave1/n ≤ 1/N < (why?). Thus,
1/n =|a
n
−0|< for all n ≥N,
and we have proved that a
n
converges to 0.
R.B. Schinazi, From Calculus to Analysis,
DOI 10.1007/978-0-8176-8289-7_2, © Springer Science+Business Media, LLC 2012
33

34 2 Sequences and Series
Example 2.3 Assume that the sequence a
n
converges to .Letb
n
= a
n+1
. Let us
show that b
n
converges to the same .
Since a
n
converges to , for any >0, there is a natural N such that if n ≥ N,
then |a
n
−| <. Note that if n ≥N , then n +1 ≥N and |a
n+1
−| <as well.
That is, if n ≥N,wehave|b
n
−|<. This proves that b
n
converges to as well.
In order to prove that a sequence converges to 0, the following is sometimes
useful.
Convergence to 0
A sequence a
n
converges to 0 if and only if the sequence |a
n
| converges to 0.
Assume first that a
n
converges to 0. For any >0, there is N such that if n ≥N ,
then
|a
n
−0| <.
We have that
|a
n
−0|=|a
n
|=
|a
n
|−0
.
Hence,
|a
n
|−0
<
for all n ≥N . This proves that |a
n
| converges to 0.
Assume now that |a
n
| converges to 0. For any >0, there is N such that if
n ≥N, then
|a
n
|−0
<.
But ||a
n
|−0|=|a
n
−0|. Thus,
|a
n
−0|<
for all n ≥N . This proves that a
n
converges to 0 and completes the proof.
Example 2.4 Assume that a
n
converges to , and let c be a constant. Then ca
n
converges to c.
If c =0, then ca
n
is the constant sequence 0, and it converges to 0 =0 ·.Sothe
property holds when c =0. Assume now that c =0. Let >0; since a
n
converges
to , there is a natural N such that if n ≥N ,wehave
|a
n
−|<
|c|
.
Multiplying across this inequality by |c|, we get
|ca
n
−c|<.
This proves that ca
n
converges to c, and we are done.

2.1 Sequences 35
The next example shows that not all oscillating sequences diverge.
Example 2.5 Let a
n
=(−1)
n
/n. Show that a
n
converges to 0.
Observe that |a
n
|=1/n converges to 0. Thus, a
n
converges to 0.
We now turn to the notion of bounded sequence
Bounded sequences
A sequence a
n
is said to be bounded if there exists a real number K such that
|a
n
|<K for all n.
There is an important relation between bounded sequences and convergent se-
quences.
A convergent sequence is bounded
If a sequence converges, then it must be bounded.
We now prove that a convergent sequence is bounded. Assume that the sequence
a
n
converges to some limit a.Take =1; since a
n
converges to a, there is a natural
N such that if n ≥ N, then |a
n
− a| <= 1. Thus, by the triangle inequality we
have
|a
n
|=|a
n
−a +a|≤|a
n
−a|+|a|< 1 +|a| for all n ≥N.
The inequalities above show that the sequence is bounded for n ≥N .Wenowtake
care of n<N. We know that a finite set of real numbers always has a maximum
and a minimum. Thus, let
M =max
|a
1
|, |a
2
|,...,|a
N−1
|
,
and let K =max(M, 1 +|a|). Then, we claim that
|a
n
|<K for all n ≥1.
For if n<N, then |a
n
| <M≤ K, while if n ≥ N, then |a
n
| < |a|+1 ≤ K.This
completes the proof that a convergent sequence is bounded.
Example 2.6 Let c such that |c| > 1. Consider the sequence b
n
=c
n
for n ≥0. Let
us show that b
n
does not converge.
Let |c|=1 +a where a =|c|−1 > 0. By Bernoulli’s inequality we have
|b
n
|=|c|
n
=(1 +a)
n
≥1 +na.
Note that the sequence 1 + na is not bounded (why?), and therefore b
n
is not
bounded either. Therefore, it cannot converge.

36 2 Sequences and Series
A bounded sequence does not necessarily converge. In order to show that a se-
quence does not converge, the following notion of subsequence is quite useful.
Subsequences
Let 1 ≤ j
1
<j
2
< ···<j
n
< ···be a strictly increasing sequence of natural
numbers. Let a
n
be a sequence of real numbers. Then a
j
n
defines a new se-
quence of real numbers (it is in fact the composition of sequences a
n
and j
n
)
and is called a subsequence of a
n
. The name comes from the fact that all terms
a
j
n
are in the original sequence a
n
.
Useful examples of strictly increasing sequences of natural numbers are j
n
=n,
j
n
=2n, j
n
=2n +1, and j
n
=2
n
.
Subsequences and convergence
A sequence a
n
converges to a if and only if all the subsequences of a
n
con-
verge to a.
The proof is easy. First, the direct implication. Assume that a
n
converges to a,
and let a
j
n
be a subsequence of a
n
. For any >0, there is N such that if n ≥ N,
then |a
n
− a| <. It is easy to show (see the exercise ) that j
n
≥ n for all n ≥ 1.
Thus, if n ≥N , then j
n
≥n ≥N and |a
j
n
−a| <. Therefore, a
j
n
converges to a.
This proves that any subsequence of a
n
converges to a.
We now prove the converse. We assume that all subsequences of a
n
converge
to a.Buta
n
is a subsequence of itself (take j
n
=n), and thus a
n
converges to a and
we are done.
We use the preceding result in the next example.
Example 2.7 Let a
n
= (−1)
n
. Intuitively, it is clear that a
n
does not converge (it
oscillates between −1 and 1). We prove this. Note that the subsequence a
2n
is the
constant sequence 1 and so converges to 1. On the other hand, a
2n+1
is the constant
sequence −1 and so converges to −1. That is, we have found two subsequences that
converge to two distinct limits. This proves that (−1)
n
does not converge.
The following principle is sometimes quite useful.
Squeezing principle
Assume that the three sequences a
n
, b
n
, and c
n
are such that
a
n
≤b
n
≤c
n
and that the sequences a
n
and c
n
converge to the same limit . Then b
n
con-
verges to as well.
2.1 Sequences 37
The result above not only proves the convergence of b
n
, but it also gives the limit.
We now prove it. Recall that
|x|<a ⇐⇒ − a<x<a.
We start by writing that a
n
and c
n
converge to . For any >0, there are naturals
N
1
and N
2
such that if n ≥N
1
, then
|a
n
−|< ⇐⇒ −<a
n
<+,
and if n ≥N
2
, then
|c
n
−|< ⇐⇒ −<c
n
<+.
Define N =max(N
1
,N
2
), so that the two double inequalities above hold for n ≥N.
Thus, for n ≥N, using that b
n
is squeezed between a
n
and c
n
,wehave
−<a
n
≤b
n
≤c
n
<+.
But this implies that
−<b
n
<+ ⇐⇒ | b
n
−|< for all n ≥N.
That is, b
n
converges to , and the squeezing principle is proved.
Next we give an application of the squeezing principle.
Example 2.8 Assume that a
n
converges to 0 and that b
n
is bounded. Then a
n
b
n
converges to 0.
Since b
n
is bounded, there is B such that |b
n
|<B for all n. Then,
0 ≤|a
n
b
n
|≤B|a
n
|.
That is, the sequence |a
n
b
n
| is squeezed between the constant sequence 0 and the
sequence B|a
n
|. But they both converge to 0 (why?). By the squeezing principle,
|a
n
b
n
| converges to 0, and so does a
n
b
n
.
Example 2.9 Consider the sequence a
n
=n
r
where r is a rational number. Discuss
the convergence of a
n
in function of r.
If r =0, then a
n
is the constant sequence 1, and it converges to 1.
Assume that r>0. By contradiction, assume that the sequence a
n
= n
r
is
bounded. Then there is B>0 such that for all n, n
r
<B. Since 1/r > 0, the function
x → x
1/r
is increasing, and we have n<B
1/r
for all naturals n. This contradicts
the Archimedean property and shows that a
n
cannot be bounded. Hence, if r>0,
a
n
does not converge.
Let r>0. We now show that n
−r
converges to 0. Take any >0 and let N>
1/
1/r
; then for n ≥N,wehave
n
−r
−0
=1/n
r
≤1/N
r
<.
This proves that n
−r
converges to 0.

38 2 Sequences and Series
The following is a useful property of least upper bounds.
Least upper bound and sequences
Let A be a subset in the reals with a least upper bound m. There exists a
sequence a
n
in A that converges to m.
The important part of this property is that the sequence is in A. The same property
holds for the greatest lower bound, and the proof is left to the reader.
We now prove the property. Since m is the least upper bound of A, m −1 is not
an upper bound of A. Thus, there is at least one a in A such that a>m−1. We pick
one such a, and we denote it by a
1
. Similarly, m − 1/2 cannot be an upper bound
of A, so there is at least one a in A such that
a>m−1/2.
We pick one such a, and we call it a
2
. More generally, for every natural n, m −1/n
is not an upper bound of A, and we may pick a
n
in A such that
a
n
>m−1/n.
Hence, there exists a sequence a
n
in A such that a
n
>m−1/n for all n ≥1. On the
other hand, since the sequence a
n
is in A,wemusthavea
n
≤m for all n ≥1. Thus,
m −1/n < a
n
≤m.
It is easy to prove that m −1/n converges to m (it is also a consequence of the oper-
ations on limits to be proved in the next section). Hence, by the squeezing principle,
the sequence a
n
converges to m.
Exercises
1. (a) Let a
n
be a sequence of reals converging to .Letb
n
=a
n−1
. Show that b
n
converges to as well.
(b) State a generalization of the result in (a) and prove your claim.
2. Let 1 ≤j
1
<j
2
< ···<j
n
< ···be a sequence of natural numbers. Prove (by
induction) that j
n
≥n for all n ≥1.
3. (a) Show that if a
n
converges to a, then |a
n
| converges to |a| (use that ||x|−
|y||≤|x −y|).
(b) Is it true that if |a
n
| converges, then a
n
converges? Prove it or give a coun-
terexample.
4. (a) Assume that the real a is such that |a|<for any >0. Prove that a =0.
(b) Prove that a limit is unique (assume that a sequence a
n
has two limits a
and b, and show that |a −b|<for any >0.)
5. Assume that a
n
converges to a. Prove that for any >0, a
n
is in (a −,a +)
for all n except possibly finitely many.
6. Assume that a
n
converges to 1.
(a) Show that there is N such that if n ≥N , then a
n
< 2.

2.1 Sequences 39
(b) Show that there is N
1
such that if n ≥N
1
, then a
n
> 1/2.
7. Assume that the three sequences a
n
, b
n
, and c
n
are such that
a
n
≤b
n
≤c
n
for n ≥1000
and that the sequences a
n
and c
n
converge to the same limit . Explain how to
modify the proof of the squeezing principle so that the conclusion still holds.
8. Let A be a subset in the reals with a greatest lower bound k. Show that there
exists a sequence a
n
in A that converges to k.
9. Assume that a
n
is positive and converges to a limit .
(a) Assume that =0. Show that
√
a
n
converges to 0.
(b) Assume that >0. Show that
√
a
n
converges to
√
.
Write that
√
a
n
−
√
=
|a
n
−|
√
a
n
+
√
.
10. Let a
n
be a sequence of reals, and be a real. Let b
n
=|a
n
−|. Show that a
n
converges to if and only if b
n
converges to 0.
11. Assume that a
n
takes values in the set {0, 1, 2} for every n ≥1. That is, a
n
can
take only the values 0, 1, or 2. Suppose, moreover, that a
n
converges to 1. Show
that there is a natural N such that if n ≥N , then a
n
=1.
12. Consider a sequence a
n
that takes values in the naturals.
(a) Give an example of such a sequence.
(b) Show that a
n
converges if and only if it is stationary, that is, if and only if
there is a natural N such that if n ≥N , then a
n
=a
N
.
13. Consider the sequence a
n
=n
1/n
.Letb
n
=a
n
−1.
(a) Show that b
n
> 0forn ≥2.
(b) Show that
n =(b
n
+1)
n
≥
n(n −1)
2
b
2
n
.
(Use the binomial expansion
(a +b)
n
=
n
k=0
n
k
a
k
b
n−k
where all
n
k
are natural numbers and
n
2
=n(n −1)/2.)
(c) Use (a) and (b) to get
0 <b
n
≤
2
n −1
.
(d) Show that n
1/n
converges to 1.
14. (a) Assume that a
n
does not converge to a. Show that there exists an >0 and
a subsequence a
j
n
such that
|a
j
n
−a|> for all n.
(b) Let b
n
be a sequence of reals. Assume that there exists a b such that any
subsequence of b
n
has a further subsequence that converges to b. Show that
b
n
converges to b. (Do a proof by contradiction and use (a).)
