Schinazi R.B. From Calculus to Analysis
Подождите немного. Документ загружается.

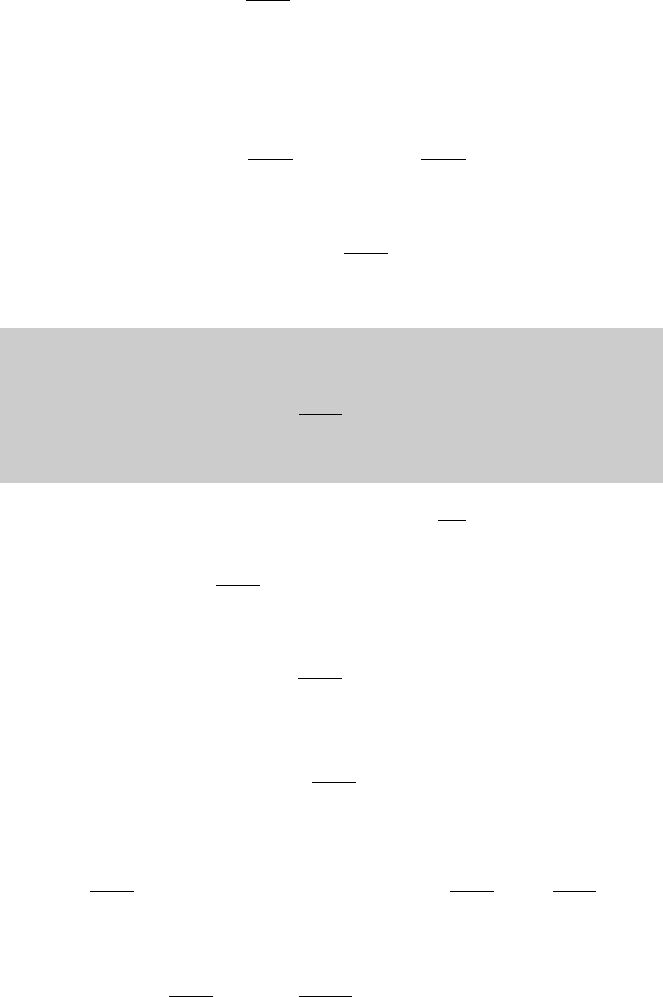
100 4 Fifty Ways to Estimate the Number π
where we use that
1
1 −x
≤1forx ≤0
and that
(−1)
n+1
x
n+1
≥0
for x ≤0 (why?). Thus,
−
y
0
x
n+1
1 −x
dx
≤(−1)
n+2
y
n+2
n +2
.
For fixed y in [−1, 0),
lim
n→∞
(−1)
n+2
y
n+2
n +2
=0.
We have completed the proof of the following power series expansion.
Power series expansion for ln(1 −x)
ln(1 −x) =−
∞
k=0
x
k+1
k +1
for all x ∈[−1, 1).
Application 4.3 Find a power series expansion for ln(
1+x
1−x
).
Observe first that
ln
1 +x
1 −x
=ln(1 +x) −ln(1 −x).
Since
ln(1 −x) =−
∞
k=0
x
k+1
k +1
for all x ∈[−1, 1),
if we let y =−x, we get
ln(1 +y) =
∞
k=0
(−1)
k
y
k+1
k +1
for all y ∈(−1, 1],
where we used that (−1)
k+2
=(−1)
k
. Subtracting the two power series, we get
ln
1 +x
1 −x
=ln(1 +x) −ln(1 −x) =
∞
k=0
(−1)
k
x
k+1
k +1
+
∞
k=0
x
k+1
k +1
.
The even powers cancel, and we get
ln
1 +x
1 −x
=2
∞
k=0
x
2k+1
2k +1
for all x ∈(−1, 1).
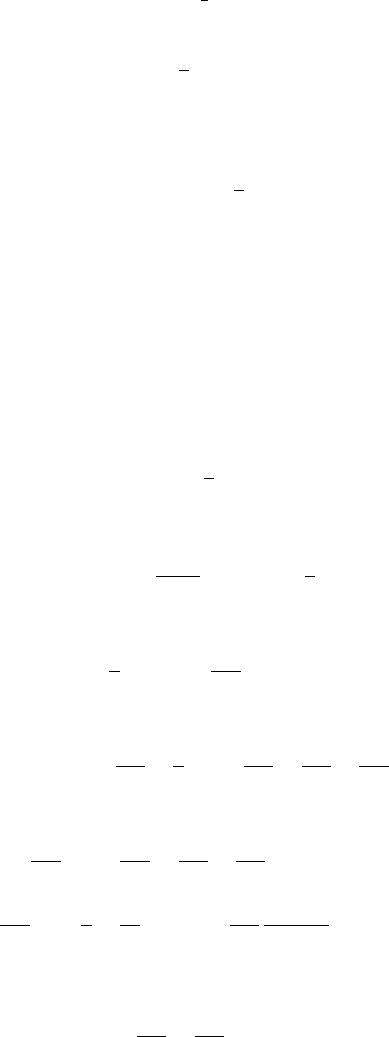
4.1 Power Series Expansions 101
Application 4.4 We know that the series
∞
k=1
1
k
diverges. In fact, since the partial
sum
S
n
=
n
k=1
1
k
is an increasing sequence and it does not converge, it must go to infinity. In this
application we will estimate how fast this happens. Define, for k ≥2,
a
k
=lnk −ln(k −1) −
1
k
.
Let
A
n
=
n
k=2
a
k
.
Note that
n
k=2
ln k −ln(k −1)
=lnn −ln 1 =ln n.
Hence,
A
n
=lnn −
n
k=2
1
k
.
We now show that A
n
converges. Observe that
ln n −ln(n −1) =−ln
n −1
n
=ln
1 −
1
n
.
Using the power series expansion for ln(1 −x) at x =1/n, we get
ln
1 −
1
n
=−
∞
k=1
1
kn
k
.
Hence,
a
n
=−ln(1 −1/n) −1/n =
k=1
1
kn
k
−
1
n
=
k=2
1
kn
k
=
1
2n
2
+
1
3n
3
+···.
We have
a
n
=
k=2
1
kn
k
<
k=2
1
2n
k
=
1
2n
2
+
1
2n
3
+···
=
1
2n
2
1 +
1
n
+
1
n
2
+···
=
1
2n
2
1
1 −1/n
,
where the last equality comes from the sum of a geometric series with ratio r =1/n.
On the other hand, it is clear that
a
n
=
k=2
1
kn
k
>
1
2n
2
.

102 4 Fifty Ways to Estimate the Number π
Hence,
1
2n
2
<a
n
<
1
2n
2
1
1 −1/n
.
By the squeezing principle we get
lim
n→∞
a
n
1/(2n
2
)
=1.
By the limit comparison test the series
n≥2
a
n
converges since
n≥1
1/(2n
2
) con-
verges. Therefore, the sequence
A
n
=lnn −
n
k=2
1
k
converges, and so
ln n −
n
k=1
1
k
converges as well (why?). The limit of this last sequence is called Euler’s constant.
In summary, ln n and
n
k=1
1
k
go to infinity at the same speed (very slowly).
Up to this point all the power series expansions we have considered were derived
from the geometric series. We now turn to a different method.
Binomial power series
Let α be a real number. Then, for all x in (−1, 1),
(1 +x)
α
=1 +
∞
k=1
α(α −1) ···(α −k +1)
k!
x
k
.
That is, for x in (−1, 1),wehave
(1 +x)
α
=1 +αx +α(α −1)
x
2
2!
+α(α −1)(α −2)
x
3
3!
+···.
In order to establish the binomial expansion, we use a differential equation. Let
f(x)=(1 +x)
α
for x ∈(−1, 1).
The function f is differentiable, and
f
(x) =α(1 +x)
α−1
.
Hence,
(1 +x)f
(x) =α(1 +x)
α
=αf (x).

4.1 Power Series Expansions 103
That is, f is a solution of the differential equation
(1 +x)h
(x) =αh(x) for all x ∈(−1, 1) and with h(0) =1. (E)
We now show that f is actually the unique solution of this differential equation. Let
k be another solution of (E) and define
h(x) =(1 +x)
−α
k(x).
Note that h is well defined on (−1, 1). Moreover, h is differentiable, and
h
(x) =−α(1 +x)
−α−1
k(x) +(1 +x)
−α
k
(x)
=(1 +x)
−α−1
−αk(x) +(1 +x)k
(x)
=0,
whereweusetheassumptionthatk is a solution of (E). Hence, h is a constant on
(−1, 1). Since h(0) =1, we have that h(x) =1 for all x in (−1, 1). That is,
k(x) =(1 +x)
α
for all x ∈(−1, 1).
This concludes the proof that there is a unique solution of (E).
We now need to show that the binomial power series is also a solution of (E). Let
S be defined by
S(x) =1 +
∞
k=1
α(α −1) ···(α −k +1)
k!
x
k
.
We first check that S is defined on (−1, 1).Fork ≥1, let
a
k
=
α(α −1) ···(α −k +1)
k!
x
k
.
We have
|a
k+1
|
|a
k
|
=
α(α −1) ···(α −k +1)(α −k)
α(α −1) ···(α −k +1)
k!
(k +1)!
|x|=
|α −k|
k +1
|x|,
which converges to |x| as k goes to infinity. By the ratio test the series converges for
|x|< 1. Hence, S is defined on (−1, 1). It turns out that power series are also dif-
ferentiable on any open interval on which they are defined. Moreover, the derivative
can be obtained by differentiating term by term. We will prove this result in Chap. 7.
Hence,
S
(x) =
∞
k=1
α(α −1) ···(α −k +1)
k!
kx
k−1
=
∞
k=1
α(α −1) ···(α −k +1)
(k −1)!
x
k−1
.
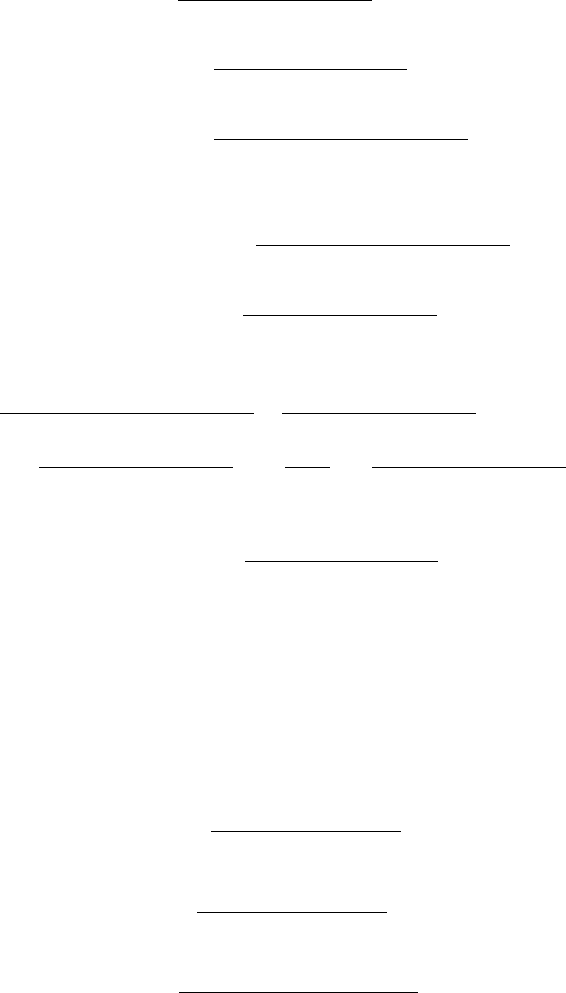
104 4 Fifty Ways to Estimate the Number π
We now compute (1 +x)S
(x) =S
(x) +xS
(x).Wehave
S
(x) =
∞
k=1
α(α −1) ···(α −k +1)
(k −1)!
x
k−1
=α +
∞
k=2
α(α −1) ···(α −k +1)
(k −1)!
x
k−1
=α +
∞
k=1
α(α −1) ···(α −k +1)(α −k)
k!
x
k
,
where the last equality comes from a shift of index. Therefore,
S
(x) +xS
(x) =α +
∞
k=1
α(α −1) ···(α −k +1)(α −k)
k!
x
k
+
∞
k=1
α(α −1) ···(α −k +1)
(k −1)!
x
k
.
Note that for all k ≥1, we have
α(α −1) ···(α −k +1)(α −k)
k!
+
α(α −1) ···(α −k +1)
(k −1)!
=
α(α −1) ···(α −k +1)
(k −1)!
1 +
α −k
k
=
α(α −1) ···(α −k +1)
k!
α.
Hence,
(1 +x)S
(x) =α +α
∞
k=1
α(α −1) ···(α −k +1)
k!
x
k
=αS(x).
Moreover, S(0) = 1. Therefore, S is the unique solution of (E). This proves that
S(x) =(1 +x)
α
and completes the proof of the binomial expansion.
Application 4.5 Consider the binomial series for α =n natural. We have
(1 +x)
n
=1 +
∞
k=1
a
k
x
k
with, for k ≥1,
a
k
=
n(n −1) ···(n −k +1)
k!
.
Note that
a
n
=
n(n −1) ···(n −n +1)
n!
=1
and that
a
n+1
=
n(n −1) ···(n −(n +1) +1)
(n +1)!
=0.

4.1 Power Series Expansions 105
Moreover, for all k>n, we will have a factor (n −n) in the numerator of a
k
. Hence,
a
k
= 0 for all k>n. That is, the binomial series in the particular case of a natural
exponent is a finite sum. We have
(1 +x)
n
=1 +
n
k=1
n(n −1) ···(n −k +1)
k!
x
k
for all x ∈R.
We will use a new notation to write this formula in a more convenient way. Note
that by multiplying by (n −k)! the numerator and denominator of a
k
we get
n(n −1) ···(n −k +1)(n −k)!
k!(n −k)!
=
n!
k!(n −k)!
.
The binomial coefficients are defined by
n
k
=
n!
k!(n −k)!
for 0 ≤k ≤n
that one reads: n choose k. Using the convention 0!=1, we get
n
0
=1.
Hence,
(1 +x)
n
=
n
k=0
n
k
x
k
for all x ∈R.
This is a well-known algebraic formula. See the exercises for a more general form
of this formula.
Application 4.6 Find the power series expansion of (1 +x)
−1/2
.
We use the binomial series expansion with α =−1/2. We have
(1 +x)
−1/2
=1 −
1
2
x +
−1
2
−3
2
x
2
2!
+
−1
2
−3
2
−5
2
x
3
3!
+···.
Define, for α =−1/2,
b
k
=α(α −1) ···(α −k +1).
We now show by induction that
b
k
=(−1)
k
(2k)!
2
2k
k!
for all k ≥1.
For k =1, the left-hand side is b
1
=α =−1/2, and the right-hand side is
(−1)
1
2!
2
2
1!
=
−1
2
.
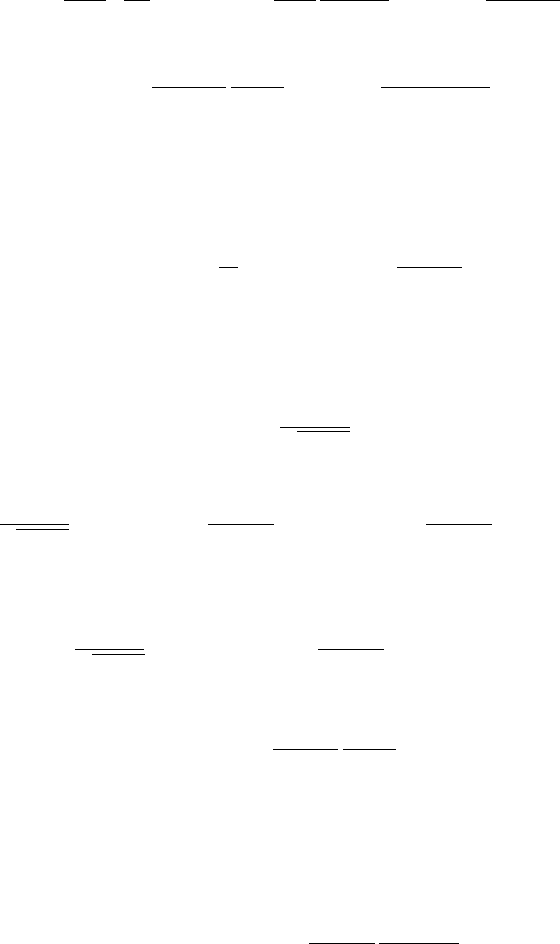
Hence, the formula holds for k =1. Assume that it holds for k. Then
b
k+1
=α(α −1) ···(α −k +1)(α −k) =(−1)
k
(2k)!
2
2k
k!
(α −k)
106 4 Fifty Ways to Estimate the Number π
by the induction hypothesis. We have
b
k+1
=(−1)
k
(2k)!
2
2k
k!
−1
2
−k
=(−1)
k
(2k)!
2
2k
k!
−2k −1
2
=(−1)
k+1
(2k +1)!
2
2k+1
k!
.
A little algebra yields
b
k+1
=(−1)
k+1
(2k +1)!
2
2k+1
k!
2k +2
2k +2
=(−1)
k+1
(2k +2)!
2
2k+2
(k +1)!
,
where we have used in the denominator that
2
2k+1
k!(2k +2) =2
2k+2
k!(k +1) =2
2k+2
(k +1)!.
This proves the formula by induction.
By the binomial series we have
(1 +x)
−1/2
=1 +
∞
k=1
b
k
k!
x
k
=1 +
∞
k=1
(−1)
k
(2k)!
2
2k
(k!)
2
x
k
for all x in (−1, 1).
Application 4.7 Find the power series expansion for arcsin. Recall that the deriva-
tive of arcsin is
(arcsin)
(x) =
1
√
1 −x
2
.
Substituting x by −x
2
into the power series expansion for (1 +x)
−1/2
, we get
1
√
1 −x
2
=1 +
∞
k=1
(−1)
k
(2k)!
2
2k
(k!)
2
−x
2
k
=1 +
∞
k=1
(2k)!
2
2k
(k!)
2
x
2k
for all x in (−1, 1). It is possible to integrate a power series by integrating it term
by term. This will be proved in Chap. 7. We use this property now. For y in (−1, 1),
y
0
1
√
1 −x
2
dy =
y
0
1 dy +
∞
k=1
(2k)!
2
2k
(k!)
2
y
0
x
2k
dy.
Since arcsin 0 =0, we have
arcsiny =y +
∞
k=1
(2k)!
2
2k
(k!)
2
y
2k+1
2k +1
for all y in (−1, 1).
Application 4.8 Use the power series expansion of arcsin to find an approximation
of π .
Recall that arcsin(1/2) =π/6. Hence,
π/6 =arcsin(1/2) =1/2 +
∞
k=1
(2k)!
2
2k
(k!)
2
(1/2)
2k+1
2k +1
.
In particular, if we sum up to k =10 (and multiply by 6), we get for π the approxi-
mation 3.141592647 for which the first seven decimals are correct.

4.1 Power Series Expansions 107
Exercises
1. Prove that for any real y,wehave
y
2n+2
1 +y
2
≤y
2n+2
.
2. Use the power series expansion of arctan at x =
1
√
3
to get the first 12 decimals
of π .
3. (a) Show that (−1)
n+2
y
n+2
n+2
is positive for y<0.
(b) Show that for fixed y ≤0,
lim
n→∞
(−1)
n+2
y
n+2
n +2
=0.
4. Assume that f and g have power series expansions
f(x)=
∞
n=0
a
n
x
n
,g(x)=
∞
n=0
b
n
x
n
for x in [0, 1].Letc and d be two reals. Show that cf +dg also has a power
series expansion on [0, 1].
5. Use the power series expansion of ln(1 −x) to estimate ln 2. Bound the error.
6. Show that
ln(1 −x) ≤−x
for all x in (0, 1).
7. Show that
1
1 −x
> 1 +x +x
2
for x in (0, 1).
8. If we approximate ln(1 −x) by −x −x
2
/2forx in (−1/2, 1/2), what is the
maximum error we are making?
9. (a) The power series expansion of ln(1 −x) is valid for x in [−1, 1). Explain
how it can be used to approximate ln y for any given y>0.
(b) Approximate ln 3. Find a bound for the error.
10. The genius Ramanujan (1887–1920) proposed the following formula:
1
π
=
√
8
9801
∞
n=0
(4n)!
(n!)
4
1103 +26390n
396
4n
.
Useittoestimateπ .
11. Estimate Euler’s constant (defined in Application 4.4). Bound the error.
12. Use Application 4.4 to show that
lim
n→∞
n
k=1
1
k
ln n
=1.
13. Recall that we say that a
n
goes to positive infinity if for any A, there is a natural
N such that a
n
>Afor n ≥N. Assume that a
n
and b
n
go to infinity.
108 4 Fifty Ways to Estimate the Number π
(a) Show that if a
n
−b
n
converges to a finite limit, then
lim
n→∞
a
n
b
n
=1.
(b) Is the converse of (a) true?
14. Use the formula in Application 4.5 to show that for all reals a and b and natu-
rals n,wehave
(a +b)
n
=
n
k=0
n
k
a
k
b
n−k
.
15. Use the binomial expansion to show that
1 −
√
1 −x =
∞
n=1
c
n
x
n
for |x|< 1, where
c
n
=
(2n −2)!
2
2n−1
n!(n −1)!
.
4.2 Wallis’ Integrals, Euler’s Formula, and Stirling’s Formula
For any integer n ≥0, let
I
n
=
π/2
0
sin
n
xdx.
The integrals I
n
are called Wallis’ integrals. Observe that
I
0
=
π/2
0
dx =π/2
and that
I
1
=
π/2
0
sin xdx=−cos(π/2) +1 =1.
For n ≥2, we use that sin
2
x =1 −cos
2
x to get
I
n
=
π/2
0
sin
n
xdx=
π/2
0
sin
n−2
(x)
1 −cos
2
x
dx.
Hence,
I
n
=I
n−2
−
π/2
0
sin
n−2
(x) cos
2
xdx. (4.2)
We now do a side computation. Recall from Calculus the integration-by-parts for-
mula: if f and g are differentiable on an interval [a,b] with continuous derivatives
on the same interval, then
b
a
f
(x)g(x) dx =f(b)g(b)−f(a)g(a) −
b
a
f(x)g
(x) dx.

4.2 Wallis’ Integrals, Euler’s Formula, and Stirling’s Formula 109
Letting f
(x) = sin
n−2
(x) cos x and f(x) =
1
n−1
sin
n−1
(x), g(x) = cos x and
g
(x) =−sin x, we get
π/2
0
sin
n−2
(x) cos
2
xdx=
1
n −1
sin
n−1
(π/2) cos(π/2) −sin
n−1
(0) cos(0)
−
π/2
0
1
n −1
sin
n−1
(x)(−sinx)dx =
I
n
n −1
.
Plugging
π/2
0
sin
n−2
(x) cos
2
xdx=
I
n
n −1
into (4.2), we get
I
n
=I
n−2
−
I
n
n −1
.
That is,
I
n
=
n −1
n
I
n−2
for n ≥2.
As shown below, this recursion formula can be used to compute any I
n
. Because the
recursion formula links I
n
to I
n−2
, we have different formulas for even n and odd n.
Wallis’ integrals
For any integer n ≥1, we have
I
2n+1
=
π/2
0
sin
2n+1
xdx=
2 ·4 ·6 ···2n
3 ·5 ·7 ···(2n +1)
and
I
2n
=
π/2
0
sin
2n
xdx=
1 ·3 ·5 ···(2n −1)
2 ·4 ·6 ···2n
π
2
.
We prove by induction that
I
2n+1
=
π/2
0
sin
2n+1
xdx=
2 ·4 ·6 ···2n
3 ·5 ·7 ···(2n +1)
.
The proof for the other formula is similar and is left as an exercise. We have already
computed I
1
=1. Since
I
n
=
n −1
n
I
n−2
,
we get
I
3
=
2
3
I
1
=
2
3
.
