Щербаков Б.Г., Попов А.А. Информационные технологии
Подождите немного. Документ загружается.


61
вероятность
поступления
двух
или
более
требований
одновременно
равна
нулю
или
имеет
столь
малую
величину
,
что
ею
можно
пренебречь
,
то
имеем
систему
с
ординарным
потоком
требований
.
Например
,
поток
требований
-
самолетов
,
поступающих
на
взлетно
-
посадочную
полосу
аэродрома
(
ВПП
), -
можно
считать
ординарным
,
так
как
вероятность
поступления
двух
и
более
самолетов
в
канал
обслуживания
(
ВПП
)
в
одно
и
то
же
время
очень
мала
и
ею
можно
пренебречь
.
3.
По
связи
между
требованиями
—
на
системы
без
последействия
от
поступивших
требований
и
с
последействием
.
Если
вероятность
поступления
требований
в
систему
в
некоторый
момент
времени
не
зависит
от
того
,
сколько
требований
уже
поступило
,
то
есть
не
связана
с
предысторией
изучаемого
процесса
,
то
мы
имеем
задачу
без
последействия
,
в
противном
случае
-
с
последействием
.
Примером
задачи
с
последействием
может
служить
поток
студентов
,
сдающих
зачет
преподавателю
.
4.
По
характеру
поведения
требования
-
в
системе
с
отказами
,
с
ограниченным
и
неограниченным
ожиданием
:
-
если
вновь
поступившее
требование
на
обслуживание
застает
все
каналы
обслуживания
уже
занятыми
и
покидает
систему
,
то
имеем
систему
с
отказами
.
Требование
может
выйти
из
системы
и
в
том
случае
,
когда
очередь
достигла
определенных
размеров
.
Если
ракета
противника
появляется
,
когда
все
противоракетные
установки
заняты
уничтожением
(
обслуживанием
)
других
ракет
,
то
она
благополучно
покидает
данную
область
;
-
если
поступившее
требование
застает
все
каналы
обслуживания
занятыми
и
становится
в
очередь
,
но
находится
в
ней
ограниченное
время
,
после
чего
,
не
дождавшись
обслуживания
,
покидает
систему
,
то
имеем
систему
с
ограниченным
ожиданием
.
Примером
такого
«
нетерпеливого
требования
»
может
быть
автосамосвал
с
раствором
.
Если
время
ожидания
велико
,
то
во
избежание
затвердения
раствора
он
может
быть
разгружен
в
другом
месте
;
-
если
поступившее
требование
,
застав
все
каналы
обслуживания
занятыми
,
вынуждено
ожидать
своей
очереди
до
тех
пор
,
пока
оно
не
будет
обслужено
,
то
имеем
систему
с
ожиданием
без
ограничения
.
Пример
:
самолет
,
который
находится
на
аэродроме
до
тех
пор
,
пока
не
освободится
взлетная
полоса
.
5.
По
способу
выбора
требований
на
обслуживание
-
с
приоритетом
,
по
мере
поступления
,
случайно
,
последний
обслуживается
первым
.
Иногда
в
таком
случае
говорят
о
дисциплине
обслуживания
:
-
если
система
массового
обслуживания
охватывает
несколько
категорий
требований
и
по
каким
-
либо
соображениям
необходим
определенный
подход
к
их
отбору
,
то
имеем
систему
с
приоритетом
.
Так
,
при
поступлении
изделий
на
стройплощадку
в
первую
очередь
монтируются
те
,
которые
необходимы
в
данный
момент
;
-
если
освободившийся
канал
обслуживает
требование
,
поступившее
в
систему
ранее
других
,
то
имеем
систему
с
обслуживанием
требований
по
мере
их
поступления
.
Это
наиболее
распространенный
класс
систем
.
Например
,
покупатель
,
подошедший
первым
к
продавцу
,
обслуживается
первым
.
Этот

62
способ
выбора
требований
на
обслуживание
применяется
там
,
где
в
силу
технических
,
технологических
или
организационных
условий
требования
не
могут
опережать
друг
друга
;
-
если
требования
из
очереди
в
канал
обслуживания
поступают
в
случайном
порядке
,
то
имеем
систему
со
случайным
выбором
требований
на
обслуживание
.
Пример
:
выбор
слесарем
-
сантехником
одной
из
нескольких
заявок
,
поступивших
от
жильцов
.
Выбор
здесь
,
как
правило
,
определяется
местоположением
самого
слесаря
:
он
выбирает
заявку
из
места
,
наиболее
близко
расположенного
к
нему
,
если
никакие
другие
факторы
не
влияют
на
выбор
;
-
последний
обслуживается
первым
.
Этот
способ
выбора
требований
на
обслуживание
используется
в
тех
случаях
,
когда
удобнее
или
экономнее
брать
на
обслуживание
требование
,
позже
всех
поступившее
в
систему
.
Так
,
при
укладке
строительных
изделий
в
штабель
удобнее
брать
из
штабеля
(
очере
ди
)
изделие
,
поступившее
последним
.
6.
По
характеру
обслуживания
требований
-
на
системы
с
детерминированным
и
случайным
временем
обслуживания
.
Если
интервал
времени
между
моментом
поступления
требования
в
канал
обслуживания
и
моментом
выхода
требования
из
этого
канала
постоянен
,
то
имеем
систему
с
детерминированным
временем
обслуживания
,
в
противном
случае
—
со
случайным
.
7.
По
числу
каналов
обслуживания
—
на
одноканальные
и
многоканальные
системы
.
Так
,
при
монтаже
дома
может
быть
использован
один
подъемный
кран
(
один
канал
обслуживания
)
или
несколько
(
много
каналов
)
для
обслуживания
прибывающих
на
стройку
изделий
.
8.
По
количеству
этапов
обслуживания
-
на
однофазные
и
многофазные
системы
.
Если
каналы
обслуживания
расположены
последовательно
и
они
неоднородны
,
так
как
выполняют
различные
операции
,
то
имеем
многофазную
систему
массового
обслуживания
.
Примером
такой
системы
может
служить
,
например
,
обслуживание
автомобилей
на
станции
техобслуживания
(
мойка
, '
диагностика
и
т
.
д
.).
9.
По
однородности
требований
,
поступающих
на
обслуживание
, -
на
системы
с
однородными
и
неоднородными
потоками
требований
.
Так
,
если
под
погрузку
прибывают
фургоны
одной
грузоподъемности
,
то
такие
требования
называются
однородными
,
в
противном
случае
-
неоднородными
.
10.
По
ограниченности
потока
требований
-
на
замкнутые
и
разомкнутые
системы
.
Если
поток
требований
ограничен
и
требования
,
покинувшие
систему
,
^
через
некоторое
время
в
нее
возвращаться
,
то
имеем
замкнутую
систему
,
в
противном
случае
-
разомкнутую
.
Примером
замкнутой
системы
может
служить
ремонтная
бригада
и
обслуживаемое
ею
оборудование
.
Если
изучены
или
заданы
входящие
потоки
требований
,
механизм
(
число
каналов
обслуживания
,
продолжительность
обслуживания
и
т
.
д
.)
и
дисциплина
обслуживания
,
то
это
дает
основание
для
построения
математической
модели
системы
.

63
Задачи
массового
обслуживания
условно
делят
на
задачи
анализа
и
синтеза
оптимизации
систем
массового
обслуживания
.
Первые
предполагают
определение
\
основных
параметров
функционирования
системы
массового
обслуживания
при
неизменных
,
наперед
заданных
исходных
характеристиках
:
структу
pa
системы
,
дисциплина
обслуживания
,
потоки
требований
и
законы
распределения
времени
на
их
обслуживание
.
Вторые
Направлены
на
поиск
оптимальных
параметров
систем
массового
обслуживания
.
§5.1 Функционирование системы массового обслуживания (СМО) в
установившемся режиме
Постановка задачи
Рассмотрим
одноканальную
замкнутую
систему
массового
обслуживания
(
СМО
)
с
неограниченным
временем
ожидания
требований
для
него
и
с
простейшим
потоком
.
Этот
поток
наиболее
полно
отвечает
реалиям
жизни
и
характеризуется
следующими
особенностями
:
•
поступление
требований
в
систему
на
обслуживание
происходит
по
одному
,
то
есть
вероятность
прибытия
двух
и
более
требований
одновременно
очень
мала
,
и
поэтому
ею
можно
пренебречь
(
поток
требований
ординарный
);
•
вероятность
поступления
последующих
требований
в
любое
время
не
зависит
от
возможности
их
прибытия
ранее
-
поток
требований
без
последействия
;
•
поток
требований
стационарный
.
Выявление основных особенностей, взаимосвязей и количественных
закономерностей
Функционирование
,
любой
системы
массового
обслуживания
можно
представить
через
все
возможные
ее
состояния
и
интенсивность
перехода
из
одного
состояния
в
другое
.
Основными
параметрами
функционирования
системы
массового
обслуживания
являются
вероятности
ее
состояния
,
то
есть
возможности
наличия
n
требований
(
покупателей
,
рабочих
,
заданий
,
машин
,
неполадок
)
в
системе
-(P
n.
Так
,
вероятность
Р
0
характеризует
состояние
,
когда
в
системе
нет
требований
и
"
канал
обслуживания
простаивает
.
Важным
параметром
функционирования
системы
массового
обслуживания
является
также
среднее
число
требований
,
находящихся
в
системе
N
CIICT
.
то
есть
в
очереди
на
обслуживание
и
средняя
длина
очереди
N
04
.
Исходными
параметрами
,
характеризующими
СМО
,
являются
:
число
каналов
обслуживания
N (
касс
,
компьютеров
,
кранов
,
ремонтных
бригад
);
число
требований
m (
покупателей
,
рабочих
,
заданий
,
машин
,
неполадок
),
интенсивность
поступления
одного
требования
на
обслуживание
λ
,
то
есть
число
поступлений
требований
в
единицу
времени
;
интенсивность
обслуживания
требований
µ
.
Интенсивность
поступления
требования
на
обслуживание
определяется
как
величина
,
обратная
времени
возвращения
требования
1
воз
:
64
Интенсивность
обслуживания
требований
определяется
как
величина
,
обратная
времени
обслуживания
одного
требования
- t
o6c
:
Решение задачи традиционными методами
Состояние
системы
массового
обслуживания
будем
связывать
с
числом
требований
,
находящихся
в
системе
:
•
в
системе
нет
ни
одного
требования
-
вероятность
состояния
Р
0
; ' \
•
в
системе
находится
одно
требование
-
вероятность
состояния
Р
.;
!
ч
•
в
системе
находится
п
требований
-
вероятность
состояния
Р
п
. )
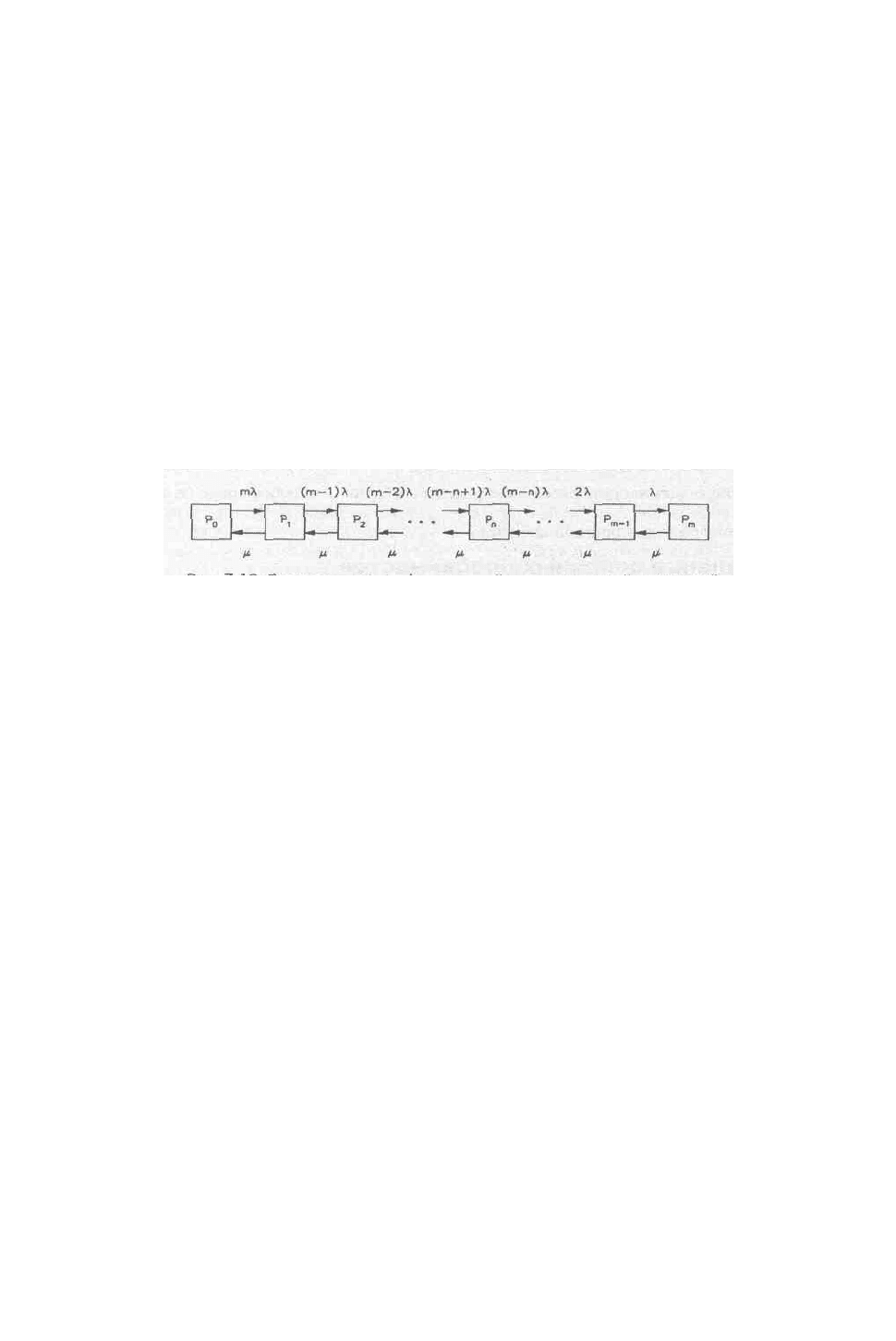
Представим
все
возможные
состояния
СМО
в
виде
размеченного
графа
состояний
(
рис
. 5.1.1).
Каждый
прямоугольник
графа
,
количественно
оцениваемый
вероятностью
состояний
Р
п
,
определяет
одно
из
всех
возможных
состояний
.
Стрелки
указывают
,
в
какое
состояние
система
может
перейти
и
с
какой
интенсивностью
.
Рис
. 5.1.1.
Размеченный
граф
состояний
одноканальной
замкнутой
системы
массового
обслуживания
Первый
прямоугольник
с
вероятностью
Р
0
определяет
состояние
системы
массового
обслуживания
,
при
котором
канал
обслуживания
простаивает
из
-
за
отсутствия
требований
в
ней
.
Из
этого
положения
система
массового
обслуживания
может
перейти
с
интенсивностью
m
λ
только
в
состояние
Р
1 ;
тогда
в
системе
появится
одно
требование
,
так
как
входной
поток
-
ординарный
.
С
интенсивностью
µ
система
может
перейти
также
из
состояния
Р
1
в
состояние
Р
0
;
когда
в
системе
находилось
одно
требование
,
но
оно
было
обслужено
раньше
,
чем
появилось
новое
.
Из
состояния
Р
1
система
массового
обслуживания
может
перейти
с
интенсивностью
(m - 1)
λ
в
состояние
Р
2
;
тогда
в
системе
появятся
два
требования
.
С
интенсивностью
µ
система
может
перейти
также
из
состояния
Р
2
в
состояние
Р
1;
когда
в
системе
находилось
два
требования
,
но
одно
из
них
было
обслужено
раньше
,
чем
появилось
новое
,
и
т
.
д
.
Рассмотрим
установившийся
режим
работы
системы
массового
обслуживания
,
когда
основные
вероятностные
характеристики
ее
постоянны
во
времени
,
например
в
течение
часа
.
В
этом
случае
интенсивности
входных
и
выходных
потоков
для
каждого
состояния
будут
сбалансированы
:
P
0
m
λ
=P
1
µ
P
1
(
µ
+(m-1)
λ
)= P
0
m
λ
+ P
2
µ
P
2
(
µ
+(m-2)
λ
) = P
1
(m-1)
λ
+ P
3
µ
………………………………
P
n
(
µ
+(m-n)
λ
) = P
n-1
(m-(n-1))
λ
+ P
n+1
µ

65
…………………….
P
m
µ
=P
m-1
λ
Обозначим
величину
λ
/m
через
ψ
и
назовем
ее
коэффициентом
загрузки
.
Из
первого
уравнения
можно
найти
значение
Р
1
:
P
1
=P
m
λ
/
µ
=P
0
m
ψ
Из
второго
уравнения
найдем
значение
Р
2
:
P
2
=P
1
+P
1
(m-1)
λ
/
µ
–P
0
m
λ
/
µ
Но
первый
член
–
Р
1
=
Р
0
m
λ
/
µ
,
следовательно
,
первый
и
третий
сокращаются
:
Р
2
=
Р
1
(m- 1)
λ
/
µ
=
Р
о
m(m - 1)
ψ
2
.
Из
третьего
уравнения
найдем
значение
Р
3
:
Р
3
=
Р
2
+
Р
2
(m - 2)
λ
/
µ
–
Р
1
(m - 1)
λ
/
µ
Но
первый
член
-
Р
2
=
Р
1
(m - 1)
λ
/
µ
,
следовательно
,
первый
и
третий
сокращаются
:
Р
3
=
Р
2
(m - 2)
λ
/
µ
=
Р
0
m (m - 1)(m - 2)
ψ
3
и
т
.
д
.;
Р
n
=
Р
n-1
(m - (n - 1))
λ
/
µ
= P
0
m (m - 1)...(m - (n - 1))
ψ
n
= P
0
ψ
n
(m!/(m-n)!
Используя
очевидное
равенство
ΣР
п
= 1,
получим
: 1 = P
Q
Σψ
n
m!/(m-n)!
от
n = 0
до
m.
Зная
вероятность
простоя
канала
обслуживания
Р
0
,
можно
определить
его
фактическую
производительность
:
P
f
=(l-P
0
)
µ
G,
где
G,
например
,
количество
груза
,
помещенного
за
одно
обслуживание
в
машину
.
Для
установившегося
режима
работы
системы
средняя
интенсивность
поступления
требований
во
входном
потоке
равна
аналогичной
характеристике
выхода
требований
из
канала
обслуживания
:
(m-N
сист
)
λ
= (l-P
0
)
µ
,
где
N
сист
-
среднее
число
обслуживаемых
требований
,
находящихся
в
системе
.
Из
данного
равенства
можно
легко
найти
среднее
число
требований
(
покупателей
,
рабочих
,
заданий
,
машин
,
неполадок
),
находящихся
в
системе
N
CIICT
:
N
сист
= m-(l-P
0
)/
ψ
.
Среднее
же
число
требований
(
машин
),
находящихся
в
очереди
,
будет
вычислено
так
:
N
oч
-
-
N
CHCT
- (1 –
Р
0
) = m - (1 - P
0
)(1/
ψ
+ 1).
Пусть
задан
комплект
машин
«
экскаватор
-
автосамосвалы
».
Экскаватор
погружает
за
один
рабочий
цикл
g
a
= 1
т
грунта
.
Грузоподъемность
автосамосвала
g
a
= 7
т
.
Число
машин
,
обслуживающих
экскаватор
, m = 5.
Время
рабочего
цикла
экскаватора
составляет
t
рц
= 18
с
,
а
время
обращения
автосамосвала
t
обр
= 10
мин
.
Тогда
время
погрузки
одного
грузовика
составит
:
t
пог
=
Интенсивность
погрузки
автосамосвала
экскаватором
составит
29
погрузок
в
час
.
Интенсивность
же
поступления
автосамосвала
на
погрузку
составит
6
обращении
в
час
.

66
t-
воз
1"
Коэффициент
ψ
=
λ
/
µ
будет
равен
ψ
= 0,207.
Вероятность
простоя
экскаватора
в
этом
случае
составит
:
Таким
образом
,
фактическая
производительность
данного
комплекта
машин
будет
на
27,1%
ниже
технической
.
Вероятности
наличия
n
машин
в
системе
:
Р
1
=
Р
0
m
ψ
= 0,281
Р
2
=
Р
1
(m - 1)
ψ
= 0,233
Р
3
=
Р
2
(m-2)
ψ
= 0,144
Р
4
=
Р
3
(m - 3)
ψ
= 0,06
Р
5
=
Р
4
(m-4)
ψ
= 0,012 ;,
Фактическая
производительность
комплекта
машин
:
P
f
- (1 -
Р
„)
µ
G = (1 - 0,271) X 29 X 7 = 147,947
т
/
час
.
Среднее
число
машин
,
находящихся
в
системе
:
N
сист
= m-(l-P
0
)/
ψ
= 1,477.
Среднее
число
машин
,
находящихся
в
очереди
:
N
o
4
- N
CИCT
- (1 -
Р
0
) = m - (1 -
Р
0
) (1 /
ψ
+ 1) = 0,749.
Решение задачи с использованием системы Mathcad
Ввод
текста
на
всех
этапах
решения
задачи
будем
осуществлять
с
помощью
комбинации
клавиш
Shift+" (
двойная
кавычка
),
что
позволит
создать
текстовую
область
.
Введем
на
рабочем
листе
первый
пункт
расчета
(
рис
. 5.1.2).
Он
будет
выглядеть
так
:
1.
Задание
исходных
данных
одноканальной
замкнутой
СМО
.
Последовательно
введем
исходные
данные
:
-
интенсивность
обслуживания
требований
µ
: = 29;
-
интенсивность
поступления
одного
требования
на
обслуживание
λ
: = 6;
-
число
требований
,
функционирующих
в
системе
, m: = 5.
Для
решения
задачи
воспользуемся
блоком
функций
Given ... Find.
Его
применение
требует
предварительного
задания
начальных
приближений
.
Введем
на
рабочем
листе
второй
пункт
расчета
(
рис
. 5.1.2).
Он
будет
выглядеть
так
:
2.
Начальные
приближения
.
Последовательно
наберем
начальные
приближенные
значения
искомых
параметров
:
Р
0
:=0,25
Р
.:-0,15
Р
2
:=0,15
Р
3
:-0,15
Р
4
:=
ОД
5
Р
5
:=0,15
Сумма
вероятностей
всех
состояний
должна
быть
равна
1.
Введем
на
рабочем
листе
третий
пункт
расчета
(
рис
. 5.1.2).
Он
будет
выглядеть
так
:
3.
Запись
системы
уравнений
,
описывающей
функционирование
одноканалъной
СМО
.
Вначале
записывается
ключевое
слово
Given
(
Дано
),

67
которое
может
быть
напечатано
прописными
,
строчными
буквами
или
начинаться
с
прописной
.
Рис
5.1.2.
Определение
параметров
функционирования
одноканальной
замкнутой
СМО
в
системе
Mathcad
Ниже
вводится
исходная
система
уравнений
.
Для
примера
ограничимся
рассмотрением
одноканальной
замкнутой
системы
,
в
которой
обслуживаются
пять
требований
.
Интенсивность
поступления
одного
требования
на
обслуживание
λ
равна
трем
поступлениям
в
час
.
Интенсивность
обслуживания
в
канале
µ
составляет
29
обслуживании
в
час
.
Эта
система
алгебраических
уравнений
будет
выглядеть
так
:
P
0
m
λ
=P
1
µ
P
1
(
µ
+(m-1)
λ
)= P
0
m
λ
+ P
2
µ
P
2
(
µ
+(m-2)
λ
) = P
1
(m-1)
λ
+ P
3
µ
………………………………
P
4
(
µ
+(m-4)
λ
) = P
3
(m-3)
λ
+ P
5
µ
P
5
µ
=P
4
λ
Однако
в
представленном
виде
определитель
системы
будет
равен
нулю
-
система
вырождена
Во
избежание
этой
ситуации
заменим
последнее
выражение
следующим
равенством
:
P
0
+P
1
+P
2
+P
3
+P
4
+P
5
=1
В
заключение
вводится
вектор
искомых
величин
.
Для
этого
в
поле
рабочего
листа
(
рис
. 5.1.2)
определим
местоположение
вектора
,
который
должен
находится
несколько
ниже
системы
равенств
.
Если
в
окне
имеется
панель
инструментов
Math (
Математика
),
щелкнем
по
кнопке
с
изображением
матрицы
.
Появится
окно
Matrix
(
Матрица
),
далее
-
по
кнопке
с
аналогичным
изображением
или
воспользуемся
комбинацией
клавиш
Ctrl+M
.
В
обоих

68
случаях
появится
диалоговое
окно
Insert Matrix
(
Вставить
матрицу
).
В
текстовых
полях
Rows
(
Строки
)
и
Columns
(
Столбцы
)
этого
диалогового
окна
вставляем
нужное
число
строк
и
столбцов
,
в
нашей
задаче
- 6
и
1
соответственно
.
После
щелчка
по
клавише
ОК
появится
шаблон
с
метками
для
ввода
искомых
параметров
(
Р
0
,
Р
1
,
Р
2
,
Р
3
,
Р
4
,
Р
5
).
Осуществим
эту
операцию
,
подведя
курсор
или
указатель
мыши
к
каждой
метке
.
Затем
произведем
ввод
знака
присваивания
и
имени
встроенной
функции
Find(P
0
,P
1
,P
2
,P
3
,P
4
,P
5
).
Введем
на
рабочем
листе
четвертый
пункт
расчета
(
рис
. 5.1.2).
Он
будет
выглядеть
так
: 4.
4
Результаты
решения
.
Для
получения
результатов
расчета
искомых
величин
достаточно
набрать
имя
нужного
параметра
и
знак
равенства
,
нажав
соответствующую
клавишу
или
щелкнув
по
кнопке
со
знаком
равенства
,
расположенной
в
верхнем
левом
углу
панели
инструментов
Evalu... (
Вычисления
).
Анализируя
полученные
результаты
решения
в
системе
Mathcad,
можно
заметить
,
что
значения
для
параметров
Р
0
,
Р
.,
Р
2
,
Р
3
,
Р
4
,
Р
5
совпадают
с
соответствующими
значениями
,
полученными
вручную
.
§5.2 Функционирование системы массового обслуживания (СМО) в
неустановившемся режиме
Рассмотрим
неустановившийся
режим
работы
системы
массового
обслуживания
,
когда
основные
вероятностные
характеристики
ее
зависят
от
некоторого
промежутка
времени
.
В
этом
случае
интенсивности
входных
и
выходных
потоков
для
каждого
состояния
будут
сбалансированы
,
но
уже
с
учетом
производных
вероятностей
.
Таким
образом
,
мы
будем
иметь
систему
обыкновенных
дифференциальных
уравнений
,
описывающих
функционирование
одноканальной
замкнутой
системы
при
неустановившемся
режиме
.
Для
составления
системы
обыкновенных
дифференциальных
уравнений
,
описывающей
функционирование
СМО
с
пуассоновским
потоком
,
существует
мнемоническое
правило
:
•
производная
dP
n
(t)/dt
вероятности
пребывания
системы
в
состоянии
п
равна
алгебраической
сумме
нескольких
членов
;
•
число
членов
этой
суммы
равно
числу
стрелок
на
графе
состояний
системы
,
соединяющих
состояние
n
с
другими
;
•
если
стрелка
направлена
в
рассматриваемое
состояние
n,
то
член
берется
со
знаком
«
плюс
»;
•
если
стрелка
направлена
из
рассматриваемого
состояния
n,
то
член
берется
со
знаком
«
минус
»;
•
каждый
член
суммы
равен
произведению
вероятности
того
состояния
,
из
которого
направлена
стрелка
,
на
интенсивность
потока
событий
,
переводящего
систему
по
данной
стрелке
.
В
соответствии
с
размеченным
графом
состояний
(
рис
. 5.1.1)
эта
система
обыкновенных
дифференциальных
уравнений
будет
выглядеть
так
:
dP
0
(t)/dt = P
1
(t)
µ
- P
0
(t)m
λ

69
dP
1
(t)/dt = P
0
(t) m
λ
+ P
2
(t)
µ
– P
1
(t)(
µ
+(m-1)
λ
)
dP
2
(t)/dt = P
1
(t) (m - 1)
λ
+ P
3
(t)
µ
- P
2
(t) (
µ
+ (m - 2) 1)
…………………………….
dP
n
(t)/dt = P
n
.
1
(t)(m-(n - 1))
λ
+ P
n+1
(t)
µ
- P
n
(t) (
µ
+ (m - n)
λ
)
…………………………….
dP
m
(t)/dt = P
m
.
1
(t)
λ
-P
m
(t)
µ
Как
можно
заметить
,
требуется
большая
вычислительная
работа
для
определения
основных
параметров
функционирования
комплекта
машин
.
Можно
пойти
тремя
путями
.
Первый
-
предварительный
расчет
Р
0
для
различных
значений
коэффициента
использования
ψ
(
табл
. 5.2.1).
Второй
-
применение
какого
-
либо
языка
высокого
уровня
для
решения
этой
задачи
.
Третий
-
использование
системы
Mathcad.
Таблица
5.2.1
Число
требование
.,
обслуживаемых
системой
, —
т
Коэф
.
загр
.,
2
3
4
5
6
7
Вероятность
простоя
канала
обслужи
5
ания
,
Р
О
0.04
0.9232
0.8850
0.8469
0.8090
0.7712
0.7334
0.06
0.8872
0.8313
0.7760
0,7212
0.6670
0.6134
0.08
0.8527
0.7804
0.7092
0.6394
0.5712
0.5049
0.10
0.8197
0.7321
0.6467
0.5640
0.4845
0.4090
0.12
07881
0.6865
0.5885
0.4952
0.4075
0.3266
0.14
0.7580
0.6435
0.5347
0.4331
0.3602
0.2577
0.16
0.7293
0.6031
0.4851
0.3775
0.2822
0.2013
0.18
0.7019
0.5652
0.4398
0.3282
0.2331
0.1561
0.20
0.6757
0.5297
0.3983
0.2849
0.1918
0.1205
Рассмотрим
неустановившийся
режим
работы
системы
массового
обслуживания
,
когда
ее
основные
вероятностные
характеристики
зависят
от
времени
,
например
в
течение
0,3
часа
.
В
этом
случае
интенсивности
входных
и
70
выходных
потоков
для
каждого
состояния
будут
сбалансированы
,
но
уже
с
учетом
производных
вероятностей
.
Таким
образом
,
мы
будем
иметь
систему
обыкновенных
дифференциальных
уравнений
,
описывающих
функционирование
одноканальной
замкнутой
системы
при
неустановившемся
режиме
.
Для
примера
ограничимся
рассмотрением
той
же
самой
системы
,
в
которой
обслуживаются
пять
требований
.
Интенсивность
поступления
одного
требования
на
обслуживание
X
равна
трем
поступлениям
в
час
.
Интенсивность
обслуживания
в
канале
ц
составляет
29
требований
в
час
.
Эта
система
обыкновенных
дифференциальных
уравнений
будет
выглядеть
так
:
dP
0
(t)/dt = P
1
(t)
µ
- P
0
(t)m
λ
dP
1
(t)/dt = P
0
(t) m
λ
+ P
2
(t)
µ
– P
1
(t)(
µ
+(m-1)
λ
)
dP
2
(t)/dt = P
1
(t) (m - 1)
λ
+ P
3
(t)
µ
- P
2
(t) (
µ
+ (m - 2) 1)
…………………………….
dP
4
(t)/dt = P
3
(t)(m-3))
λ
+ P
5
(t)
µ
– P
4
(t) (
µ
+ (m - 4)
λ
)
dP
5
(t)/dt = P
4
(t)
λ
-P
5
(t)
µ
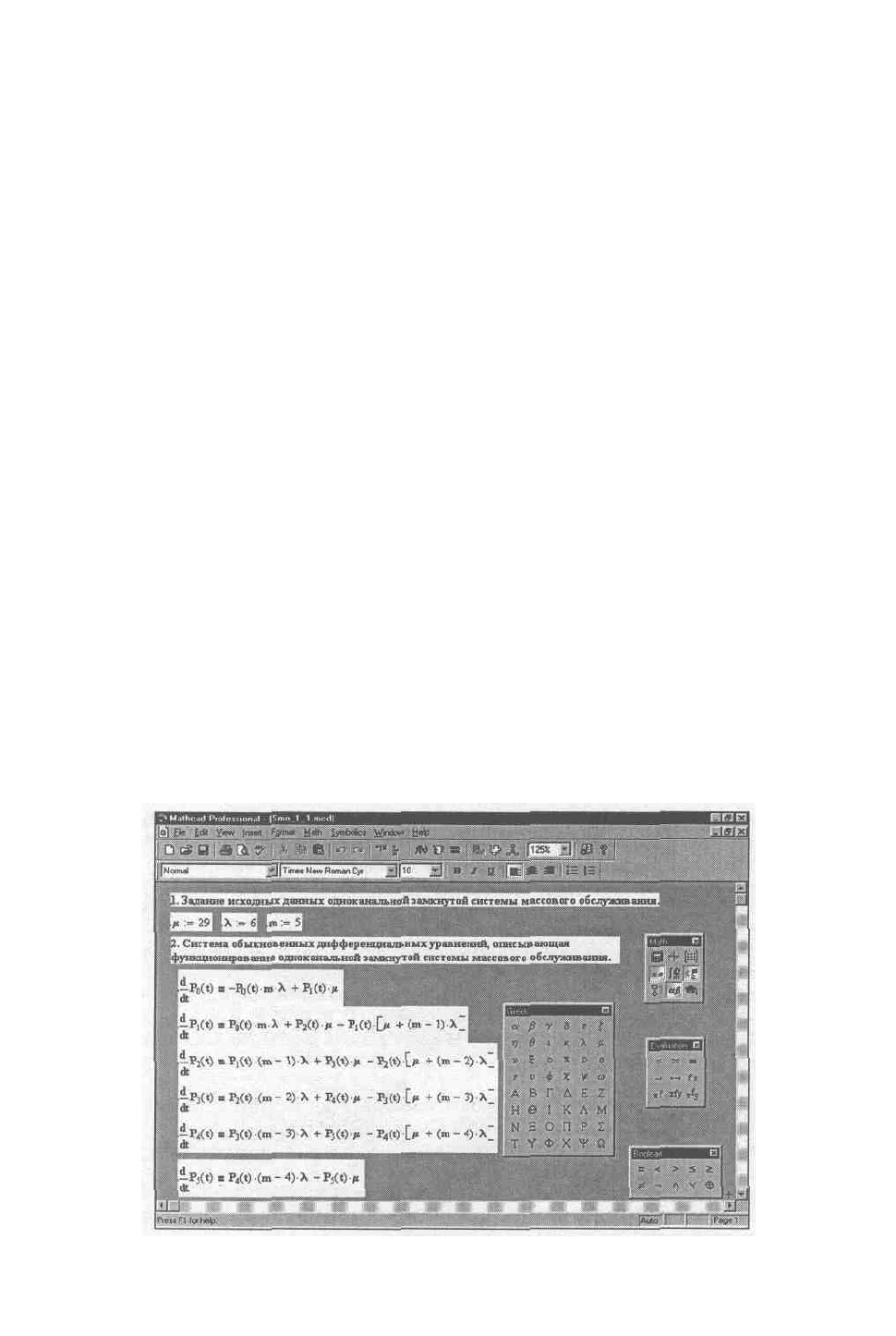
На
рис
. 5.2.1
представлены
начальные
исходные
данные
и
система
дифференциальных
уравнений
,
описывающая
функционирование
одноканальной
замкнутой
СМО
при
неустановившемся
режиме
работы
На
рис
5.2.2
система
дифференциальных
уравнений
представлена
в
доступном
для
решения
виде
в
системе
Mathcad.
Здесь
изображены
правые
части
системы
дифференциальных
уравнений
в
форме
вектора
-
столбца
,
каждый
элемент
которого
определяет
значение
правой
части
соответствующего
уравнения
на
каждом
шаге
интегрирования
(
решения
),
и
даны
начальные
значения
искомых
параметров
тоже
в
виде
вектора
-
столбца
В
нижней
части
рисунка
определены
начальное
и
конечное
время
интегрирования
и
число
шагов
решения
системы
дифференциальных
уравнений
.
Рис
5.2.1
Описание
функционирования
одноканальной
замкнутой
системы
массового
обслуживания
при
неустановившемся
режиме
