Scheideler C. Universal Routing Strategies for Interconnection Networks

Подождите немного. Документ загружается.

12.5 Proof of Theorem 12.3.2 201

r t_>log l+log 7~ ,

where

7 = 32B(A+L(9

. Since C _> 2 l~ 5~-~, the expected runtime of the

protocol is at least

~2(L--CB +(r ).

Since this bound gets minimal for/~ = O(L@ - + D + L), we get an expected

runtime of at least

time steps, where a = C + B( D + 1) + 2 and fl =

a/C + 2.

12.5 Proof of Theorem 12.3.2

In this section we prove upper and lower bounds on the runtime of our proto-

col for shortcut-free path collections using serve-first routers. Hence suppose

we want to route worms of length L along a collection of n shortcut-free

paths with path congestion C and dilation D, using serve-first routers with

bandwidth B. (We again assume that C covers both messages and acknowl-

edgments.)

12.5.1 The Upper Bound

In this section we prove the upper bound in Theorem 12.3.2. Let the witness

tree

W(t)

be defined as in Section 12.4. For any valid embedding ~a into

W(t),

let

= [Vii denote the total number of worms and

gi = mi - mi-t

denote

the number of new worms at level i. Furthermore let

denote the number

of old worms that axe in a connected component in

with a new worm.

Let Cj be an upper bound for the path congestion that holds w.h.p, after

round j using the trial-and-failure protocol for suitably chosen A1,..., Aj

(determined later). Then it holds for the number

V(t, k)

of valid embeddings

in ~;(t) using k worms:

t mi-t

tl ..... it>o, i=1

ci=s ~i

El s

0[~/+ 1 " (ti "{-

Ci) ci-s

(~'ni--1 -- C{) mi-l-ci ,

w.h.p. This formula is derived as follows.

202 12. Protocols for All-Optical Networks

There are n ways to choose the worm that is embedded in the root of )4)(t).

There are ( c, ) possibilities to choose

old worms that lie in a connected

component in Gi with a new worm, and (~:) possibilities to choose

old

worms that collide with (and therefore narrow down the choices for) each

~gl

of the

new worms. Therefore afterwards there are at most

C~_i+ 1

ways

w.h.p, to choose the g~ new worms. For the remaining

ci - gi

old worms

there are at most

gi + ci

possibilities to choose the worm that prevents it

from moving forward.

For each of the remaining

mi-1 - ci

old worms there are at most m~-i -

ways to determine the old worm which prevents it from moving forward.

Before we can proceed with our calculation, we need an upper bound

that holds for the path congestion w.h.p., and need an upper bound for the

probability that the embeddings counted in

V(t, k)

are active.

Since the delays and wavelengths are chosen independently and we only

consider shortcut-free paths, it holds for every pair of worms wi and wj at

round t that

Pr[wi is blocked by wj] < BA----~

Therefore we get analogous to Lemma 12.4.2 that, if Ai >_ 4eB--V:f for

all i E {1,...,t- 1}, then the path congestion Ct at round t is at most

max{ 2,c_1, O(log n)}, w.h.p.

Next we bound the probability that the embeddings counted in

V(t, k)

are active. As noted above, the probability that a collision pair

(w,w')

level i of Yl;(t) is active is at most L For every level i, each connected

BAt_~+ a 9

component in G~ that contains no new worms has a size of at least three.

This is true since we only allow the worms to be routed along shortcut-free

paths and therefore two worms can not block each other. Hence there are

at most gi ~ m~ components with no new worms. Since every connected

component of size s implies a probability of at most

t n~s-1

that its

BAt-~+I j

edges represent collisions of worms we obtain a probability of at most

2(mi_l--C I )

BAt_i+ 1 - B A-~_I+ 1

that these components are active. Note that we can improve this bound if

we know that at least k > 3 pieces of paths in the collection axe needed to

obtain a directed cycle in Gi.

According to Section 12.4, each connected component in

that contains

a new worm forms a tree. Furthermore each new worm lies in a different

connected component. Therefore the probability that their edges represent

collisions of worms is at most

Bz~i+l )

12.5 Proof of Theorem 12.3.2 203

Altogether the probability that all collision pairs in level i are active given

mi-1 and ci

is at most

L ~ c,+ 2(-,,~1-o,)

BA~-i+I ]

Therefore the probability

P(t, k)

that there exists an active embedding in

~4}(t) is at most

s .... s >0, i=1

Ci=~i \ Ci ] \ I/

Ei s

2(rnz-- 1 --ei)

(mi-a-

Ci) m'-x-c' ( L .c,+\

\ BAt-i+l ]

In order to simplify this formula, we have to distinguish between two cases.

s < ci/2

we get

and otherwise

eci ~ci-ti [3cAC~-tl

\ci-ti] ~2 ~J

<_ (3eci) c'-t' ,

c~) (ei + c~) c'-t'

< 89 (2c~)c,-t,

Let Ai _> ~ for all i 9 {1,..., t). Then it holds

-- 2(mi -- 1 -- r )

ci=l, \

Ci "/ i+l

<_ m,_, \mi-lemi--1-- ci]~m'-x-c'

(Ci)(~i_~ci)ci_s

-- Ci)ml-x--Cl "

2(m~--X--C i )

B At-i+ i ]

< (emi_,) 'm-x-ti \BAt_i+1/

m'-l(ei)(gi+ci)C'-t'(l gi \emi------~] BAt-i+IL )~

Ci=ti

2(mi_ x --ti)

< (erni_l) m'-x-~'

BA~i+I

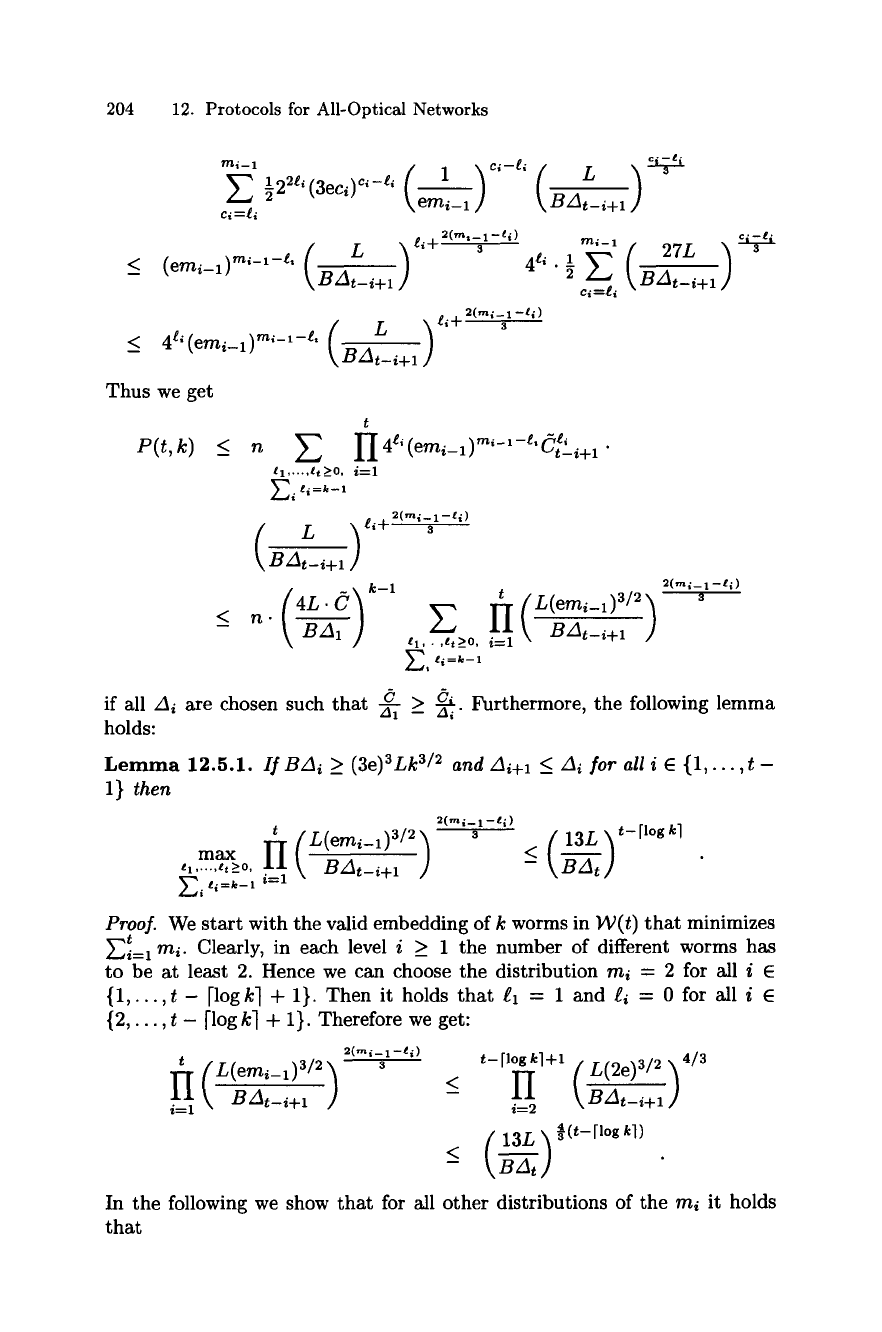
204 12. Protocols for All-Optical Networks

c i-t i

E 89 22~'(3eci)c'-~'(

1 ,~e~-tl L 3

Ci=e i

\ emi-------~ ] B z3t-i+ l

<- (emi-1)m'-'-t' BAZi+I

4t''89 Z

\BAt_i+1/

Ci=tl

ti+ 2(ml-- l --ti)

_< 4t'(emi_l) 'm-'-t' BAt_i+ 1

Thus we get

P(t,k) < n ~_, II 4t'(emi-~)m'-~-t'd['--i+~ "

ll ..... lt_>0, i=1

Ei gi=k--1

2(mi_ 1 --li)

BAT-i+I

9

(4L.~ k-1 t (L(emi_l)3/2)

tl,.,tt>_o, i=1

2(rni_ 1 --ti)

c i-Q

t (L(emi_l)3/2)

H \ BA~_~+I

i=1

2(ml-- 1 --ti)

t-[logkl+X ( L(2e)3/2 ~ 4/3

< II \BAt_~+I]

i=2

( 13L h

In the following we show that for all other distributions of the mi it holds

that

{2,..., t - [log k] + 1}. Therefore we get:

if all Ai are chosen such that 0 > O/ Furthermore, the following lemma

ZT1

zai"

holds:

Lemma

12.5.1.

If BAi >_ (3e)3Lk 3/2 and Ai+l <_ Ai for all i E

{1,...,t--

then

t (L(emi_l)3/2)2(m,_~,-e,!

( 13L ~'-['~

max H \ BAt_i+ 1 < kBAt]

t 1 ..... tt>_O,

Ei timk-1 i=1

Proof.

We start with the valid embedding of k worms in W(t) that minimizes

~i=1

mi.

Clearly, in each level i > 1 the number of different worms has

to be at least 2. Hence we can choose the distribution

= 2 for all i E

{1,...,t - [logk] + 1}. Then it holds that s = 1 and ~i = 0 for all i E

12.5 Proof of Theorem 12.3.2 205

t (L(emi_l)312,~2("'~ '-'')

( 13L'~

l(, -r,ogVl)

< (12.7)

9 = t,,

BAt-i+l

,,] - \B-~-tt]

BAi > (3e)3Lk 3/2.

Consider increasing the number mj of worms at a stage j < t with m s <

mj+l by 1. Then two terms in the product in (12.7) change: the (i = j)-term

and the (i = j + 1)-term. Before increasing ms, these terms are

2(,~i_ 1 -t j)

2(,- i-ti+l)

(

L(ems_l)3/2 ~ s [L(ems)3/2 s

BAt-j+1 ] ~ BAt-j ]

and after increasing m s by 1, they change to

2(,,~i_ ~ -(ti+l)) 2((,~i+l)-(tj+ 1-1))

(

L(ems_l)3/2, I 3 (L(e(ms + l))3/2~ s

BAt-s+I ] \ BAt-s ]

It holds

(12.8) > (12.9)

(12.8)

. (12.9)

( L(emj_l )3/2 ~

2/3

\ BAt-s+I ) >

ms +l~me-G+' (L(e(ms +1))3/2 4/3

(L(ems_l)3/2"~ 2/3 (L(e(2ms-1 +

I))3/2'~ 4/3

BA,-s+I ] >_e.k /

BAt-s+I

~= ~3/2 ->(3e)3

L..~S_I

r BAt_s+1 > (3e)3Lk 3/2

Since any distribution of mi can be obtained from the initial distribution

above by performing the action described above again and again, the lemma

follows. []

Clearly, there are (t+k-1) _< 2t+k-1 possibilities for choosing the ~1,..., ~t

such that ~ti= 1 ~i = k - 1. Thus we get for

BA~ > (3e)3Lk 3/2

for all i that

(~.~-1 t+~_~(13L~t-f'~

P(t,k) <_ n ~, SA 1 ] \~]

n " 2 k t --ff ) t :

For any constant 7 > 0, let

206 12. Protocols for All-Optical Networks

and

(2 + '7) log n

k0 = +1

T >_ (2 + 7) log n + [log ko] 9

If the routing takes more than T rounds then one of the following two cases

must be true:

1. There must exist a valid reduced embedding into a witness tree ]/Y(t)

with t < T and k E {ko,..., 2ko} different worms.

2. There must exist a valid reduced embedding into a witness tree )4;(T)

with k _< ko different worms.

Suppose that Ai > max{16~0~

16L.0 (3e)aLk~/2

, Blogn, B } + D + L. Then we get:

Pr[The routing takes more than T rounds]

_< Pr[Case (1) holds] + Pr[Case (2) holds]

T 2ko ko

<- E E P(t,k) + E P(T,k)

t----log

ko k=ko

k----2

(

T 2ko (1) ~2+~),og.

<_ EEn'2k +

S----log

ko k=ko

ko (~) k-1 1

En. 2k 0

k:2 2e(lo-5~d+log3/2n)+~(v+ 1)

n-- 3, n--" ?"

< -~- + --~- < n-~

Therefore the overall runtime is

E (As + 2(D + L))

t----1

12.5 Proof of Theorem 12.3.2 207

w.h.p., which is bounded by

where a = 6' + B(~ + 1) + 2

and ~ = ~/d

+ 2.

12.5.2 The Lower Bound

In this section we will prove the lower bound in Theorem 12.3.2. We use a

path collection that consists of the following two types of subcollections.

- The first type consists of

n/6

structures consisting of three paths of length

D that are connected as shown in Figure 12.5.

~'"",, path 2

path

I I

Fig. 12.5. A type-1 structure.

I.L/2J edges

- The second type consists of n/(2C) structures each consisting of C identical

paths of length D.

We assume that along each of these paths one worm of length L > 2 has to

be sent. (Note that in case of L = 1 no cycles of colliding worms can occur,

that is, we are in a situation of Main Theorems 12.3.1 and 12.3.3.)

We first compute how long it takes to route all worms in a type-1 structure.

Consider an arbitrary round i of the trial-and-failure protocol. Suppose that

in a given type-1 structure all three worms are still active. Then we want

to calculate the probability that these three worms also block each other in

round i.

Suppose that Ai > L. Let the worm traveling along path j E {1, 2, 3} be

called wj. Let 51 be the delay chosen by worm Wl. In case that 51 _< Ai - [Lj

we get that wl, w2, and w3 collide if w2 and w3 choose the same wavelength

as Wl and delays in the range [51,51 + [Lj _ 1]. In case that (il > Ai -- [~J,

then Wl, w2, and w3 collide if w2 and w3 choose the same wavelength as Wl

208 12. Protocols for All-Optical Networks

and delays in the range [J1 -

(LLJ

- 1),J1]. Hence in both cases there are

at least L L] possibilities for both w2 and wa to choose a wavelength and a

delay such that wl, w2, and w3 collide. Thus the probability that wl, w2,

and w3 collide at round i is at least

(LLJ/(BAi)) 2

if Ali> L. Therefore the

probability that Wl, w2, and w3 collide for t rounds is at least

~1( LL/2J )2

.= \B(Ai +L)

for any choice of A1,...,

> 1. Given a fixed A t

= ~i=l Ai

this product

yields the smallest probability if

Ai = A/t

for all i E {1,...,t}. Hence

assume that all delay ranges are equal to z~ =

A/t.

Since there are

n/6

type-

(

L "~2t

1 structures, and each structure has a probability of at least ~j to

have active worms after t rounds, the expected number of type-1 structures

that have active worms after t rounds is at least

n ( L ) 2t

log(n/6)

6 3B(~--+ L) <1 r t> ( )

log

3B(~L+L)

Hence the expected number of rounds that are needed to route all worms

f2(lOgB(Zl/L+D n).

In order to bound the time needed to route worms in

the type-2 structures, we distinguish between the cases C > 2 l~ and

~ < 2 lox/ffQ-~.

Case C <

2 I~

Note that any routing protocol needs at least/2(~-+ D + L) steps to route all

worms in a type-2 structure. Therefore the expected runtime of the protocol

is at least

(~, + log_~+2 n.

(ZI+D+L))

where a = C +B( D + 1) + 2 and/~ = a/C+ 2.

Case C~ 2 lV/i~n:

This case follows analogous to Section 12.4.

13. Summary and Future Directions

At the end, let us summarize the main results in this book and present

several open problems in the area of store-and-forward and wormhole routing.

Furthermore, we will give an overview on topics that will become increasingly

important in the future.

13.1 Store-and-Forward

Routing

In the following we summarize the most important results that can be found

in the store-and-forward part above and mention some important open prob-

lems. Let us first come back to the questions stated in the introduction. There

we asked

- whether, and for which networks, online protocols can reach the best pos-

sible time of routing arbitrary permutations,

whether, and for which networks, adaptive routing protocols are more ef-

ficient than protocols using oblivious routing strategies,

whether, and for which networks, randomized routing strategies are more

efficient than deterministic routing strategies, and

how space limitations at the processors (such as bounded buffers or limited

space for storing routing tables) influence the routing time.

Concerning the first question, we found out that, given any network of size

N with routing number R at least ~(log

N) for some constant e > 0, the

online protocol by Ostrovsky and Rabani together with the strategies devel-

oped in Chapter 5 yield a protocol that can route any permutation in time

O(R),

w.h.p., which is optimal in the worst case (and average case). For all

bounded degree networks with smaller routing number, replacing the proto-

col by Ostrovsky and Rabani by the duplication protocol yields a protocol

whose runtime deviates by at most a factor of (log log N) 2 from an optimal

runtime of O(R), w.h.p. It is still an open problem, whether also for these

networks a runtime of

O(R)

can be reached.

Concerning the second question, it follows from above that if random

bits are available then for any network with sufficiently large routing num-

ber adaptive routing protocols can not beat protocols using oblivious routing

strategies. This, however, only holds for the worst case (and average case)

210 13. Summary and Future Directions

time of routing arbitrary permutations. We did not address the problem of

reaching the optimal time for any

particular

permutation. The main obstacle

in solving this problem is to construct for any permutation routing problem a

path collection that is (asymptotically) optimal. If random bits are not avail-

able than oblivious protocols behave very poorly (see Theorem 5.2.1). Here

we could show that adaptive protocols can reach much better time bounds

(see Chapter 8). Note that for the case that only a limited randomness is

used to choose paths in a given path system, Krizanc [Kr96] proved a general

time-randomness tradeoff for the congestion of worst case permutations.

Concerning the third question, we could show in Chapter 8 that for any

network with sufficiently large routing number there exists an (asymptoti-

cally) optimal deterministic routing strategy for routing arbitrary permuta-

tions using only constant size buffers. Hence for these networks and routing

problems randomized strategies (asymptotically) can not beat deterministic

strategies. For networks with small routing number this is still an open prob-

lem. Note that even for the butterfly network it is not known so far how fast

deterministic strategies for routing arbitrary permutations can get.

We could also advance in answering the fourth question by presenting

upper bounds in Chapter 9 for the relationship between space for storing

routing information and the slowdown for routing arbitrary permutations in

arbitrary networks.

In the following we summarize our results in more detail and give some

more important open problems in the field of store-and-forward routing.

13.1.1 Path Selection

In Chapter 5 we could show that, for any network of size N with routing

number R -- f2(logN), it is possible to choose online for any permutation

routing problem a path collection with a dilation and congestion of

O(R),

which is asymptotically optimal in the worst case and even in the average

case. However, there are permutations for which there are path collections

with much less congestion and dilation (e.g., the permutation that maps x

to x). Problems also arise if we want to find asymptotically optimal path

collections for arbitrary functions and not only for permutations. Srinivasan

and Teo [ST97] could show that for any routing problem in any network, an

asymptotically optimal path collection can be found in polynomial time. But

it is not known so far whether this can also be done online.

13.1.20ffline

Routing

We have seen that for any simple path collection with congestion C and

dilation D there exists a protocol for routing a packet along each of these

paths in optimal time

O(C + D),

using buffers of size three. An open problem

in this area is whether even for buffers of size one a runtime of

O(C + D)