Сборник докладов - Электроэнергетика глазами молодежи 2010
Подождите немного. Документ загружается.

310
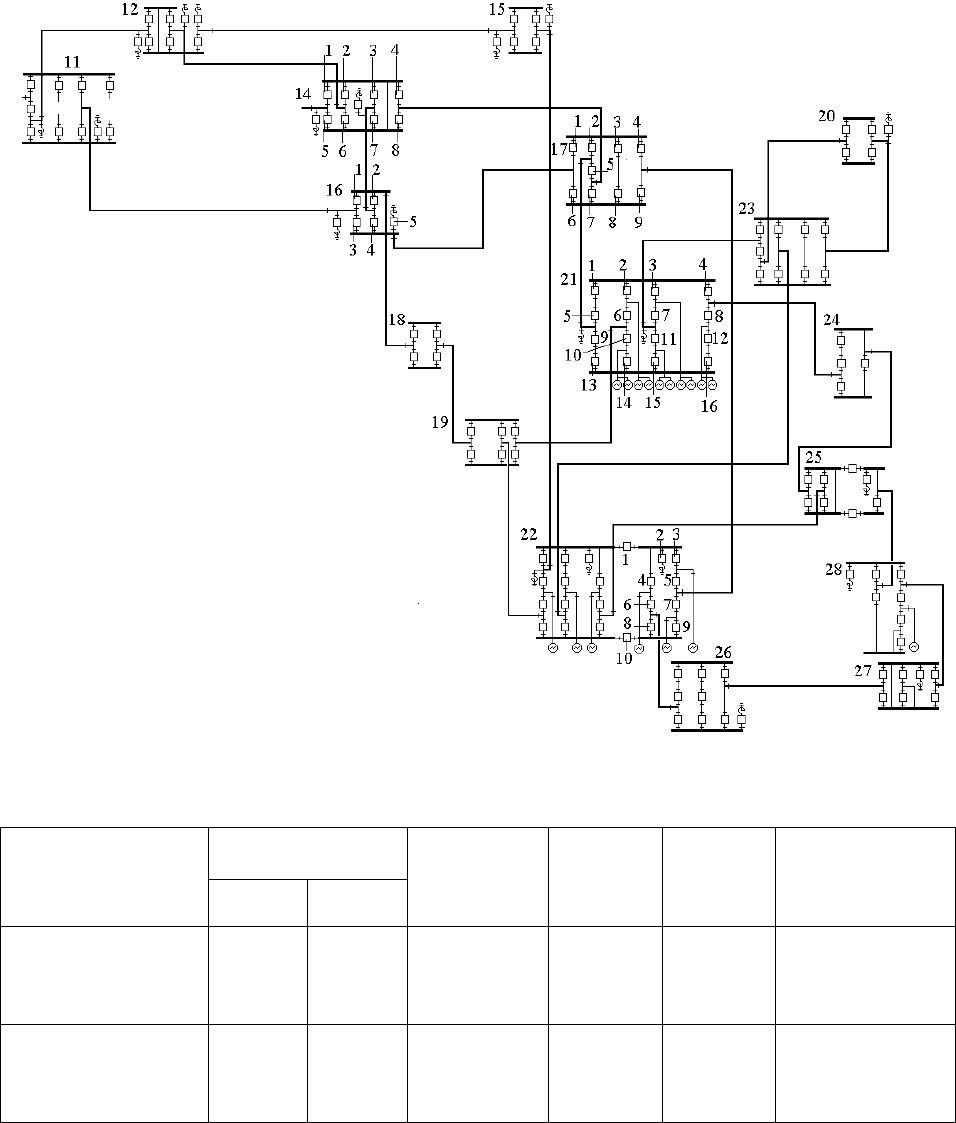
рийном состоянии. Состоянию отказа этого узла соответствует отключение всей нагрузки
соответствующей подстанции.
Рисунок 1 – Исследуемый фрагмент электрической сети
Таблица 1 – Исходные показатели надёжности основного оборудования
Параметр
Воздушные
выключатели
Воздушные
ЛЭП
Разъеди-
нители
Сборные
шины
Блок
электростанции
в цепях
ВЛ
в других
цепях
Частота аварий-
ных отказов,
1/год
0,2 0,08
0,4/0,5
(неуст/уст
на 100 км)
0,04 0,01 2,5
Время аварийно-
го восстановле-
ния, о.е.
0,01 0,01 0,001 0,0004 0,0007 0,05
При расчётах реальных схем объём результирующей информации получается дос-
таточно большим. Так, например, для рассматриваемого фрагмента количество результи-
рующих показателей одного расчёта превышает 250 параметров.
Первый шаг по сокращению объёма результирующей информации – принять ос-
новным показателем частоту отказов наблюдаемых узлов. Данный параметр рассчитыва-
ется программой отдельно для ОТО и ОТКЗ. Для последующего анализа целесообразно
рассчитывать суммарную частоту, характеризующую общее за год число отключений узла
схемы без дифференциации по продолжительности аварийного состояния. Второй шаг –
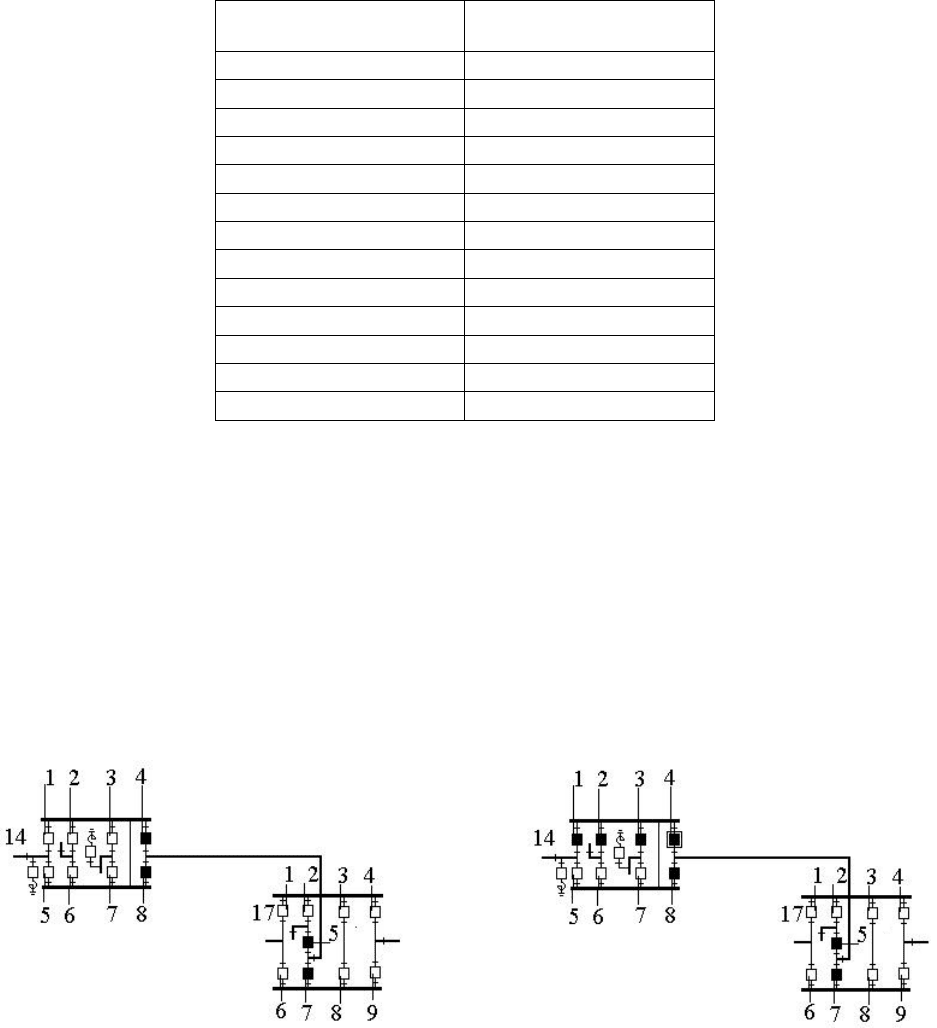
311
использовать данный параметр только для дополнительных узлов, моделирующих полный
отказ распредустройства. И, наконец, суммируя частоту отказов дополнительных узлов с
весами равными мощности нагрузки подстанции в режиме зимнего максимума (таблица 2),
получить оценку годового недоотпуска мощности. Данная величина позволяет интеграль-
но оценить ослабление структуры сети при реализации конкретной ремонтной заявки.
Таблица 2 – Нагрузки подстанций в максимальном режиме
Номер подстанции Нагрузка, МВт
11 224
12 231
14 310
15 282
17 759
18 566
19 1209
20 263
23 944
24 672
25 546
26 530
27 606
Варианты расчётных схем формируются из рассматриваемого фрагмента (рису-
нок 1) в результате поочерёдных отключений линий подстанции № 17. При этом образо-
ваны две группы схем. Первую группу составляют схемы, полученные в предположении
успешного отключения соответствующей линии с обоих концов. Вторую группу образуют
схемы, моделирующие отказ одного из смежных линии выключателей при его отключе-
нии. Более глубокое изменение конфигурации сети моделируется удалением из расчётной
схемы резервирующих выключателей.
Рисунок 2 иллюстрирует принцип формирования вариантов при рассмотрении за-
явки на вывод в ремонт линии «17–14». Вариант а) соответствует успешному отключению
рассматриваемой линии, вариант б) – отказу выключателя № 4 подстанции «14» при от-
ключении линии.
а б
Рисунок 2 – Вариант схемы после успешного (а)
и неуспешного (б) отключения линии
Результаты расчёта схем первой группы представлены в таблице 3, второй группы – в
таблице 4. Для обозначения выключателей указывается номер подстанции и номер вы-
ключателя в распредустройстве. Например, 14-8 – восьмой выключатель подстанции
«Четвёртая».
312
Таблица 3 – Результаты расчёта схем при успешном отключения
линий электропередачи
Вариант
Отключаемая
линия
Успешно отключившиеся
выключатели
Годовая потеря нагрузки
МВт/год %
1 17 – 14 17-5, 17-7, 14-8, 14-4 753 107,12
2 17 – 16 17-1, 17-6, 16-3, 16-4 707 100,63
3 17 – 21 17-2, 17-5, 21-5, 21-9 746 106,05
4 17 – 22 17-4, 17-9, 22-5, 22-7 703 100,00
Таблица 4 – Результаты расчёта схем при неуспешном отключении
линии электропередачи
Вариант
Отключаемая
линия
Отказ
выключателя
Резервирующие
выключатели
Годовая потеря
нагрузки,
МВт/год
1
17 – 14
14-8 14-1, 14-2, 14-3 960
2 14-4 14-5, 14-6, 14-7 960
3 17-5 17-2, 21-5, 21-9 1177
4 17-7 17-6, 17-8, 17-9 1370
5
17 – 16
16-4 16-2, 14-3, 14-7 725
6 16-3 16-1, 11-1, 11-2 1992
7 17-1 17-2, 17-3, 17-4 676
8 17-6 17-7, 17-8, 17-9 676
9
17– 21
17-2 17-1, 17-3, 17-4 1326
10 17-5 17-7, 14-4, 14-8 1188
11 21-5 21-1, 21-2, 21-3, 21-4 787
12 21-9 21-13 745
13
17 – 22
17-4 17-1, 17-2, 17-3 1176
14 17-9 17-6, 17-7, 17-8 1162
15 22-5 22-1, 22-2, 22-3 1172
16 22-7 22-9 1172
Сумма годовой потери мощности по всем неблагоприятным сценариям (таблица 5)
позволяет оценить возможные последствия развития аварии, связанные с реализацией ре-
монтной заявки.
Таблица 5 – Оценка глубины развития аварии
Отключаемая линия
Ожидаемая годовая потеря нагрузки
МВт/год %
17 – 21 4048 100,0
17 – 16 4070 100,5
17 – 14 4466 110,3
17 – 22 4684 115,7
313
Выводы:
1. Разброс итогового критерия в 7 и 15 %, соответственно без учёта и с учетом
возможного отказа выключателей (таблица 3, таблица 5), позволяет дифференцировать
ремонтные заявки по уровню влияния на структуру анализируемого фрагмента электриче-
ской сети.
2. Полученные данные могут быть использованы для выбора стратегии и сокраще-
ния объема последующих режимных расчётов.
3. Для сокращения времени счёта и автоматизации обработки результатов целесо-
образно на основе программы «Струна» разработать специализированный программный
комплекс, адаптированный к решению задач краткосрочного планирования режимов.
Список использованных источников
1. Арзамасцев Д.А. Расчет показателей структурной надежности энергосистем // Д.А. Ар-
замасцев, В.П. Обоскалов: Учебное пособие. Свердловск, изд. УПИ им. С.М.Кирова,
1986, 80 с.
2. Обоскалов В.П. Структурная надежность систем электроснабжения с отказами типа
"короткое замыкание" /Обоскалов В.П., Котов О.М., Дулесов А.С. // Изв. Вузов "Энер-
гетика", 1986, №2. С. 19–23.
3. Обоскалов В.П. Использование метода базисных разрезов для оценки показателей
функциональной и структурной надежности электроэнергетических систем / Обоска-
лов В.П., Кирпикова
И.Л., Котов О.М. // Изв.АН СССР "Энергетика и транспорт", 1989,
№2. С. 27–33.
4. Надежность систем энергетики и их оборудования. Справочник: в 4-х т./Под общ. ред.
Ю.Н.Руденко. Т.2. Надежность электроэнергетических систем. Справочник / Под ред.
М.Н. Розанова. Энергоатомиздат, 2000, 568 с.

314
РАСЧЕТ ПОТЕРЬ
ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ В ЭЛЕКТРИЧЕСКИХ СЕТЯХ
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИМ МЕТОДОМ
А.В. Лыкин, Н.А. Жилина, А.Н. Нестерова
НГТУ
В работе [1] показано, что расчеты потерь электрической энергии могут быть вы-
полнены на основе решения задачи энергораспределения в электрических сетях. При этом
потребление электрической энергии за расчетный период в каждом из узлов расчетной
модели сети считается известным как для активной, так и для реактивной мощности. Рас-
чет баланса активной энергии в сети на основе решения уравнений установившегося ре-
жима сети дает величину нагрузочных потерь, в то время как другие виды потерь элек-
трической энергии должны войти в узловые значения потребления (генерации) энергии
(активной и реактивной). Решение задачи энергораспределения выполняется путем опре-
деления средних потерь активной мощности в сети (математического ожидания потерь
мощности)
за расчетный период . Для этого выражение для расчета потерь мощно-
сти в элементе электрической сети линеаризуется и затем, с учетом напряжения, по чи-
словым характеристикам активной и реактивной мощности, передаваемой по элементу
сети, находится математическое ожидание потерь мощности на расчетном интервале.
Решение задачи энергораспределения более трудоемко в сравнении с расчетом по-
токораспределения в электрической сети. Можно назвать два подхода к расчету энерго-
распределения.
В первом подходе расчетный интервал разбивается на интервалы, для которых
возможно определение потребления мощностей и в узлах сети. Для каждого интерва-
ла находятся потокораспределение и средние значения расчетных потерь и потоков мощ-
ности. Количество переданной и потерянной энергии определяется умножением средних
значений на расчетный интервал . При этом изменением мощностей и на более мел-
ких интервалах времени пренебрегают.
Во втором подходе для активных и реактивных мощностей в узлах сети находятся
функции распределения их значений на полном расчетном интервале
. На их основе на-
ходятся математические ожидания и ковариации (корреляционные моменты) мощностей в
узлах. Далее по уравнениям установившегося режима (УУР) рассчитываются числовые
характеристики напряжений в узлах, потоков и потерь мощности в ветвях сети. Определе-
ние числовых характеристик (математических ожиданий и ковариаций) параметров режи-
ма может быть сделано двумя методами:
методом статистических испытаний (методом Монте-Карло);
прямым расчетом числовых характеристик по линейным и квадратичным зави-
симостям (методом статистической линеаризации).
Первый подход требует почасовых (или более частых) измерений всех мощностей
потребления и генерации в узлах сети, что, в настоящее время, далеко не всегда возможно.
Фактически расчет происходит в темпе процесса на основе данных АИИС КУЭ (АСКУЭ).
Второй подход использует обобщенную информацию о потреблении энергии:
интервал изменения активных и реактивных мощностей в каждом узле сети;
вид (функцию) закона распределения мощностей в каждом узле сети;
величины коэффициентов корреляции между активными и реактивными мощ-
ностями для каждого узла и для каждой
пары узлов.
315
В идеальном случае, при наличии измерений мощностей потребления (генерации) в
узлах, рассчитываются их статистические числовые характеристики.
В настоящей статье излагаются некоторые аспекты второго подхода к определению
числовых характеристик параметров режима сети и потерь электрической энергии.
Метод расчета заключается в вычислении средних за расчетный период потерь
мощности в электрической сети. Расчет состоит в решении системы УУР при представле-
нии мощностей нагрузок узлов случайными величинами. Такая модель предполагает, что
все изменения мощностей, как регулярные (циклические суточные, недельные и годовые),
так и нерегулярные (вызванные другими внешними факторами, в том числе и случайны-
ми), описываются как случайные. Законы распределения мощностей отражают их упоря-
доченную вариацию в расчетном периоде, а числовые характеристики определяются ос-
реднением по времени единственной реализации – графика нагрузки на расчетном интер-
вале. Необходимо преобразовать одну систему случайных величин – мощности в узлах, в
другую систему – напряжения в узлах сети, и затем по ним вычислить математическое
ожидание потерь мощности. По сути, знание вида закона распределения мощностей и на-
пряжений в узлах сети в этой постановке задачи не нужно, необходимы лишь их числовые
характеристики – математические ожидания и ковариационные моменты. Поэтому реша-
ется частная задача – преобразование числовых характеристик систем случайных величин.
Система УУР является нелинейной, и нахождение числовых характеристик напря-
жений в узлах можно выполнить лишь приближенно. Используя форму записи УУР в де-
картовых координатах, которая содержит только мультипликативную нелинейность, мож-
но получить точное уравнение, связывающее математические ожидания и ковариации
мощностей и напряжений в узлах сети. Однако и в этом случае возникает погрешность,
которая образуется в соотношениях моментов распределения второго порядка – ковариа-
ций, так как для определения ковариаций напряжений в узлах сети приходится прибегнуть
к линеаризации УУР, что собственно уже делается при их решении методом Ньютона.
В общем виде математическая модель установившегося режима электрической се-
ти, состоящей из n узлов, для числовых характеристик мощностей (исходные данные) и
напряжений в узлах (искомые величины) записывается в виде [2]:
cov
,
cov
,
cov
,
cov
,
,
cov
,
cov
,
cov
,
cov
,
,
(1)
где
и
– математические ожидания мощностей в узлах сети;
и
– элемен-
ты матрицы узловых проводимостей (активная и реактивная составляющие);
,
,
,
– математические ожидания вещественной и мнимой составляющих комплек-
сов напряжений в узлах; cov
,
,
,
, cov
,
, cov
,
– ковариации меж-
ду составляющими напряжений в узлах и j, и
cov
,
cov
,
, (2)
где – матрица Якоби системы уравнений (1); cov
,
– ковариационная матрица со-
ставляющих комплексов напряжений в узлах; cov
,
– ковариационная матрица мощ-
ностей в узлах.
316
После совместного решения систем уравнений (1) и (2) определяется математиче-
ское ожидание потерь мощности
∆
2 cov
,
2 cov
,
, (3)
где и – номера узлов, примыкающих к ветви .
Потери электрической энергии есть среднее значение потерь, умноженное на рас-
четный интервал времени T
р
,
∆
∆
р
. (4)
Рассматриваемый метод расчета потерь электрической энергии имеет следующие
особенности:
1) требуется построение особой математической модели нагрузок узлов – матема-
тических ожиданий и ковариационной матрицы мощностей в узлах (см. ниже);
2) расчет связан с решением довольно большой системы уравнений;
3) необходимо учитывать корреляционные связи между мощностями всех нагрузок
электрической сети;
4) расчет возможен для любого расчетного интервала – от нескольких минут до го-
да – и учитывает реверсивность потоков мощности в ветвях сети на расчетном интервале,
что дает возможность расчета потерь электрической энергии в сложнозамкнутых электри-
ческих сетях.
В целом по электрической сети режим энергопотребления на некотором расчетном
интервале времени описывается совокупностью графиков нагрузки по активной и реак-
тивной мощности. При интервале дискретизации от нескольких минут до одного часа та-
кие графики являются исчерпывающей характеристикой режима потребления. При отсут-
ствии регулярных измерений мощности в реальном времени приходится пользоваться ин-
тегральными измерениями – энергией, что приводит к потере собственной и взаимной за-
висимостей потребляемых мощностей во времени. В этом случае можно использовать ве-
роятностно-статистическую модель энергопотребления (ВСМЭ).
Основная идея построения ВСМЭ заключается в оценке математических ожиданий
мощностей в узлах по измерениям активной и реактивной энергии, а корреляционные мо-
менты второго порядка (ковариации) определяются по оценкам интервалов изменения
мощностей и корреляций, полученных из наблюдений разных лет, аналогичных потреби-
телей, суточных и сезонных изменений и пр. Кроме этого, возможно проведение дополни-
тельных исследований доступного статистического материала с целью выявления общих
закономерностей, влияющих на моменты распределения второго порядка. При этом ва-
риация мощностей на расчетном интервале принимается случайной.
При формировании ВСМЭ определение средних мощностей нагрузок на расчетном
интервале времени обычно не вызывает затруднений – количество потребленной в узле
нагрузки электроэнергии делится на расчетный период. При наличии реверсивного пере-
тока электроэнергии в узле нагрузки берется сальдированная величина. Основная труд-
ность заключается в формировании матрицы ковариаций мощностей нагрузок.
Дисперсии мощностей следует определять по длине интервала изменения мощно-
сти нагрузки. Для этого необходимы крайние значения мощности на этом интервале – ми-
нимальное и максимальное значения. Кроме того, необходимы хотя бы ориентировочные
данные о виде закона распределения мощности нагрузки. Тогда, например, для активной
мощности при симметричном законе распределения среднеквадратическое отклонение
(СКО) можно вычислить по формуле

317
σ
max
min
2
, (5)
где
max
,
min
– максимальная и минимальная активная мощность на расчетном интервале;
– коэффициент, определяющий длину интервала распределения случайной величины
(коэффициент кратности σ
).
Значение зависит от вида закона распределения. Так, при равномерном распреде-
лении t
√
3, а для законов с бесконечным интервалом распределения его получают по
заданной доверительной вероятности попадания в ограниченный интервал распределения.
Для оценки величины t были рассчитаны значения СКО для суточных, месячных и
годовых графиков суммарной активной нагрузки одной из энергосистем. Для суточных и
месячных графиков средняя оценка t оказалась равной 1,95, а для года 2,3.
Анализ ряда типовых графиков разных видов нагрузки и данных реальных измере-
ний потребления активных и реактивных мощностей нескольких потребителей, получен-
ных по данным АИИС КУЭ, позволяет отметить некоторые общие свойства нагрузок рас-
пределительных электрических сетей на суточном интервале:
1) для большинства нагрузок минимальное значение мощности нагрузки достаточ-
но сильно отличается от нуля;
2) распределение мощностей близко к симметричному закону относительно центра
распределения;
3) корреляция между мощностями одной нагрузки и между разными нагрузками
может быть достаточно велика, подсчитанные значения коэффициента корреляции мощ-
ностей на суточном интервале изменяются от 0,36 до 0,98. Отрицательная корреляция или
отсутствие корреляции не характерны для всех графиков нагрузки.
Основное влияние на коэффициент корреляции графиков нагрузки узлов сети ока-
зывают циклические изменения, обусловленные суточным и недельным ритмом жизни
людей и сезонными изменениями электропотребления в течение года. Промышленные на-
грузки, как правило, имеют особенности из-за разной сменности работы производств и, в
отдельных случаях, сезонных работ.
Для преимущественно бытовой нагрузки с небольшой долей промышленных по-
требителей были рассчитаны коэффициенты корреляции активных и реактивных мощно-
стей нескольких узлов для суточного графика нагрузки. Наибольшая корреляция отмеча-
ется между активными мощностями фидеров 0,88–0,96, корреляция между активными и
реактивными мощностями одной нагрузки изменяется в пределах 0,62–0,92, самая низкая
корреляция оказалась между реактивными мощностями узлов – 0,33–0,73.
Приведем результаты расчета потерь электрической энергии на одном примере.
Аналогичный пример для оценки точности расчета потерь электрической энергии для ме-
тодов времени наибольших потерь и средних нагрузок рассмотрен в [3].
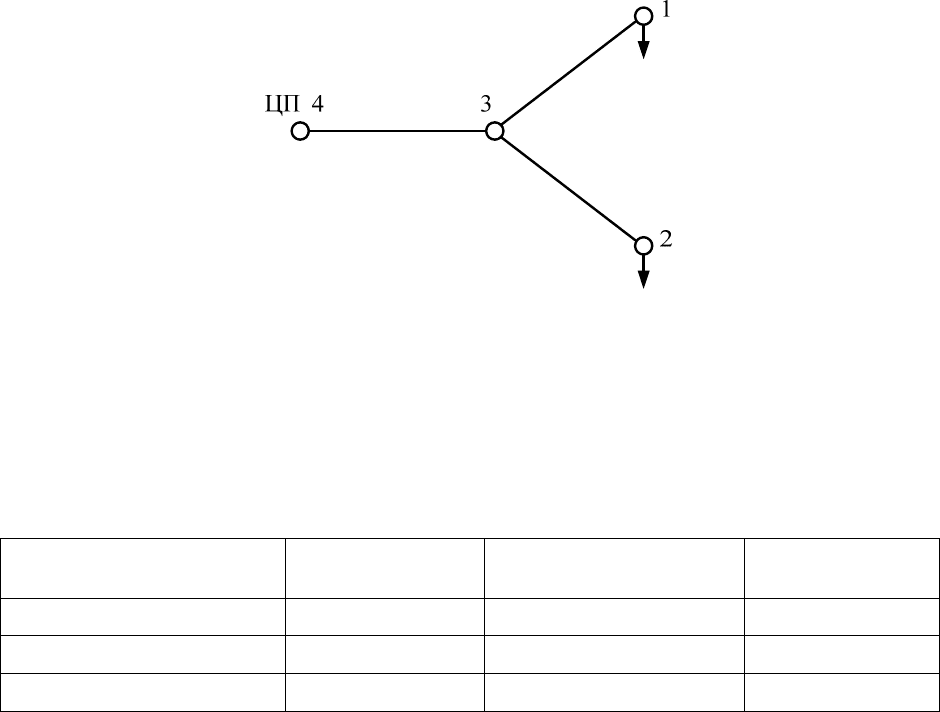
В схеме электрической сети, изображенной на рисунке, рассчитываются потери
электрической энергии за сутки. Схема состоит из трех ЛЭП напряжением 110 кВ, выпол-
ненных проводом АС-70/11. Каждая линия имеет две цепи и длину 40 км. Схема имеет два
узла с разнородными нагрузками. Средние мощности нагрузок (в МВ·А) за сутки:
16,7 6,7;
20,5 8,6,
а СКО:
σ
9,0 3,6; σ
11,4 4,8.
318
Рисунок – Схема электрической сети 110 кВ
За эталонный метод был принят расчет по часовым значениям графиков нагрузки P
и Q узлов 1 и 2. Расчеты были выполнены вероятностно статистическим методом и мето-
дом средних нагрузок, для которого коэффициент формы графика нагрузки был рассчитан
по графику головного участка сети. Результаты расчета средних потерь мощности, потерь
электроэнергии и погрешности результатов приведены в таблице.
Таблица – Результаты расчета потерь электроэнергии по разным методам
Метод расчета
Средние потери
мощности, МВт
Потери электрической
энергии, тыс. кВт·ч
Погрешность
расчета, %
Эталонный расчет 2,019 48456 –
Метод средних нагрузок 1,852 44448 –8,27
ВСМЭ 2,027 48648 0,40
Выводы. Наряду с известными методами расчета потерь электрической энергии
для задач анализа и повышения экономичности работы существующих, а также проекти-
руемых электрических сетей, можно использовать метод, основанный на вероятностно-
статистической модели режима энергопотребления и аппарата преобразования числовых
характеристик случайных величин. При корректном представлении режима энергопотреб-
ления электрических нагрузок этот метод дает
наиболее точные результаты расчета по-
терь электроэнергии.
Список использованных источников
1. Паздерин А.В. Расчет технических потерь электроэнергии на основе решения задачи
энергораспределения // Электрические станции, 2004. № 12. С. 44–49.
2. Лыкин А.В., Тутундаев М.Л. Расчет потерь электрической энергии на учетных интерва-
лах при наличии реверсивных перетоков мощностей // Научные проблемы транспорта
Сибири
и Дальнего Востока. Специальный выпуск № 1. 2009. С. 65–69.
3. Железко Ю.С. Потери электроэнергии. Реактивная мощность. Качество электроэнергии:
Руководство для практических расчетов. М.: ЭНАС, 2009. 456 с.

319
РАСЧЕТ ПРЕДЕЛЬНЫХ РЕЖИМОВ
КОМБИНИРОВАННЫМ МЕТОДОМ НЬЮТОНА
А.В. Паздерин, С.В. Юферев, В.С. Никифоров
УрФУ
Расчет установившихся режимов (УР) является базой, на основе которой решаются
другие, более сложные, задачи управления функционированием и развитием электроэнер-
гетических систем (ЭЭС). Основная проблема расчета УР – существование решения и
сходимость итерационного процесса. Отсутствие сходимости обычно означает, что режим
неустойчив и на практике не может быть реализован. Разработка методов и алгоритмов
расчета УР, обеспечивающих надежную сходимость к решению, по-прежнему актуальна,
что также связано с желанием гарантированного получения решения, которое находилось
бы на границе области существования, в ситуации, когда исходные данные являются не-
совместными и требуется ввод режима в область существования и в допустимую область.
Все более актуальными становятся задачи, связанные с расчетом предельных режимов и
оценкой запасов статической устойчивости в цикле оперативного управления ЭС. В рабо-
те представлен метод для расчета режимов ЭЭС, которые лежат вне области существова-
ния решения для метода Ньютона-Рафсона (Н-Р).
Систему уравнений УР в общем виде можно записать как:
,
0, (1)
где
– вектор заданных для расчета параметров режима. При расчете УР в каждом узле,
кроме балансирующего, задается либо активная и реактивная мощность, либо активная
мощность и модуль напряжения.
,
– нелинейная вектор-функция. Переменные
определяют условно-постоянные параметры, связанные со схемой замещения электриче-
ской сети. Вектор – искомый вектор состояния, определяющий режим работы ЭЭС, его
размерность совпадает с числом нелинейных уравнений системы (1).
Известны различные формы записи уравнений УР. Обычно это уравнения узловых
напряжений в форме баланса или мощностей или токов. Комплексные величины в этих
уравнениях могут представляться в полярной или прямоугольной системе координат, что
приводит к достаточно большому многообразию форм
записи уравнений УР.
В предлагаемом способе решения задача расчета УР связана с поиском нулевого
минимума целевой функции суммы квадратов невязок [1]:
,
,
. (2)
Уравнения УР ЭЭС при определенных значениях параметров сети и режима могут
оказаться несовместными. В случае, когда исходные данные несовместны, то есть не су-
ществует решения с нулевыми невязками, использование целевой функции может позво-
лить получить приближенное решение с наименьшим несоответствием между расчетными
и заданными узловыми мощностями. Такое решение интересно тем, что позволяет оценить,
насколько заданный вектор исходных данных выходит за границы области существования
решения. Ненулевые невязки узловых мощностей можно рассматривать в качестве управ-
ляющих воздействий для перевода режима на границу области существования режима.
Минимум функции (2) достигается в точке, где производные по всем искомым пе-
ременным равны нулю:
2
,
. (3)
